Parameter optimization for a vibration attenuation system on ambulance stretchers

2.1. Vibration model

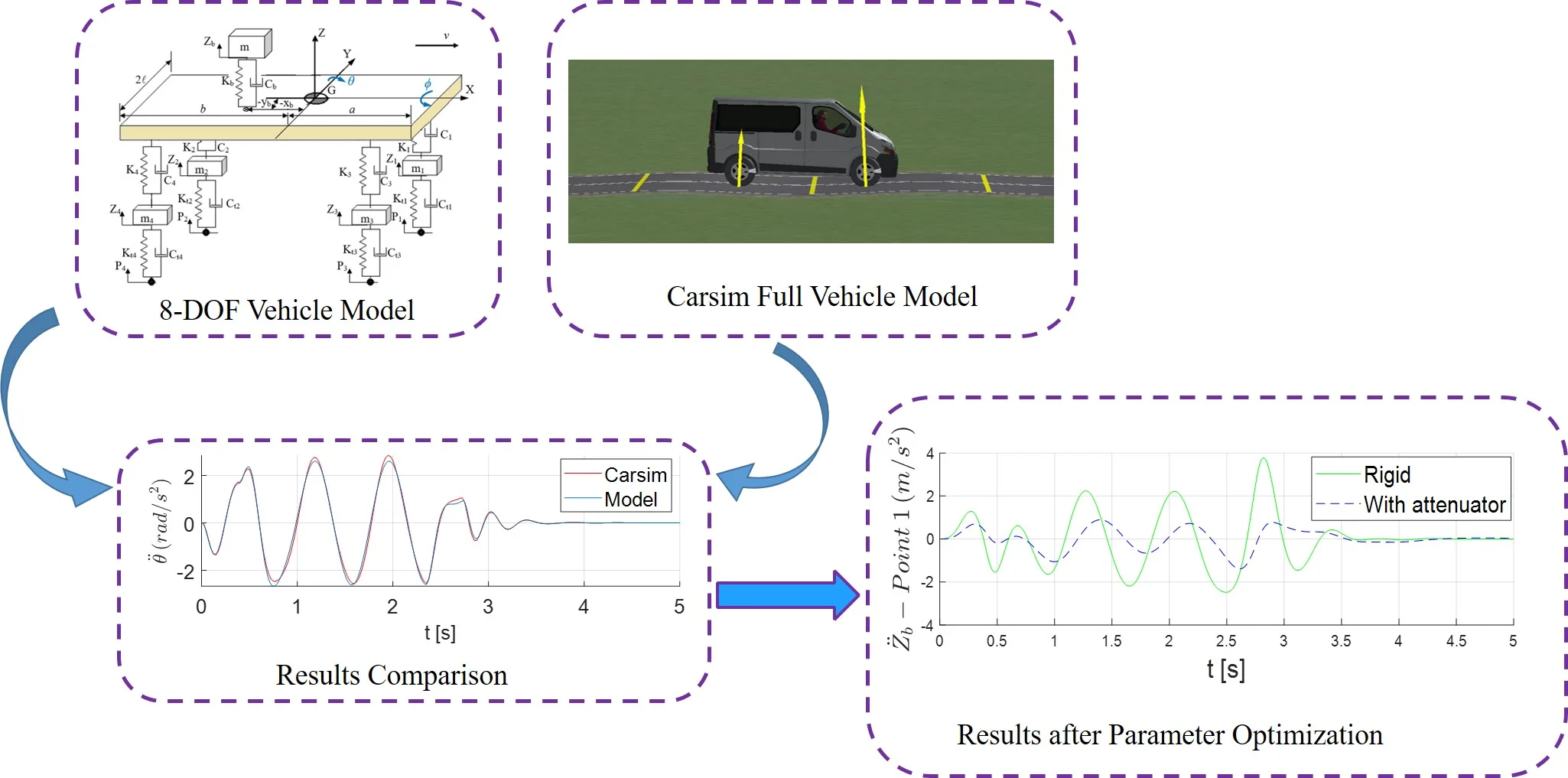
Fig. 1(a) shows the 8-DOF of the dynamic model of a vehicle, which are the vertical displacements of the stretcher and of the vehicle mass center, roll and pitch angles of sprung mass, and the vertical displacement of each wheel. The independent wheel suspension, the tire and the vibration attenuation system under the stretcher are modeled by linear springs with dampers. In the dynamic analysis the vehicle behavior was simulated driving over a sinusoidal road profile with a speed of 30 km/h. A sinusoidal shape of the road profile consists of three successive bumps of height equal to 0.1 meters and total length of 19.5 m [9]. This road input introduces bounce and pitch motion of the vehicle sprung mass simultaneously, as illustrated in Fig. 1(c).

Fig. 1a) 8-DOF vehicle dynamic model; b) locations of points 1 and 2 and vehicle’s mass center G [5]; c) sinusoidal road profile

a)

b)

c)

The equations of motion for the system presented in Fig. 1 are derived according to the Lagrangian formalism:

In this equation, $L=T–V$ is the Lagrangian of the system, and each $q$ represents a generalized coordinate of the system. The corresponding expressions for the kinetic ($T$) and potential ($V$) energies, and for the Rayleigh dissipation function ($R$) are shown in Appendix.

The differential equations of motion are represented in matrix form, as follows:

where $\mathbf{q}={\left[Z_{b}Z\varphi \theta Z_1{Z}_2{Z}_3{Z}_4\right]}^T$ is the column-vector of generalized coordinates.

The Dormand-Prince Runge-Kutta method (DOPRI54) is applied for numerical integration. The initial position (starting point) of all variables and their first time derivative are zero.

The natural frequencies of the system were calculated by solving the associated eigenvalue problem:

where $\omega$ stand for the natural frequencies of the system.

2.2. Vehicle parameters

The ambulance parameters applied to the simulations (Table 1) are compatible with Mercedes-Benz's Sprinter 415 CDI 7.5 m³ vehicle adapted to the ICU model, widely used for patients transport in Brazil, while Fig. 1(b) illustrates the corresponding ambulance parameters.

2.3. Parameter optimization and analysis

In order to achieve a good performance in terms of the ride comfort of the passenger, engineers usually point out improvements in the design of vehicle suspension. However, in Brazil, ambulances usually are adapted from cargo transport vehicles which do not have a customizable suspension. Because of that, ride comfort may not be suitable for patients, and it could aggravate their clinical condition during their transportation.

In view of the above, the authors of this article have been developing a system whose purpose is to attenuate vibrations on ambulance stretchers. In this study, a parameter optimization method is applied to determine the damping and stiffness coefficients of this system that could minimize the vertical acceleration of the stretcher. According to Baumal [9], ride comfort is improved when the magnitude of vertical acceleration is reduced. So, the objective function of the optimization problem is designed to minimize the vertical acceleration experienced by the patient. The point chosen to calculate the acceleration, denoted as point “2” in Fig. 1(b), represents the abdominal region, defined based on the anthropometric dimensions of a medium stature person [12].

As constraints to the optimization problem, the maximum allowable jerk experienced by the patient (${\max \stackrel{⃛}{Z}}_b=$ 18 m/s³) is chosen in accordance with [13], and the workspace of the vibration attenuation system is limited according to the following inequality:

In view of the above, the optimization problem was formulated as follows:

– Minimize ${\ddot{Z}}_b(K_b,\mathrm{}{C}_b)$.

– Subject to $\left\{\begin{array}{c}\begin{array}{l}2000\le K_b\le 30000,\\ 5\le C_b\le 500,\\ \left|Z_b-Z+\theta X_b\right|-0.08\le 0,\\ {\stackrel{⃛}{Z}}_b\le 18\mathrm{}m/s^3.\end{array}\end{array}\right.$

This constrained optimization problem was solved by applying the square quadratic programming (SQP), implemented in MATLAB software, using the built-in fmincon function.

3.1. Comparison between the results obtained by the model and Carsim software

Results of the vehicle dynamic simulations demonstrate responses to displacements and acceleration of the ambulance which rides the Sinusoidal Road Profile described in Section 2.1. First, the results obtained by the 8-DOF model are compared to the corresponding ones obtained from a simulation in Carsim adopting the same parameters, inputs and initial conditions. Fig. 2(a) and 2(b) show the displacement of the mass center of the vehicle ($G$), and the vertical acceleration of $G$, respectively. The time series of vertical acceleration of points 1 and 2 are illustrated in Fig. 2(c) and 2(d). In this simulation scenario the accelerations of these points of the stretcher were computed in the absence of a patient. The corresponding pitch angle and pitch acceleration of sprung mass, in turn, are shown in Fig. 2(e) and 2(f). The results in Fig. 2 clearly show the adherence between the results obtained from the proposed model and the ones from Carsim software.

Fig. 2Time series of displacements and accelerations: a) displacement of vehicle center of mass G; b) vertical acceleration of vehicle center of mass G; c)-d) vertical acceleration of points 1 and 2, respectively; e) pitch angle of sprung mass; f) pitch acceleration of sprung mass

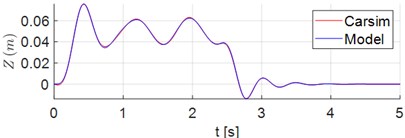
a)

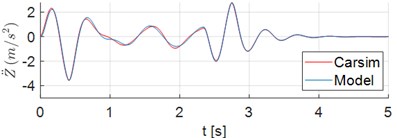
b)

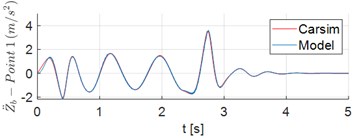
c)

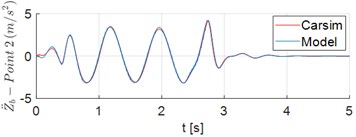
d)

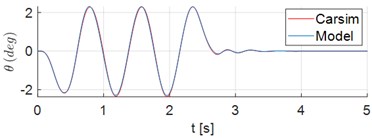
e)

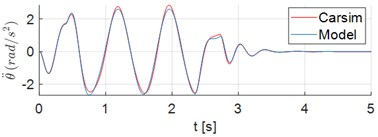
f)

3.2. Parametric optimization analysis

As previously mentioned, the goal of this study is to determine the damping and stiffness coefficients of a vibration attenuation system to be designed for mounting a stretcher in an ambulance, which may be capable to minimize the magnitude of the corresponding vertical acceleration of this stretcher.

Table 2 lists the results obtained from the choice of five independent starting points for the parametric optimization algorithm. It can be observed that the minimum vertical acceleration of stretcher, measured in point 2 $\left({\ddot{Z}}_b\right)\text{,}$ see Fig. 1(b), was achieved with the parameters $K_b$ = 2000 N/m and $C_b$ = 349.7 Ns/m. Additionally, all the constraints of the problem are satisfied. In Table 2, ${\omega }_1$ represents 1st natural frequency, associated to $Z_b$ movement.

Fig. 3 shows the time series of accelerations of points 1 and 2 when the ambulance rides the Sinusoidal Road Profile described in Section 2.1. The patient plus stretcher mass adopted in the simulation is equal to 120 kg.

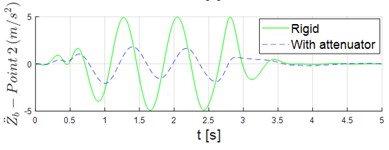
The vibration attenuation system is capable of significantly reducing the vertical acceleration in both the head (point 1) and stomach region (point 2) of patient as shown in Fig. 3. The peaks of acceleration at Points 1 and 2 were reduced in 63.1 % and 58.4 %, respectively. In addition, the peaks of stretcher jerk (${\stackrel{⃛}{Z}}_b$) at points 1 and 2 points decreased from 35.08 m/s³ to 13.87 m/s³ and from 40.94 m/s³ to 16.63 m/s³, respectively.

Fig. 3Time series of vertical acceleration stretcher when it is rigidly mounted vs. when the attenuation system is used: a) point 1; b) point 2

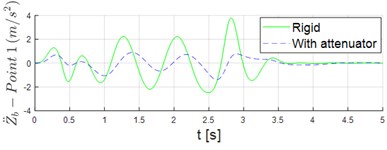
a)

b)