Dynamical analysis and validation of motion control by filtering performance for aerial robotic system

1. Introduction

The research of quadcopters has become an attractive topic in industrial applications and monitoring fields due to their quick development and easy execution [1]. It is stated that this system still plays a crucial role for investigators in many years. In [2], inspectors were considered to use a quadrotor as one of the important methods to verify the transportation infrastructures such as a tunnel or a bridge. This research emphases on innovating the position control without using the global positioning system (GPS) and offers a solution for detecting a tethered quadrotor's airframe location from the length and tension or force of the tether.

The problem of state estimation becomes one of the popular topics in the aerial vehicle system. Commonly, many researchers chose the filtering approach to give a solution for these problems. However, various filter technologies have been utilized to estimate the system state of aerial vehicle. Several enhanced filters, for example, particle filters, are difficult to be computed and have a high cost of labor. It requires a powerful microprocessor to be managed in the control board. Reversely, some filters, for instance Kalman filter and Complementary filter, reveal the effectiveness and are popular because of their frequency filtering performance in the linearization system [3]. Dissimilar studies developed the Kalman filter [4] in the flight control subject. To estimate the system state at specific attitude or hovering the air vehicle, authors [5] adjusted the typical Kalman filter to enhance the adaptive response. The output values are computed by using a multiple extended Kalman filter. The state observer obtains data from different sensors such as accelerometers, gyroscopes and GPS. The study in [6] introduced an unscented Kalman filter by using the three-axes attitude identification scheme as the system observer. It operates resourcefully, but needs computational capability considerably. Additionally, this approach is also useful to trace the motion [7-9]. The desired filtering data is provided from a small inertial/magnetic sensor. As well, the extended Kalman filter is proper for an uncertain system which contains the nonlinear components. It could be embedded into a pixhawk module that satisfies the further optimization operation of the attitude detection [10]. The px4 or pixhawk module is also combined with an open-source platform, for example gazebo, to develop the hardware-in-the-loop [11].

On the other hand, a method of filter techniques is to integrate a Complementary filter [10] which has little computational complexity in the aerial vehicle system. Owing to the simple framework and high efficiency, many investigators and developers are concerned to research the attitude estimation. In [11, 12], researchers indicated that the high-order linear model of Complementary filter is globally asymptotically stable. Two kinds of filter, named as direct and passive, are completed as the work presented in [3]. Moreover, the proposed design is perfectly deterministic while it is based on the linear Complementary filter. This work is considered as the deterministic attitude estimation algorithm.

Kalman filter and Complementary filter are implemented correspondingly in the model of quadcopter to achieve the response in this work. The key contribution is to launch the performance of each filter in quadrotor to prove in which case it can be valuable. The rest of this article is structured as follows. Section 2 briefly reviews the previous works and describes the theoretical principles to estimate the orientation and acceleration in the real-world applications [12]. In Section 3, the mathematical models of both Kalman filter and Complementary filter are depicted basically. Sequentially, the motion analysis of aerial vehicle are demonstrated in Section 4. The theoretical results in Section 5 are simulated to visualize the effective design. Then, several experiments in Section 6 are established to verify our contributions. In Section 7, the conclusions are presented.

2. Investigation of theoretical principle

3. Mathematical model of filters

3.1. Complementary filter design

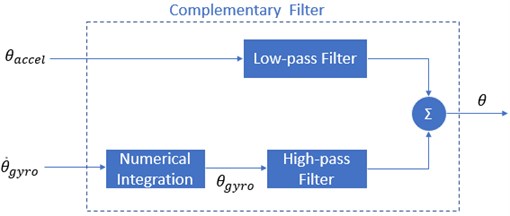
To overcome the drifted problem in the gyroscope and to lessen high-frequency noise from an accelerometer, a Complementary filter is recommended to evaluate angles ${\theta }_{estimate}$ based on the variation of speed ${\dot{\theta }}_{gyro}$ from a gyroscope. Later, it is added with angles ${\theta }_{accelerometer}$ from the accelerometer as Fig. 1(a). It is considered to have small values, and the estimation of roll value $\mathrm{\Phi }$ and pitch value $\theta$ are known, respectively:

13

$\theta \left(n\right)=\gamma {\theta }_{estimate}\left(n\right)+\left(1-\gamma \right){\theta }_{accelerometer}\left(n\right),\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}0.5\le \gamma \le 1.$

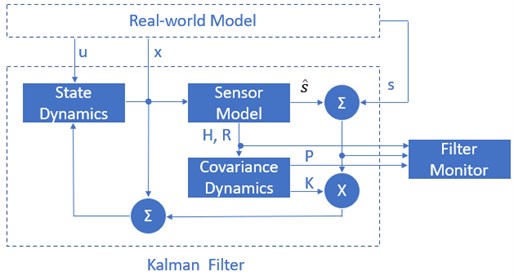
Fig. 1Structure of a) Complementary Filter and b) Kalman Filter

a)

b)

The superiority of the Complementary filter mainly concentrates on the parameter $\gamma$. In this filter, a delay time happens in the output signal (regularly because of the low-pass filter of accelerometer and high-pass filter from gyroscope). The more $\gamma$ value is near to 1, the better quality this filter has. However, the estimation of the sensor readings, which are varied fastly, takes a longer convergent time. It requires to take much effort to estimate the yaw angle directly from an accelerometer, so presently, we still apply values inferred from a gyroscope and accept the drifted phenomenon. By using more magnetic sensors, this problem will be solved.

4. Motion analysis for aerial vehicle

It is considered that Quadcopter is a solid object to be abided by forces such as the total force of motors and moments. In Fig. 2, a model of a quadrotor is analyzed. Each motor produces a force $T_i$ to lift up and a moment $M_i$ to turn the Quadcopter. The gravitational force is usually located at the origin and is directed towards the center of the earth.

Fig. 2Modeling analysis for aerial vehicle

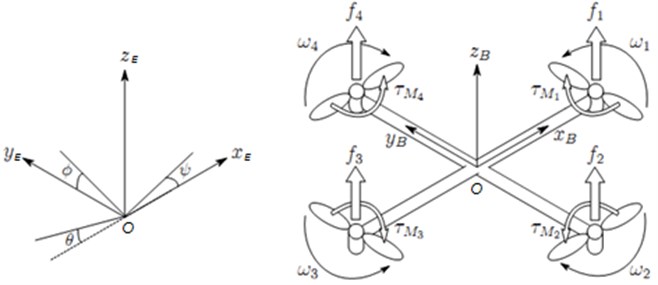
$\left\{E\right\}=\left[x_E,y_E,z_E\right]$, $\left\{B\right\}=\left[x_B,y_B,z_B\right]$ and $\left\{C{S}_v\right\}=\left[x_v,y_v,z_v\right]$are the inertial coordinate, body coordinate, and vehicle coordinate, respectively. $x,y,z$ which are frames in the centroid of quadcopter model, correspond $x_E,y_E,z_E$ axes in the frame system $\left\{E\right\}$ and $x_B,y_B,z_B$ axes in the frame system $\left\{B\right\}$.

Matrix $R_B^E$: is the rotation matrix from frame $\left\{B\right\}$ to frame $\left\{E\right\}$:

Matrix $R_E^B$: is the rotation matrix from frame $\left\{E\right\}$ to frame $\left\{B\right\}$:

Position vector ${\xi }^E$ in frame $\left\{E\right\}$ and linear velocity vector $V^B$in frame $\left\{B\right\}$ are related as follows:

Matrix $T$ is defined to perform the relationship between the angular velocity vector $v^B$ in frame $\left\{B\right\}$ and frame $\left\{E\right\}$:

Using the Newton’s 2nd rule to the translational motion, the dynamic equation of system is analyzed [19]:

where $V^B={\left(u,v,w\right)}^T$, ${\omega }^B={\left(p,q,r\right)}^T$ and applied torque $\tau ={\left[\begin{array}{lll}{\tau }_{\varphi }& {\tau }_{\theta }& {\tau }_{\psi }\end{array}\right]}^T$.

From the Newton’s 2nd rule to rotational motion, the following can be gotten:

Assume that aerial vehicle has symmetric architecture and axes in $\left\{B\right\}$ coordinate are the same with inertial axes of Quadcopter:

Generally, the gravitational force $F_g^E$ is determined as $F_g^E=m{\left[\begin{array}{lll}0& 0& g\end{array}\right]}^T$. Similarly, we can have gravitational force $F_g^B$in frame $\left\{B\right\}$ as $F_g^B=R_E^B\text{,}$$F_g^E=mg{\left[\begin{array}{lll}-\mathrm{s}\mathrm{i}\mathrm{n}\theta & \mathrm{s}\mathrm{i}\mathrm{n}\varphi \mathrm{c}\mathrm{o}\mathrm{s}\theta & \mathrm{c}\mathrm{o}\mathrm{s}\varphi \mathrm{c}\mathrm{o}\mathrm{s}\theta \end{array}\right]}^T$.

The quadrotor suffers forces $f_i$ from 4 Brushless DC (BLDC) motor to form total upward thrust force $F_f^B$ in frame $\left\{B\right\}$ as $F_f^B={\left[\begin{array}{lll}0& 0& -f\end{array}\right]}^T$ with $b$ as the thrust factor:

Therefore, the total force that acts on Quadcopter is summarized:

Then, torque value is achieved by applying the Newton’s 2nd rule to rotational motion:

where $L=J{\omega }_b$ is the angular moment. The Coriolis equation is applied to evaluate the time derivative of the angular moment in the body coordinate.

From Eq. (23), the torque that demonstrates a model of the quadrotor is specified as follows:

The length from $O_b$ to BLDC motor, d is a drag element, and ${\mathrm{\Omega }}_1,{\mathrm{\Omega }}_2,{\mathrm{\Omega }}_3,{\mathrm{\Omega }}_4$ are angular velocities of motor 1, motor 2, motor 3, and motor 4, respectively.

To unify, the total force is applied to frame $\left\{E\right\}$ as follows:

Later, from Eq. (21), the linear and angular accelerations are formed:

where $U_1,U_2,U_3,U_4$ are control signals:

There is air resistance, which affects the quadrotor in the outside environment. Thus, the air drag force can be counted as:

where $C_d$, $\rho$, $S$ and $v$ are drag coefficient, the mass density of the air flow, reference area of the object, and the object’s speed relative to the air flow correspondingly. In reality, the actual speed endures the limited barriers that cannot be overcome as follows:

5. Results of numerical simulation

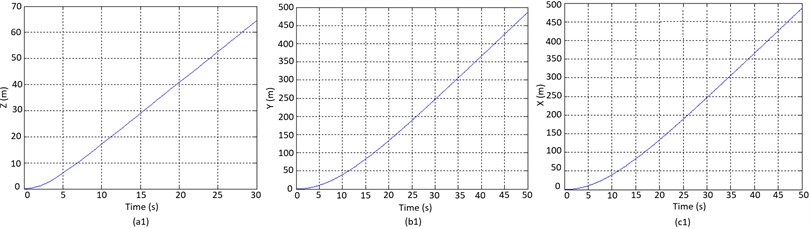
In this section, all simulations are verified with parameters as in Table 2. In the Complementary filter, $\gamma$ varies from 0.96 to 0.98. Also, $R$ is 0.6~0.8 for Kalman filter. The motion of the Quadcopter in the z-axis is illustrated as follows:

To track the motion on the $z$-axis, the roll angle and pitch angle must equalize to zero. The force which is provided by each motor is computed as $F_{balance}=$3, 2.9, 81/4 = 7,848 N. Hence, a force to lift up must be larger than $F_{balance}$. In this case, $F=$4.8 = 32 N is chosen. This force should be smaller than $F_{limit}=$ 50 N in each motor. The simulation result in the $z$-axis is shown in Fig. 3(a).

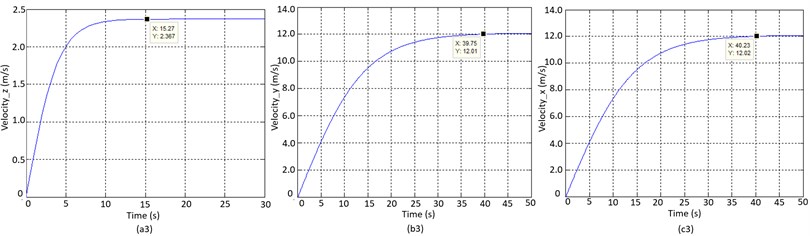
If pitch angle and yaw angle are zero, roll angle is approximately 5 degrees; then Quadcopter moves along the $y$-axis. The motion of the quadrotor in Fig. 3(b) and Fig. 4(a) is demonstrated below. From the results, settling time is 1,73 s approximately, and overshoot is 32,6 % which must be less than ±3^o):

In this case, the system tries to achieve the predetermined attitude on the $z$-axis during the first 10 s. Therefore, the slope of the position graph on the $y$-axis is low. Similarly, the roll angle and yaw angle are zero. Pitch angle equals -5 degrees, and then the drone moves along the $x$-axis. The Trajectory of Quadcopter in Fig. 4(b) and Fig. 3(c) is computed as follows. It is measured that settling time is 1,59 s roughly and overshoot is 27,3 %:

Fig. 3Simulation results of system parameters on a) Z-axis, b) Y-axis, and c) X-axis

a)

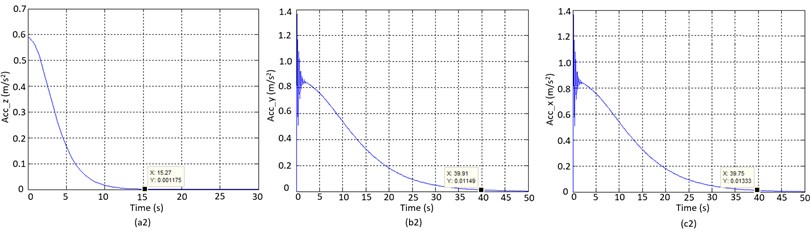
b)

c)

Fig. 4Simulation results on a) pitch angle and b) roll angle

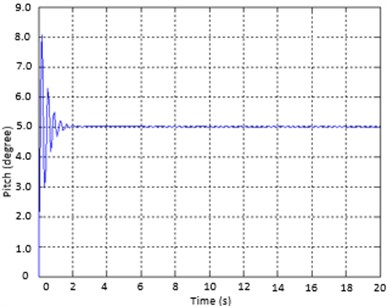
a)

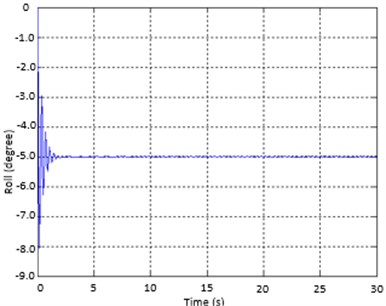
b)

With out best knowledge, to achieve the better performance, the tuning process of filter is reasonably based on our experiences. For the pitch angle estimation, the component in high frequency is from the integrating pitch rate of gyro output while using the sensitivity of accelerometer to gravity direction is for the one in low frequency. The gain $\gamma$ is tuned so that the estimated angle is wholly compensated in steady state. Similarly, the trial-and-error approach is appropriate to adjust the proper values for covariance matrix in Kalman filter. Using the above constraints, it is programmed in Matlab environment to mimic the performance of aerial vehicle in 3D space as Fig. 5(a). To imitate the real-world circumstance, the Gaussian function that plays as noise, is added to the system model. The output responses of velocity, acceleration and compass are gained in Fig. 6 in respect to data from gyroscope, accelerometer and compass measured sensor. Consequently, it can be understood clearly that these results of proposed design are reasonable and feasible.

Fig. 5a) Theoretical simulation of tracking trajectory and b) experimental test in practice

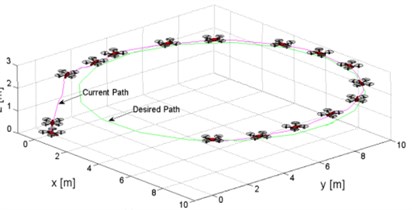
a)

b)

Fig. 6Simulation results of feedback signals from a) gyroscope, b) accelerometer and c) compass sensor

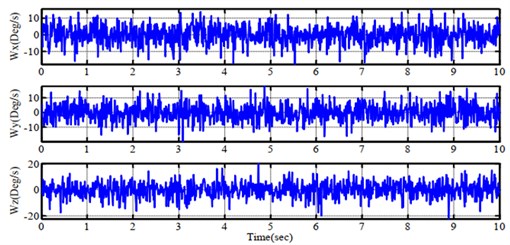
a)

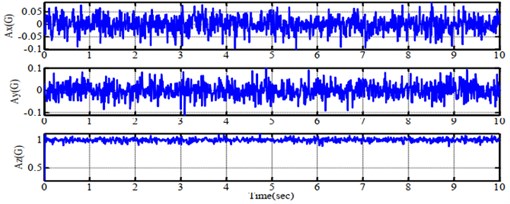
b)

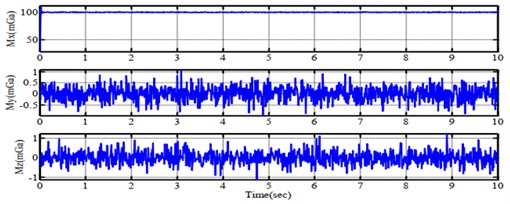
c)

6. Results of experimental validation

In these experiments, the previous section's design is employed to verify as follows: open-loop control scheme in $x$, $y$, and $z$-axis, PID control scheme in roll angle to drive left or right, and PID control scheme in pitch angle to drive forward or backward. The gains $K_P$, $K_I$ and $K_D$ of PID controller are 1.3, 0.004 and 18 respectively. To control the exact yaw angle is not a topic in this research. BoosterPack module is attached to the drone and is supervised by mobile and host through GUI. $\gamma$, for Complementary filter, varies from 0.96 to 0.98 and $R$, for Kalman filter, is 0.6~0.8 so that the sensor achieves good performance. As a result, they are selected as the best suitable values ($\gamma =$0.9725, $R=$0.6137).

Fig. 7Experimental performance of feedback signals from a) gyroscope, b) accelerometer and c) compass sensor

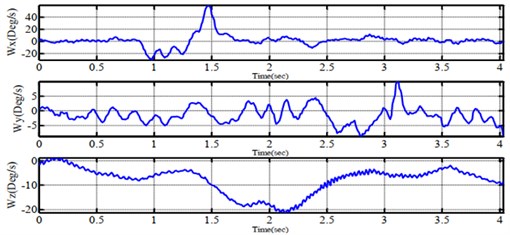
a)

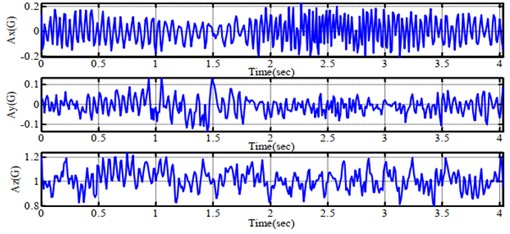
b)

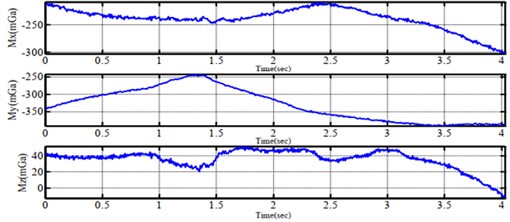
c)

In the initializing stage, the CPU sets predetermined values for inputs, outputs, and peripheral devices when power is on. The main program will run in a loop as order; i.e. (1) Read raw data from the attached sensors; (2) Process data via sensor fusion filter (Kalman filter or Complementary filter); (3) Read RF signal from a remote controller, combine with handling values from the filter, these signals are inputted in the PID scheme to compute pulses for motors; (4) After delivering pulses to ESC, CPU transfers feedback data to a ground station.

In Fig. 7(a) and Fig. 7(b), the Complementary filter gets values of the gyro as major factors and accelerometer values as minor sources. Hence, the fluctuation which is created by both motors and propellers, indicates the accelerometer's angles. The evaluated angle from Complementary filter is more constant than that of the Kalman filter. Nonetheless, the drift phenomenon of about ±0,5° still remains. On the other hand, the Kalman filter's performance in Fig. 8(a) and Fig. 8(b) obtains the angles from an accelerometer to calculate the practical angle. It mentions the fact that this filter carries out more precise values than it was expected. However, the pulse modulation signal to each driving motor belongs to the vibration of the system.

Fig. 8Experimental performance of errors for a) roll angle, b) pitch angle and c) yaw angle when testing on one-axis by complementary filter

a)

b)

c)

In order to examine the balancing capability on one axis, the experiment in Fig. 9(a) is performed to investigate the hardware of the system. This aerial system is suspended on a stick, and the controller tries to keep the fixed angle of 10, 30 and –35 degrees. In Fig. 10, several angular values are obtained by testing on one axis. The system testing is started in 1.5 s and the system is balanced in 5 s. Later, a stick is turned to the left, the point is balanced during 3 s. The AAS retains the predetermined angle within 8 s.

Fig. 9Experimental balancing test on a) one-axis and b) six-axes

a)

b)

In the test scenario of six-axes motion shown in Fig. 9(b), four wings are free, and the body frame is hung by a shaft in order to evaluate the balancing ability. In Fig. 11, the experimental results of tracking angles are completed by Complementary filter correspondingly whilst Fig. 12 reveals the errors of angular values. At the sequence of 3 s, the whole system is turned on. After a few seconds, the aerial vehicle is elevated from the ground and reached to a stable position. Again, in Fig. 13 and Fig. 14, the same test conditions are employed for the Kalman filter. The autonomous aerial vehicle can slightly fluctuate around the equilibrium point with ±3 degrees, though it bears the external disturbances in the outdoor surrounding. From the above results, it can be understood easily that theComplementary filter is more advantageous than the Kalman filter in the view of the simple implementation and easy understanding. However, the filtering results from the Kalman filter produce better precision and stable performance. There is a trade-off between the Complementary filter and Kalman filter when they are integrated into the autonomous system. In Fig. 5(b), quadrotor performs well while the PID controller adapts with excellent tuning parameters based on the experiences of operator.

Fig. 10Experimental performance of errors for a) roll angle, b) pitch angle and c) yaw angle when testing on one-axis by Kalman Filter

a)

b)

c)

Fig. 11Tracking performance of a) roll angle, b) pitch angle and c) yaw angle when tesing on six-axes by complementary filter

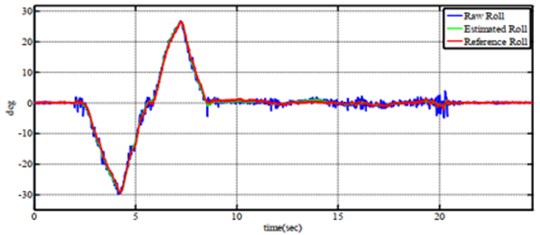
a)

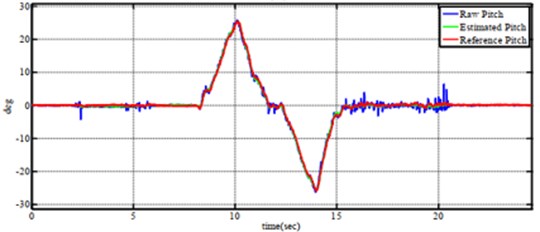
b)

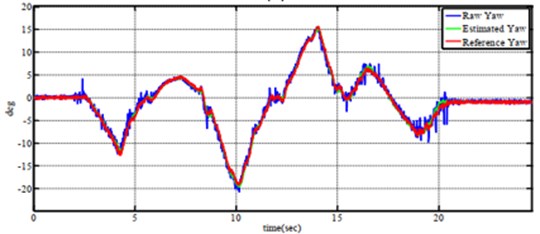
c)

Fig. 12Experimental performance of errors for a) roll angle, b) pitch angle and c) yaw angle when tesing on six-axes by complementary filter

a)

b)

c)

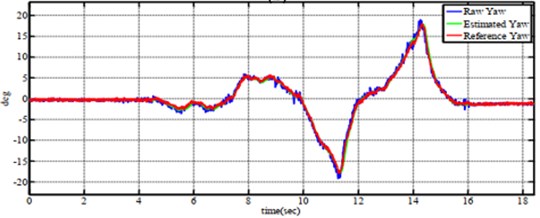
Fig. 13Tracking performance of a) roll angle, b) pitch angle and c) yaw angle when tesing on six-axes by Kalman Filter

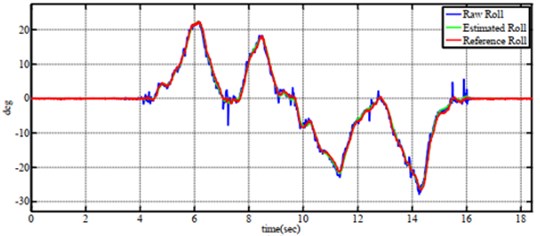
a)

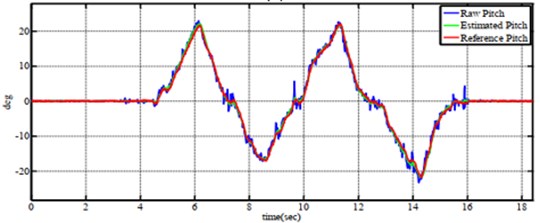
b)

c)

Fig. 14Experimental performance of errors for a) roll angle, b) pitch angle and c) yaw angle when tesing on six-axes by Kalman Filter.

a)

b)

c)

To summarize the technical specifications, the competitive descriptions among related researches have been indicated in Table 3. The outcomes of each approach were noted to illuminate the main advantages and the applied fields.

7. Conclusions

In this paper, the comparative investigation of Complementary filter and Kalman filter for the aerial vehicle control is made. Firstly, a theoretical model is applied to estimate the orientation and acceleration. Then, the developmental theory of two filters is launched to realize the innovative idea. These works are later employed in the platform of AAS to insist on major factors in both filters while the kinematics and dynamics of the quadrotor are analyzed in terms of implementation. Based on the numerical simulation and experimental tests, the proper selection of effective filters for low-cost, feasibility, and practical applications in the environment, automation, and agriculture has been validated.

Future perspectives shall be mentioned. From these results from both simulation and experiment, the data fusion has a potential to be investigated among different sensing instruments such as digital camera, inertial sensor and positioning sensor in order to enhance the system performance. In the other approach, the advanced control scheme that automatically adjusts the tuning gains of filter should be noticed. Moreover, the integrating design of both Kalman and Complementary filter into one platform may be more advantageous.