Signal enhancement in wireless sensor networks based on adaptive filters

2.1. Research on application model based on adaptive filtering algorithm

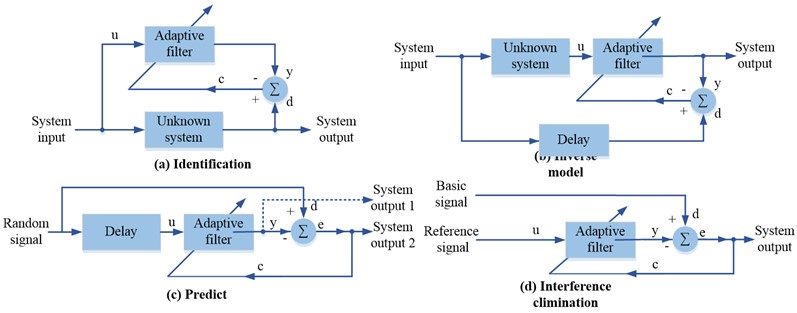
Traditional filters are divided into high pass filter, low pass filter, band stop filter and band pass filter, which can respectively pass signals corresponding to different frequency components. The advantage of the adaptive filter over the traditional filter is that the adaptive filter can automatically update its own parameters through the adaptive filtering algorithm in an unknown environment, and the weight coefficient vector of the filter will also be automatically adjusted in time, thus effectively tracking the time-varying characteristics of the input signal. The adaptive filter has great correlation with its parameters and signal data, so the filter can be divided into linear system and nonlinear system according to whether its “input output” meets the superposition principle [17]. Linear adaptive filtering algorithm mainly consists of normal filtering process and adaptive process. The filtering algorithm first outputs the input signal normally, and then feeds back some parameters of the previous output to the next input for adaptive process [18]. The two processes cooperate and influence each other. Adaptive filters are used in identification, inverse model, prediction and interference elimination because of their strong adaptability to complex environments. Fig. 1 shows the four application types of adaptive filters.

The classical adaptive filtering algorithms are divided into three basic types: least mean square algorithm (LMS), recursive least square algorithm (RLS) and radial projection algorithm (AP). Among them, the least mean square is the most widely used in practice because of its small amount of calculation and simple algorithm form. This method mainly reduces the complexity of the algorithm by modifying the gradient vector of the objective function. The core idea of LMS is the steepest descent method, which is mainly divided into filter output, estimation error and filter tap weight update. For the output of the filter, its equation can be expressed as:

where, $y\left(n\right)$ represents the output signal of the filter, $X\left(n\right)$ represents the input signal of the filter, and $W\left(n\right)$ represents the weight coefficient of the filter. If $e\left(n\right)$ is defined as error signal and $d\left(n\right)$ as expected signal, there is a equation:

Fig. 1Four basic application types of adaptive filters

Eq. (2) represents the error signal of the filter. Taking the minimum mean square value of the error signal as the optimal criterion, the cost function can be expressed as:

where, $J\left(n\right)$ represents the cost function, and its change over time can be used to represent the convergence rate and convergence accuracy of the filter. When the value of $J\left(n\right)$ is the smallest, it means that the weight coefficient of the filter is optimal. The adjustment of the filter weight vector can be realized by the steepest descent method, that is, along the negative gradient direction of the performance surface. Search the minimum point in the performance surface to solve the optimal weight vector. The adjusted weight vector equation can be updated as follows:

where, $\mu$ represents the step convergence factor of the filter. When the value of is large, the convergence speed of the algorithm is fast but accompanied by large steady-state error; When the value of $\mu$ is small, the convergence speed of the algorithm is small but the steady-state error will be reduced. It can be seen that the value of $\mu$ directly affects the performance of the algorithm. To balance the steady state error of the filter with the convergence speed, the step factor $\mu$ needs to be conditionally constrained:

Eq. (5) represents the constraint condition of step factor $\mu$, where $L$ represents the order of the filter and $S_{\mathrm{m}\mathrm{a}\mathrm{x}}$ represents the maximum value of the power spectral density of the input signal. LMS adaptive filter contains two basic processes: filtering and adaptation, which form a feedback loop, and its operation is simple and easy to implement. Compared with LMS algorithm, RLS algorithm has more computation and faster convergence speed. After the optimal weight coefficient vector is also solved, the approximate equation is obtained through LS criterion:

where, $\lambda$ represents the forgetting factor, whose value range is from 0 to 1, and $Z\left(n\right)$ is a matrix of $L\times L$. The iterative equation of the filter weight coefficient vector of RLS is:

Eq. (7) shows the complex operation property of RLS algorithm. During its iteration, $L^2+3L$ addition, $L^2+5L+1$ multiplication and 1 division are required for real signal. For complex signals, $4L^2+12L-1$addition, $4L^2+16L+1$ multiplication and 1 division are required. The AP algorithm is applicable to adaptive filters when the input signals are highly correlated. Compared with LMS algorithm and RLS algorithm, AP algorithm has the advantage of “memory”. It can not only use the current input signal, but also reuse the input signal at a certain time in the past. The data input matrix is as follows:

where, $LP$ represents the matrix of order $L\times P$, $L$ represents the length of the filter, and $P$ represents the number of times the AP algorithm uses data. The AP algorithm takes the expectation vector equal to the product of the input matrix and the weight vector as the constraint condition to minimize ${‖h\left(n+1\right)-h\left(n\right)‖}_2^2$. The weight coefficient vector iteration equation of AP algorithm is expressed as:

where, $e\left(n\right)$ represents the error vector. In order to avoid that the denominator value in Eq. (9) is 0, the regularization parameter $\delta$ is introduced. At the same time, the step factor $\mu$ is introduced to reduce the steady state error of the algorithm, so the weight coefficient vector iteration equation of the AP algorithm can be transformed into:

where, the value range of step factor $\mu$ is 0 to 2. The above three algorithms are the classical types of adaptive filters, and they have their own advantages. The theory of adaptive filter has been developing and improving constantly, and its application in the field of communication has always been exclusive. In order to better deal with the input signal interfered by noise, a deviation compensated normalized cross entropy algorithm (BCNMCC) is proposed to suppress the input noise signal, which is especially suitable for non Gaussian noise environment.

2.2. Construction of signal enhancement model of wireless sensor network combined with adaptive filter

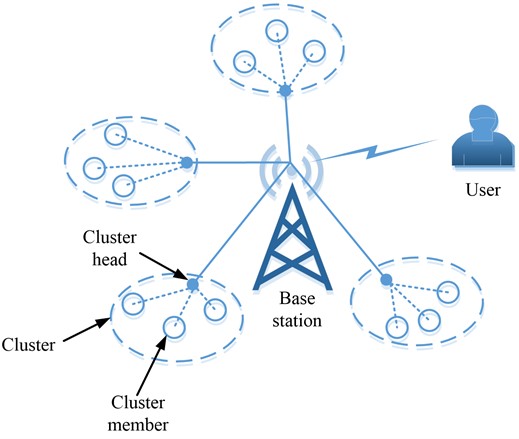
Wireless Sensor Network (WSN) is a distributed communication network that deploys a large number of energy constrained sensor nodes, with the characteristics of multi hop and self-organization. Wireless sensor networks are widely used in military, medical, industrial and detection fields. Figure 2 shows the topology of a wireless sensor network, which uses clustering routing to divide the network into several sets of network nodes with some association [19]. The signal enhancement of wireless sensor network can be realized by using the adaptive beam formed by the adaptive filtering algorithm. The adaptive filtering algorithm can adjust the different weights of each signal in the wireless sensor to improve the output signal-to-noise ratio of the wireless sensor. The algorithm can suppress the interference signal by adjusting the weight adaptively, so as to enhance the expected signal.

Fig. 2Topology of wireless sensor networks

Wireless sensor network is a distributed network. In view of this feature, the experiment proposes an adaptive consumption based linear distributed filtering (ACLDF) algorithm, which integrates adaptive weighting, to better meet the needs of wireless sensor networks for improving estimation accuracy and enhancing signals. Distributed estimation algorithm has the characteristics of fast convergence, high estimation accuracy, strong robustness, etc. Many researchers have made research on this, and the experiment will carry out a comparative study of algorithm performance [20]. Considering the possible packet loss in sensor networks, the support relationship between sensor nodes' measurement data is defined first, and the support is linearly weighted to obtain the estimation confidence of each node to the target. After that, the fusion weight composed of the reliability is introduced into the consistency principle of the node state estimation to dynamically adjust the weight. Suppose that an existing wireless sensor network containing $n$ sensors is in the target system interfered by a Gaussian noise at the moment, and the state model and observation model of the system are:

where, ${\lambda }_i$ represents a binary random value. When ${\lambda }_i=0$ is used, it indicates that the data packet of node $V_i$ is lost. $x\left(k\right)$ it represents the state vector of the system at time $k$, and $z_i\left(k\right)$ represents the observation vector of sensor node $V_i$ at time $k$. $A$ represents the system state transition matrix, and $H_i$ represents the observation matrix of sensor node $V_i$. $w\left(k\right)$ represents the process noise of the system at time $k$, and $v_i\left(k\right)$ represents the observation noise of sensor node $V_i$ at time $k$. The calculation equation of node importance of sensor network is:

where, ${\mathrm{\Gamma }}_b\left(i\right)$ represents the number of shortest paths passing through node $V_i$, and ${\mathrm{\Gamma }}_c\left(i\right)$ represents the centrality of node $V_i$. If the value of $K_i$ is larger, it means that the node has greater influence on the network and is more important in the network. The support equation between two nodes can be expressed as:

Eq. (13) represents the relative distance between the state estimates of node $V_i$ and node $V_j$ in the sensor network. The smaller the value of $d_{ij}\left(k\right)$ is, the smaller the difference between the state estimates of the two nodes at time $k$ is, and the higher the mutual support is. The support equation of node $V_i$ in the whole network can be expressed as:

where, ${\gamma }_{i1}\left(k\right)$ represents the support degree of node $V_i$ and other nodes, and $\sigma$ is a group of negative parameters obtained from the normalization of node importance of node $V_i$ in the sensor network. The gain matrix of each sensor node in the network can be expressed as:

where, $A$ represents the state transition matrix, and $Q$ is the system process noise covariance matrix. $H$ represents the sensor node observation matrix, and $c$represents the parameter, whose value range is 0.2 to 0.8. The sensor network with adaptive weighted distributed filtering algorithm is as shown above. The model considers the attributes of the node itself and its influence in the network, and linearly weights the importance and support of the node to obtain the estimation confidence of each sensor node to the target. The fusion weight composed of the reliability is introduced into the estimation value of the target state by the sensor node to improve the estimation accuracy of the filtering algorithm. Next, the experiment will verify the estimation accuracy of the model and the signal enhancement effect on wireless sensor networks.

3.1. Comparative analysis of adaptive filter performance

To verify the performance advantage of the adaptive filter over the traditional filter, a sine signal with a frequency of 2 kHz is set in the experiment, as shown in Fig. 3(a). It is assumed that the signal is interfered by noise during its transmission to form a useful interfered signal, which is used as the input signal of traditional filter and adaptive filter, as shown in Fig. 3(b).

Fig. 3Experimental signal setting

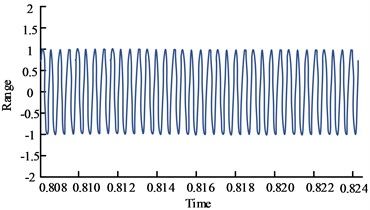
a) Useful signal (2 kHz sine signal)

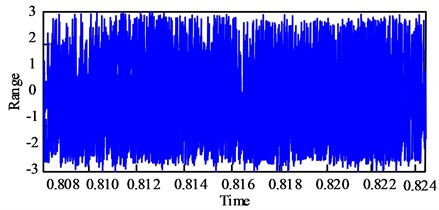
b) Disturbed useful signal

In this study, Matlab platform was used for experiments, that is, the signal interfered by random noise was input into the traditional filter and adaptive filter based on Matlab platform, and the noise cancellation effect was observed. The signal affected by noise in Fig. 3(b) was interfered by traditional filter and adaptive filter, and the experimental results shown in Fig. 4 were obtained. It is not difficult to find from the results in the figure that the signal curve obtained by the adaptive filtering algorithm after noise elimination is smoother and more stable than that of the traditional filter, and its fluctuation amplitude is more balanced. The results show that both filtering algorithms can eliminate noise to a certain extent, but the effect of traditional filter is much weaker than that of adaptive filter. The main reason is that the adaptive filter can adjust the weight coefficient adaptively according to the algorithm to cope with various unknown environments, so it has better noise elimination and filtering effect than the traditional filtering algorithm.

Fig. 4Comparison of noise cancellation effects between two filters

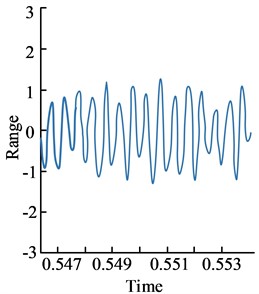
a) Output result of traditional filter

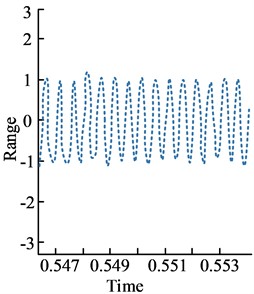
b) Output result of adaptive filter

Fig. 5Convergence performance of four algorithms under different pulse intensities

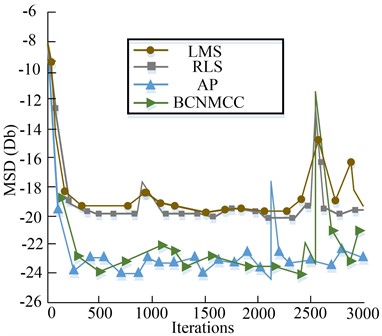
a) Small pulse measurement noise

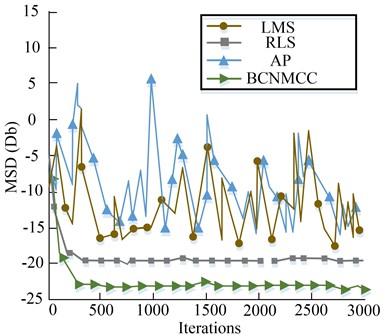
b) Strong pulse measurement noise

Subsequently, the performance of the above three adaptive filtering algorithms (LMS, RLS, AP) and the improved BCNMMC algorithm based on them is verified by experiments. Fig. 5 shows the simulation results of four adaptive filters at different pulse noise levels. Fig. 5(a) shows the convergence performance of the algorithm in the environment of small impulse noise, and Fig. 5(b) shows the convergence performance of the algorithm in the environment of strong impulse noise. In the case of small pulses, RLS and AP have relatively smooth accuracy. The peak value of the experiment appeared at about 2500 iterations, which was probably caused by pulse interference. The RLS and BCNMCC adaptive filtering algorithms have good stability and convergence in the case of strong pulse. In addition, the steady-state accuracy of AP and BCMCC is lower than that of the other two algorithms when the convergence rate is the same.

Table 1 summarizes the comparative advantages of the four adaptive filtering algorithms. Among them, the three classical traditional algorithms can occupy some advantages, and the BCNMC algorithm proposed by relevant research integrates these advantages more comprehensively, which can have better adaptability in the noise environment of non-Gaussian measurement, and can effectively suppress the deviation caused by input noise. It can be seen that the adaptive algorithm filtering algorithm has a strong function in eliminating the noise of the input signal, and has a good applicability in network signal enhancement.

3.2. Performance verification of wireless sensor network signal enhancement model of adaptive filter

According to the distributed characteristics of sensor networks, this paper proposes a distributed filtering algorithm based on adaptive filtering algorithm (ACLDF), which integrates adaptive weighting. In the simulation experiment, 30 sensors are randomly scattered in a square area of 400 m², with an effective network communication radius of 8m. The parameter settings of the system matrix are shown in Table 2. In order to better compare the performance of the proposed model, the experiment selects the consistent linear distributed filtering (CLDF) algorithm and the consistent filtering with packet dropping (CFPD) algorithm for comparison and verification.

Fig. 6 shows the comparison results of sensor node estimation errors under ideal conditions. It can be seen from the figure that in this state, the curve of ACLDF proposed by the experiment is more smooth, which shows that its estimation performance is better than the other two algorithms. The main reason for this result is that the ACLDF algorithm can uniformly process the estimated values obtained by the filter, which improves the estimation accuracy of sensor nodes to a certain extent. Therefore, the estimation error of ACLDF is smaller than that of the other two algorithms, and it has faster convergence speed.

Fig. 7 shows the estimation error results when any three nodes in the network are attacked under the random attack mode. In this mode, the ACLDF algorithm can improve the estimation accuracy of the entire sensor network and the state estimation value of each sensor network node, so that the estimated value of network nodes can be more closely distributed near the true value. The improvement of its estimation accuracy and algorithm performance is conducive to promoting the performance of sensor networks, including noise processing and other aspects, to a certain extent, is conducive to the enhancement of its network signal.

Fig. 6Comparison effect of node estimation error

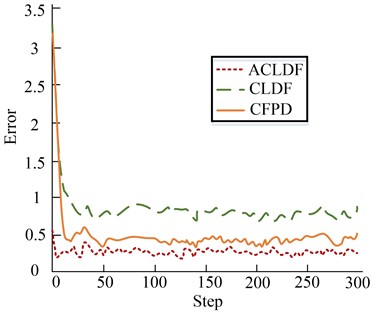
a) Comparison chart of estimation error

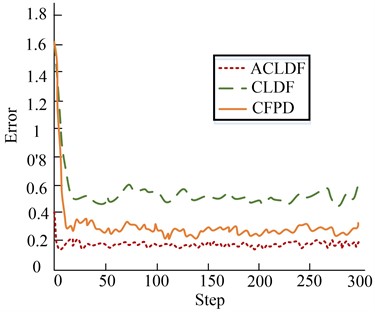
b) Comparison chart of inconsistent estimation error

Fig. 7Comparison of average estimation error of network nodes under random attack mode

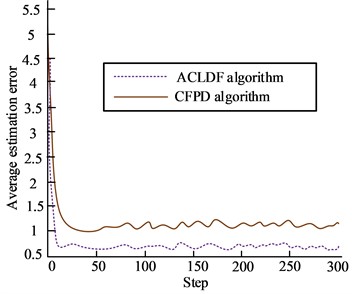
a) Comparison chart of average estimation error under random attack mode

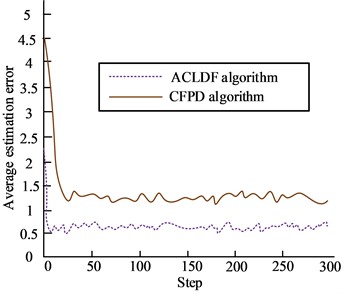
b) Comparison chart of inconsistent average estimation error under random attack mode

Fig. 8Comparison of average estimation error of each node under selective attack mode

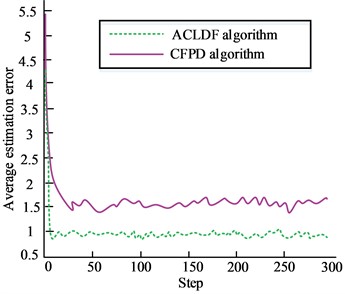
a) Comparison chart of average estimation error under selective attack mode

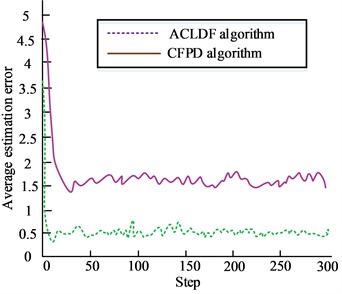
b) Comparison chart of inconsistent average estimation error under selective attack mode

At the end of the experiment, the nodes of the sensor network are sorted according to the degree of confidence, and three networks with high degree of confidence are selected to attack. The experimental results are shown in Fig. 8. It can be seen from the figure that the ACLDF algorithm can reduce the estimation error of the algorithm and improve the estimation accuracy of the model to a certain extent, and the state estimation values of each node in the sensor network can be more closely distributed near the real value. When some important nodes in sensor networks are attacked, selective attacks can cause greater impact than random attacks. This shows that in practical applications, it is necessary to increase the maintenance of network nodes with high confidence, and ensure the stability of sensor network signals while maintaining good network estimation accuracy. The sensor network with strong anti attack capability is conducive to the stability and enhancement of its network signal, and can maintain an efficient working state.