Dynamic analysis on the structure of metro station under high-speed railway load

2.1. Site introduction

Fig. 1(a) shows the plan view and elevation view of the site for Jinqiao Station. The Jinqiao Station of Nanning metro line 5 were constructed using cut and cover method. This station has a long and narrow shape. The length and width of the excavation are 597.3 m and 19.2 m, respectively. The excavation depth of partrange from 18.2 to 20.7 m. Bore pile was adopted as the retaining structure for the excavation. The diameter and spacing of the bore pile is 1.2 m and 1.4 m, respectively. The length of the pile is 25 m. Jet grouting pile was used for the purpose of waterproof. Three layers of strut were designed inside of the excavation. The first layer of struts is concrete strut, while the struts for the rest two layers are steel strut. The arrangement and the dimension of the struts is shown in Fig. 1(b).

The first layer of soil in this site is fill with a thickness of about 6 m. The second the layer of soil is also fill with different parameters from the first layer. Below the two layers of fill, there is a thin layer of clay with a thickness of 2 m. Clay stone lays below the clay. The parameters of the soil can be referred to Table 1.

Fig. 1Schematic diagram of the site of Jinqiao Station

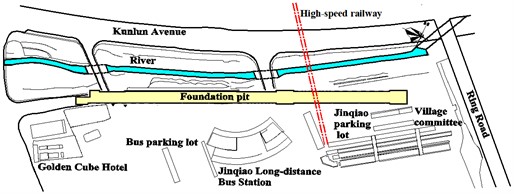
a) Plan view

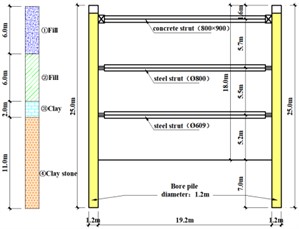
b) Elevation view

2.2. Finite element mesh and boundary conditions

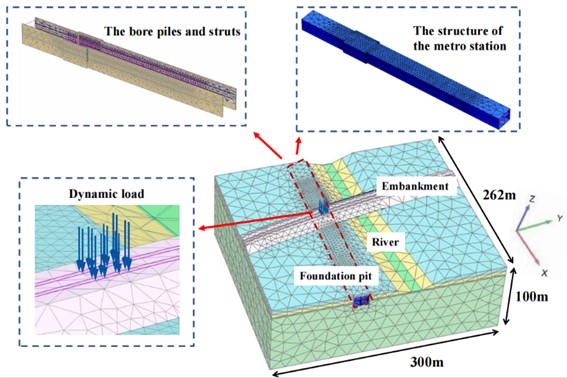
Fig. 2 shows the three-dimensional finite element mesh for the numerical analyses. The geometry of the mesh was the same as that in the site. Roller supports were applied on all vertical sides of the mesh and pinned supports were assigned to the base of the mesh. The total length of the model is 300 m and the width of the model is 262 m. The model has a depth of 100 m. In total, this model contains 109687 elements and 150794 nodes. The bore pile was modeled as a thick with an equivalent thickness of 0.623 m. The structure of the metro station was modeled using plate element considering the interaction with the retaining structure (i.e., bore pile). The struts are modelled using beam elements. The embankment and the dynamic load were modelled according the design document. The parameters of soil were adopted according to the geotechnical investigation report of this site.

Fig. 2Three-dimensional numerical model

2.3. Constitutive model and model parameters

It is known that the small strain stiffness is of great significant for the excavation-induced deformation problems [6]. In this study, the hardening soil model with small-strain stiffness was adopted forfill, clay and clay claystone. The numerical parameters are adopted based on the geotechnical investigation report. According to Plaxis manual [7], the reloading modulus, Eur, is taken as three times of the secant modulus, E50 for fill, clay and clayclaystone. For fill, clay and claystone, Eur is adopted as six times of the E50. The soil parameters used in this study are summarized in Table 1. The bore piles, struts and structure of metro station are modelled as linear elastic materials. The elastic modulus of concrete and steel are adopted as 30 GPa and 200 GPa, respectively.

2.4. Numerical modelling procedures

Table 2 shows the numerical modelling procedure of this study. The numerical modelling procedure follows the construction procedures of this site. In order to model the initial stress state of the model, the construction process of the excavation was considered. The excavation was divided into three steps. Struts are installed after each excavation steps. The ground water level is assumed to be 0.5m below the formation level.

3.1. Vibration force induced by high-speed train

Fig. 3(a) shows the vibration force induced by high-speed train under a speed of 160 km/h. According to Liang and Cai [8], the vibration force can be calculated using the following equation:

where $P_0$ is static load of train wheels, $P_1$ is vibration load of a typical value under stable state, $P_2$ is vibration load of a typical value under the control condition according to the dynamic additional load acting on the line, $P_3$ is vibration load of a typical value under waveform abrasion control, $\omega$ is circular frequency of rough vibration wavelength under three control conditions at corresponding vehicle speed. And the calculation formula of $P_i$ is $P_i=M_0{a}_i{\omega }_i^2$, where, $M_0$ is the unsprung mass of the train, and the value is 750 kg, the $a_i$ is the typical vector height under the three control conditions of corresponding vehicle speed. The calculation formula of ${\omega }_i$ is ${\omega }_i=2\pi \frac{v}{L_i}$, where, $v$ is the train running speed, and $L_i$ is the typical wavelength under the three control conditions.

A time span of 0.5S are adopted in this study. As shown in Fig. 3(a), the maximum vibration force is 115 kN, while the minimum vibration force is 89 kN. The average vibration force is 102 kN. Fig. 3(b) shows the vibration force induced by high-speed train under a speed of 350 km/h. A time span of 0.5S are also adopted. The maximum vibration force is 164 kN, which is 42.6 % larger than that under a speed of 160 km/h. Meanwhile, and the minimum vibration force is 40 kN, which is 55.1 % smaller than that under a speed of 160 km/h. The average vibration force is also 102 kN, which is equal to that under a speed of 160 km/h.

Fig. 3Vibration force induced by high-speed train

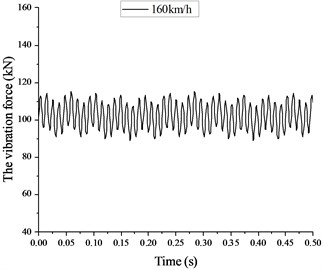
a) Under a speed of 160 km/h

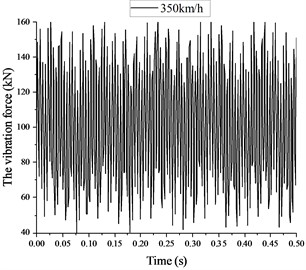
b) Under a speed of 350 km/h

3.2. Vertical vibration acceleration along depth

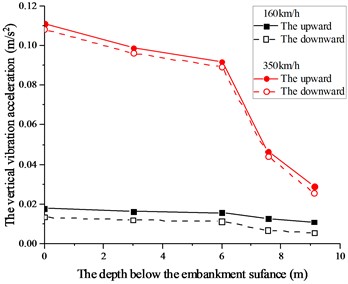
Fig. 4 shows the vertical vibration acceleration along the depth below the ground surface. The upward vibration acceleration and the downward vibration acceleration both decrease with the increase of depth below the embankment surface. In addition, the decreasing rate of the vertical vibration acceleration increased significantly when the depth is larger than 6 m under a speed of 350 km/h. The trend of the downward vibration acceleration is similar to the upward vibration acceleration. However, the value of the downward vibration acceleration is about 20 % lower than the upward vibration acceleration. The trend of curve for a train speed of 350 km/h is similar to that under a speed of 160 km/h, but the magnitude of the vibration acceleration is significantly larger.

Fig. 4Vertical vibration acceleration along depth

3.3. Bending moment of metro station

Fig. 5(a) shows bending moment of top slab, middle slab and bottom slab under a train speed of 160 km/h. The maximum bending moment of top slab occurs at the portion with a larger width (please refer to Fig. 1). This may indicate that the geometry arrangement of the underground structure can influence the bending moment of structure induce by dynamic load. The maximum positive and negative bending moment are 793.0 kN·m/m and –885.9 kN·m/m, respectively. Compared to the top slab, the bending moment of middle slab and bottom slab are negligible. This may be because the top slab is closer to the dynamic load.

Fig. 5(b) shows bending moment of top slab, middle slab and bottom slab under a train speed of 350 km/h. The distribution of bending moment of top slab, middle slab and bottom slab is similar to that under a train speed of 160 km/h. In addition, the magnitude of the bending moment is also close to that under a train speed of 160 km/h. The maximum positive and negative bending moment are 795.2 kN·m/m and –888.2 kN·m/m, respectively. It seems the speed of train has an insignificant influence on bending moment of top slab, middle slab and bottom slab.

Fig. 5Bending moment (M11) of top slab, middle slab and bottom slab

a) Under a speed of 160 km/h

b) Under a speed of 350 km/h

Fig. 6(a) shows bending moment of side wall and middle wall under a train speed of 160 km/h. The maximum bending moment occurs at the middle wall. This may be related to the arrangement of structure of metro station. The maximum positive and negative bending moment are 127.2 kN·m/m and –87.04 kN·m/m, respectively.

Fig. 6(b) shows bending moment of side wall and middle wall under a train speed of 350 km/h. Generally, the bending moment of side wall and middle wall under a train speed of 350 km/h is larger than that under a train speed of 160 km/h. This means the speed of train has a significant influence on bending moment of side wall and middle wall. This is different with the bending moment for top slab, middle slab and bottom slab. The maximum positive and negative bending moment are 136.3 kN·m/m and –148.2 kN·m/m, respectively. Both the maximum bending moment induced in the structure of metro station is within the structure capacity of the structure.

Fig. 6Bending moment (M11) of side wall and middle wall

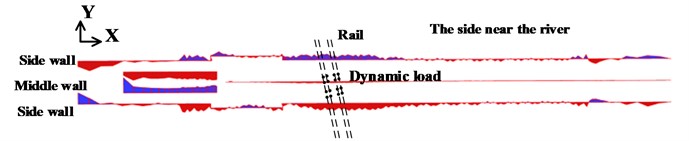
a) Under a speed of 160 km/h

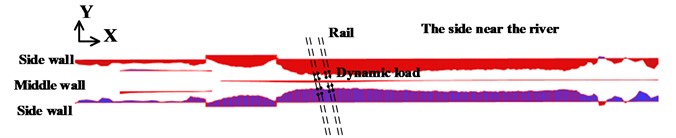
b) Under a speed of 350 km/h