Super resolution direction finding technique of vortex electromagnetic wave radar in missing mode

3.1. Super-resolution direction finding technique for vortex electromagnetic wave radar based on ASSGD missing mode recovery

For some modes of vortex waves, the scattered echoes from the scattered body under test are attenuated, resulting in the phenomenon of missing modes. When the modes are missing, the super-resolution method suffers from reduced resolution, increased partials and increased peak partials, which in turn reduces the azimuth spectrum resolution and prevents a clear image of the target from being obtained. Due to the missing modes, the azimuth spectrum imaging quality of the radar is significantly degraded. How to improve the super-resolution capability of the vortex EM wave radar under missing modes is an urgent problem to be solved.

When a vortex electromagnetic wave radar operates, the modes are received in sequence, with the power value of their background noise as the recognition threshold. During reception, the energy share of the mode is counted and if the energy level of the dominant mode is lower than the background noise, the mode is considered not to have been received correctly, i.e. the mode is missing. When the target is at rest, the vortex radar echo is seen as a superposition of signals from multiple targets, such that both the valid and missing modes acquired by the vortex radar have the same azimuthal spectral component. The missing modes can then be recovered from these valid modes to obtain better azimuthal spectral results.

Assuming that there are $N$ samples of received modes, if there is a case where the primary mode energy of a received mode exceeds the discrimination threshold, it is included in $N_{g\left(i\right)}$, where, $i=\mathrm{1,2},...q$, is used to describe the set of samples of consistently normally received modes [12]. Conversely, if a situation arises where the received modal major mode energy is below the discrimination threshold, it is included in $N_{m\left(i\right)}$, the set of samples of missing modes, and a sketch of the sampling segments for valid and missing modes is shown in Fig. 1.

Fig. 1Sampling section diagram of effective mode and missing mode

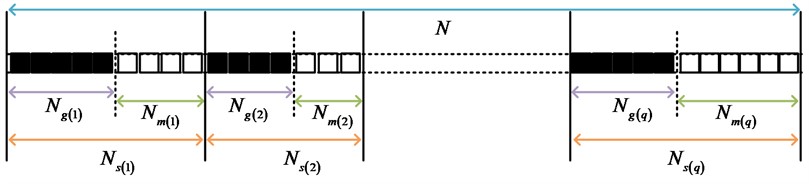
In Fig. 1, the $N$ received modal samples are divided into a valid modal subset $N_g$ and a missing modal subset $N_m$. the $N_g$ and $N_m$ are represented using a matrix with the expression shown in Eq. (1):

In Eq. (1), $y_g$ and $y_m$ are used to describe the data matrix in the normal reception mode and the missing mode, then $y$ is meant to be the data of all the modes that should be received [13].

In response to the current situation of missing modes in the OAM modal data $y$ acquired by the vortex radar, the use of existing super-resolution methods will result in low resolution and the inability to perform high partials, so in order to estimate the vortex radar azimuth spectrum more accurately, the missing mode sample $y_m$ needs to be estimated in $y_g$.

The gradient descent algorithm (GDA) is based on the sparsity of the target along the azimuthal spectrum, with the sparsity of the signal as the optimisation objective. Usually, the azimuthal spectral parametrization decreases exponentially and can be considered as 0 when it is below a certain threshold, while when it is above the threshold, the amount is the sparsity of the signal. The ideal fully sampled modal sample would result in a very low azimuthal spectral sparsity, while a modal deficiency would result in an increase in azimuthal spectral sparsity, which could be raised to the optimisation objective. The Adaptive Step Size Gradient Descent (ASSGD) algorithm can adaptively adjust the step size within each gradient descent cycle, thus improving the convergence and accuracy of the algorithm.

When the number of targets is smaller than the number of signal samples, the signal is considered to be sparse in the orientation domain. A sparse signal is able to be recovered from a small number of sample signals by a full signal. In practice, when the signal is represented as sparse in the transform domain, the sampled data is usually used as the observed data. gda uses the lost sample signal as a variable, and the complete signal is diluted in the transform domain, i.e. the degree of sparsity obtained is reduced, by modifying the corresponding rule at each iteration for the lost sample data [14].

For missing modal data, GDA treats its normally received modal signal value as a constant and treats the sampled value of the missing modal signal as a continuous variable. Denote the sparsity of the signal $y$ by ${‖T\left\{y\right\}‖}_1$, where ${‖\cdot ‖}_1$ is used to describe the matrix ${\mathcal{l}}_1$ parametrization, and then $T\left\{\cdot \right\}$ represents the linear transform, which is generally obtained by the discrete Fourier transform of the signal $y$, or ${‖T\left\{y\right\}‖}_1={‖dft\left[y\right]‖}_1$.

Firstly, the initial signal $y$ will represent the data of the full pattern received, where the missing data $y_m$ will be given an initial value of 0, and the initial iterative signal will be defined with the expression shown in Eq. (2):

where $\left(0\right)$ is used to describe the first iteration of the algorithm [15]. Then, regarding the missing mode at $N_m$, two signals, $y_{+}$ and $y_{-}$, are formed at the $i$th iteration, and the expression for $y_{+}$ is shown in Eq. (3):

where, $n_j=\mathrm{1,2},...,N$, and $\mathrm{\Delta }$ is a constant, which is used to determine whether the step size of the missing modal signal sample value should be increased or decreased during each iteration. Similarly, the expression for is shown in Eq. (4):

Then, the difference of the gradient vector $G={\left[G\left(0\right),G\left(1\right),...,G\left(N\right)\right]}^T$ is estimated, where the coordinate of this gradient vector is considered as a constant when it is on a normal sample of the received modal signal, so the value of the coordinate of this gradient vector is 0. Conversely, if the coordinate of the gradient vector is positioned on the sample point of the missing modal signal, it is solved as the difference of the signal sparsity. Then, during the $i+1$th iteration, the coordinates of the gradient vector are shown in Eq. (5):

And the value of the signal $y$ is corrected by the gradient vector $G$ during the continuous iteration, the expression is shown in Eq. (6):

where, $\mu$ is used to describe the difference step at each iteration and is assigned the value $\mu =2\mathrm{\Delta }$. Iteratively, the above steps are performed and the missing modal sampling values eventually converge to a sampling point in the modal domain with minimum sparsity; meanwhile, the performance of the algorithm depends on the parameter $\mathrm{\Delta }$.

When a sample point $y\left(n_0\right)$ is a missing modal sample signal, the sparsity of the sample point varies with increasing step $\mathrm{\Delta }$ or decreasing step $\mathrm{\Delta }$ of the signal $y\left(n_0\right)$ at the sample point [16]. Assuming that the exact value of the missing mode has been obtained, the form of the sparse signal in the modal domain can be expressed as Eq. (7):

Since the gradient vector is estimated using the difference of sparsity, the gradient with ${\mathcal{l}}_1$-paradigm is constant under conditions close to the optimality of the algorithm, so it cannot be solved with more accuracy than the step size $\mathrm{\Delta }$. Then when the initial step size is too large, the method is not accurate enough. If the initial step size is small, it leads to a large number of iterations, which results in inefficiency and wasted time. The best approach is the adaptive step size approach, where the step size is increased when the sparsity does not converge to a minimal point. The step size is reduced when the sparsity converges to a minima. That is, GDA recovers the missing modes as shown in Fig. 2.

Fig. 2GDA restoration process of missing modes

3.2. Vortex electromagnetic wave radar super-resolution direction finding technique based on LMMSE for missing mode recovery

The results of GDA-based missing mode recovery are affected by the number of valid modes obtained, and if the number of obtained modes is small, the recovery results will be worse. In view of this, the study will recover the missing modes based on Linear minimum mean square error (LMMSE). First, a preliminary spectral estimation is performed based on the obtained effective modal data vector to obtain a coarse spectrum. Then, a linear relationship between the effective and missing mode vectors is derived. Finally, the linear transformation of the valid modes is used to estimate the missing modes.

Two methods, IAA and SLIM, are used to obtain better orientation spectra with less OAM. On this basis, coarse spectral estimation is performed using these two methods, followed by linear estimation. This leads to modal recovery algorithms called Missing Modes Iterative Adaptive Apporoach (MMIAA) based algorithm, Missing Modes Sparse Learning via Iterative Minimization (MMSLIM) algorithm. In particular, the process of the MMIAA recovery algorithm is shown in Fig. 3.

Fig. 3Process of MMIAA recovery algorithm

As can be seen in Fig. 3, the iterative process needs to be repeated in the MMIAA recovery algorithm until the algorithm converges. Similarly, the process of the MMSLIM recovery algorithm is similar to Fig. 3.

To estimate the coarse spectrum using IAA in the effective mode, the azimuthal domain needs to be first decomposed into equally spaced $K$ grid points, assuming ${\phi }_k$, and that $k=\mathrm{1,2},...,K$ is the target scattering coefficient corresponding to that point in this azimuthal domain; usually, $K$ will take a larger value to obtain better azimuthal resolution [17]. Where the complete modal domain signal expression is shown in Eq. (8):

where, $\sigma$ is the target scattering coefficient and $\eta$ is meant to be the noise signal at the different modes [18]. The initial spectral estimation of the modal data can generally be performed using weighted least squares, then the spectral estimation at ${\phi }_k$ is able to be converted to Eq. (9):

Solving for the partial derivatives of $\sigma$ enables a weighted least squares estimate to be obtained, with the expression shown in Eq. (10):

By means of matrix inverse derivation, it is possible to obtain the Eq. (11):

Considering that all meshes require repeated calculations for $Q_g^{-1}$, to circumvent this phenomenon, Eq. (11) is substituted into Eq. (10) so that the number of times $R_g^{-1}$ needs to calculate the matrix inverse during each iteration is only one; and the expression for each iteration of $\sigma \left({\phi }_k\right)$ is obtained, as shown in Eq. (12):

Because the complex amplitude at each grid point must be known in order to perform the calculation of $R_g^{-1}$, the $R_g$ can be assigned as a unit matrix when the initialization is performed. During subsequent iterations, the $\sigma$ estimated in the previous iteration is used continuously to calculate $R_g^{-1}$. If the difference between the results obtained from two adjacent iterations is below a certain threshold, then the iteration is terminated [19].

Once the coarse spectrum has been estimated from the obtained modal data, the missing modal data can be recovered from the coarse spectrum, i.e. by linear transformation of $y_g$. The expression is shown in Eq. (13):

Therefore, it is possible to estimate $y_m$ using linear minimization of mean square error, and the expression of mean square error of $y_m$ is shown in Eq. (14):

The equality sign in Eq. (14) can hold when $T=R_{mg}{R}_g^{-1}$. Then the root mean square error of $y_m$ can be optimally estimated at this time, and the expression is shown in Eq. (15):

Eq. (15) shows that when the posterior $\sigma \left({\phi }_k\right)$ is calculated, $P_k$ can be found, and then multiplied with the numerator of the iterative equation, $y_m$ can be calculated [20].

4.1. Simulation results of missing mode recovery based on ASSGD and LMMSE

Firstly, the missing mode recovery results based on ASSGD are analysed, and the missing modes are recovered using the gradient descent method, and simulation experiments are carried out. The computer system used in the experiment was Windows 8, and the programming tool was Python. The parameters of the simulation include: 10 GHz vortex EM signal frequency, 4$\lambda$ UCA array element diameter, the number of emitted OAM modes set to [–25, 25], a total of 50 OAM modes, and a signal-to-noise ratio of 15 dB. The original signal is generated by setting two ideal object scattering points on 50 and 70. Of the 50 modes, 20 were lost randomly, i.e., the mode-missing ratio was 40 %. Generally, with missing modes, there are many zero values in the received signal and the gradient descent method to recover the missing modes is shown in Fig. 4.

The experimental results show that GDA is able to recover the sample values of the missing modes very well. Their orientation spectra were obtained by performing FFT calculations on the original fully modal sample signal, the received signal in the missing mode, and the sample signal after recovering the mode, respectively. The results are shown specifically in Fig. 5.

Fig. 4Comparison of sample values of restored mode and original mode

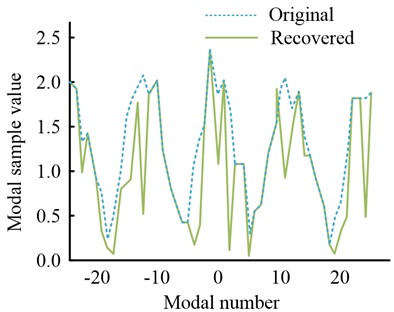
a) All modal samples

b) Missing modal samples

Fig. 5Normalized azimuth spectrum of sample signal under three modes

a) Normalized azimuth spectrum of sample signal in complete mode

b) Normalized azimuth spectrum of sample signal in missing mode

c) Normalized azimuth spectrum of sample signal under recovery mode

Fig. 5 shows that the missing mode significantly affects the azimuthal spectrum, increasing the number of partials in the azimuthal spectrum significantly, and if the missing mode is restored, the effect of the partials is somewhat diminished.

The LMMSE-based missing modes are then simulated and analysed by first generating the vortex radar echoes of the missing modes and simulating them. The parameter settings during the simulation are the same as in Section 1, and out of 50 modes, 25 modes are lost randomly, i.e., the mode missing ratio is 50 %. At the same time, the number of missing modes, the original signal and the actual received signal with the missing modal data are significantly different. Using the MMIAA and MMSLIM algorithms, the sample data of the received missing modal signal was recovered and the results are shown in Fig. 6.

Fig. 6Comparison of restored mode and original mode sample values by two methods

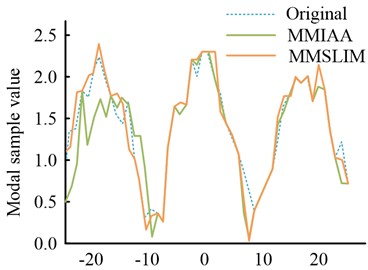
a) All modal samples data

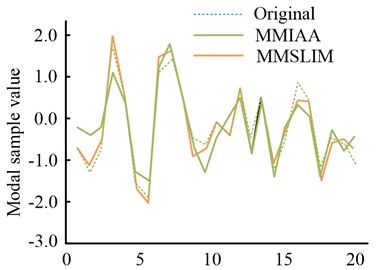
b) Missing modal samples will restore sample data

Fig. 7Normalized azimuth spectrum of sample signal in four cases

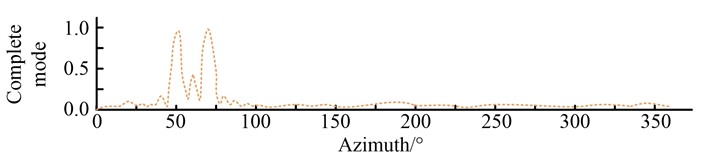
a) Normalized azimuth spectrum of sample signal in complete mode

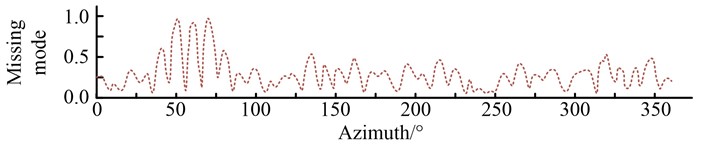
b) Normalized azimuth spectrum of sample signal in missing mode

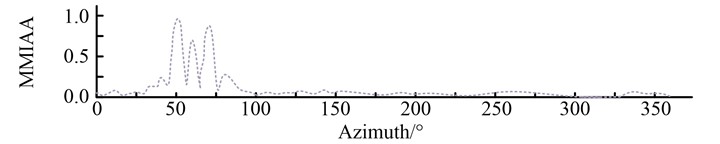
c) Normalized azimuth spectrum of sample signal under recovery mode

d) Normalized azimuth spectrum of sample signal under recovery mode

As can clearly be observed in Fig. 6, both methods recover the sample values of the missing modes very well at a modal deficiency rate of 50 %. And the MMSLIM algorithm outperforms the MMIAA algorithm in that the former recovers the sample values of the modes that are essentially identical to the values of the original signal.

The orientation spectrum of the original fully modal sample signal, the received signal in the missing mode, the modal sample signal after MMIAA recovery, and the modal signal after MMSLIM recovery were solved using the FFT method, and the results are shown in Fig. 7.

It can be found that the missing mode has a significant effect on the formation of the azimuthal spectrum. After the missing modes were recovered using MMIAA and MMSLIM, the side flaps of the azimuthal spectrum were significantly reduced compared to the missing modes, and the resulting azimuthal spectrum was basically the same as that of the full modal sample.

4.2. Algorithm performance analysis

Simulation experiments of the three algorithms under study are carried out for snail-rotation radar in a mode-deficient environment. The differences in the experimental results of the three algorithms under different simulation conditions are evaluated using metrics such as root mean square error of recovery accuracy, root mean square error of spectral estimation super-resolution after recovering the modalities, and combined with Monte Carlo random experiments to estimate RMSE and RMSE of recovery accuracy.

Simulation tests were carried out for ASSGD, MMIAA and MMSLIM to compare the effectiveness of the three methods in the case of modal deficiencies. The root-mean-square error of recovery accuracy, the root-mean-square error metric of super-resolution of spectral estimation after recovering the modalities are used for evaluation, and the RMSE and RMSE of recovery accuracy are estimated in conjunction with Monte Carlo random experiments.

First, the recovery accuracy of the ASSGD, MMIAA and MMSLIM algorithms is compared for different modal deficit ratios. The main simulation parameters are set in the same way as in Section 1. Also, from the 50 modes, a specific proportion of modes is selected and simulated for the case of missing modes. The modal missing ratios were set to 0-0.9, and the number of Monte Carlo experiments at all missing ratios was 100. The missing modes were also recovered using three algorithms and RMSE analysis was performed on the results recovered by the three algorithms and the results are shown in Fig. 8.

Fig. 8Recovery error of three algorithms under different modal loss ratios

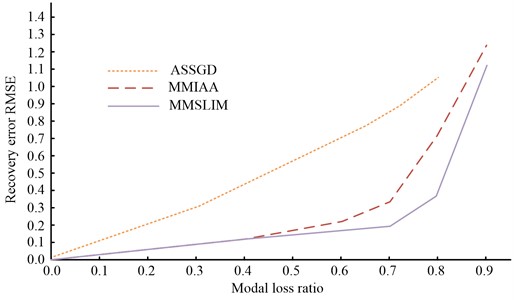
Fig. 8 gives the missing ratios of the three methods for various modal missing ratios. It can be seen that the recovery accuracy of all three methods decreases as the modal missing ratio increases. In the case of obtaining the full modal sample, no recovery is required and the error is 0. The high recovery accuracy of MMSLIM is MMSLIM, MMIAA and ASSGD in descending order. at a modal missing ratio of 0.7, the recovery error RMSE for MMSLIM, MMIAA and ASSGD are 0.16, 0.31 and 0.82 respectively. while at a model missing ratio of 0.9, ASSGD was unable to recover the missing modal data.

Based on this, the study proposes to use three modal recovery methods. The vortex radar azimuth spectrum is calculated using the radar echo data under modal deficiency and the echo data after modal recovery, respectively. The mathematical model of the vortex radar azimuth spectrum is also established using the RMSE of the azimuth angle to the original target as the evaluation criterion. To address the problem that the accuracy of the above method will drop significantly after the modal loss ratio reaches 0.7, the study set the modal loss ratio between 0 and 0.7, 100 Monte Carlo random trials, each round of experiments set two random targets with azimuth interval of 10, the signal-to-noise ratio is 15dB, the simulation results are shown in Fig. 9.

Fig. 9Estimated RMSE of target orientation after modal restoration by three algorithms under different modal loss ratios

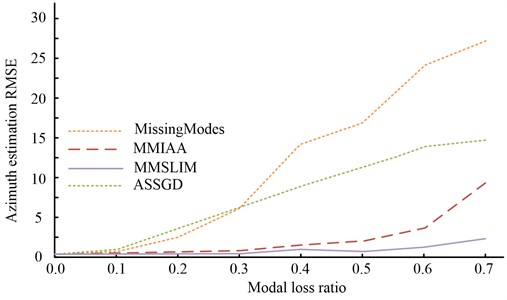
In Fig. 9, it can be seen that the modal loss has a significant impact on the directional accuracy of the vortex radar, while the recovered directional accuracy is improved to some extent by using various modal recovery methods. The difference between the directional accuracy recovered by the MMSLIM method and that recovered by the MMSLIM method is not significant. The recovery accuracies of the three algorithms were then calculated for different signal-to-noise ratios. The aim of this experiment is to evaluate the RMSE of the various methods for vortex radar recovery at different S/N ratios. the total number of OAM modes is set to 50, the modal loss ratio is set to 0.7, the S/N ratio is increased by 5 dB for every 5 dB from –5 to 30 dB, and the number of Monte Carlo experiments at each S/N ratio is 100.

Fig. 10Recovery RMSE of three algorithms under different SNR

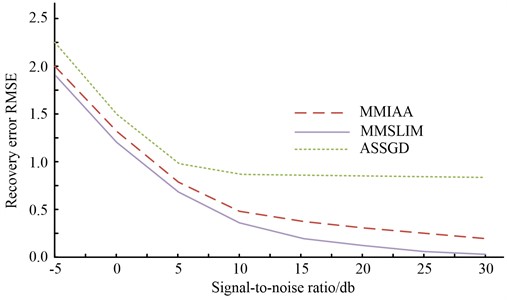
The simulation results are shown in Fig. 10, where, overall, the recovery error of each method decreases as the signal-to-noise ratio increases, and its accuracy improves. Furthermore, when the modal missing ratio is 0.7, each method can recover the missing modes at different levels, with the MMSLIM algorithm having the best results. Similar to the above simulation tests, the accuracy of the target orientation estimation after modal recovery was simulated by setting the modal missing ratio to 0.7 at –5 to 30 dB. The Monte Carlo tests were repeated 100 times for different signal-to-noise ratios, with randomised azimuths for each test subject.

Fig. 11Estimation of target bearing RMSE after modal recovery under different signal-to-noise ratios

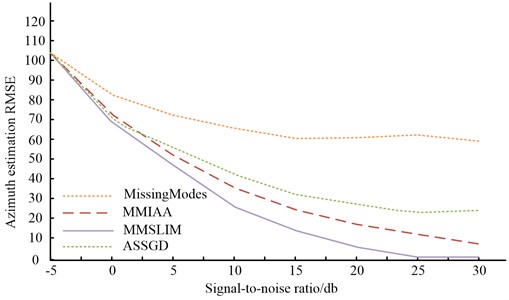
From the simulation results in Fig. 11, it can be seen that the accuracy of the azimuth estimation continues to increase as the signal-to-noise ratio continues to increase, but the RMSE through modal recovery is better than the accuracy in the missing modal case. When the S/N ratio is at [–5, 10] dB, the overall data quality is average. And at reaching 15 dB or more, the conditions of the algorithm can be met and the curve becomes smoother. The accuracy of the three algorithms was analyzed, and the results are shown in Fig. 12.

Fig. 12Accuracy analysis of three algorithms

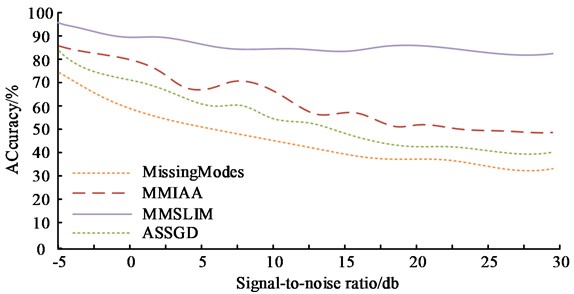
From Fig. 12, it can be seen that as the signal-to-noise ratio continues to increase, the prediction accuracy of the three algorithms decreases. However, overall, the prediction accuracy of the three algorithms is MMSLIM, MMIAA, and ASSGD from high to low.

The results of the above simulations show that the three algorithms are in the order of MMSLIM, MMIAA and ASSGD in terms of the recovery accuracy of the missing modes, the accuracy of the recovered azimuth resolution and the complexity of the algorithm, while the results of the three algorithms are in the order of ASSGD, MMIAA and MMSLIM in terms of the recovered azimuth spectral parametrization level.

The analysis results of the three algorithms are shown in Table 1.