Influence of a nonlinear asymmetric shock absorber on vibration of a bus subjected to harmonic excitation

Tran, Huu Nhan; E. Gunawan, Fergyanto; Pham, Ngoc Dai

doi:10.21595/jve.2023.23404

Journal of Vibroengineering

Browse Journal

Submit article

Published: 25 November 2023

Check for updates

Influence of a nonlinear asymmetric shock absorber on vibration of a bus subjected to harmonic excitation

Huu Nhan Tran¹

Fergyanto E. Gunawan²

Ngoc Dai Pham³

^{1, 3}culty of Transportation Engineering, Ho Chi Minh City University of Technology (HCMUT), Vietnam National University, 268 Ly Thuong Kiet Street, District 10, Ho Chi Minh City, Vietnam

²Industrial Engineering Department, Bina Nusantara University, Jakarta, 11480, Indonesia

Corresponding Author:

Huu Nhan Tran

Cite the article Download PDF

Downloads 79

CrossRef Citations 1

Abstract

The main focus of paper is to get full understanding of four different types of shock absorbers characteristics and their effects on the vertical evaluation indexes of a bus subjected to harmonic excitation. The quarter car with two degree of freedom (2DOF) model was employed to calculate the vertical evaluation indexes. The bus is assumed to travel at a constant velocity on a road surface with a profile following a sinusoidal function. The four types of the shock absorber are Linear Symmetric (LS), Nonlinear Symmetric (NS), Linear Asymmetric (LA), and Nonlinear Asymmetric (NA). As for the LS type, the damping force is a linear function of the relative velocity, and the damping force is symmetric for the conditions of the positive and negative relative velocities. Same as for the LA type, it means that the damping force is linear, however it is asymmetric and differentiated according to the suspension state of stroke (compression or extension). As for the NS type, the damping force function is symmetric, nonlinear, differentiated according to the magnitude of the relative velocity. As for the last NA type, the damping force function is also nonlinear and differentiated according to the magnitude of the relative velocity, but it is also asymmetric. The obtained evaluation indexes of the relative displacement of the bus suspension, acceleration of the bus body, and the dynamic tire load within the frequency range of 0 and 25 (Hz), the common frequency range of the bus in operations. The results suggest that the NA shock absorber type is more effective in reducing the suspension dynamic deflection stroke, improving the road holding and maintaining the ride comfort. The systematic assessments of the shock absorber characteristics should guide interested readers in selecting the most appropriate damping coefficient.

Influence of a nonlinear asymmetric shock absorber on vibration of a bus subjected to harmonic excitation

Highlights

At the peak performance, the nonlinear shock absorber types have 15% lower MTDL than those of the linear shock absorber types.
Both nonlinear shock absorbers greatly reduce the GSDDS.
Both linear shock absorbers nearly have similar GSDDS.
Nonlinear Asymmetric type achieves the best performance in both the maximum and the average BVA.

1. Introduction

With the increasing requirements, especially for the ride comfort of buses, which are manufactured and assembled in Vietnam. Bus ride comfort was carried out by the multibody dynamic model to help the bus designers and manufacturers in order to improve and harmonize oscillatory comfort on the whole vehicle platform [1]. The oscillatory model with 10DOF was employed to investigate the effects of bus vibrations on the comfort for the space of a driver, passenger in the middle part of the bus and passenger in the rear overhang [2]. The determination of suspension parameters is very important, because it is directly related to ride comfort, safety and road holding during the operation of vehicles. The evaluation indexes of the ride comfort, workability, and operational safety of the bus suspension system were studied under the random excitation, with the change of the stiffness and damping values in the investigated domain [3, 4]. It shows that shock absorbers represent a critical element of a suspension, in order to better understand the influence of damping parameters on ride comfort of vehicles, many studies have been carried out [5, 6]. The multibody model of a larger bus was employed, in which a dynamic model for the MR (magnetic-rheological) damper was developed, a comparison to the traditional passive damper model showed the improvement [5]. The 2DOF quarter car model with LA shock absorber, in which the damping ratio value changing with the stroke was used to analyze the vertical dynamics of an electric vehicle. The road profile was in type of triangular shape according to GB/T 4970-2009 standard, the vehicle moves over the bump with different speeds [6]. The influence of LA shock absorber on the vehicle's ride comfort, was studied with the single bump effect, by using the 2DOF quarter car and the 4DOF half car models [7]. The influence of LA shock absorber under the effect of the harmonic excitation was studied to improve the vehicle's ride comfort, by the 2 DOF quarter car model [8]. Recently, an investigation of a bus’s ride comfort with the two types of LS and LA shock absorbers was carried out, in which the quarter car model was employed, subjected under transient and random road excitations [9].

In Vietnam’s practice, the types of shock absorbers have been recently used in the design and manufacture of buses are of symmetric/asymmetric and linear/nonlinear ones. This paper is conducted to get full understanding of the influences of the 4 types of common shock absorbers’ characteristics on the bus vibration. The vibration evaluation indexes for a typical bus have been specifically identified corresponding to each type of shock absorber characteristic, in which the initial damping coefficient $c_{0}$ is chosen as the same for all 4 types of shock absorbers. The evaluation indexes in terms of ride comfort, suspension working space, and road holding are determined under the excitation of the harmonic function. The obtained results are presented and analyzed systematically to help understand the nature of the influences of 4 common types of shock absorbers characteristics on the typical bus vertical dynamic evaluation indexes in the frequency domain. Especially, the peak values of the obtained gain responses at the corresponding resonance values of the natural frequencies of the suspension system and the tire, respectively. The type of NA shock absorber gives the best results in improving suspension performance, road holding, and maintaining ride comfort for the buses, which are being designed and manufactured in Vietnam.

2. Research method

2.1. Simulation model

This research intends to evaluate four types of shock absorbers in the suspension system and their effects on ride comfort, suspension working space and road holding of the bus. We develop a bus suspension model, compute the responses of acceleration, relative displacement and tire dynamic load (TDL), and establish its characteristics to understand the four types of shock absorbers that affect the bus vertical dynamic evaluation indexes. The bus model is simplified as a system consisting of masses, springs, and a damper as shown in Fig. 1.

Fig. 1The quarter car 2DOF model [10]

The symbols, and the meanings of the quarter car 2DOF model parameters, are given in Table 1.

Table 1The quarter car 2DOF model parameters

Symbol	Description	Value
$m_{s}$	Sprung mass [kg]	2000
$m_{u}$	Un-sprung mass [kg]	250
$k_{s}$	Suspension spring stiffness [N/m]	8×10⁴
$c_{0}$	Initial damping coefficient [Ns/m]	7500
$k_{t}$	Tire stiffness [N/m]	1×10⁶
$x_{s}$	Vertical displacement of the sprung mass [m]	–
$x_{u}$	Vertical displacement of the un-sprung mass [m]	–
$Y$	Road excitation [m]	–

In the Fig. 1, the bus body is denoted by the sprung mass $m_{s}$ , and the suspension system connects the un-sprung mass $m_{u}$ . The displacements of the sprung and un-sprung masses are denoted by $x_{s}$ and $x_{u}$ , respectively. The suspension consists of a spring $k_{s}$ and an equivalent damping coefficient $c_{e q}$ , provides support to the bus body. The bus is assumed to travel at a constant speed $v$ on a road surface with a road profile $y$ . The stiffness between the un-sprung mass and the road is the tire stiffness denoted by $k_{t}$ . The sprung mass is 2000 (kg), and the un-sprung mass is 250 (kg). The spring stiffness $k_{s}$ is 8.10⁴ (N/m), corresponding to the natural frequency of the bus suspension system of about 1 (Hz) [1]. The tire stiffness $k_{t}$ is 1.10⁶(N/m).

The set of differential equations describing the 2DOF vertical dynamic model, is written in matrix form as shown in Eq. (1) as, [10]:

1

[m] \ddot{X} + [c] \dot{X} + [k] X = [F],

where, the matrices included in the general dynamic equation are presented as:

X = [\begin{array}{l} x_{u} \\ x_{s} \end{array}], \dot{X} = [\begin{array}{l} {\dot{x}}_{u} \\ {\dot{x}}_{s} \end{array}], \ddot{X} = [\begin{array}{l} {\ddot{x}}_{u} \\ {\ddot{x}}_{s} \end{array}],

[m] = [\begin{matrix} m_{u} & 0 \\ 0 & m_{s} \end{matrix}], [k] = [\begin{matrix} k_{s} + k_{t} & - k_{s} \\ - k_{s} & k_{s} \end{matrix}], [c] = [\begin{matrix} c_{e q} & - c_{e q} \\ - c_{e q} & c_{e q} \end{matrix}], [F] = [\begin{matrix} k_{t} y \\ 0 \end{matrix}] .

The variables $\dot{x}$ and $\ddot{x}$ denote the velocity and acceleration. The subscripts $t$ and $s$ represent the tire and suspension, respectively. In addition, we introduce the shock absorber force $F_{c}$ , which is linearly related to the relative velocity of the suspension system. The force is expressed by:

2

F_{c} = c_{e q} d z,

where $d z$ is the relative velocity of the suspension, defined by:

3

d z = {\dot{x}}_{s} - {\dot{x}}_{u} .

The equivalent damping coefficient $c_{e q}$ is related to the damping ratio $ξ$ by $c_{e q} = 2 ξ \sqrt{m_{s} k_{s}}$ where the damping ratio value is in range of 0.2-0.4, [11]. In the present study, we focus on four different damping characteristics. The initial value of the damping coefficient is $c_{0} =$ 7500 (Ns/m), corresponding to $ξ =$ 0.3.

2.2. Harmonic excitation

We assume the bus is moving at a constant velocity v on the surface of a road whose profile follows a sinusoidal harmonic function of time $t$ , as in Eq. (4):

4

y = \{\begin{array}{l} \frac{d_{2}}{2} s i n (\frac{2 π v}{d_{1}} t), & t \geq 0, \\ 0, & t < 0 . \end{array}

The considered road profile is characterized by the road bump length $d_{1}$ , the road bump height $d_{2}$ , and the velocity $v$ , see Fig. 2. The road bump is 1 (m) in length and 0.005 (m) in height. The velocity $v$ is chosen to be in range of 1-100 (km/h) corresponding to the frequency of excitation in the range of 0.28-27.78 (Hz), determined by Eq. (4).

Fig. 2The road profile described by the sinusoidal harmonic function [10]

2.3. The four types of shock absorbers

Four types of shock absorbers are investigated. The parameters of shock absorber models are given in Table 2.

Table 2Shock absorber model parameters

Symbol	Description	Value
$c_{0}$	Initial damping coefficient [Ns/m]	7500
$d z_{c}$	Knee-point [m/s]	0.05
$κ$	Slope of low-speed damping coefficient	2
$λ$	Slope of high-speed damping coefficient	1
$e_{D}$	Asymmetric coefficient	0.4

The first case is the Linear Symmetric (LS) shock absorber. In the LS type, the generated damping force is proportional to the relative velocity $d z$ of the suspension system. The damping coefficient is fixed at $c_{0} =$ 7500 (N.s/m).

The second case is called Nonlinear Symmetric (NS) shock absorber. This type is characterized by a knee point $d z_{c} =$ 0.05 (m/s), which separates the shock absorber response into two domains: low and high speeds. The damping force is governed by $κ$ parameter at the low speed and by $λ$ parameter at high speed. For the NS type, the shock absorber force follows the following formulas:

5

F_{c} = \{\begin{array}{l} κ c_{0} d z, & |d z| \leq d z_{c}, \\ c_{0} [λ d z - (κ - λ) d z_{c}], & \begin{array}{l} d z < 0 \end{array}, \begin{array}{l} \begin{array}{l} |d z| > d z_{c} \end{array} \end{array}, \\ c_{0} [λ d z + (κ - λ) d z_{c}], & \begin{array}{l} d z > 0 \end{array}, \begin{array}{l} \begin{array}{l} d z > d z_{c} \end{array} \end{array} . \end{array}

We choose $κ = 2$ and $λ = 1$ , suggesting the damping strength at the low speed is twice as big as at high speed. The damping coefficient in the high-speed region is $c_{0}$ .

The third case is Linear Asymmetric (LA) shock absorber. The shock absorber force follows the formula:

6

F_{c} = \{\begin{array}{l} (1 - e_{D}) c_{0} d z, & \begin{array}{l} d z < 0, \end{array} \\ (1 + e_{D}) c_{0} d z, & \begin{array}{l} d z > 0 \end{array} . \end{array}

The asymmetric coefficient $e_{D}$ is taken as 0.4 [12], corresponding to the ratio of the compression and extension strokes of 30 to 70. Initially, the equivalent damping coefficient $c_{e q}$ is taken to be equal to the initial one c₀, when the relative velocity, $d z =$ 0.

Finally, the fourth case is Nonlinear Asymmetric (NA) shock absorber. To some extent, the case is a combination of Case 2 and Case 3. The damping force changes proportionally but asymmetrically with the coefficient $e_{D}$ . The slope of the damping force is altered at the knee-point value $d z_{c}$ with the coefficients $κ$ and $λ$ . Similarly, initially, when $d z =$ 0, the equivalent damping coefficient $c_{e q}$ equals to $c_{0}$ . Analytically, the damping force follows the following composite functions:

7

F_{c} = \{\begin{array}{l} κ c_{0} d z (1 - e_{D}), \begin{array}{l} \begin{array}{l} \begin{array}{l} d z < 0 \end{array}, \begin{array}{l} \begin{array}{l} |d z| \leq d z_{c} \end{array} \end{array} \end{array} \end{array}, \\ (1 - e_{D}) c_{0} [λ d z - (κ - λ) d z_{c}], \begin{array}{l}  \end{array} \begin{array}{l} d z < 0 \end{array}, \begin{array}{l} \begin{array}{l} |d z| > d z_{c} \end{array} \end{array}, \\ κ (1 + e_{D}) c_{0} d z, \begin{array}{l} \begin{array}{l} d z > 0 \end{array}, \begin{array}{l} \begin{array}{l} d z \leq d z_{c} \end{array} \end{array} \end{array}, \\ (1 + e_{D}) c_{0} [λ d z + (κ - λ) d z_{c}], \begin{array}{l}  \end{array} \begin{array}{l} d z > 0 \end{array}, \begin{array}{l} \begin{array}{l} d z > d z_{c} . \end{array} \end{array} \end{array}

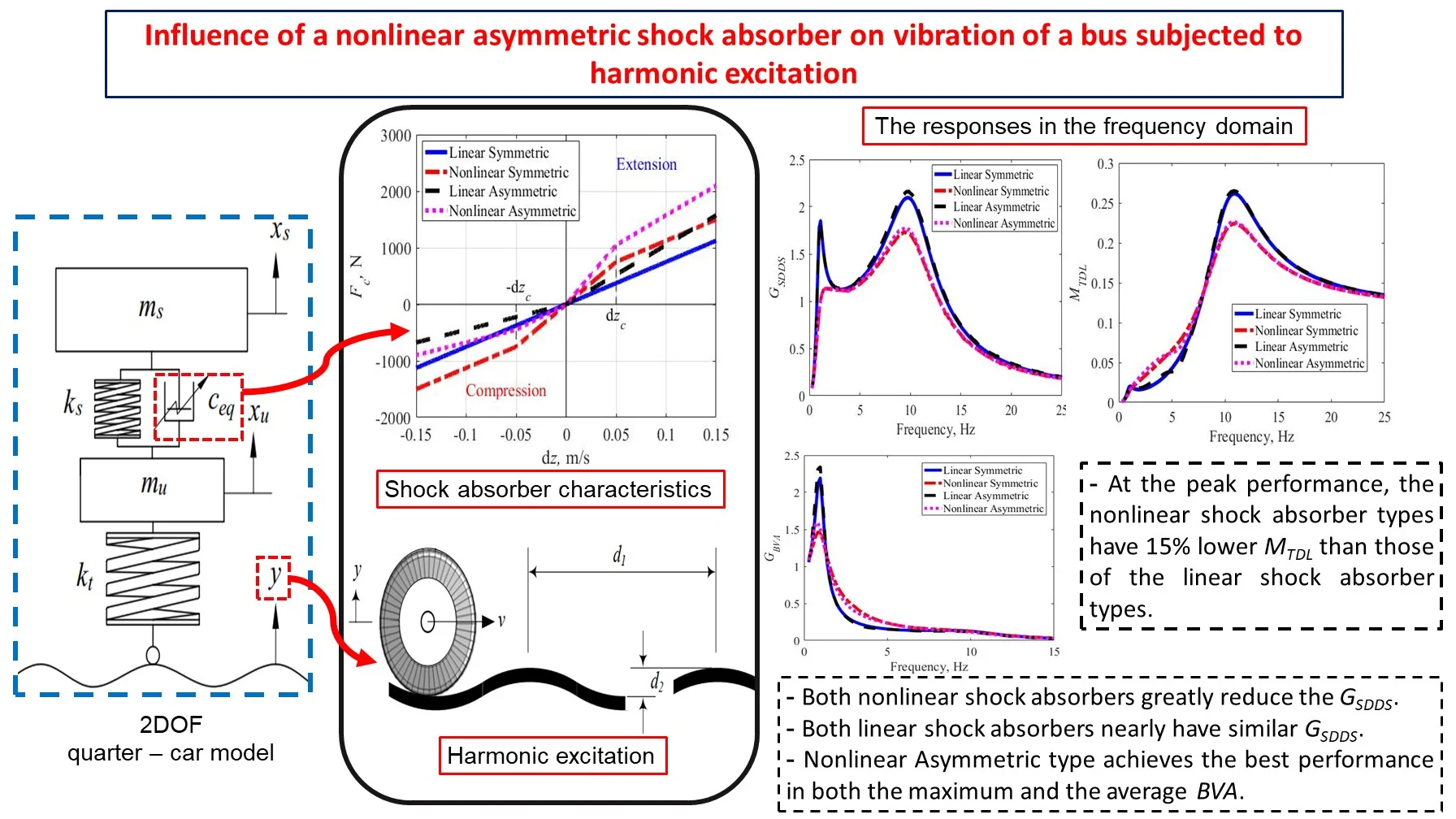
In Fig. 3, a comparison is graphically made for the four types of shock absorbers. The relative velocity $d z$ is plotted against the shock absorber force $F_{c}$ . For the first case, Linear Symmetric shock absorber, the damping force increases linearly with the velocity. The linear relationship is also present for the third model but with a knee-point at $d z =$ 0, resulting in a bilinear curve. The second and fourth models have three knee points at $d z = - d z_{c}$ , $d z =$ 0, and $d z = d z_{c}$ , breaking down the velocity range into four domains, namely, $d z = < - d z_{c}$ , $- d z_{c} \leq d z <$ 0, $0 < d z \leq d z_{c}$ , and $d z > d z_{c}$ . In each domain, the damping force is proportional to the relative velocity of the suspension.

Fig. 3The relationship between the damping force Fc and the relative velocity dz for the four types of shock absorbers

2.4. Evaluation indexes

Calculations are performed for each value of applied excitation frequency. The parameters of Suspension Dynamic Deflection (SDD), acceleration of the sprung mass namely Body Vibration Acceleration (BVA), and Tire Dynamic Load (TDL) are determined in the time domain, when in steady-state of the harmonic responses with the same frequency as the applied excitation frequency. The amplitude values of the obtained results in the time domain are determined at steady-state. Then, the evaluation indexes are determined in the frequency domain with the frequency range of 0-25 (Hz), a normal range for the vehicle operations [10]. Especially at the resonance values corresponding to each type of damper, can be characterized most meaningfully and systematically.

2.4.1. Gain response of SDD

The relative displacement of the suspension to evaluate the Suspension Dynamic Deflection (SDD). The gain response of maximum and minimum relative displacement are defined as the corresponding ratio of the maximum and minimum relative displacements to the amplitude of the road excitation, $d_{2}$ , [10], following the Eq. (8), and Eq. (9), respectively:

8

G_{S D D m a x} = \frac{m a x (x_{s} - x_{u})}{0.5 d_{2}},

9

G_{S D D m i n} = \frac{m i n (x_{s} - x_{u})}{0.5 d_{2}} .

It is easy to see that the working stroke of the suspension system with asymmetric shock absorber is asymmetric around the initial equilibrium position. To be able to compare the Suspension Dynamic Deflection Stroke (SDDS) parameter of different types of shock absorbers, the gain response of SDDS is determined by Eq. (10):

10

G_{S D D S} = \frac{m a x (x_{s} - x_{u}) - m i n (x_{s} - x_{u})}{d_{2}} .

2.4.2. Gain response of BVA

The gain response of the Body Vibration Acceleration (BVA), $G_{B V A}$ is defined as the ratio of the value of the sprung mass acceleration amplitude variation over time to the applied excitation acceleration amplitude. Mathematically, the $G_{B V A}$ is calculated by Eq. (11):

11

G_{B V A} = \frac{m a x ({\ddot{x}}_{s})}{0.5 d_{2} {(\frac{2 π v}{d_{1}})}^{2}} .

2.4.3. Tire dynamic load - TDL

The maximum tire dynamic load $M_{T D L}$ is defined as the ratio of the maximum dynamic force applied to the tire to the static reaction load [6]. The $M_{T D L}$ is computed by Eq. (12):

12

M_{T D L} = \frac{m a x [k_{t} (x_{u} - y)]}{(m_{s} + m_{u}) g} .

2.4.4. Calculation flowchart

For each type of the shock absorber, calculations are performed for each frequency of the harmonic excitation, the corresponding harmonic responses of SDD, BVA and TDL in the time domain are determined. And then, the corresponding amplitudes of these obtained steady-state harmonic responses are determined. Therefore, for each frequency of applied excitation, the evaluation indexes of SDD, BVA and TDL are determined by the Eqs. (8)-(12). Next, do the same calculation for the next remaining excitation frequency values in the observed domain. The evaluation indexes are identified and analyzed in the observed frequency domain. The calculation flowchart is shown in Fig. 4.

3. Results and discussions

3.1. Gain response of SDD

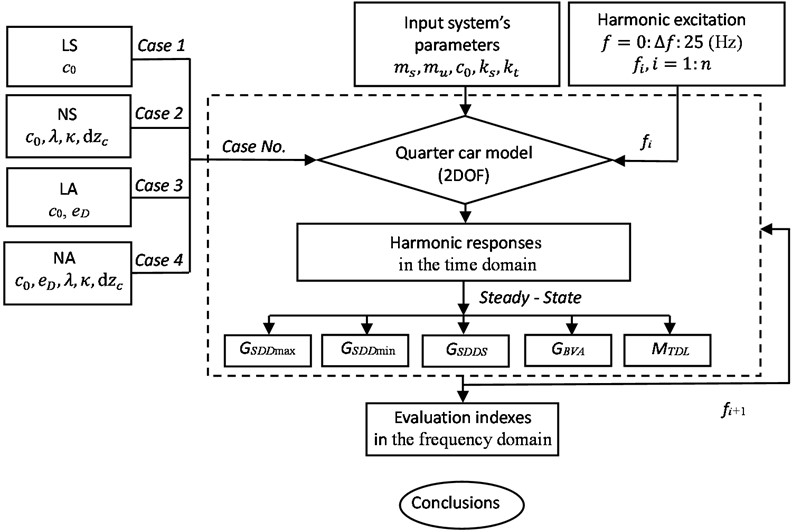
The gain responses of maximum relative displacement $G_{S D D m a x}$ are calculated by Eq. (8) in the frequency domain, for the two cases of LS and NS, Fig. 5. Both of the cases, the obtained $G_{S D D m a x}$ are symmetrical to the zero frequency in the domain. The responses have two peaks associated with the two resonances of the system. The first is the suspension’s natural frequency $f_{n 1}$ of about 1 (Hz), and the second is the tire’s natural frequency $f_{n 2}$ of about 10 (Hz). It can be seen that the first peak of the NS shock absorber, which occurs at a low frequency, is lower than that of the LS shock absorber. The phenomenon happens because the NS case has a more significant damping coefficient when $|d z| < d z_{c}$ , corresponding to the low-frequency domain. In addition, the NS shock absorber also has a lower $G_{S D D m a x}$ at the second peak. The gains are lower about 33 % at the first peak and 17 % at the second peak. On average, the $G_{S D D m a x}$ of the NS shock absorber is lower by about 12 %.

Fig. 4The calculation flowchart

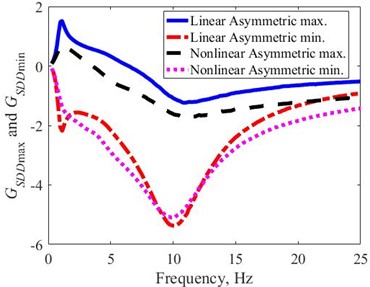
As for the cases of asymmetric shock absorbers, the obtained $G_{S D D m a x}$ and $G_{S D D m i n}$ are calculated by the Eqs. (8-9), in the frequency domain, Fig. 6. Unlike the previous cases, the gain responses are not symmetric to the zero-frequency axis. In this case, the damping coefficient value depends on the shock absorber states, namely, tension or compression. The value of the damping coefficient is smaller in compression than in tension. The $G_{S D D m a x}$ of the NA case is smaller about 133 % on an average than that of the LA case in the entire observed frequency domain. And, the $G_{S D D m a x}$ are lower about 56 % at the first peak and 40 % at the second peak. With the obtained $G_{S D D m i n}$ , at the 2 peaks of the LA case are lower than the NA case. However, in the frequency domain outside the 2 resonant frequencies, the $G_{S D D m i n}$ of the LA case is larger than the NA case. In the entire observed frequency range, the $G_{S D D m i n}$ of the NA case is smaller about 15 % on an average than that of the LA case. With both types of asymmetric shock absorbers, the obtained $G_{S D D m a x}$ and $G_{S D D m i n}$ all have negative values, with the applied excitation greater than 5 (Hz), which indicates that the suspension system is working mostly in the state under compression during the harmonic applied excitation. Due to the asymmetrical characteristic of the shock absorbers, the suspensions move up and down around a position lower than their initial equilibrium position. Therefore, the asymmetry around the zero axis (initial equilibrium position) of the suspension relative displacement corresponds to two types of asymmetric shock absorbers, LA and NA, showing the influence of asymmetric properties of displacement.

Fig. 5The GSDDmax of the LS and NS shock absorbers in the frequency domain

Fig. 6The GSDDmax and GSDDmin of the LA and NA shock absorbers in the frequency domain

3.2. Gain response of SDDS

The obtained results of $G_{S D D S}$ for all four cases of damping characteristics are calculated by Eq. (10) and shown in the frequency domain in Fig. 7. It shows that the obtained $G_{S D D S}$ of the LS type is similar to the LA type. The obtained $G_{S D D S}$ of the NS type is identical to the NA type. Therefore, the $G_{S D D S}$ depends only on the linear or nonlinear properties of the shock absorbers, but completely independent of the asymmetrical properties. At first and second natural frequencies, the peak values of $G_{S D D S}$ with the NS type are smaller, respectively, by 33 % and 17 % compared to the LS type. With the asymmetric types of shock absorbers, the peak values of $G_{S D D S}$ with the NA type are smaller by 31 % and 18 % compared to the LA type, at the first and second natural frequencies, respectively. On average, the $G_{S D D S}$ of the NS and NA shock absorbers are lower about 12 % and 13 % than the LS and LA shock absorbers, respectively.

The obtained $G_{S D D D}$ clearly shows that the working stroke of the suspension system does not depend on the asymmetrical characteristic but only on the nonlinear characteristic of the shock absorbers. In addition, the asymmetrical characteristic of the shock absorbers only affects the equilibrium position of the suspension working stroke.

Fig. 7The GSDDS of the four shock absorbers in the frequency domain

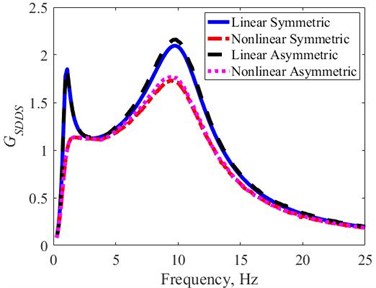
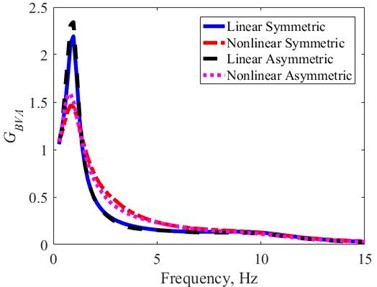
Fig. 8The GBVA of the four types of the shock absorbers in the frequency domain

3.3. Gain response of BVA

The obtained $G_{B V A}$ are calculated by Eq. (11), in the frequency domain for the four types of shock absorbers, in Fig. 8. The $G_{B V A}$ for the four types of the shock absorbers peak at the first natural frequency $f_{n 1}$ . From the peak, the $G_{B V A}$ drop quickly with the frequency. At the first natural frequency, where the peaks of the $G_{B V A}$ occur, the maximum of $G_{B V A}$ are usually in the range of 1.0-2.5, and is the range of interest in the design of the automotive suspension systems [11]. Within the range, the figure shows that the NS and NA shock absorber types have significantly lower peaks than those of LS and LA shock absorber types. However, $G_{B V A}$ of the NS and NA shock absorber types are higher in the frequency range of 3-7 (Hz). Similar to the $G_{S D D S}$ , the $G_{B V A}$ depends only on the linear or nonlinear properties of the shock absorbers, but not almost on the asymmetrical properties.

In Table 3, the characteristics of the $G_{B V A}$ of the four types of shock absorbers are presented. The table shows the maximum and the mean of the $G_{B V A}$ . The relative deviation in the case of LS shock absorber type is also explained. Compared to the LS case, the NS case has a 33 % lower the maximum of $G_{B V A}$ . The NA case has a 27 % the maximum of $G_{B V A}$ lower. However, the mean of $G_{B V A}$ is higher for the NS case (13 %) and the NA case (7 %), respectively. The nonlinear shock absorbers significantly reduce the peak of the $G_{B V A}$ . Therefore, the combination of the nonlinear and asymmetric characteristics, as in the NA case, simultaneously reduces the peak of the $G_{B V A}$ at the low frequency. And the mean of the $G_{B V A}$ in the type of NA shock absorber is not also much increased in the observed frequency range.

Table 3The maximum and mean values of GBVA for the four types of the shock absorbers

Type	Max. $G_{B V A}$	Mean $G_{B V A}$	Relative deviation (%)
Type	Max. $G_{B V A}$	Mean $G_{B V A}$	Max. $G_{B V A}$	Mean $G_{B V A}$
Linear symmetric	2.19	0.15	0	0
Nonlinear symmetric	1.47	0.17	–33	+13
Linear asymmetric	2.34	0.15	+7	0
Nonlinear asymmetric	1.59	0.16	–27	+7

3.4. Tire dynamic load – TDL

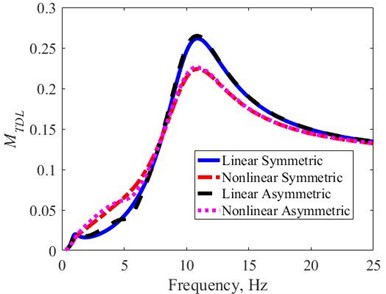
The obtained $M_{T D L}$ are calculated by Eq. (12) for the four types of shock absorbers in the frequency domain, Fig. 9. The $M_{T D L}$ reaches its peak at the second resonant frequency or the natural frequency of the tire. It is easy to see that the $M_{T D L}$ is similar for symmetric and asymmetric shock absorbers, but it is different for linear and nonlinear shock absorbers. In the other words, the $M_{T D L}$ depends only on the nonlinearity and not on the asymmetry of the shock absorbers. In the frequency range of 7-15 (Hz), the $M_{T D L}$ of linear shock absorbers are higher than those of nonlinear shock absorbers. Therefore, the nonlinear shock absorbers increase road holding because the $M_{T D L}$ has a lower value in this range of frequency domain. However, in the lower frequency range, the $M_{T D L}$ are vice versa. The peaks of the $M_{T D L}$ of the nonlinear shock absorbers are lower, about 15 %, than those of the linear shock absorbers. On average, the $M_{T D L}$ of the NS and NA shock absorbers are slightly smaller about 3 % than the LS and LA shock absorbers.

Fig. 9The MTDL of the four types of the shock absorbers in the frequency domain

4. Conclusions

In this research paper, we study the effects of the characteristics of four types of shock absorbers on the vertical dynamic behaviors of a bus. The dynamic quarter car 2DOF model is employed, subjected to harmonic excitation. The characteristics of four types of the shock absorbers, namely, Linear Symmetric, Nonlinear Symmetric, Linear Asymmetric, and Nonlinear Asymmetric are investigated. In particular, we investigate the effects shock absorber types on the evaluation indexes of the relative displacement, acceleration, and tire dynamic force. The ratio of output and input amplitudes namely the ’Gain response or Transmissibility’ represents the input-output relationships of evaluation indexes are studied and presented in the frequency domain, in the normal common range for the vehicle operations (0-20 (Hz)). The vertical dynamic behaviors, especially at the resonance region, of the bus could be characterized most meaningfully. The influences of shock absorber characteristics on the bus vibration are systematically full understanding, and the following conclusions are obtained:

1) The gain responses of the Suspension Dynamic Deflection Stroke ( $G_{S D D S}$ ) only depend on the linear or nonlinear properties of the shock absorbers, but completely independent of the asymmetrical properties. The average values of $G_{S D D S}$ of the NS and NA shock absorbers are lower about 10 % than the LS and LA shock absorbers.

2) The gain responses of the Body Vibration Acceleration ( $G_{B V A}$ ) are significantly reduced at the peaks with the types of nonlinear shock absorbers, namely NS and NA. The obtained $G_{B V A}$ also only depend on the linear or nonlinear properties and almost independent on the asymmetrical properties of the shock absorbers. In addition, the peak of the $G_{B V A}$ significantly decreases at the low frequency with the combination of the nonlinear and asymmetric characteristics of the shock absorber, namely NA, and the mean value of the $G_{B V A}$ is not also much increased in the entire vehicles’ common frequency range.

3) The maximum tire dynamic loads ( $M_{T D L}$ ) depend only on the nonlinearity and not on the asymmetry of the shock absorbers. At the peak performance, the nonlinear shock absorber types have 15 % lower $M_{T D L}$ than those of the linear shock absorber types.

References

D. Sekulić, V. Dedović, S. Rusov, A. Obradović, and S. Šalinić, “Definition and determination of the bus oscillatory comfort zones,” International Journal of Industrial Ergonomics, Vol. 53, pp. 328–339, May 2016, https://doi.org/10.1016/j.ergon.2016.04.003

Publisher
D. Sekulić, V. Dedović, S. Rusov, S. Šalinić, and A. Obradović, “Analysis of vibration effects on the comfort of intercity bus users by oscillatory model with ten degrees of freedom,” Applied Mathematical Modelling, Vol. 37, No. 18-19, pp. 8629–8644, Oct. 2013, https://doi.org/10.1016/j.apm.2013.03.060

Publisher
L. X. Long, L. Quynh, and B. Cuong, “Study on the influence of bus suspension parameters on ride comfort,” Vibroengineering PROCEDIA, Vol. 21, pp. 77–82, Dec. 2018, https://doi.org/10.21595/vp.2018.20271

Publisher
D. Sekulic and V. Dedović, “The effect of stiffness and damping of the suspension system elements on the optimisation of the vibrational behaviour of a bus,” International Journal for Traffic and Transport Engineering, Vol. 1, No. 4, pp. 231–244, 2011.

Search CrossRef
Y. Kim, S. Choi, J. Lee, W. Yoo, and J. Sohn, “Damper modeling for dynamic simulation of a large bus with MR damper,” International Journal of Automotive Technology, Vol. 12, No. 4, pp. 521–527, Aug. 2011, https://doi.org/10.1007/s12239-011-0061-5

Publisher
L. Zhao, Y. Yu, C. Zhou, S. Mao, and F. Yang, “Simulation of vertical characteristics and in-wheel motor vibration of electric vehicles with asymmetric suspension damper under road impact,” International Journal of Modelling and Simulation, 2018.

Publisher
M. Silveira, B. R. Pontes, and J. M. Balthazar, “Use of nonlinear asymmetrical shock absorber to improve comfort on passenger vehicles,” Journal of Sound and Vibration, Vol. 333, No. 7, pp. 2114–2129, Mar. 2014, https://doi.org/10.1016/j.jsv.2013.12.001

Publisher
M. Silveira, P. Wahi, and J. C. M. Fernandes, “Effects of asymmetrical damping on a 2 DOF quarter-car model under harmonic excitation,” Communications in Nonlinear Science and Numerical Simulation, Vol. 43, pp. 14–24, Feb. 2017, https://doi.org/10.1016/j.cnsns.2016.06.029

Publisher
D. D. Le and H. N. Tran, “An investigation of a bus’s ride comfort by using the quarter car model with linear asymmetric damper,” Journal of Vibroengineering, Vol. 25, No. 1, pp. 143–155, Feb. 2023, https://doi.org/10.21595/jve.2022.22811

Publisher
R. N. Jazar, Vehicle Dynamics Theory and Application. New York, USA: Springer, 2008.

Publisher
T. D. Gillespie, Fundamentals of Vehicle Dynamics Software. Warrendale, USA: SEA, 1992.

Publisher
J. C. Dixon, The Shock Absorber Handbook. USA: John Wiley and Sons, Ltd., 2007.

Publisher

Cited by

Analysis of a bus vertical dynamic performances – a comparison between linear and nonlinear suspension systems

Huu Nhan Tran | Ngoc Dai Pham

(2024)

About this article

Received

18 May 2023

Accepted

19 October 2023

Published

25 November 2023

SUBJECTS

Vibration in transportation engineering

DOI

https://doi.org/10.21595/jve.2023.23404

Keywords

bus suspension

vertical dynamic evaluation indexes

harmonic excitation

frequency domain

shock absorber characteristics

symmetric asymmetric

linear nonlinear

Acknowledgements

We acknowledge Ho Chi Minh City University of Technology (HCMUT), VNU-HCM for supporting this study.

Data Availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Author Contributions

Huu Nhan Tran: conceptualization, methodology, software, supervision, validation. Fergyanto E. Gunawan: visualization, writing – review and editing. Ngoc Dai Pham: data curation, formal analysis, resources, writing – original draft preparation

Conflict of interest

The authors declare that they have no conflict of interest.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2023 08 22

Mechanism of time-delay feedback control of suspension damping with an annular vibration-absorbing structure

Yajie Chen, Kehui Ma, Chuanbo Ren, Yang Nan, Pengcheng Zhou

Research article

2023 01 20

An investigation of a bus’s ride comfort by using the quarter car model with linear asymmetric damper

Dinh Duy Le, Huu Nhan Tran

Research article

2018 12 13

Study on the influence of bus suspension parameters on ride comfort

Le Xuan Long, Le Van Quynh, Bui Van Cuong

Research article

2018 06 30

Modeling and analysis of a high-static-low-dynamic stiffness vibration isolator with experimental investigation

Chun Cheng, Shunming Li, Yong Wang

H. N. Tran, F. E. Gunawan, and N. D. Pham, “Influence of a nonlinear asymmetric shock absorber on vibration of a bus subjected to harmonic excitation,” Journal of Vibroengineering, Vol. 26, No. 1, pp. 128–138, Nov. 2023, https://doi.org/10.21595/jve.2023.23404

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2023.23404
UR  - https://doi.org/10.21595/jve.2023.23404
TI  - Influence of a nonlinear asymmetric shock absorber on vibration of a bus subjected to harmonic excitation
T2  - Journal of Vibroengineering
AU  - Tran, Huu Nhan
AU  - E. Gunawan, Fergyanto
AU  - Pham, Ngoc Dai
PY  - 2023
DA  - 2023/11/25
PB  - Extrica
SP  - 128-138
VL  - 26
IS  - 1
SN  - 1392-8716
SN  - 2538-8460
ER  - 

Copy Ris

Copied to clipboard!

 @article{Tran_2023, title={Influence of a nonlinear asymmetric shock absorber on vibration of a bus subjected to harmonic excitation}, volume={26}, ISSN={2538-8460}, url={https://doi.org/10.21595/jve.2023.23404}, DOI={10.21595/jve.2023.23404}, number={1}, journal={Journal of Vibroengineering}, publisher={JVE International Ltd.}, author={Tran, Huu Nhan and E. Gunawan, Fergyanto and Pham, Ngoc Dai}, year={2023}, month=nov, pages={128–138} }

Copy Bibtex

Copied to clipboard!

[1]H. N. Tran, F. E. Gunawan, and N. D. Pham, “Influence of a nonlinear asymmetric shock absorber on vibration of a bus subjected to harmonic excitation,” Journal of Vibroengineering, vol. 26, no. 1, pp. 128–138, Nov. 2023, doi: 10.21595/jve.2023.23404.

Copy IEEE

Copied to clipboard!

Tran, Huu Nhan, Fergyanto E. Gunawan, and Ngoc Dai Pham. “Influence of a Nonlinear Asymmetric Shock Absorber on Vibration of a Bus Subjected to Harmonic Excitation.” Journal of Vibroengineering 26, no. 1 (November 25, 2023): 128–38. https://doi.org/10.21595/jve.2023.23404.

Copy Chicago

Copied to clipboard!

Influence of a nonlinear asymmetric shock absorber on vibration of a bus subjected to harmonic excitation

Abstract

Highlights

1. Introduction

2. Research method

2.1. Simulation model

2.2. Harmonic excitation

2.3. The four types of shock absorbers

2.4. Evaluation indexes

2.4.1. Gain response of SDD

2.4.2. Gain response of BVA

2.4.3. Tire dynamic load - TDL

2.4.4. Calculation flowchart

3. Results and discussions

3.1. Gain response of SDD

3.2. Gain response of SDDS

3.3. Gain response of BVA

3.4. Tire dynamic load – TDL

4. Conclusions

References

Cited by

About this article

Related Articles