Abstract
A monostable piezoelectric vibration energy harvester (VEH) model subject to Gaussian colored noise is studied in this paper. With the help of energy balance method, a concise expression of the transient frequency which is determined by transient amplitude is used in the stochastic averaging process. Then an Itô stochastic differential equation is obtained. The new expression of frequency can lead to pretty good probability density function (PDF) of the displacement, PDF of output electric voltage of the VEH model, even if the nonlinear stiffness coefficient is very large. The influence of the nonlinear stiffness coefficient on the PDFs and on the output electric voltage is detailed and discussed. It is found that the larger nonlinear stiffness coefficient is, the smaller motion range and smaller mean square value of electric voltage it will result in. Furthermore, the larger time delay coefficient of the colored noise is, the larger mean square value of electric voltage it will lead to. Numerical simulations verified the accuracy of this method.
Highlights
- Time delay coefficient of the colored noise has great influence on the mean square value of the voltage output.
- The lager nonlinear stiffness coefficient is, the smaller motion range and smaller mean square value of electric voltage it will result in.
- The improved stochastic averaging method can deal with piezoelectric vibrational energy harvester model excited by colored noise.
1. Introduction
In recent years, accumulating attention has been paid to the piezoelectric vibration energy harvesting (VEH) systems due to their capability of collecting the ambivalent background energy, which is usually free. Mathematical analysis on this topic is of great importance. One type of well-known vibration energy harvesting system, which is used to model a basally excited cantilever with piezoelectric ceramic layers attached to it, is displayed in the form:
The Eq. (1) and Eq. (2) describe the relation of motion states and piezoelectric voltage, where denotes the relative displacement of mass , denotes the basal acceleration, denotes the linear damping coefficient, denotes the potential energy of the conservative part of the mechanical subsystem, denotes the output voltage across the equivalent resistive load , is the piezoelectric capacitance, denotes electro-mechanical coupling coefficient, the dot represents the derivative with respect to time .
Introduce the non-dimensional parameters:
where denotes the linear stiffness coefficient of the conservative part , denotes a chosen character length, presents the dimensionless time, denotes the character time scale, denotes the dimensionless displacement, denotes the linear dimensionless damping coefficient, denotes the dimensionless basal acceleration. The Eq. (1) and Eq. (2) can be transformed to as follows:
where, the expression presents the combination of dimension less linear and nonlinear stiffness terms, i.e.. Based on this model, plenty of researches have been carried out. When (0), Eq. (3) is a duffing type (mono-stable) VEH [1-3], where is the dimensionless linear frequency, denotes the dimensionless nonlinear stiffness coefficient. When (0), Eq. (3) is called the bi-stable (double well) VEH [4]-[7]. When and has five real roots, Eq. (3) is called the tri-stable VEH [8]-[10]. When has much complex expressions, there even exists quadruple well VEH [11], [12] However, one should notice that the early researches were based on harmonic excitation, which could hardly simulate the noise in real-world. As the research deepens, a better method is in need for the research of VEH.
Daqaq [13], [14] applied the moment method based on the Fokker- Planck-Kolmogorov (FPK) equation to study a duffing type and a bi-stable VEH driven by white noise as well as colored noise. One striking conclusion was proposed: the mean square output voltage and the output power are proportional to the white noise density but have no relation with the nonlinear stiffness coefficient, i.e., the response of a white noise excited bi-stable VEH has no relation with the shape of the potential well. But Daqaq and He [15] found that the moment method could lead to large errors and even wrong predictions when the potential wells are deep enough. Similarly, Chen and Jiang [16] using the moment method, studied a VEH model with order-2 and order-4 nonlinear stiffness terms subject white noise. By then, one could find that the nonlinear stiffness term did have an influence on the responses. Subsequently, Chen and Jiang [17] applied an equivalent linearization technique to study a white noise excited VEH model with cubic nonlinearity. In their paper, the influence of the nonlinear stiffness was approximately simplified to be disturbing terms to the linear stiffness term and the linear damping term. Then, the two disturbing terms were obtained by the minimal mean square error principle.
Stochastic averaging method is another popular method in studying the randomly excited VEH for it can give the approximate probability density functions of different random variables. Chen and Jiang [18] applied the standard stochastic averaging method to solve some different types of VEH subject to white noise. In this paper, the displacement and velocity are assumed to be , (where denotes the transient amplitude and denotes the fundamental frequency). Although the influence of nonlinear stiffness on frequency is ignored, the method offers acceptable predications on condition that the nonlinearity is not strong. However, when the stiffness nonlinearity is strong, the standard stochastic averaging will lose its accuracy. Because, although nonlinear stiffness is taken into account during modeling, the stiffness nonlinear term will be eliminated in subsequent calculations. To solve this problem, Chen and Jiang [19] assumed the displacement and velocity in the form of , where the frequency is a so-called generalized harmonic functions, they obtained the averaged frequency by integrating the with respect to . Liu et al. [20], Li and Xu [21], Xu and Wang [22] applied the energy envelope stochastic averaging method and assumed the frequency is the function of the total mechanical energy H. The similarity of the references [19] and reference [20]-[22]is that they all concerned the nonlinear stiffness term had an influence on the response frequency, so they used an energy determined frequency and an amplitude determined frequency instead of the fundamental frequency . But both methods are very time-consuming, especially the second one. Because the explicit expression of the must be obtained by ellipse integrals, which cannot be easily expressed as polynomials or a fraction.
In recent years, significant progress has been made in relevant research. In 2018, Fang Fei et al. [23] investigated a VEH model subjected to parametric and external excitations. They considered stiffness nonlinearity using the Hamiltonian principle and studied the effects of damping, load coefficient, electromechanical coupling coefficient, and excitation amplitude on the frequency response curve. In 2019, Wang Yaobin et al. [24] investigated the electromechanical response of a VEH and observed that during the process of increasing stiffness nonlinearity, the softening behavior of the system first increases and then decreases. They discovered an optimal value for the stiffness nonlinearity. In 2020, Xia Guanghui et al. [25] utilized the multi-scale method to investigate the response of a VEH with an additional mass block under parametric excitation and direct excitation. They found that with an increase in the mass block, the system's stiffness nonlinearity coefficient decreases, leading to a softening behavior in the amplitude-frequency response curve. In 2020, Zhang Yanxia [26] investigated the stochastic bifurcation of a three-well piezoelectric cantilever beam under colored noise excitation, varying the third-order stiffness term, fifth-order stiffness term, noise intensity, and correlation time as bifurcation parameters. The study revealed that noise intensity can enhance the generation of average output power, while correlation time leads to a reduction in average power generation. In 2021, Costa [27] conducted a parameter study on the third-order nonlinear stiffness coefficient in a bistable VEH system subjected to harmonic excitation. The results showed that higher linear stiffness coefficient and lower nonlinear stiffness coefficient lead to better power output performance.
Based on the above, the traditional stochastic averaging methods eliminate the stiffness nonlinearity coefficient in the subsequent calculation process, which significantly affects the computational accuracy. Although some scholars attempt to compensate for this using t the energy envelope stochastic averaging method, the calculation results are challenging to obtain, and the computational process becomes cumbersome. Indeed, in recent years, an increasing number of scholars have been paying attention to the significance of stiffness nonlinearity. Various studies have demonstrated that stiffness nonlinearity indeed plays a crucial role in influencing the system's response. In this paper, a mono-stable VEH model subject to colored noise is investigated. An approximate frequency in polynomial form can be obtained by the energy balance method [28]. The will have a concise and explicit expression. Based on the obtained frequency , a stochastic averaging method for strong nonlinearity is carried out. After that, the stationary probability density function (PDF) of the displacement, the joint probability density function of the displacement and velocity, as well as the mean square voltage are all given theoretically and numerically. The key issue of this paper is to make sure the approximate frequency will maintain accurate prediction of the responses. Numerical simulations are carried out to verify the accuracy of this method.
2. The energy balance method
The mono-stable piezoelectric vibration energy harvester model (Duffing type) to be studied in this paper is as follows:
The stationary displacement, the velocity and the stationary voltage are assumed to be:
where , is the transient amplitude, is the random phase, denotes the transient frequency.
Substituting Eq. (7) into Eq. (6) yields:
Then substitute Eq. (7) and Eq. (8) into Eq. (5), one has:
Thus, the total mechanic energy (Hamilton function) of the Eq. (9) is as follows:
When 0° and 45°, the energy equals to the following, respectively:
Obviously, when the energy dissipated by the damping can balance the noise input energy, there must exists . One can solve out the to be determined frequency [28] as follows.
In view of that the dimensionless load coefficient is much smaller than 1, we have , it is reasonable to assum , then one has the approximate frequency:
Letting , finally one has:
In this section, an approximate frequency determined by amplitude is obtained. In the next section, this frequency will be used in the stochastic averaging procedure.
3. Stochastic averaging method
The stiffness term is defined as , the damping term is defined as . The nonlinear stiffness coefficient is assumed to be strong, while the damping term is weak, Eq. (5) can be rewritten as:
Taking derivative to with respect to time yields:
Eq. (17) can be simplified as:
Then, taking derivative to with respect to time , yields:
In which one has:
Combining the Eq. (17) and Eq. (18) and taking Eq. (19) and Eq. (20) into account, one has a pair of stochastic differential equations:
The above pair of equations can be rewritten to be the standard form as:
where:
The Eq. (23) and Eq. (24) can be simplified to the Itô stochastic differential equation:
where is the drift term while is the diffusion term, is the standard unit Brown's motion. The expression of and are given by the following formular:
where is the averaging operator, is the correlation function.
The noise density is 2, the time delay coefficient is , then has the form of:
where the operator presents the mathematical expectation, while is the Dirac-delta function.
The drift coefficient , and the diffusion coefficient are given as:
In which the coefficients are:
4. The stationary probability density functions
The averaged Fokker-Plank-Kolmogorov (FPK) equation associated with Itô Eq. (25) is of the form:
where is the transition probability density of displacement amplitude . Under assumption of the stationary solution of FPK equation for Eq. (30) is of the form:
where constant is the normalization constant.
Substituting Eq. (28), Eq. (29) into Eq. (31) yields the stationary PDF of the equivalent amplitude:
The stationary probability density of total mechanic energy i.e., Hamiltonian function can be obtained as follows:
The transient amplitude is solved as:
The joint stationary probability density of displacementand velocity can be further obtained from as follows:
where is the average time period defined as
By integrating Eq. (35), the PDF of the displacement as well as the PDF of the velocity is obtained as Eq. (36) and Eq. (37):
The approximate relation with the electric voltage and the mechanical states in Eq. (8) is simplified to be the Eq. (37) by replacing by :
Thus, the PDF of the electric voltage is obtained based on the Eq. (38):
The mean-square value of the electric voltage is also derived through the approximate relation Eq. (37):
5. Numerical simulations
The Monte Carlo method is applied to verify the effectiveness of the above theoretical predictions. The parameters in Eq. (5) and Eq. (6) are taken as: The parameters are set as: 1, 0.05, 0.01, 0.1, 0.05. The noise density is chosen as 0.001 and 0.002, and the time delay coefficient is chosen as 0.3, 0.5 and 0.8, separately. In order to emphasis the accuracy of this method, even if the nonlinear stiffness coefficient is significantly large, the coefficient is set as 20 and 50 during the simulation, respectively. The numerical solutions of the oscillator Eq. (2) could be obtained by an order-2stochastic Runge-Kutta algorithm [29]. The numerical solutions were obtained using MATLAB. For each combination, totally 2,000 sets of colored noise are imposed the Eq. (5) and Eq. (6). Each set of noise includes 60,000 numbers. The time step is set as . The last 10,000 steps are kept as the stationary responses. Finally, doing statistic on total stationary 2,000×10,000 values of and , the stationary probability density function (PDF) of the displacement and the voltage is represented by a dot plot. The theoretical solutions obtained using Eq. (36) and Eq. (39) in Mathematica are represented using solid lines. The figure of the standard stochastic averaging method is sourced from reference [17] and is presented using dashed lines.
Fig. 1The analytical solution and numerical solution of stationary PDFs of electric voltage and displacement: a), b) D= 0.002, λ= 0.5, α= 20 and 50; c), d) λ= 0.5, α= 50, D= 0.001 and D= 0.002; e), f) α= 50, D= 0.002, λ= 0.3 and 0.8. a), c) e) PDFs of displacement, b) d, f) PDFs of voltage. Solid lines: improved method in this paper, see Eq. (36) and Eq. (39); dashed lines: standard stochastic averaging method in reference [17]; dots: numerical simulation)
![The analytical solution and numerical solution of stationary PDFs of electric voltage and displacement: a), b) D= 0.002, λ= 0.5, α= 20 and 50; c), d) λ= 0.5, α= 50, D= 0.001 and D= 0.002; e), f) α= 50, D= 0.002, λ= 0.3 and 0.8. a), c) e) PDFs of displacement, b) d, f) PDFs of voltage. Solid lines: improved method in this paper, see Eq. (36) and Eq. (39); dashed lines: standard stochastic averaging method in reference [17]; dots: numerical simulation)](https://static-01.extrica.com/articles/23428/23428-img1.jpg)
a)
![The analytical solution and numerical solution of stationary PDFs of electric voltage and displacement: a), b) D= 0.002, λ= 0.5, α= 20 and 50; c), d) λ= 0.5, α= 50, D= 0.001 and D= 0.002; e), f) α= 50, D= 0.002, λ= 0.3 and 0.8. a), c) e) PDFs of displacement, b) d, f) PDFs of voltage. Solid lines: improved method in this paper, see Eq. (36) and Eq. (39); dashed lines: standard stochastic averaging method in reference [17]; dots: numerical simulation)](https://static-01.extrica.com/articles/23428/23428-img2.jpg)
b)
![The analytical solution and numerical solution of stationary PDFs of electric voltage and displacement: a), b) D= 0.002, λ= 0.5, α= 20 and 50; c), d) λ= 0.5, α= 50, D= 0.001 and D= 0.002; e), f) α= 50, D= 0.002, λ= 0.3 and 0.8. a), c) e) PDFs of displacement, b) d, f) PDFs of voltage. Solid lines: improved method in this paper, see Eq. (36) and Eq. (39); dashed lines: standard stochastic averaging method in reference [17]; dots: numerical simulation)](https://static-01.extrica.com/articles/23428/23428-img3.jpg)
c)
![The analytical solution and numerical solution of stationary PDFs of electric voltage and displacement: a), b) D= 0.002, λ= 0.5, α= 20 and 50; c), d) λ= 0.5, α= 50, D= 0.001 and D= 0.002; e), f) α= 50, D= 0.002, λ= 0.3 and 0.8. a), c) e) PDFs of displacement, b) d, f) PDFs of voltage. Solid lines: improved method in this paper, see Eq. (36) and Eq. (39); dashed lines: standard stochastic averaging method in reference [17]; dots: numerical simulation)](https://static-01.extrica.com/articles/23428/23428-img4.jpg)
d)
![The analytical solution and numerical solution of stationary PDFs of electric voltage and displacement: a), b) D= 0.002, λ= 0.5, α= 20 and 50; c), d) λ= 0.5, α= 50, D= 0.001 and D= 0.002; e), f) α= 50, D= 0.002, λ= 0.3 and 0.8. a), c) e) PDFs of displacement, b) d, f) PDFs of voltage. Solid lines: improved method in this paper, see Eq. (36) and Eq. (39); dashed lines: standard stochastic averaging method in reference [17]; dots: numerical simulation)](https://static-01.extrica.com/articles/23428/23428-img5.jpg)
e)
![The analytical solution and numerical solution of stationary PDFs of electric voltage and displacement: a), b) D= 0.002, λ= 0.5, α= 20 and 50; c), d) λ= 0.5, α= 50, D= 0.001 and D= 0.002; e), f) α= 50, D= 0.002, λ= 0.3 and 0.8. a), c) e) PDFs of displacement, b) d, f) PDFs of voltage. Solid lines: improved method in this paper, see Eq. (36) and Eq. (39); dashed lines: standard stochastic averaging method in reference [17]; dots: numerical simulation)](https://static-01.extrica.com/articles/23428/23428-img6.jpg)
f)
In Fig. 1, due to the fact that the standard stochastic averaging method will eliminate the nonlinear stiffness coefficient during the averaging process, one can see clearly that the standard stochastic averaging method exhibits significant errors when compared to the numerical solutions, and these errors increase as the stiffness nonlinearity becomes larger. However, the improved stochastic averaging method manages to maintain accurate predictions even when the stiffness nonlinearity is relatively large. Also, the larger the coefficient becomes, the higher peak values and smaller range of the PDF value it will result in. Furthermore, one should also notice that even if the frequency (see Eq. (14)) which is used in this method has very concise form, this form still offers very good accordance of the theoretical prediction and the numerical simulation. The Fig. 1. also indicates that the improved method offers good accuracy with the time delay coefficient ranging from 0.3 to 0.8. And the larger will lead to the larger range of motion.
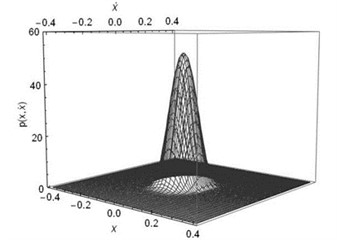
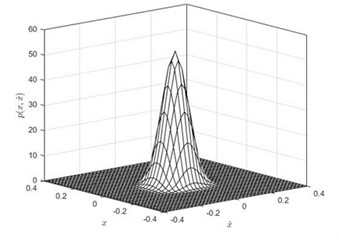
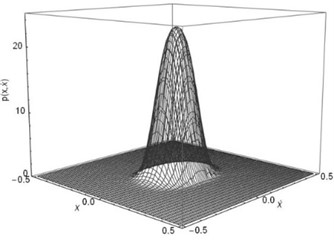
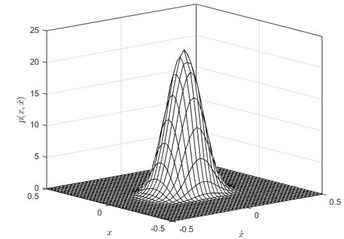
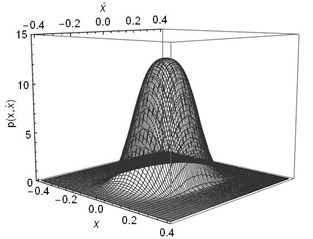
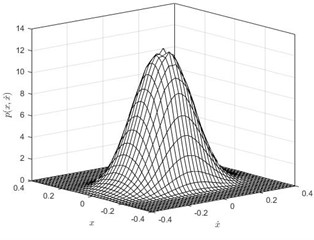
Fig. 2The joint Stationary PDF of displacement x and velocity y: a), b) for D= 0.002, λ= 0.3, λ= 50; c), d) for D= 0.002, λ= 0.5, α= 50; e), f) for D= 0.002, λ= 0.8, α= 50; a), c), e) are given by Eq. (35); b), d), f) are numerical simulation
a)
b)
c)
d)
e)
f)
Subsequently, the joint PDF of displacement and velocity are numerically simulated. In this part, the parameters are set as: 1, 0.05, 0.01, 0.1, , 0.002, 50. The time delay coefficient is chosen as 0.3, 0.5 and 0.8, separately. The numerical solutions were obtained using MATLAB. We take 40×40 grids in a range with a space gap:. Then we count the numbers (, 1-40) of the 2,000 ×60,000 stationary dots which fall within each grid. Finally, the joint PDF value of each grid can be calculated out by ). The theoretical solutions obtained using Eq. (32) and Eq. (35) in Mathematica. The joint PDFs are illustrated in Fig. 2. Fig. 2 shows that the theoretical predication on the joint probability density function of the displacement and velocity coincides with the numerical simulation.
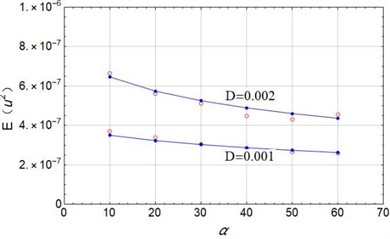
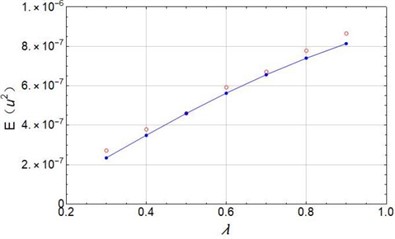
Finally, the mean square value of the electric voltage is predicted by the Eq. (40) and is numerically simulated. The Fig. 3(a) shows the results with the nonlinear stiffness coefficient ranging from 10 to 60. When noise density is chosen as 0.001 and 0.002, the Eq. (39) offers good accordance with the numerical simulation. Fig. 3(b) shows the good prediction with time delay coefficient ranging from 0.3 to 0.9. When is larger than 0.8, the error becomes visible. It is obvious that the larger nonlinear stiffness coefficient will lead to smaller mean square value of the electric voltage. While, larger time delay coefficient will result in larger .
Fig. 3Mean square voltage changes with system parameters: a) D= 0.001 and 0.002, λ= 0.5; b) D= 0.002, α= 50; Dotted lines: theoretical prediction by Eq. (40); circles: numerical simulation)
a)
b)
6. Conclusions
In this paper, an improved stochastic averaging method is introduced, the energy balance method has been employed to derive a concise expression of the transient frequency . The improved method significantly reduces computation time. Comparing with the standard stochastic averaging method, the improved method, considering the stiffness nonlinearity, demonstrates a notable improvement in predictive accuracy under colored noise excitation. The results are as follows:
1) This improved method has good accuracy in predicting the PDFs of the VEH system even if the expression of is short. This method can get rid of the disadvantage of large time consuming in calculating in references [19], [20]-[22].
2) The nonlinear coefficient does have an influence on the PDFs of displacement and electric voltage. Larger will result in smaller motion range, higher peak of PDFs and smaller mean square value of the voltage. Even if the is considerably large, this improved method maintains good accuracy.
3) Larger time delay coefficient will lead to larger motion range and larger mean square value of the voltage.
The improved stochastic averaging method introduced in this paper contributes to enhancing the output performance of piezoelectric transducers and deepens the understanding of the response patterns of single-steady-state models under random excitation.
References
-
A. Erturk and D. J. Inman, “An experimentally validated bimorph cantilever model for piezoelectric energy harvesting from base excitations,” Smart Materials and Structures, Vol. 18, No. 2, p. 025009, Feb. 2009, https://doi.org/10.1088/0964-1726/18/2/025009
-
M. Ferrari, V. Ferrari, M. Guizzetti, B. Andò, S. Baglio, and C. Trigona, “Improved energy harvesting from wideband vibrations by nonlinear piezoelectric converters,” Sensors and Actuators A: Physical, Vol. 162, No. 2, pp. 425–431, Aug. 2010, https://doi.org/10.1016/j.sna.2010.05.022
-
H. A. Sodano, G. Park, and D. J. Inman, “Estimation of electric charge output for piezoelectric energy harvesting,” Strain, Vol. 40, No. 2, pp. 49–58, May 2004, https://doi.org/10.1111/j.1475-1305.2004.00120.x
-
J.-T. Lin and B. Alphenaar, “Enhancement of energy harvested from a random vibration source by magnetic coupling of a piezoelectric cantilever,” Journal of Intelligent Material Systems and Structures, Vol. 21, No. 13, pp. 1337–1341, Sep. 2010, https://doi.org/10.1177/1045389x09355662
-
A. Erturk and D. J. Inman, “Broadband piezoelectric power generation on high-energy orbits of the bistable Duffing oscillator with electromechanical coupling,” Journal of Sound and Vibration, Vol. 330, No. 10, pp. 2339–2353, May 2011, https://doi.org/10.1016/j.jsv.2010.11.018
-
M. Ferrari, M. Baù, M. Guizzetti, and V. Ferrari, “A single-magnet nonlinear piezoelectric converter for enhanced energy harvesting from random vibrations,” Sensors and Actuators A: Physical, Vol. 172, No. 1, pp. 287–292, Dec. 2011, https://doi.org/10.1016/j.sna.2011.05.019
-
S. C. Stanton, C. C. Mcgehee, and B. P. Mann, “Nonlinear dynamics for broadband energy harvesting: Investigation of a bistable piezoelectric inertial generator,” Physica D: Nonlinear Phenomena, Vol. 239, No. 10, pp. 640–653, May 2010, https://doi.org/10.1016/j.physd.2010.01.019
-
J. Cao, S. Zhou, W. Wang, and J. Lin, “Influence of potential well depth on nonlinear tristable energy harvesting,” Applied Physics Letters, Vol. 106, No. 17, p. 17390, Apr. 2015, https://doi.org/10.1063/1.4919532
-
L. Haitao, Q. Weiyang, L. Chunbo, D. Wangzheng, and Z. Zhiyong, “Dynamics and coherence resonance of tri-stable energy harvesting system,” Smart Materials and Structures, Vol. 25, No. 1, p. 015001, Jan. 2016, https://doi.org/10.1088/0964-1726/25/1/015001
-
H.-X. Zou et al., “A broadband compressive-mode vibration energy harvester enhanced by magnetic force intervention approach,” Applied Physics Letters, Vol. 110, No. 16, p. 16390, Apr. 2017, https://doi.org/10.1063/1.4981256
-
C. Wang, Q. Zhang, and W. Wang, “Wideband quin-stable energy harvesting via combined nonlinearity,” AIP Advances, Vol. 7, No. 4, p. 04531, Apr. 2017, https://doi.org/10.1063/1.4982730
-
C. Wang, Q. Zhang, and W. Wang, “Low-frequency wideband vibration energy harvesting by using frequency up-conversion and quin-stable nonlinearity,” Journal of Sound and Vibration, Vol. 399, pp. 169–181, Jul. 2017, https://doi.org/10.1016/j.jsv.2017.02.048
-
M. F. Daqaq, “Response of uni-modal duffing-type harvesters to random forced excitations,” Journal of Sound and Vibration, Vol. 329, No. 18, pp. 3621–3631, Aug. 2010, https://doi.org/10.1016/j.jsv.2010.04.002
-
M. F. Daqaq, “Transduction of a bistable inductive generator driven by white and exponentially correlated Gaussian noise,” Journal of Sound and Vibration, Vol. 330, No. 11, pp. 2554–2564, May 2011, https://doi.org/10.1016/j.jsv.2010.12.005
-
Q. He and M. F. Daqaq, “New insights into utilizing bistability for energy harvesting under white noise,” Journal of Vibration and Acoustics, Vol. 137, No. 2, pp. 1–10, Apr. 2015, https://doi.org/10.1115/1.4029008
-
W.-A. Jiang and L.-Q. Chen, “Snap-through piezoelectric energy harvesting,” Journal of Sound and Vibration, Vol. 333, No. 18, pp. 4314–4325, Sep. 2014, https://doi.org/10.1016/j.jsv.2014.04.035
-
W.-A. Jiang and L.-Q. Chen, “An equivalent linearization technique for nonlinear piezoelectric energy harvesters under Gaussian white noise,” Communications in Nonlinear Science and Numerical Simulation, Vol. 19, No. 8, pp. 2897–2904, Aug. 2014, https://doi.org/10.1016/j.cnsns.2013.12.037
-
W.-A. Jiang and L.-Q. Chen, “Stochastic averaging of energy harvesting systems,” International Journal of Non-Linear Mechanics, Vol. 85, pp. 174–187, Oct. 2016, https://doi.org/10.1016/j.ijnonlinmec.2016.07.002
-
W.-A. Jiang and L.-Q. Chen, “Stochastic averaging based on generalized harmonic functions for energy harvesting systems,” Journal of Sound and Vibration, Vol. 377, pp. 264–283, Sep. 2016, https://doi.org/10.1016/j.jsv.2016.05.012
-
D. Liu, Y. Xu, and J. Li, “Probabilistic response analysis of nonlinear vibration energy harvesting system driven by Gaussian colored noise,” Chaos, Solitons and Fractals, Vol. 104, pp. 806–812, Nov. 2017, https://doi.org/10.1016/j.chaos.2017.09.027
-
M. Xu and X. Li, “Stochastic averaging for bistable vibration energy harvesting system,” International Journal of Mechanical Sciences, Vol. 141, pp. 206–212, Jun. 2018, https://doi.org/10.1016/j.ijmecsci.2018.04.014
-
M. Xu and Y. Wang, “Influence of restricted operating space on the performance of random vibration energy harvesting,” Journal of Vibration and Control, Vol. 26, No. 5-6, pp. 352–361, Mar. 2020, https://doi.org/10.1177/1077546319879539
-
F. Fang, G. Xia, and J. Wang, “Nonlinear dynamic analysis of cantilevered piezoelectric energy harvesters under simultaneous parametric and external excitations,” Acta Mechanica Sinica, Vol. 34, No. 3, pp. 561–577, Jun. 2018, https://doi.org/10.1007/s10409-017-0743-y
-
Y. Wang, “Study on the mechanical and electrical response of a piezoelectric cantilever beam,” Master’s Thesis, Nan Chang Hangkong University, 2019.
-
G. H. Xia and J. G. Wang, “Nonlinear dynamic analysis for a cantilever beam with a tip mass piezoelectric harvester under parametric and direct excitations with multi-scale method,” Journal of Vibration and Shock, Vol. 39, pp. 69–77, Sep. 2020, https://doi.org/10.13465/j.cnki.jvs.2020.19.011
-
Y. Zhang, Y. Jin, P. Xu, and S. Xiao, “Stochastic bifurcations in a nonlinear tri-stable energy harvester under colored noise,” Nonlinear Dynamics, Vol. 99, No. 2, pp. 879–897, Jan. 2020, https://doi.org/10.1007/s11071-018-4702-3
-
L. G. Costa, L. L. D. S. Monteiro, P. M. C. L. Pacheco, and M. A. Savi, “A parametric analysis of the nonlinear dynamics of bistable vibration-based piezoelectric energy harvesters,” Journal of Intelligent Material Systems and Structures, Vol. 32, No. 7, pp. 699–723, Apr. 2021, https://doi.org/10.1177/1045389x20963188
-
J.-H. He, “Preliminary report on the energy balance for nonlinear oscillations,” Mechanics Research Communications, Vol. 29, No. 2-3, pp. 107–111, Mar. 2002, https://doi.org/10.1016/s0093-6413(02)00237-9
-
R. L. Honeycutt, “Stochastic Runge-Kutta algorithms. II. Colored noise,” Physical Review A, Vol. 45, No. 2, pp. 604–610, Jan. 1992, https://doi.org/10.1103/physreva.45.604
About this article
The authors gratefully acknowledge the support of the Program for Innovative Research Team in University of Tianjin (No. TD 13-5037,60020301-52010107), the Natural Science Foundation of China (NSFC) through Grant Nos. 11402186, the Tianjin Research Program of Application Foundation and Advanced Technology through Grant No. 14JCQNJC05600, 18JCQNJC05300.
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
Yusen Li has contributions on modeling, simulation and writing. Gen Ge has contribution on theoretical analysis.
The authors declare that they have no conflict of interest.
