The optimization model of whole process engineering consulting consortium members based on Z-number

Liu, Zecheng; Chu, Jianyu; Du, Jinjian

doi:10.21595/jmai.2023.23600

Journal of Mechatronics and Artificial Intelligence in Engineering

Browse Journal

Submit article

Published: 30 October 2023

Check for updates

The optimization model of whole process engineering consulting consortium members based on Z-number

Zecheng Liu¹

Jianyu Chu²

Jinjian Du³

^{1, 2, 3}College of Civil and Architectural Engineering, North China University of Science and Technology, Tangshan, China

Corresponding Author:

Jianyu Chu

Cite the article Download PDF

Downloads 174

CrossRef Citations 1

Abstract

At present, there are very few enterprises with whole-process engineering consulting capability and qualification. To carry out consulting work in a consortium is a necessary way to meet the actual situation of the industry and promote whole-process consulting quickly, and the selection of consortium members is the key issue. First of all, this paper summarizes the construction principle of the index system of consortium member selection, and describes the index system. Aiming at the consortium member selection model, on the basis of comprehensive consideration of 9 indicators, the evaluation value of Z-Numbers fuzzy numbers is obtained by using seven-point language terms, the index weight and expert weight are obtained by using the sequential method and entropy weight method, and the data are processed to get the alternative enterprise evaluation matrix. Fuzzy TOPSIS method suitable for Z-Numbers was introduced to solve the positive ideal solution closeness degree of each enterprise, so as to rank the alternative enterprises.

Highlights

From three aspects of team cooperation, technical ability, organization and management, the whole process of project consulting consortium member selection evaluation index system including 9 indexes is put forward.
Z-numbers combined with entropy weight method were used to obtain the weight of expert opinions, and Z-Numbers fuzzy TOPSIS model was introduced to solve the ranking of alternative enterprises.
The uncertainty and reliability of decision information were fully considered. Fuzzy TOPSIS was used to calculate the distance between fuzzy numbers, reducing the loss of information.

1. Introduction

The interest distribution of relevant stakeholders is an important part of the whole process of engineering consultation in the form of a consortium. The interest distribution of all parties in the consortium is crucial to the smooth implementation of the project. Reasonable interest distribution can improve the enthusiasm of all parties for cooperation. Dissatisfaction of any party may lead to the dissolution of the consortium or the reduction of service quality [1].

Xu et al. [2] established a three-stage evaluation model for the selection of members in the design team, and conducted preliminary analysis, fuzzy comprehensive evaluation, and dynamic adjustment of candidate members. Through case studies, it has been verified that this method has strong flexibility and is suitable for various evaluation situations. Fan et al. [3] established a dual objective 0-1 model based on comprehensive consideration of personal information and collaboration ability for the screening problem of R&D team members, and applied it to an example to solve it using genetic algorithm, verifying the feasibility of the model. Watanabe et al. [4] introduced visual analysis methods into the study of member selection. Based on the collected information, they systematically analyzed the basic indicators of candidate members and visualized the evaluation process and prediction results of candidate members. Kumar et al. [5] used the fuzzy analytic hierarchy process to calculate indicator weights, combined with the decision-making method of fuzzy multi-objective optimization, established an optimization model, and obtained the ranking of candidate members. Cheng et al. [6] established a partner selection model in the supplier selection problem, with the constraints of cost, quality, completion time, and service quality in lean systems, and the goal of reducing time consumption.

In summary, research on the selection of consortium members in supply chain, transportation, virtual enterprises, and other fields is extensive and in-depth. However, the acquisition of decision-making information lacks judgment on the reliability of information, and there is a possibility of information loss during the evaluation process. China's whole Process engineering consulting is still in its infancy. For small and medium-sized consulting enterprises to form a consortium, the lead enterprise should also establish a member selection model based on the internal characteristics and development status of the whole Process engineering consulting

2. The whole process of project consulting consortium member selection index system

The selection index of engineering consulting members in the whole process is screened and the index system is established. Member Member selection indicators are shown in Table 1. The meanings of specific indicators are as follows.

Table 1Member selection evaluation index

Target	First-order index	Secondary index
Whole process project consulting consortium member selection evaluation index	Collaboration ability	Collaborative experience
		Ability to communicate
		Team-work ability
	Technical capacity	Enterprise qualification
		Quality of personal
		Relevant project experience
	Ability to organize and manage	Organization chart
		Incentive mechanism
		Enterprise culture

2.1. Index weight determination

The sequential method is a subjective weighting method. In the process of implementation, there is no need to construct judgment matrix and consistency test, and expert opinions can be fully expressed. There is no restriction on the number of indicators, and it has a good effect in determining the weight of indicators. The method firstly sorted the whole index, then compared the importance of adjacent indexes from weak to strong in pairs, and finally determined the weight of indexes by quantitative calculation by substituting the formula.

1) Deterministic order relation.

Suppose there are $n$ indicators in the index system. Respectively expressed as $x_{1}$ , $x_{2}$ … $x_{3}$ . Its weight is expressed as $w_{1}$ , $w_{2}$ … $w_{3}$ . The importance of indicators is ranked by experts, and after ranking, it is represented by $x_{1}^{*} > x_{2}^{*} \dots x_{n}^{*}$ . The weight is expressed as $w_{1}^{*}, w_{2}^{*} \dots w_{n}^{*}$ ．

2) Comparison of the importance of adjacent indicators.

Expert on adjacent indicators $x_{j - 1}^{*}$ and $x_{j}^{*}$ Compared to the importance of the evaluation, Getting the importance assignment $r_{j}$ , $r_{j} = w_{j - 1} / w_{j} (j = 2,3 \dots, n)$ , at the same time must satisfy $r_{j - 1} > 1 / r_{j}$ , degree of importance. The assignments $r_{j}$ are shown in Table 2.

Table 2Importance assignment

$r_{j}$	Assignment specification
1.0	Indicator $x_{j - 1}^{}$ is as important as indicator $x_{j}^{}$
1.2	Indicator $x_{j - 1}^{*}$ is slightly more important than indicator
1.4	Indicator $x_{j - 1}^{}$ is significantly more important than indicator $x_{j}^{}$
1.6	Indicator $x_{j - 1}^{}$ is more important than indicator $x_{j}^{}$
1.8	Indicator $x_{j - 1}^{}$ is extremely important than indicator $x_{j}^{}$

3) Calculated weight.

According to Eq. (1), the weight of the least important index is obtained, and according to formula (2), the weight of other indicators is obtained successively [6]:

1

w_{n}^{*} = \frac{1}{1 + \sum_{i = 2}^{n} \overset{n}{\prod_{i = k}}}, (j = n, n - 1, \dots 2),

2

w_{j - 1}^{*} = r_{j} w_{j}^{*}, (j = n, n - 1, \dots 2) .

3. Whole process engineering consulting consortium member selection model

3.1. Modeling idea

The leading unit of the consortium selects the best partners for the whole process engineering consulting project, which is not only conducive to the smooth development of the project, but also conducive to the smooth implementation of the whole process engineering consulting model in the form of a joint body. Therefore, in view of the principle of selecting the best members, several experts were invited to evaluate and score the indicators of the alternative members based on Z-numbers method. The weight of each indicator was calculated by the sequential method. The weight of each expert was obtained by using the information reliability part of Z-numbers combined with the entropy weight method, and the data were summarized and substituted into fuzzy TOPSIS method. The positive and negative ideal distance of each member is calculated, and the member is ranked to determine the consortium cooperative enterprises

Fig. 1Member selection flowchart

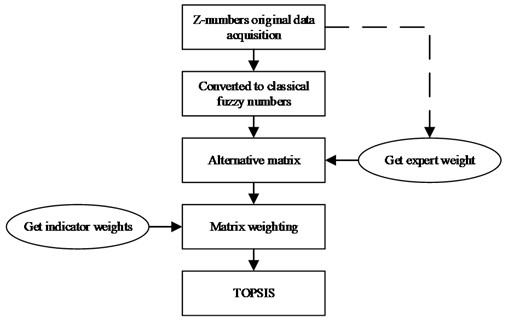
3.2. Z-numbers obtaining and processing data

3.2.1. The transformation of language variables

Language terms have fuzziness and uncertainty, which conform to the fuzzy limitation and reliability principle of Z-numbers. Studies show that language variables have the best effect between 6-10 partitions. If the score interval of language terms is too small, experts will not consider the relevant information of the evaluation object comprehensively, which will affect the accuracy of data. If the score interval of language terms is too large, experts should have high evaluation experience, evaluation efficiency, knowledge reserve and other conditions, and the amount of evaluation tasks of experts should be increased. Therefore, the 7-point conversion rule of language variables is adopted in this paper to convert the first part and the second part of Z-numbers into trapezoidal fuzzy numbers and triangular fuzzy numbers respectively. The conversion rules of language variables are shown in Table 3 and Table 4.

Table 3Constraint language variables and trapezoidal fuzzy number conversion rules

Serial number	Constrains some language variables	Corresponding fuzzy number
1	VP	(0,0,0.1,0.2)
2	P	(0.1,0.2,0.2,0.3)
3	MP	(0.2,0.3,0.4,0.5)
4	M	(0.4,0.5,0.5,0.6)
5	MG	(0.5,0.6,0.7,0.8)
6	G	(0.7,0.8,0.8,0.9)
7	VG	(0.8,0.9,1,1)

Table 4Conversion rules of reliability language variables and triangular fuzzy numbers

Serial number	Constrains some language variables	Corresponding fuzzy number
1	VL	(0,0,0.2)
2	L	(0.05,0.2,0.35)
3	ML	(0.2,0.35,0.5)
4	M	(0.35,0.5,0.65)
5	MH	(0.5,0.65,0.8)
6	H	(0.65,0.8,0.95)
7	VH	(0.8,1,1)

3.2.2. Z-Numbers are converted to classical fuzzy numbers

Kang proposed a method that can approximate Z-Numbers into classical fuzzy numbers under the premise of partial loss of information, which is conducive to improving decision efficiency and practical application. Its basic thinking path is as follows: First, let $Z = (A, B)$ be a Z-Number, Where A is the restrictive part, and the membership function is 1 $\{A = (x, μ_{A}) |x \in [0,1]\}$ , $B$ is the reliability part. The membership function is expressed as $\{B = (x, μ_{B}) |x \in [0,1]\}$ ; Part $B$ of reliability judgment is transformed according to gravity center method. You get a clear number $λ$ for a fuzzy number $B$ , As shown in Eq. (3). For triangular fuzzy numbers the results of centroid calculation formula are shown in Eq. (4):

3

λ = \frac{\int x B (x) d x}{\int B (x) d x},

4

λ = \frac{b_{1} + b_{2} + b_{3}}{3} .

Then, the barycenter value $λ$ of reliability part $B$ can be used as the weight of restriction part $A$ . Then $Z = (A, B)$ can be converted into the classical trapezoidal fuzzy number $Z^{'}$ . As shown in Eq. (5). If the constraint part $A$ is a trapezoidal fuzzy number, it can be expressed as Eq. (6):

5

Z^{'} = \{(x, μ_{^{^{A^{'}}}}) |μ_{^{^{A^{'}}}} (x) = λ μ_{A} (x), x \in [0,1]\},

6

Z^{'} = \sqrt{λ} \times A = (\sqrt{λ} \times a_{1}, \sqrt{λ} \times a_{2}, \sqrt{λ} \times a_{3}, \sqrt{λ} \times a_{4}) .

3.3. Expert weight calculation

The initial evaluation data contains the opinions of several experts, which need to be integrated to calculate the weight of each expert opinion. The reliability part of Z-Numbers represents the degree of experts' understanding of the information of evaluation objects. It can be used to calculate the weight of experts by combining the entropy weight method with the reliability part. When an expert has a full understanding of the information of evaluation objects, the accuracy of his evaluation will be higher, so the weight of the expert will be higher. The expert weight is calculated as shown in Eqs. (7), (8) and (9):

7

Z_{i j}^{x} = \frac{a + 4 b + c}{6},

8

\partial_{x}^{Z} = - \frac{1}{\sum_{i = 1}^{m} \sum_{j = 1}^{n} Z_{i j}^{x}} l n (\sum_{i = 1}^{m} \sum_{j = 1}^{n} Z_{i j}^{x}),

9

β_{x} = \frac{\partial_{x}^{Z}}{\sum_{x = 1}^{k} \partial_{x}^{Z}},

where $β_{x}$ represents the weight of the $x$ TH expert, $\partial_{x}^{Z}$ represents the reliability function of the $x$ TH expert opinion, $Z_{i j}^{x}$ represents the reliability value of the evaluation opinion of the $x$ TH expert on the $j$ TH index of the $i$ TH evaluation object. That is, the reliability of Z-Numbers is partially clarified. There are a total of $k$ experts, $m$ evaluation objects and $n$ evaluation indicators. Eqs. (10) and (11) were used to integrate the opinions of several evaluation experts into the evaluation matrix of alternative members:

10

β Z = （β a_{1}, β a_{2}, β a_{3}, β a_{4}）,

11

H_{i j} = β_{1} Z_{i j}^{1} + β_{2} Z_{i j}^{2} + \dots + β_{k} Z_{i j}^{k} .

3.4. TOPSIS determines the member ordering

1) The index weight obtained by the sequential method is weighted to the evaluation matrix of alternative members, as shown in Eq. (12), where $α_{j}$ represents the weight of the $j$ th index:

12

P = (α_{j} H_{i j})_{m \times n}^{} .

2) Determine the most ideal index $A^{+}$ and the least ideal index $A^{-}$ :

13

A^{+} = (P_{1}^{+}, P_{2}^{+} \dots P_{n}^{+}),

14

A^{-} = (P_{1}^{-}, P_{2}^{-} \dots P_{n}^{-}),

When the $j$ indicator is a benefit indicator, it is shown in Eq. (15). When the $j$ indicator is a cost-type indicator, it is shown in Eq. (16):

15

P_{j}^{+} = (\underset{i}{m a x} p_{i j}, j \in J_{1}; \underset{i}{m i n} p_{i j}, j \in J_{2}),

16

P_{j}^{-} = (\underset{i}{m i n} p_{i j}, j \in J_{1}; \underset{i}{m a x} p_{i j}, j \in J_{2}) .

3) Solve the positive and negative ideal distance. The distance calculation of two trapezoidal fuzzy numbers is shown in Eqs. (17) and (18), and the distance calculation of two trapezoidal fuzzy numbers is shown in Eq. (19):

17

d_{i}^{+} = \sum_{j = 1}^{n} d (p_{i j}, p_{j}^{+}),

18

d_{i}^{-} = \sum_{j = 1}^{n} d (p_{i j}, p_{j}^{-}),

19

d (a, b) = \sqrt{\frac{1}{6} [\sum_{i = 1}^{4} (b_{i} - a_{i})^{2} + \sum_{i = 1}^{3} (b_{i} - a_{i}) (b_{i + 1} - a_{i + 1})]} .

4) Solve the ideal point distance. Where, $θ_{i}$ represents the degree of closeness between the $i$ TH evaluation object and the positive ideal solution:

20

θ_{i} = d_{i}^{-} / (d_{i}^{+} + d_{i}^{-}) .

5) When sorting alternative units, the larger the $θ_{i}$ value is, the better the evaluation object is and the more it meets the selection demand of the lead unit. The largest $θ_{i}$ value belongs to the consortium partner.

4. Example

Currently, a design institute, as the lead enterprise, has formed a consortium to carry out the whole process of CBD construction engineering consulting project of a city business district. The design institute can provide design services and construction cost services. The project owner requires the whole process of engineering consulting services including supervision services. All submitted relevant information about their enterprises.

4.1. Determine index weight

The weight of each index is determined by the sequential method, as shown in Table 5.

Table 5Weight of each indicator

First-order index	First-order index weight	Secondary index	Secondary index weight	Comprehensive weight
Collaboration ability	0.31	Collaborative experience	0.396	0.123
		Ability to communicate	0.275	0.085
		Team-work ability	0.33	0.102
Technical capacity	0.434	Enterprise qualification	0.245	0.106
		Quality of personal	0.412	0.179
		Relevant project experience	0.343	0.149
Ability to organize and manage	0.258	Organization chart	0.467	0.120
		Incentive mechanism	0.292	0.075
		Enterprise culture	0.243	0.063

4.2. Evaluation and scoring

4 industry experts are invited to evaluate A, B and C enterprises according to the 7-point scale terms, as shown in Table 6, 7 and 8.

4.3. Z-numbers transform

Z-Numbers are converted into classical fuzzy numbers, as shown in Table 9, Table 10 and Table 11.

4.4. Calculated expert weight

The reliability part of Z-numbers is clarified according to Eq. (7), the expert weight is calculated according to Eqs. (8) and (9), and the member selection evaluation matrix is obtained according to the index weight, as shown in Table 12.

4.5. TOPSIS calculates the rankings

Since indexes in this paper are benefit indexes, the values of positive and negative ideal solutions are treated as $J_{1}$ . The positive and negative ideal distance of each unit in TOPSIS is shown in Table 13. The value of the alternative units is $θ_{1} =$ 0.850, $θ_{2} =$ 0.154, $θ_{3} =$ 0.625. Among them, Unit A has the highest evaluation value, that is, Unit A is the optimal partner.

The calculation results show that, after the evaluation of the indicators of the three supervision units A, B and C by four experts, the model-based calculation and analysis results show that unit A is the best and has obvious advantages. In reality, Unit A has advantages in technical ability and team cooperation ability, which is in line with the realistic results and verifies the applicability of the model.

Table 6A Unit expert evaluation language value

		Expert 1	Expert 2	Expert 3	Expert 4
U₁	U₁₁	(MG,H)	(G,H)	(G,MH)	(MG,MH)
	U₁₂	(MG,MH)	(M,H)	(MG,M)	(MG,MH)
	U₁₃	(MG,VH)	(M,M)	(MG,M)	(MG,H)
U₂	U₂₁	(MG,ML)	(G,H)	(MG,H)	(VG,ML)
	U₂₂	(M,MH)	(MG,ML)	(MG,H)	(VG,H)
	U₂₃	(MG,M)	(G,MH)	(G,ML)	(M,M)
U₃	U₃₁	(MG,M)	(M,M)	(MG,MH)	(M,MH)
	U₃₂	(M,VH)	(MP,MH)	(MG,H)	(MP,MH)
	U₃₃	(MG,M)	(MP,H)	(MP,M)	(M,M)

Table 7B Unit expert evaluation language value

		Expert 1	Expert 2	Expert 3	Expert 4
U₁	U₁₁	(M, H)	(M, M)	(P,MH)	(MP,MH)
	U₁₂	(P,MH)	(MP,MH)	(M,M)	(M,H)
	U₁₃	(M,H)	(M, MH)	(MP,ML)	(P,MH)
U₂	U₂₁	(MG,H)	(M, MH)	(MG,H)	(M,H)
	U₂₂	(MP,MH)	(M,ML)	(MP,H)	(M,M)
	U₂₃	(M,M)	(P,MH)	(MP,MH)	(P,MH)
U₃	U₃₁	(MG,H)	(M,MH)	(MG,H)	(MG,M)
	U₃₂	(MP,M)	(M,M)	(G,ML)	(M,ML)
	U₃₃	(G,H)	(MG,H)	(M,MH)	(MG,H)

Table 8C Unit expert evaluation language value

		Expert 1	Expert 2	Expert 3	Expert 4
U₁	U₁₁	(MG,MH)	(MG,M)	(M,H)	(M,MH)
	U₁₂	(M,M)	(MG,VH)	(MG,M)	(MG,ML)
	U₁₃	(M,MH)	(MG,ML)	(MP,M)	(G,M)
U₂	U₂₁	(M,MH)	(MG,M)	(G,ML)	(MG,M)
	U₂₂	(MG,M)	(M,M)	(G,MH)	(M,MH)
	U₂₃	(M,H)	(MG,MH)	(M,ML)	（MG,MH）
U₃	U₃₁	(MG,MH)	(M,M)	(MG,H)	(MG,VH)
	U₃₂	(M,ML)	(MP,M)	(G,H)	(MG,MH)
	U₃₃	(M,M)	(MG,MH)	(MG,M)	(M,M)

Table 9A unit classical fuzzy number

	Expert 1	Expert 2	Expert 3	Expert 4
U₁₁	0.447,0.537,0.626,0.716	0.626,0.716,0.716,0.805	0.564,0.645,0.645,0.726	0.403,0.484,0.564,0.645
U₁₂	0.403,0.484,0.564,0.645	0.358,0.447,0.447,0.537	0.354,0.424,0.495,0.566	0.403,0.484,0.564,0.645
U₁₃	0.483,0.58,0.676,0.773	0.283,0.354,0.354,0.424	0.354,0.424,0.495,0.566	0.447,0.537,0.626,0.716
U₂₁	0.296,0.355,0.414,0.473	0.626,0.716,0.716,0.805	0.447,0.537,0.626,0.716	0.473,0.532,0.592,0.592
U₂₂	0.322,0.403,0.403,0.484	0.296,0.355,0.414,0.473	0.447,0.537,0.626,0.716	0.716,0.805,0.894,0.894
U₂₃	0.354,0.424,0.495,0.566	0.564,0.645,0.645,0.726	0.414,0.473,0.473,0.532	0.283,0.354,0.354,0.424
U₃₁	0.354,0.424,0.495,0.566	0.283,0.354,0.354,0.424	0.414,0.473,0.473,0.532	0.322,0.403,0.403,0.484
U₃₂	0.386,0.483,0.483,0.58	0.161,0.242,0.322,0.403	0.447,0.537,0.626,0.716	0.161,0.242,0.322,0.403
U₃₃	0.354,0.424,0.495,0.566	0.179,0.268,0.358,0.447	0.141,0.212,0.283,0.354	0.283,0.354,0.354,0.424

Table 10B unit classical fuzzy number

	Expert 1	Expert 2	Expert 3	Expert 4
U₁₁	0.358,0.447,0.447,0.537	0.283,0.354,0.354,0.424	0.081,0.161,0.161,0.242	0.161,0.242,0.322,0.403
U₁₂	0.081,0.161,0.161,0.242	0.161,0.242,0.322,0.403	0.283,0.354,0.354,0.424	0.358,0.447,0.447,0.537
U₁₃	0.358,0.447,0.447,0.537	0.322,0.403,0.403,0.484	0.118,0.177,0.237,0.296	0.081,0.161,0.161,0.242
U₂₁	0.447,0.537,0.626,0.716	0.322,0.403,0.403,0.484	0.447,0.537,0.626,0.716	0.358,0.447,0.447,0.537
U₂₂	0.161,0.242,0.322,0.403	0.237,0.296,0.296,0.355	0.179,0.268,0.358,0.447	0.283,0.354,0.354,0.424
U₂₃	0.283,0.354,0.354,0.424	0.081,0.161,0.161,0.242	0.161,0.242,0.322,0.403	0.081,0.161,0.161,0.242
U₃₁	0.447,0.537,0.626,0.716	0.322,0.403,0.403,0.484	0.447,0.537,0.626,0.716	0.354,0.424,0.495,0.566
U₃₂	0.141,0.212,0.283,0.354	0.283,0.354,0.354,0.424	0.414,0.473,0.473,0.532	0.237,0.296,0.296,0.355
U₃₃	0.626,0.716,0.716,0.805	0.447,0.537,0.626,0.716	0.322,0.403,0.403,0.484	0.447,0.537,0.626,0.716

Table 11C unit classical fuzzy number

	Expert 1	Expert 2	Expert 3	Expert 4
U₁₁	0.403,0.484,0.564,0.645	0.354,0.424,0.495,0.566	0.358,0.447,0.447,0.537	0.322,0.403,0.403,0.484
U₁₂	0.283,0.354,0.354,0.424	0.483,0.58,0.676,0.773	0.354,0.424,0.495,0.566	0.296,0.355,0.414,0.473
U₁₃	0.322,0.403,0.403,0.484	0.296,0.355,0.414,0.473	0.141,0.212,0.283,0.354	0.495,0.566,0.566,0.636
U₂₁	0.322,0.403,0.403,0.484	0.354,0.424,0.495,0.566	0.414,0.473,0.473,0.532	0.354,0.424,0.495,0.566
U₂₂	0.354,0.424,0.495,0.566	0.283,0.354,0.354,0.424	0.564,0.645,0.645,0.726	0.322,0.403,0.403,0.484
U₂₃	0.358,0.447,0.447,0.537	0.403,0.484,0.564,0.645	0.237,0.296,0.296,0.355	0.403,0.484,0.564,0.645
U₃₁	0.403,0.484,0.564,0.645	0.283,0.354,0.354,0.424	0.447,0.537,0.626,0.716	0.483,0.58,0.676,0.773
U₃₂	0.237,0.296,0.296,0.355	0.141,0.212,0.283,0.354	0.626,0.716,0.716,0.805	0.403,0.484,0.564,0.645
U₃₃	0.283,0.354,0.354,0.424	0.403,0.484,0.564,0.645	0.354,0.424,0.495,0.566	0.283,0.354,0.354,0.424

Table 12Alternative enterprise member selection evaluation matrix

	Company A	Company B	company C
U₁₁	0.0628, 0.0734, 0.0785, 0.0890	0.0270, 0.0369, 0.0393, 0.0492	0.0442, 0.0540, 0.0586, 0.0686
U₁₂	0.0322, 0.0391, 0.0439, 0.0508	0.0188, 0.0257, 0.0274, 0.0342	0.0302, 0.0365, 0.0413, 0.0476
U₁₃	0.0399, 0.0482, 0.0547, 0.0630	0.0223, 0.0302, 0.0317, 0.0397	0.0319, 0.0391, 0.0424, 0.0496
U₂₁	0.0490, 0.0569, 0.0624, 0.0687	0.0417, 0.0509, 0.0556, 0.0649	0.0383, 0.0457, 0.0495, 0.0570
U₂₂	0.0798, 0.0940, 0.1047, 0.1150	0.0385, 0.0520, 0.0595, 0.0729	0.0682, 0.0818, 0.0849, 0.0985
U₂₃	0.0603, 0.0707, 0.0733, 0.0838	0.0224, 0.0341, 0.0371, 0.0487	0.0522, 0.0637, 0.0697, 0.0812
U₃₁	0.0412, 0.0496, 0.0517, 0.0601	0.0471, 0.0570, 0.0644, 0.0744	0.0485, 0.0586, 0.0665, 0.0767
U₃₂	0.0216, 0.0282, 0.0329, 0.0394	0.0202, 0.0251, 0.0264, 0.0313	0.0264, 0.0321, 0.0349, 0.0406
U₃₃	0.0150, 0.0197, 0.0234, 0.0281	0.0289, 0.0344, 0.0373, 0.0428	0.0209, 0.0255, 0.0279, 0.0325

Table 13Positive and negative ideal distances in fuzzy topsis

		Company A		Company B		Company C
		$d (p_{1 j}, p_{j}^{+})$	$d (p_{1 j}, p_{j}^{-})$	$d (p_{2 j}, p_{j}^{+})$	$d (p_{2 j}, p_{j}^{-})$	$d (p_{3 j}, p_{j}^{+})$	$d (p_{3 j}, p_{j}^{-})$
T₁	T₁₁	0.0000	0.0409	0.0409	0.0000	0.0212	0.0197
	T₁₂	0.0000	0.0163	0.0163	0.0000	0.0028	0.0134
	T₁₃	0.0000	0.0223	0.0223	0.0000	0.0117	0.0106
T₂	T₂₁	0.0000	0.0126	0.0066	0.0063	0.0126	0.0000
	T₂₂	0.0000	0.0463	0.0463	0.0000	0.0166	0.0299
	T₂₃	0.0000	0.0394	0.0394	0.0000	0.0062	0.0337
T₃	T₃₁	0.0134	0.0000	0.0021	0.0114	0.0000	0.0134
	T₃₂	0.0035	0.0057	0.0085	0.0000	0.0000	0.0085
	T₃₃	0.0154	0.0000	0.0000	0.0154	0.0099	0.0056

5. Conclusions

To carry out consulting work in a consortium is a necessary way to effectively promote the whole process of engineering consulting. From three aspects of team cooperation, technical ability, organization and management, the whole process of project consulting consortium member selection evaluation index system including 9 indexes is put forward. Z-numbers combined with entropy weight method were used to obtain the weight of expert opinions, and Z-Numbers fuzzy TOPSIS model was introduced to solve the ranking of alternative enterprises. The uncertainty and reliability of decision information were fully considered. Fuzzy TOPSIS was used to calculate the distance between fuzzy numbers, reducing the loss of information. It can reflect the reality well. The applicability of the model is verified by an example. The optimization model of the consortium members in the whole process of engineering consulting provides a feasible method to solve the problem of leading enterprises choosing partners.

References

S. M. Cui, “Research on the income distribution model of the whole process engineer consulting consortium,” (in Chinese), Construction Economy, Vol. 42, No. 3, pp. 37–40, 2021.

Search CrossRef
Y. T. Xu, Y. Wang, and X. D. Gao, “Collaborative design team formation method based on three-phase comprehensive evaluation,” (in Chinese), in International Conference on Information Science and Engineering, Vol. 35, No. 7, pp. 1907–1910, 2010.

Search CrossRef
Z. P. Fan, B. Feng, and Z. Z. Jiang, “A method for member selection of R&D teams using the individual and collaborative information,” (in Chinese), Expert Systems with Applications, Vol. 36, No. 4, pp. 8313–8323, 2009.

Publisher
R. Watanabe, H. Ishibashi, and T. Furukawa, “Visual analytics of set data for knowledge discovery and member selection support,” Decision Support Systems, Vol. 152, No. 1, p. 113635, Jan. 2022, https://doi.org/10.1016/j.dss.2021.113635

Publisher
D. Kumar, Z. Rahman, and F. T. S. Chan, “A fuzzy AHP and fuzzy multi-objective linear programming model for order allocation in a sustainable supply chain,” International Journal of Computer Integrated Manufacturing, Vol. 30, No. 6, pp. 535–551, Jun. 2017, https://doi.org/10.1080/0951192x.2016.1145813

Publisher
Y. Cheng, J. Peng, Z. Zhou, X. Gu, and W. Liu, “A Hybrid DEA-Adaboost model in supplier selection for fuzzy variable and multiple objectives,” (in Chinese), IFAC-PapersOnLine, Vol. 50, No. 1, pp. 12255–12260, Jul. 2017, https://doi.org/10.1016/j.ifacol.2017.08.2038

Publisher
M. M. Zhao, “Research on EPC engineering consortium based on Z-number fuzzy numbers,” (in Chinese), China Three Gorges University, Yichang, 2019.

Search CrossRef

Cited by

2024 International Conference on Big Data and Digital Management

Hongji Fang

(2024)

About this article

Received

31 August 2023

Accepted

11 October 2023

Published

30 October 2023

DOI

https://doi.org/10.21595/jmai.2023.23600

Keywords

whole-process consultation

member selection

Z-numbers

TOPSIS

Acknowledgements

This research is supported by National Science and Technology support program (2013BAJ10B09-2).

Data Availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Author Contributions

Zecheng Liu: data curation, formal analysis, investigation, methodology, visualization, writing-original draft preparation. Jianyu Chu: conceptualization, funding acquisition, supervision, validation. Jinjian Du: project administration, software, writing-review and editing.

Conflict of interest

The authors declare that they have no conflict of interest.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Z. Liu, J. Chu, and J. Du, “The optimization model of whole process engineering consulting consortium members based on Z-number,” Journal of Mechatronics and Artificial Intelligence in Engineering, Vol. 4, No. 2, pp. 112–121, Oct. 2023, https://doi.org/10.21595/jmai.2023.23600

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jmai.2023.23600
UR  - https://doi.org/10.21595/jmai.2023.23600
TI  - The optimization model of whole process engineering consulting consortium members based on Z-number
T2  - Journal of Mechatronics and Artificial Intelligence in Engineering
AU  - Liu, Zecheng
AU  - Chu, Jianyu
AU  - Du, Jinjian
PY  - 2023
DA  - 2023/10/30
PB  - JVE International Ltd.
SP  - 112-121
VL  - 4
IS  - 2
SN  - 2669-1116
ER  - 

Copy Ris

Copied to clipboard!

 @article{Liu_2023, title={The optimization model of whole process engineering consulting consortium members based on Z-number}, volume={4}, ISSN={2669-1116}, url={https://doi.org/10.21595/jmai.2023.23600}, DOI={10.21595/jmai.2023.23600}, number={2}, journal={Journal of Mechatronics and Artificial Intelligence in Engineering}, publisher={JVE International Ltd.}, author={Liu, Zecheng and Chu, Jianyu and Du, Jinjian}, year={2023}, month=oct, pages={112–121} }

Copy Bibtex

Copied to clipboard!

[1]Z. Liu, J. Chu, and J. Du, “The optimization model of whole process engineering consulting consortium members based on Z-number,” Journal of Mechatronics and Artificial Intelligence in Engineering, vol. 4, no. 2, pp. 112–121, Oct. 2023, doi: 10.21595/jmai.2023.23600.

Copy IEEE

Copied to clipboard!

Liu, Zecheng, Jianyu Chu, and Jinjian Du. “The Optimization Model of Whole Process Engineering Consulting Consortium Members Based on Z-Number.” Journal of Mechatronics and Artificial Intelligence in Engineering 4, no. 2 (October 30, 2023): 112–21. https://doi.org/10.21595/jmai.2023.23600.

Copy Chicago

Copied to clipboard!

The optimization model of whole process engineering consulting consortium members based on Z-number

Abstract

Highlights

1. Introduction

2. The whole process of project consulting consortium member selection index system

2.1. Index weight determination

3. Whole process engineering consulting consortium member selection model

3.1. Modeling idea

3.2. Z-numbers obtaining and processing data

3.2.1. The transformation of language variables

3.2.2. Z-Numbers are converted to classical fuzzy numbers

3.3. Expert weight calculation

3.4. TOPSIS determines the member ordering

4. Example

4.1. Determine index weight

4.2. Evaluation and scoring

4.3. Z-numbers transform

4.4. Calculated expert weight

4.5. TOPSIS calculates the rankings

5. Conclusions

References

Cited by

About this article

Related Articles