An analysis for support loss of micro-cantilever beam based on PML method

1. Introduction

Atomic force microscope (AFM) is a fundamental tool used for research in microscopic fields and is an important member of the huge family of scanning probe microscopes [1], whose emergence has promoted the development of nanotechnology and micro/nano industry, prompting widespread attention from both the scientific and industrial communities. Its core component, the probe, is mechanically described as a micro-cantilever beam, a typical resonant device. And for the AFM probe, energy dissipation is one of the most important issues in the design, because the lower energy dissipation means better performance [2]. Therefore, in order to obtain optimized resonant performance, we must carefully study the dissipation mechanism of the system.

The AFM has various energy dissipation mechanisms, one of which is support loss. It is the phenomenon whereby the energy generated by the vibration of a cantilever beam is propagated through an elastic wave to the support structure and dissipated. Since the support loss is coupled with other dissipations, it is difficult for the experimental operator to verify it experimentally. Therefore, we intend to investigate it by means of finite element simulation. However, we need to consider the fact that in practice the AFM probe is really tiny compared to the support substrate and the support part of the resonator can be modelled as a semi-infinite space. In order to model this, it is necessary to add artificial absorption boundaries in the finite region. There are various types of absorption boundary conditions, such as boundary dampers, infinite elements, boundary integrals and Perfectly Matched Layer (PML) [3-5]. Among these boundary conditions, PML has the advantages of easy implementation, low economic cost, easy calculation, and theoretically can absorb any incident angularity wave [6], [7]. So, in this paper, we choose PML as the boundary condition and use it to investigate the contribution of support loss to the overall system.

Previous studies on support loss have made some achievements. Jimbo and Itao [8] derived an expression of support loss in first-order resonance for a cantilever resonator with infinite out-of-plane thickness attached to a semi-infinite medium. Park et al. [9], [10] proposed a computational model for wave propagation from a vibrating beam to the substrate. Hao et al. [11] derived a closed expression for the support loss in resonant beams. They calculated the support loss of the clamped-free beam and clamped-clamped beam. Cross et al. [12] studied the elastic wave transmission at the joint between two plates of different widths but with the same out-of-plane thickness. Photiadis et al. [13], [14] analyzed the support loss in two different cases, one where the support is treated as a plate of approximate thickness to the resonator, and the other where the support is treated as a semi-infinite elastic medium with an effectively infinite thickness. Darvishian et al. [15] investigated the effect of different modes on the support loss by means of simulations. Li et al. [16] proposed a method to choose optimal parameters to study the support loss.

In this paper, we established a model to simulate the infinite domain using PML, and discussed the theoretical solutions of different researchers for the support loss. After that, we verified the theoretical models by means of two-dimensional (2D) and three-dimensional (3D) finite element simulation. Then we analyzed the effects of micro-cantilever beam size and support medium substrate height to the quality factor of support loss. In addition, we also compared the results of support loss in 2D and 3D models, and proved that the 3D model is closer to the real situation. Finally, for the realistic case of AFM, we estimated the magnitude of the contribution to the system quality factor caused by support loss, and gave some approaches to reduce the dissipation.

2. Theoretical quality factor of support loss

Regarding the theoretical derivation of the support loss, Jimbo and Itao [8] first derived a two-dimensional model’s representation. They compared the energy of the vibration of the cantilever beam with the energy associated with the strain in the elastic medium caused by the shear force and bending moment at the root of the cantilever beam. The expression of quality factor can be obtained as:

where $h$ and $l$ are the height and length of the cantilever beam, respectively. $E_s$ and $E$ are the Young’s modulus of the support substrate and the cantilever beam, respectively.

Hao et al. [11] gave a theoretical explanation for the support loss. The propagation of elastic waves excited by the shear stress of the resonant beam in the support structure is described by 2D elastic wave theory. Their model shows that the quality factor of the high mode is lower than that of the low mode, and the expression of the quality factor is given by:

where $\upsilon$ is the Poisson’s ratio, $\psi$ is a coefficient related to the mode displacement, and $\beta$ and $\chi$ are the mode constant and mode shape factor. This analytical equation has been simplified by Chouvion [19].

Photiadis et al. [13], [14] analyzed the vibration of two different support substrate forms. When the substrate is the support of a semi-infinite plate, the quality factor caused by the out-of-plane vibration of the cantilever beam and radiation to the support substrate is:

where $b$ is the width of the cantilever beam, $h_{\mathrm{s}}$ is the height of the support substrate.

When the support structure is thick enough with respect to the wavelength of the propagating wave, we can approximate the substrate as a semi-infinite elastic medium and obtain the quality factor of the support loss as:

With several equations above, it can be seen that the support loss is closely related to the cantilever beam size and the thickness of the support substrate. The AFM probe in the real state is a typical micro-cantilever vibration system, and the support loss is an important part of the energy dissipation. So it is necessary to explore the dissipation relationship between the support substrate and the micro-cantilever beam.

3. Simulation

3.1. 2D simulation model

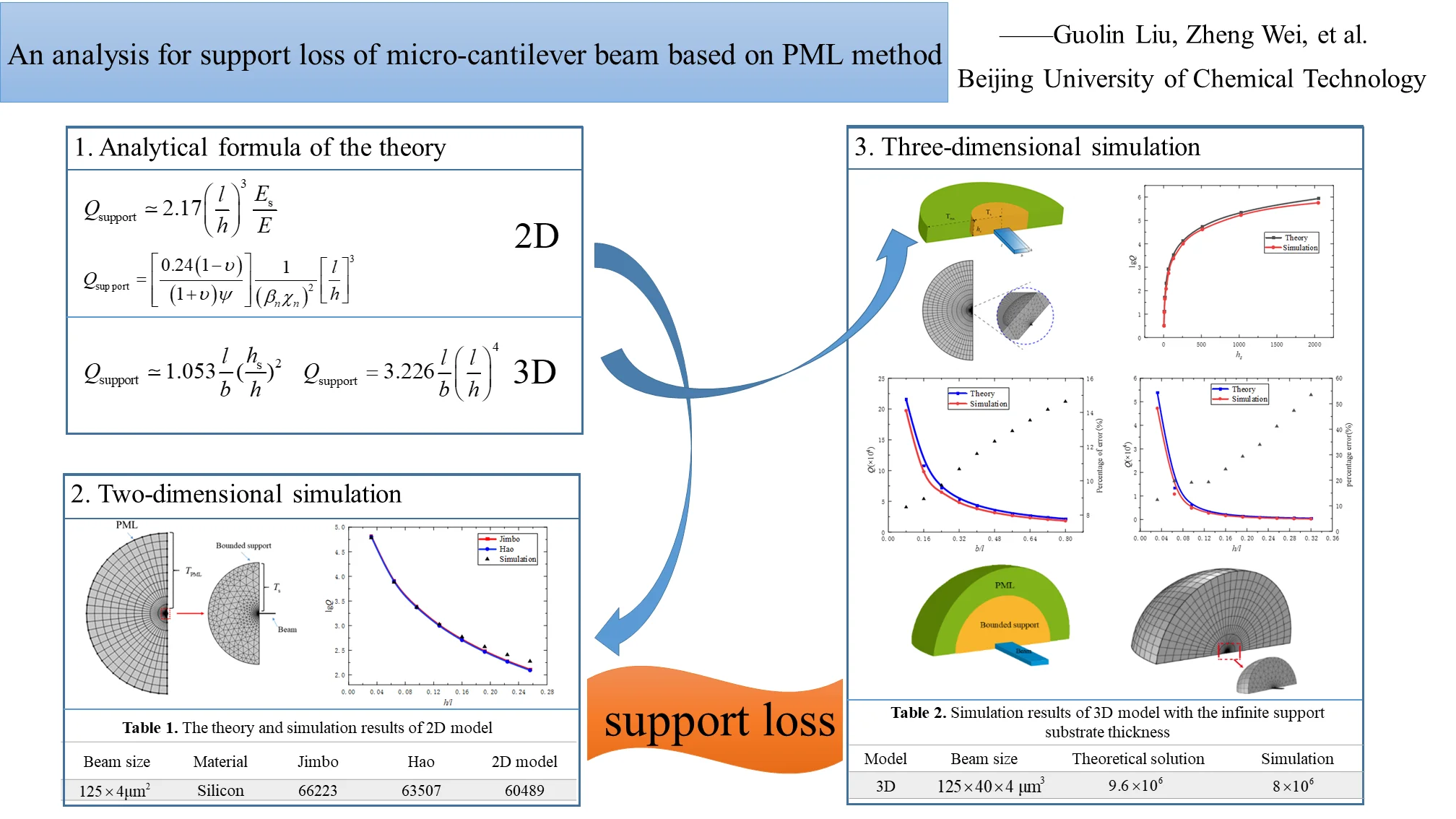
In order to study the contribution of the support loss during the operation of the AFM system and to verify the correctness of the above analytical equations, the method of finite element simulation is used. Considering the actual AFM probe, the probe is very tiny compared to the support substrate, and the support substrate can be approximated as a semi-infinite elastic medium. So, we use PML as the absorbing boundary condition for the model. About the model size, for the actual AFM probe, the size range is between tens of microns. We choose the micro-cantilever beam with the length and height dimensions of 125×4 μm², and the materials of both the beam and the substrate are chosen as silicon, setting the material parameters during the simulation, density $\rho =$2330 kg/m³, Young’s modulus $E=$ 169 GPa, Poisson’s ratio $\upsilon =$ 0.3. The schematic diagram of the model is shown in Fig. 1. The substrate is divided into two parts, the bounded region and the perfectly matched layer. The size of the bounded support region is chosen as $T_{\mathrm{s}}=0.1l^2/h$ and the thickness of the perfectly matched layer is$T_{PML}=0.1{\lambda }_L$ , where ${\lambda }_L$ is the wavelength of the longitudinal wave in the medium.

After completing the simulation model, we were able to obtain the variation of quality factor in the 2D model. The simulation results and the theoretical analysis values in the fundamental frequency of the beam were obtained as shown in Table 1. From the table, we can see that the quality factor value of the 2D model is 60489, and the quality factors calculated by the analytical theories of Jimbo et al. and Hao et al. are 66223 and 63507, respectively. The theoretical and simulation results are in good agreement, verifying the feasibility and accuracy of the simulation with PML.

After that, we consider changing the dimensions of the micro-cantilever beam to investigate the support loss. In the 2D model, by keeping the length constant and changing the height of the cantilever beam, the simulation results are compared with the theoretical results as shown in Fig. 2. From the figure, we can see that the results of the 2D simulation are in good agreement with the theoretical solution. At the same time, according to the change pattern of the curve, we can find that the quality factor of the cantilever beam decreases sharply with the increase of $h/l$, and the support loss become larger. The increase of $h/l$ means that the cantilever beam becomes shorter and thicker, i.e., the cantilever beam has a bigger stiffness. And we can also see that the error between the theoretical value and the simulation result gradually increases with the increase of $h/l$, which is due to the fact that when the structure of the beam becomes shorter and thicker, the more it does not match with the assumption of Euler Bernoulli beam.

Table 1The theory and simulation results of 2D model

Beam size ($l\times h$)	Material	Jimbo et al. [8]	Hao et al. [11]	2D simulation
125×4 μm2	Silicon	66223	63507	60489

Fig. 1Schematic diagram of the two-dimensional model

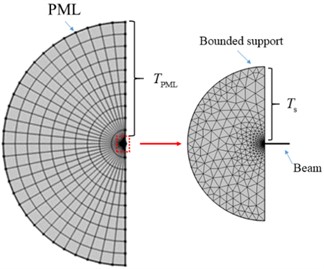
Fig. 2Comparison of simulation and theoretical results of micro-cantilever beam under different h/l

3.2. 3D simulation model

In this section, we consider the simulation of the 3D model. The 3D model has two differences compared with the 2D model. One is that the beam of the 3D model has a finite width, and the second is that the support substrate considered in the 2D model has an infinite thickness, while the 3D model needs to consider the substrate thickness as a finite value. Therefore, for the simulation calculation of the 3D model, it is necessary to set a suitable width size for the cantilever beam. Generally, the width of the AFM probe is in tens of microns, which is taken as 40 μm here, while the support medium substrate is considered to have a finite height of $h_s$, and other parameter settings are the same as the 2D model. The schematic diagram of the model and the meshing diagram are obtained as shown in Fig. 3.

Fig. 3Schematic diagram of the support loss model and simulation mesh

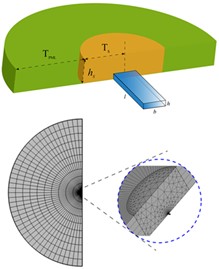
Fig. 4Quality factor at different support substrate heights

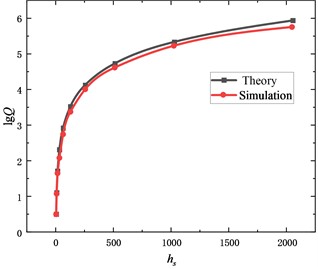
First of all, we consider the effect of the height of the support substrate. We can obtain the quality factors of the micro-cantilever beam in the fundamental frequency state as shown in Fig. 4. From the Fig. 4, it can be seen that the results of the simulation are in good agreement with the theory, and the magnitude of the quality factor is around 10 when the difference between the height of the support substrate and the height of the micro-cantilever beam is small. After that, with the height of the support substrate increasing, the smaller the energy dissipation generated by the micro-cantilever beam through the support loss, the larger the quality factor, and the magnitude can reach 10⁶. This means that the quality factor of the system changes dramatically. Meanwhile, for a typical AFM probe, the height of the support substrate is about $h_{\mathrm{s}}=$ 400 μm, then from the figure, we can see that the quality factor can reach 10⁴.

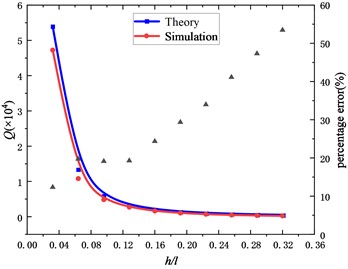
In addition to the support substrate height, this paper also analyzes the effect of micro-cantilever beam dimensions on the support loss, keeping the support substrate height constant, with the cantilever beam width and height as variables, respectively. The results obtained from the simulation are shown in Fig. 5 and Fig. 6. These figures show the effects of the width and height of the micro-cantilever on the quality factor. The variation patterns of both plots are in accordance with Eq. (3), but the errors of the simulations increase as the dimension increase. Fig. 5 shows that the quality factor decreases as the width-to-length ratio increases. While Fig. 6 shows that the quality factor decreases as the height-to-length ratio increases, the error between the theoretically calculated value and the simulation results increases. This also occurs when 2D simulations are performed. It means that Eq. (3) is only valid when the beam structure could be well described by Euler Bernoulli theory.

Fig. 5Quality factor values at different b/l

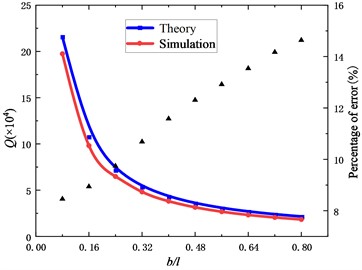
Fig. 6Quality factor values at different h/l

Above we discussed the relationship between the support loss of the AFM and the cantilever beam size. Here, we compare it with the 2D model, assuming that the support substrate has an infinite thickness. In order to achieve this purpose, the model was built as a 1/4 sphere with the outer layer wrapped by an absorbed layer of PML and a bounded support region in the middle. The model parameters were the same as above, and the material of the beam and support substrate was also chosen as silicon. The diagram is shown in Fig. 7.

Fig. 7Infinite thickness support substrate and mesh division schematic

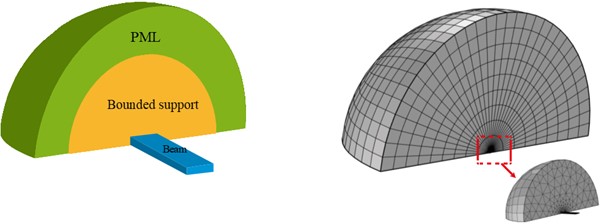
Table 2Simulation results of 3D model with the infinite support substrate thickness

Model	Beam size	Theoretical solution	Simulation
3D	125×40×4 μm2($l\times b\times h$)	9.6×106	8×106

Based on the model described above, we can get a result which shows that the simulation results are approximately consistent with the theoretical analysis. The obtained results were shown in Table 2. Comparing it with the 2D model, we can see that the results of the 2D model and the 3D model have orders of magnitude difference. In the 2D model, the order of magnitude of the support loss with infinite support medium thickness is 10⁴, while in the 3D model the order of magnitude result is 10⁶. Considering the AFM probe in the real state, there is generally an exact width rather than ignoring the model width to approximate it as a 2D problem, and our simulation results in Fig. 5 also confirm that the cantilever beam width does have an effect on the quality factor of the support loss. Thus, we believe that the results calculated by the 3D model are more consistent with the actual situation.

In summary, through the simulation analysis of the 3D model, we have clarified the effect of the support substrate and cantilever beam dimensions on the support loss. Therefore, according to the above laws, in order to reduce the support loss, we can consider increasing the height of the support medium substrate, or changing the cross-sectional shape and dimensional parameters of the cantilever beam. And it can be seen from the Eq. (1) that using the micro-cantilever beam with lower Young's modulus is also a feasible approach.

4. Conclusions

Support loss exists in a variety of different micro- and nano-resonant devices, and it is almost impossible to experimentally measure the contribution of the support loss due to the coupling of the support loss with other dissipation mechanisms. Most of the existing studies on support loss have been analyzed at the theoretical level. Here, through our calculations, the support loss mechanism has a more intuitive representation, which is important for us to reduce the support loss and improve the quality factor of the system.

In this work, a simulation model using PML to simulate the infinite domain is developed and used to investigate the support loss of resonators. The simulation results are given in terms of 2D and 3D models, respectively. From the results, it can be seen that the simulation values are in good agreement with the theoretical values, which proves the feasibility and accuracy of our constructed model. Then, the simulation results of 2D model and 3D model were compared, and it was clear that the results calculated by 3D model were more consistent with the actual situation. Meanwhile, based on this, we investigated the contribution of support substrate thickness and micro-cantilever beam size to the support loss, which showed that the thicker the support substrate and the slimmer the beam, the smaller the support loss. According to this, in order to reduce the support loss, we can consider both of increasing the height of the finite support substrate or changing the dimensional parameters of the micro-cantilever beam. Finally, for the typical AFM, we estimate the quality factor caused by the support loss to be 10⁴.