Analysis of a bus vertical dynamic performances – a comparison between linear and nonlinear suspension systems

2.1.1. The quarter-car dynamic 2DOF model

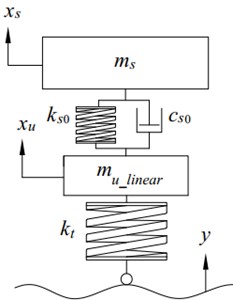
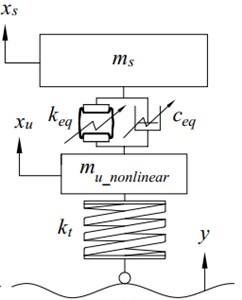
The quarter-car vertical dynamic 2DOF model with two types of linear and nonlinear suspension systems is employed to determine the vertical dynamic evaluation indexes of a bus, Fig. 1.

Fig. 1The quarter-car dynamic 2DOF model: a) linear, b) nonlinear

a)

b)

The model allows to determine the vertical dynamic evaluation indexes of the ride comfort, suspension working space, and road holding. The model consists of two elements of an un-sprung mass and a sprung mass, all moving vertically. The excitations are considered for all three types of harmonic, transient and random.

The symbols and input calculation parameters are determined and selected based on a typical bus in Vietnam. The symbols and the meaning of the quarter-car dynamic 2DOF model parameters are given in Table 1.

The differential equation describing vertical dynamic motion, with a vector of state variables, $X={\left[\begin{array}{ll}{x}_u& x_s\end{array}\right]}^{\mathrm{\text{'}}}$ is written in matrix form, Eq. (1):

The mass matrix [$m$], in which the un-sprung mass $m_u$ in the case of nonlinear suspension has a value reduced by 20 % compared with the case of the linear suspension, Table 1. The stiffness matrix [$k$] with instantaneous nonlinear air spring stiffness $k_{eq}$ is used in the case of nonlinear suspension. In the case of linear suspension, the spring stiffness is selected as the air spring stiffness at the initial equilibrium position $k_{s0}$, [11].

The damping matrix [$c$] with instantaneous damping coefficient of the asymmetrical nonlinear shock absorber $c_{eq}$ is used in the case of nonlinear suspension. In the case of linear suspension, the damping coefficient is selected as the initial damping coefficient $c_{s0}=$6500 (Ns/m), corresponding to the damping ratio value $\xi =$0.3, [10, 12].

The excitation force vectors [$F$] are in the form of harmonic, transient, and random. The matrices included in the general dynamic equation are presented as follows, [9, 10]:

With linear suspension case:

With nonlinear suspension case:

2.1.2. Spring stiffness

The nonlinear suspension system includes an air spring, the corresponding stiffness, $k_{eq}$ by 3rd order polynomial interpolation based on the calculated instantaneous displacement value relative to the initial equilibrium position of the air spring corresponding to its extension or compression stroke [11]. The characteristic curves of the experimental stiffness and the interpolated ones according to the 3rd order polynomial versus the displacement around the equilibrium position is shown in Fig. 2. For a linear suspension, the spring stiffness parameter is selected as the air spring stiffness value at the initial equilibrium position $k_{s0}$, which is equivalent to a natural frequency close to 1 (Hz), the usual natural frequency of common vehicles’ suspension systems [12]. The limited working stroke of the air spring is ±0.1 (m).

Fig. 2Equivalent stiffness versus displacement of the air spring, experimental and polynomial interpolation

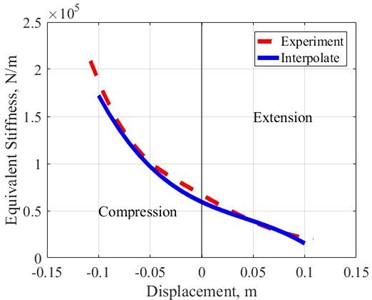
Fig. 3Variation characteristics of the equivalent damping force versus velocity

2.1.3. Damping coefficient

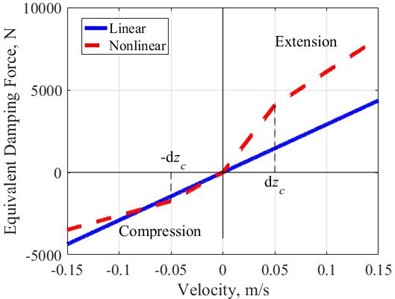
The Nonlinear Asymmetric (NA) shock absorber model is employed to perform the calculation, [10, 11]. In the initial condition, the equivalent damping coefficient $c_{eq}$ is equal to $c_{s0}$, when the damping force is equal to zero, $F_{eqD}=$0. When the system is subjected to an external applied loading, $F_{eqD}\ne$0, $c_{eq}$ is determined by the equivalent damping force $F_{eqD}$, suspension relative velocity, and the shock absorber’s state of stroke. The selected asymmetry coefficient corresponding to the asymmetry ratio of 30/70 is $e_D=$0.4, [13]. The equivalent damping coefficient changes when the relative velocity $dz$ reaches the knee-point critical value $d{z}_c=$0.05 (m/s), with coefficients $\kappa =$1, $\lambda =$2. The equivalent damping force is calculated according to Eq. (2), [10, 11]:

The characteristic curves of equivalent damping force, $F_{eqD}$ versus the relative velocity $dz$, for the case of linear and nonlinear shock absorbers, are shown in Fig. 3.

2.3.1. Body vibration acceleration – BVA

The gain response of BVA index in the case of harmonic excitation is defined as the ratio of the acceleration amplitude to the applied acceleration amplitude, [10, 14], according to Eq. (5):

Under transient excitation, the maximum of BVA in the time domain is determined by Eq. (6), [18]:

Under random excitation, the ISO-2631 is employed to account for frequency-weighted effects, [19]. The RMS of the frequency weighted acceleration is defined by Eq. (7), [20]:

2.3.2. Suspension dynamic deflection – SDD

The gain response of SDD index in the case of harmonic excitation is defined as the ratio of the relative displacement amplitude to the applied amplitude, [14], Eq. (8):

The maximum of SDD index in the time domain is determined in the case of transient excitation, Eq. (9), [18]:

In the case of a random excitation, the RMS of SDD is determined by Eq. (10), [20]:

2.3.3. Tire dynamic load – TDL

The maximum TDL index is determined in both the case of harmonic and transient excitations, Eq. (11), [18]:

In the case of the random excitation, the RMS of TDL is determined by Eq. (12), [20]:

4.1.1. BVA

Under harmonic excitation, the $G_{BVA}$ in the frequency domain is determined by Eq. (5), Fig. 5. At the natural frequency of the suspension, the obtained $G_{BVA}$ reach the peak values. The $G_{BVA}$ peak value with nonlinear suspension is less about 10 % than that of the linear suspension. Because the nonlinear suspension has a higher damping coefficient in the low velocity region corresponding to low frequencies, [10].

Outside the suspension resonant frequency range, the $G_{BVA}$ values of the two types of suspension systems are almost equal. In addition, in the frequency region higher than 5 (Hz), especially at the frequency around 11 (Hz) which is the resonance region of the tire, the $G_{BVA}$ with nonlinear suspension is slightly less than the linear one. Therefore, the nonlinear suspension helps to improve the ride comfort at the resonance frequencies of both the suspension and tire.

Fig. 4Calculation flowchart

4.1.2. SDD

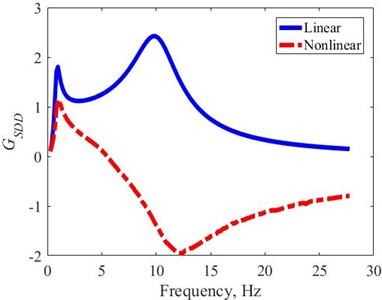
The $G_{SDD}$ are determined by Eq. (8) and shown in the frequency domain, Fig. 6. The obtained $G_{SDD}$ with linear suspension is always positive and reaches the two peaks at the corresponding resonances of the suspension and tire natural frequencies. The natural frequency of a tire with a nonlinear suspension is slightly higher than that of a linear suspension. Because the unsprung mass of the nonlinear suspension is 20 % less than that of the linear suspension. However, the obtained $G_{SDD}$ with nonlinear suspension has a positive value at the resonance of suspension and is much lower than that of a linear suspension. In addition, when the excitation frequency is larger than 5 (Hz), the $G_{SDD}$ decreases rapidly and has a negative value. At the resonant frequency of the tire, the $G_{SDD}$ reaches the second peak. Due to the asymmetrical characteristic of the nonlinear suspension, both of damping coefficient and spring stiffness are lower in the state of compression. The asymmetry around the zero axis of the suspension relative displacement causes the big difference in the $G_{SDD}$ between the linear and nonlinear suspension systems as shown in Fig. 6, [10]. Therefore, the nonlinear suspension is in a compressed state when the excitation frequency is larger than 5 (Hz), corresponding to the vehicle’s center of gravity tends to lower, increasing the dynamic stability in operation.

Fig. 5Gain response of BVA in the frequency domain – harmonic excitation

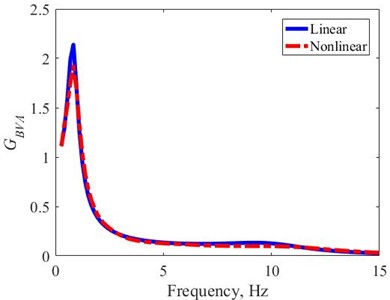
Fig. 6Gain response of SDD in the frequency domain – harmonic excitation

The dynamic working stroke of the nonlinear suspension is asymmetric around the initial equilibrium position. To compare the suspension dynamic deflection stroke (SDDS) of linear and nonlinear suspension, the gain response of SDDS is defined by Eq. (13):

The obtained $G_{SDDS}$ in the frequency domain, Fig. 7, shows that the two peaks at the two corresponding resonant frequencies are always smaller than with the nonlinear suspension. In addition, $G_{SDDS}$ with nonlinear suspension is always less, when the excitation frequency is less than 11 (Hz). Conversely, $G_{SDDS}$ with nonlinear suspension is larger when the excitation frequency is larger than 11 (Hz). Therefore, with the higher excitation frequency, $G_{SSDS}$ with the nonlinear suspension will be higher than that of the linear suspension and vice versa.

4.1.3. TDL

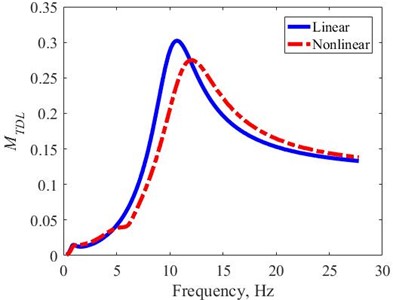
The obtained $M_{TDL}$ in the frequency domain under the harmonic excitation is determined by Eq. (11), Fig. 8. The obtained $M_{TDL}$ allows to evaluate the road holding feature of the vehicle, the larger the $M_{TDL}$ the lower the road holding or the vehicle will have less stability. The $M_{TLD}$ reaches its peak at the natural frequency resonant of the tire, with the nonlinear suspension having the peak reduced by 7 % compared to the linear suspension. Furthermore, the peak of $M_{TDL}$ is obtained at higher frequency with nonlinear suspensions, since the unsprung mass is 20 % less than with linear suspensions. When the excitation frequency is less than 11 (Hz), the obtained $M_{TLD}$ with nonlinear suspension is always smaller than with linear suspension. Conversely, when the excitation frequency is larger than 11 (Hz), the obtained $M_{TDL}$ with nonlinear suspension is slightly larger than with linear suspension.

In summary, under the harmonic excitation with a frequency less than about 11 (Hz), which is the natural frequency of the tire, with nonlinear suspension, we always obtain the better corresponding acceleration, displacement, and TDL indexes, which are used to evaluate the vertical dynamic performance of ride comfort, suspension working space, and road holding. Especially, the peaks of these evaluation indexes at the resonance of the suspension and tire natural frequencies are always significantly smaller than those of the linear suspension. However, in contrast, in the excitation frequency domain larger than 11 (Hz), the obtained evaluation indexes show that the linear suspension gives slightly better results than the nonlinear suspension.

Fig. 7Gain response of SDDS in the frequency domain – harmonic excitation

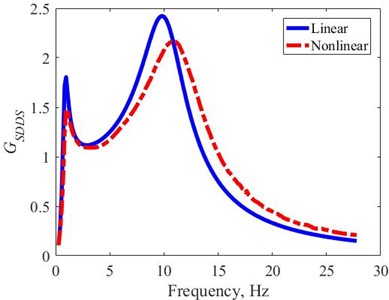
Fig. 8MTDL in the frequency domain – harmonic excitation

4.2.1. BVA

The obtained $M_{BVA}$ under transient excitation in the velocity domain is determined by Eq. (6), Fig. 9. The obtained results show that the $M_{BVA}$ increases linearly in the velocity domain, and for nonlinear suspension is always slightly larger than linear suspension. Therefore, the ride comfort of the bus with the linear suspension is slightly better than that of the nonlinear suspension. In the velocity domain larger than 20 (m/s), the obtained $M_{BVA}$ show that the linear suspension gives rapidly better results than the nonlinear suspension.

Fig. 9MBVA in the velocity domain – transient excitation

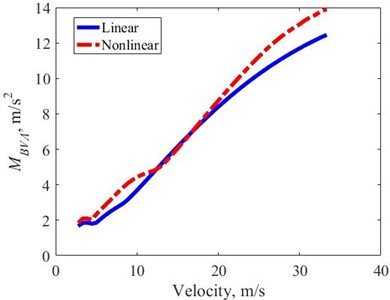
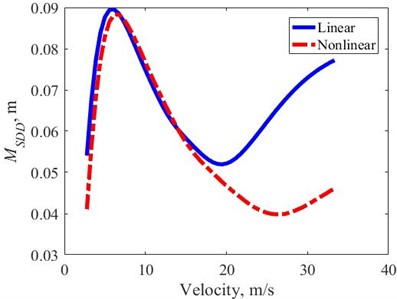
Fig. 10MSDD in the velocity domain – transient excitation

4.2.2. SDD

The obtained $M_{SDD}$ under transient excitation, in the velocity domain is defined in terms of Eq. (9), Fig. 10. The results show that $M_{SDD}$ increases rapidly with velocity and reaches a large value in the velocity range from 5-10 (m/s), then decreases rapidly in the velocity range from 10-20 (m/s), and in the velocity range from 5-15 (m/s) the obtained $M_{SDD}$ is almost equal with two types of linear and nonlinear suspension. In contrast, when the velocity is greater than 20 (m/s), the $M_{SDD}$ with the nonlinear suspension continues to decrease rapidly and increase slightly when the velocity reaches 25 (m/s). The $M_{SDD}$ increases rapidly with the linear suspension, at the velocity 33 (m/s), the $M_{SDD}$ with linear suspension is 67 % larger than that of the nonlinear suspension.

Therefore, as subjected under transient excitation in the type of IRC, the obtained $M_{SDD}$ with two types of nonlinear and linear suspension systems are almost equal at velocity values less than 20 (m/s). However, in contrast to the velocity domain greater than 20 (m/s), $M_{SDD}$ with nonlinear suspension is much smaller than linear suspension. With nonlinear suspension, the evaluation index of suspension working space is much better than linear suspension. It means that the dynamic stability increases significantly under sudden changes in the applied loadings [11].

Similar to Section 4.1.2, the working stroke of the nonlinear suspension is asymmetric around the initial equilibrium position. In order to be able to compare suspension dynamic deflection stroke (SDDS) of linear and nonlinear suspensions under transient excitation, the SDDS is defined by Eq. (14). In the Fig. 11, the obtained SDDS with nonlinear suspensions is always smaller than linear ones, at maximum velocity up to 16 % smaller value. Therefore, under the effect of transient excitation, the nonlinear suspension system has a better suspension working space evaluation index than the linear system.

Fig. 11SDDS in the velocity domain – transient excitation

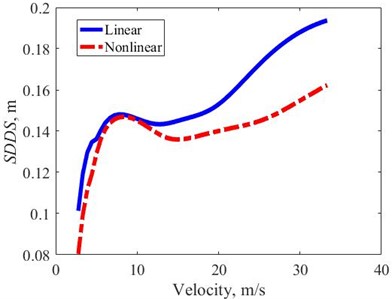
Fig. 12MTDL in the velocity domain – transient excitation

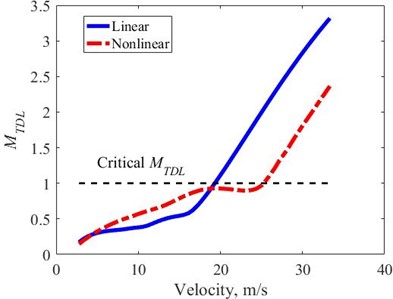
4.2.3. TDL

The obtained $M_{TDL}$ under transient excitation is determined by Eq. (11), Fig. 12. The $M_{TDL}$ helps to evaluate the road holding feature of the vehicle, the larger the $M_{TDL}$the lower the road holding feature. The critical value of $M_{TDL}$ is equal to 1, the wheel is no longer hold to the road surface, correspondingly. The results show that, in the velocity domain less than 20 (m/s), the obtained $M_{TDL}$ with both linear and nonlinear suspension systems has a value of less than 1, or the wheel is still hold to the road, and $M_{TDL}$ with linear suspension is always slightly smaller than nonlinear suspension, or wheels have better road holding with linear suspension in the low velocity range. However, $M_{TDL}$ reaches its critical value earlier with linear suspension at velocity close to 20 (m/s), whereas with nonlinear suspension $M_{TDL}$ reaches its critical value at higher velocity of about 25 (m/s). Thus, with the nonlinear suspension the velocity value at which the $M_{TDL}$ reaches its critical point is larger than that of the linear suspension. With the nonlinear suspension system, the road holding feature has been improved, in particular, the critical velocity of road holding is increased compared to the case of a suspension with only asymmetric shock absorber [9].

4.3.1. BVA

The obtained $R_{BVAw}$ under the excitation of random class A is determined by Eq. (7), in which the $BVAw$ includes frequency weighting according to ISO-2631, Fig. 13. The results show that, for both linear and nonlinear suspension systems, the obtained $R_{BVAw}$ are all smaller than the fairly uncomfortable level, 0.63 (m/s²) according to the ISO-2631 standard, in the entire observed velocity domain. In the velocity range from 10-25 (m/s), $R_{BVAw}$ has a larger value than the rest of the velocity range. When the velocity is less than 20 (m/s), the $R_{BVAw}$ with the two types of suspension is almost the same. However, when the velocity is larger than 20 (m/s), the obtained $R_{BVAw}$ with nonlinear suspension is about 40 % on average larger than with linear suspension. Therefore, ride comfort with both suspension types is almost the same in the low velocity domain, and ride comfort is significantly better with linear suspension in the velocity range larger than 20 (m/s).

Fig. 13RBVAw in the velocity domain – random excitation

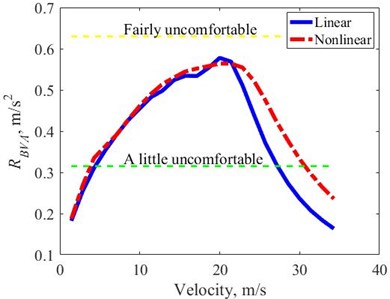
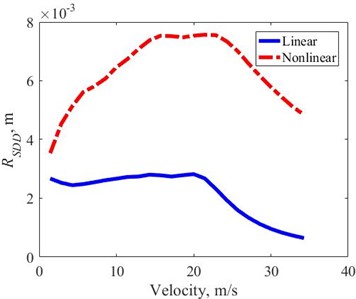
Fig. 14RSDD in the velocity domain – random excitation

4.3.2. SDD

The obtained $R_{SDD}$ under random excitation is determined by Eq. (10), Fig. 14. The results show that the obtained $R_{SDD}$ with nonlinear suspension is much larger than with linear suspension in the whole observed velocity domain. However, under random excitation, the road bump amplitude is not high compared to the case of transient excitation. Therefore, in general, it can be seen that with nonlinear suspension, the $R_{SDD}$ index is not quite enough to be used to evaluate the suspension working space feature as the obtained $M_{SDD}$ index in the case of transient excitation in Section 4.2.2 above.

In addition, the nonlinear suspension under road excitation has the working state mostly in the compression state and the working stroke is asymmetric compared to the initial equilibrium position. It causes the big difference in the $R_{SDD}$ between the linear and nonlinear suspension systems as shown in Fig. 14. Or the vehicle's center of gravity will be lowered compared to the original during operation on the road. Similar to the Sections 4.1.2 and 4.2.2, in order to be able to compare the SDDS of linear and nonlinear suspension, the RMS of SDDS is defined by Eq. (15), where the RMS is calculated with the parameter being the difference of the relative displacement over time and its mean:

The obtained $R_{SDDS}$ under random excitation is determined by Eq. (15), where the SDDS is taken into account the asymmetrical working stroke of the nonlinear suspension, Fig. 15. The results show that, the obtained $R_{SDDS}$ with linear suspension is not changed since the suspension working stroke is symmetric relative to the initial equilibrium position, or the mean of the linear suspension relative displacement is close to zero. With nonlinear suspension, the obtained $R_{SDDS}$ is slightly smaller than linear suspension in the velocity domain less than 20 (m/s). However, for the velocity domain larger than 20 (m/s), the obtained $R_{SDDS}$ with the nonlinear suspension is slightly larger than that of the linear suspension, similar to the obtained results of $R_{BVAw}$, as in Fig. 13.

Therefore, under random excitation, a bus with a nonlinear suspension will have a slightly lower center of gravity and a slightly smaller working stroke than a linear suspension in the low velocity region. And conversely, in the velocity domain larger than 20 (m/s), the nonlinear suspension will have an average working stroke up to about 65 % larger than the linear suspension. Generally, the suspension working space evaluation index of the nonlinear suspension is slightly better than that of the linear suspension in the low velocity domain. However, in contrast in the velocity domain larger than 20 (m/s), the suspension working space evaluation index is significantly better with linear suspension.

Fig. 15RSDDS in the velocity domain – random excitation

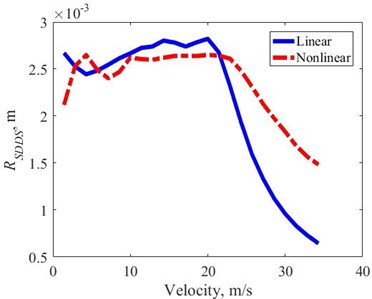
Fig. 16RTDL in the velocity domain – random excitation

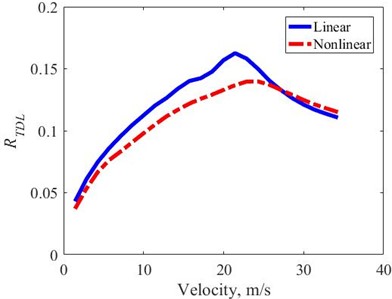
4.3.3. TDL

The obtained $R_{TDL}$, under random excitation is determined by Eq. (12), Fig. 16. The results show that the obtained $R_{TDL}$ with the nonlinear suspension is always about 8 % better on average than the linear suspension in the whole observed velocity domain. The maximum of $R_{TDL}$ are achieved with linear suspension at 20 (m/s), and with nonlinear suspension at 25 (m/s). The two velocity values, at which the maximum $R_{TDL}$ are obtained with both types of suspensions, are respectively equal to the two values of the critical velocity under transient excitation, Fig. 12. Thus, the road holding with nonlinear suspension improved on average by about 8 % in the lower velocity region, with a larger velocity range than 25 (m/s) this index with both suspension types being the same.