Torsional dynamics and parametric instability in integrated electric drive systems with PMSM and gear train

1. Introduction

The gear train within the reducer achieves speed reduction, converting the high-speed rotation of the motor or other power source into low-speed, high-torque output. It is widely used in fields such as automotive, construction machinery, and aerospace. The integration of the reducer and motor can reduce weight and volume of the system, lower manufacturing costs, and enhance power density. However, this integration also results in complex torsional vibrations due to the coupled excitation of electromagnetic forces and gear meshing. Therefore, studying the vibration characteristics of the integrated system is of significant importance.

Many studies have investigated the vibration response characteristics of gear systems arising from factors such as gear clearances, errors, and time-varying meshing stiffness. Shen et al. [1] developed a dynamic model of a spur gear pair considering time-varying stiffness and clearance, and analyzed the effects of multiple harmonics on periodic solutions using numerical method and the incremental harmonic balance method. Khabou et al. [2] employed the Newmark method to compute the dynamic response, performed a parameter study on spur gears driven by motors and engines, and discussed how speed variations influence the system's vibration characteristics.

Han et al. [3] employed an improved interval harmonic balance method to investigate the dynamics of a single-mesh gear system, incorporating the nonlinear effects of backlash and time-varying meshing stiffness, and examined the influence of parameter uncertainties on the system’s vibration characteristics. Chen et al. [4] developed a nonlinear dynamic model of gear pairs that accounts for microscopic tooth surface features, and analyzed the effects of tooth surface roughness, viscous damping, and meshing stiffness on the dynamic behavior of the gear transmission.

Cao et al. [5] proposed a dynamic model for spur gears considering the influence of load-dependent time-varying meshing stiffness, backlash, and tooth profile deviation. The predicted response of the model was validated against experimental results. To account for axial deviation as an interval parameter in dynamic response analysis, Hu et al. [6] employed an interval analysis method based on the Chebyshev inclusion function to investigate the excitation effect of shaft alignment uncertainty on gear systems.

Extensive research has been conducted on parametric instability in gear systems induced by time-varying meshing stiffness. Parker et al. [7-9] analyzed instability in two-stage gears, planetary gears, and idler gear systems using the asymptotic perturbation method, and revealed the influence of key parameters on the instability regions and vibration response. Rao et al. [10] incorporated both time-varying meshing stiffness and shaft torsional flexibility to investigate torsional instability in a two-stage gear system. The instability regions of the gear system were analyzed using the multi-scale method, and the results were validated through numerical calculations.

Liu et al. [11] developed a dynamic model that accounts for time-varying stiffness of bearings and gear pairs, and investigated the parametric instability induced by the combined fluctuations in stiffness. Gawande et al. [12-13] used a two-stage gear train to identify specific operating conditions leading to parametric instability. The influence of meshing stiffness parameters –including mesh frequency, amplitude of stiffness variation, and mesh phasing contact ratio – on these instabilities was analyzed. The analysis was verified through numerical solution, demonstrating that replacement gear pairs with appropriate mesh phasing can eliminate the instability regions originally present in the two gear pairs of the two-stage gear transmission system. Beinstingel et al. [14] conducted experimental and numerical studies on the vibration behavior of high-speed planetary gearboxes. Using a rotating lumped parameter model with time-varying gear meshing stiffness, they theoretically investigated instability phenomena and experimentally confirmed the occurrence of parametric instability in planetary gearboxes.

Electromechanical coupling and nonlinear effects in permanent magnet synchronous motors (PMSMs) significantly influence NVH performance and operational safety. Chen et al. [15] established a nonlinear PMSM model that accounts for the unbalanced magnetic pull caused by nonuniform magnetic fields, analyzed and obtained approximate solutions to the vibration equation, and discussed the instability characteristics of the system's vibration response. Shin et al. [16] developed an analytical solution for the magnetic field produced by permanent magnets in PMSMs, analyzed electromagnetic vibration sources such as torque ripple, cogging torque, and radial force density, investigated the motor's vibration characteristics and experimentally validated these findings via vibration tests.

Liu et al. [17] developed a rotor-bearing system model considering unbalanced magnetic pull and rotor eccentricity, using multi-scale perturbation methods to study solution instability. Yang et al. [18] used both finite element and analytical methods to investigate the relationship between electromagnetic forces and vibration modes. Wu et al. [19] proposed a multi-physics model to study motor vibration mechanisms and the influence of current harmonics. Sheng et al. [20, 21] established an electromechanically coupled torsional dynamic model for PMSM rotor systems, studied the system using multi-scale and numerical methods.

While significant research efforts have been devoted to individual motor or gear systems, the coupled vibration phenomena in integrated electric drive systems have received comparatively less attention. Hu et al. [22] developed a transient dynamic model of an integrated system comprising a helical gear transmission and a PMSM, and proposed an active vibration reduction strategy to minimize gear mesh force and dynamic load. Yi et al. [23] established a dynamic model of a motor-driven multistage gear system and analyzed the influence of electromagnetic effects on natural characteristics of the gearbox. Liu et al. [24] investigated the effect of load conditions on natural frequency, vibration modes, and motor current in electric vehicle drive systems under electromagnetic excitations.

This paper focuses on the dynamic behavior of integrated system that consists of a permanent magnet synchronous motor (PMSM) and a two-stage gear train. Considering the influence of the torque angle on the motor's back electromotive force, an analytical expression for the electromagnetic torque is derived using energy principles. A nonlinear torsional dynamic model is established that incorporates both the motor and the gear transmission.

The stability of parametric vibrations induced by time-varying meshing stiffness is analyzed using the multi-scale method. The differential equation of the system is solved numerically via the Runge-Kutta method, and the dynamic characteristics of the elastic meshing force are discussed in both the time domain and the frequency domain. The variations of the dynamic load coefficients for each gear pair with respect to excitation frequency are examined, and the relationship between peak positions and the system’s natural frequencies is discussed.

2. Dynamic model of integrated electric drive system

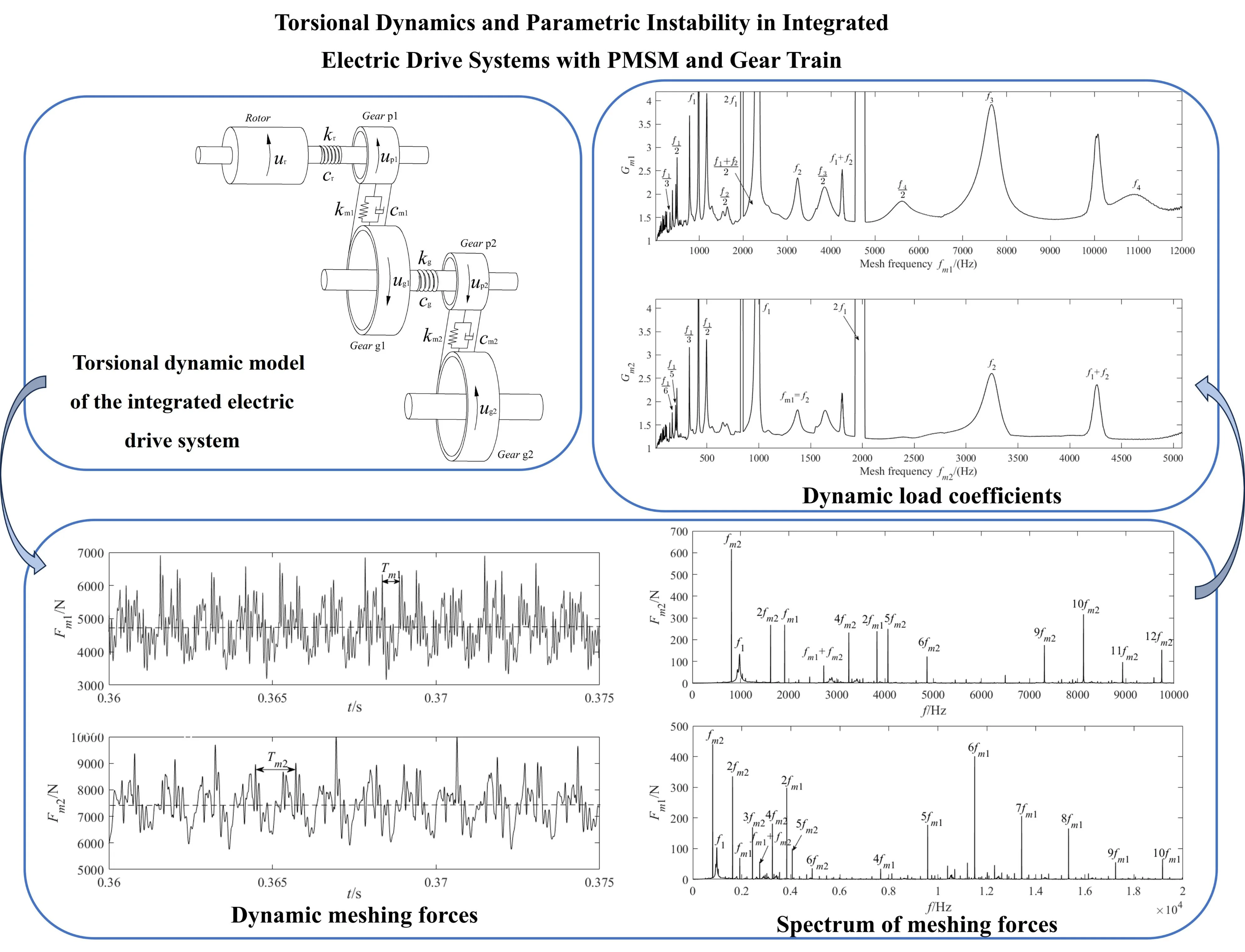
The dynamic model of the integrated electric drive system is composed of a motor module and a gear transmission system module, as illustrated in Fig. 1. Here, the components labeled $r$, $p$ and $g$ represent the rotor of the permanent magnet synchronous motor, the driving gear, and driven gear, respectively. The synchronous motor $r$ operates at high speed, and after passing through the two-stage meshing gear pairs $m_1$ and $m_2$, the driven gear $g_2$ delivers high torque and outputs at low speed.

Assuming that the stiffness of the bearing support is significantly greater than that of the gear pair, only torsional vibrations are considered. The torsional displacement of each component is defined as a generalized coordinate of the system:

In Fig. 1, $k_r$ and $k_g$ represent the torsional stiffness of the motor output shaft and the double gear shaft, respectively, while $k_{m1}$ and $k_{m2}$ represent the mesh stiffness of the two gear pairs. A corresponding convention applies to the damping coefficients, denoted as $c_r$, $c_g$, $c_{m1}$, and $c_{m2}$.

Fig. 1Torsional dynamic model of the integrated electric drive system

3. Equations of motion for the system

The vibration differential equation for the integrated electric drive system is derived as follows:

where, $r_r$ is the radius of the motor rotor shaft; $r_p$ and $r_g$ are the base circle radii of the driving and driven gears, respectively; and $I_h$ (where $h=r,p,g$) represents the rotational inertia of each component. The relative displacements of the gear pair are given by:

Substituting Eq. (14) into Eqs. (13) yields the matrix form of the system's differential equation:

where $M$, $C$, $K$, and $Q$ represent the generalized mass matrix, damping matrix, stiffness matrix, and generalized force vector, respectively. For further details, refer to the Appendix.

4. Decoupling of dynamic equations and stability analysis

Neglecting external excitations and damping, the equation for the system’s free vibration is:

where $K_v\left(t\right)$ is the variable stiffness matrix, and $K_a$ is the average stiffness matrix. By setting $K_v\left(t\right)=0$ in Eq. (16), the system equation simplifies to:

Solving Eq. (17) leads to the eigenvalue problem:

where ${\omega }_i$ and ${\phi }^{\left(i\right)}$ are the $i$-th natural frequency and the corresponding mode vector, respectively. Let:

where $\mathrm{\Phi }=\left[{\phi }^{\left(1\right)},{\phi }^{\left(2\right)},...,{\phi }^{\left(n\right)}\right]$ is the main modal matrix, and $q={\left[x_{q1},x_{q1},...,x_{qn}\right]}^T$ is the generalized coordinate vector. Substituting Eq. (19) into Eq. (16) and left-multiplying by ${\mathrm{\Phi }}^T$, the regular modal equation of the system is obtained:

Expanding Eq. (20) gives:

where ${\epsilon }_m=\frac{k_m^v}{k_m^a}$, and the coefficient terms are expressed as:

Using the multi-scale method, time variables representing different scales are introduced:

where $\epsilon =\mathrm{m}\mathrm{a}\mathrm{x}\left\{{\epsilon }_{m1},{\epsilon }_{m2}\right\}$. The first-order approximation solution of Eq. (21) is assumed as:

Substituting Eq. (23) into Eq. (21), and equating terms of the same power of $\epsilon$ yields:

where $A_n\left(T_1\right)$ is the complex amplitude, and $cc$ denotes the complex conjugate of the preceding term.

Substitution Eq. (24) into Eq. (25) leads to:

From the analysis of the above equation, in addition to the resonance that occurs when the meshing frequency approaches the system’s natural frequency, secular terms arise when $l{\mathrm{\Omega }}_m$ approaches the combination frequencies ${\omega }_n\pm {\omega }_r$. This behavior indicates that the gear system exhibits an instability region due to parametric excitation.

5. Parameter excitation vibration characteristics

The key parameters for the PMSM module and the two-stage gear transmission module, corresponding to the model in Fig. 1, are provided in Table 1 and Table 2, respectively.

The natural frequencies of the integrated electric drive system, calculated from Eq. (17), are given in Table 3.

5.1. Dynamic characteristics of the meshing force

The differential Eq. (13) are solved numerically using the Runge-Kutta method, yielding real-time solutions for each degree of freedom in the system. The meshing force for gear pair $m$ is calculated as follows:

27

$F_m\left(t\right)=k_m\left(t\right){\delta }_m\left(t\right)+c_m\left(t\right){\dot{\delta }}_m\left(t\right),$

where $k_m\left(t\right)$ and $c_m\left(t\right)$ denote the time-varying meshing stiffness and damping coefficients, respectively.

Table 1Parameters of the motor module

Parameters	Values	Parameters	Values
Number of phases	$\mathrm{m}=$ 3	Number of series conductors per phase	$N_w=$ 80
Pole pair number	$p=$ 4	Number of conductors per slot	10
Number of slots	$Z=$ 48	Axial length of stator core (mm)	$l=$ 100
Winding pitch	$y_1=$ 5	Axial length of rotor core (mm)	$l=$ 100
Polar distance	$\tau =$ 6	Remanent magnetic flux density (T)	$B_r=$ 1.097
Rotor inner diameter (mm)	$r=$ 70	Thickness of permanent magnet (mm)	$h_m=$ 5
Rotor outer diameter (mm)	$r=$123.8	Torsional stiffness (N·m /rad)	$k_r=$2.1×105
Stator inner diameter (mm)	$R=$ 125	Width of permanent magnet (mm)	$b=$ 16

Table 2Parameters of the gear transmission

Parameters	Values
Number of teeth	$z_{p1}=\text{23}$, $z_{g1}=\text{59}$, $z_{p2}=\text{25}$, $z_{g2}=\text{89}$
Modulus (mm)	$m_{p1}=m_{g1}=\text{2}$, $m_{p2}=m_{g2}=\text{3}$
Tooth width (mm)	$b_{p1}=\text{30}$, $b_{g1}=\text{30}$, $b_{p2}=\text{30}$, $b_{g2}=\text{30}$
Pressure angle (°)	${\alpha }_{p1}={\alpha }_{g1}=\text{20}$, ${\alpha }_{p2}={\alpha }_{g2}=\text{20}$
Moment of inertia (kg·m2)	$I_{p1}=$ 1.03×10-4, $I_{g1}=$ 2.418×10-3 $I_{p2}=$7.3×10-4, $I_{g2}=$ 7.95×10-2
Mesh stiffness (N/m)	$k_{m1}^{max}=$ 614.68×106, $k_{m1}^{min}=$ 347.83×106 $k_{m2}^{max}=$ 640.77×106, $k_{m2}^{min}=$ 362.96×106
Contact ratio	${ϵ}_{m1}=\text{1.68}$, ${ϵ}_{m1}=\text{1.72}$
Torsional stiffness (N·m/rad)	$k_g=$ 9.0×105

Table 3Natural frequencies of the integrated electric drive system

Order	$f_1$	$f_2$	$f_3$	$f_4$
Frequency (Hz)	1001.15	3293.81	7868.40	11122.03

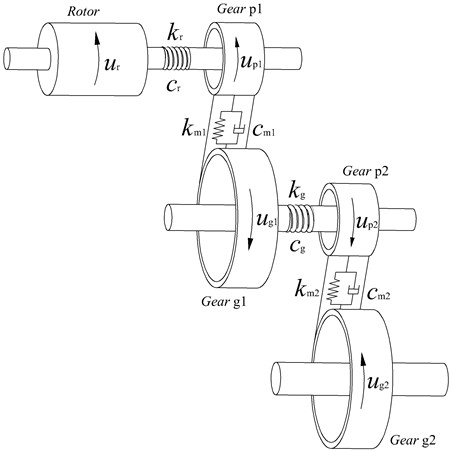
Under constant torque conditions and with the motor speed maintained at $n_r=$ 5000 r/min, the variation of meshing force with time is illustrated in Fig. 2. The dynamic meshing force oscillates around the static meshing force value, represented by the dashed line. Furthermore, high-frequency fluctuations with small amplitudes are observed within each meshing cycle, which are caused by the time-varying stiffness parameters such as the contact ratio.

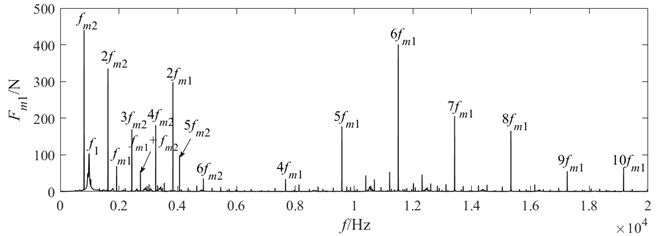
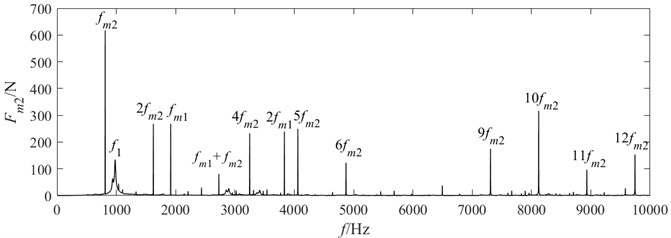
With the torque held constant and the motor speed maintained at $n_r=$ 5000 r/min, the frequency spectrum of the meshing force is shown in Fig. 3. The results indicate that, in addition to the meshing frequency of the current gear pair, the meshing frequencies of the other gear stage, as well as the system’s natural frequencies, are also present in the spectrum of each meshing force. This suggests the occurrence of a coupled multi-frequency vibration phenomenon within the system.

In the frequency spectrum of the meshing force for the high-speed gear pair $m_1$, not only does the low-speed meshing frequency $f_{m2}$ (with relatively higher amplitude) appear, but the system’s natural frequency and the combined frequency $f_{m1}+f_{m2}$ are also present. Similarly, the high-speed stage meshing frequency $f_{m1}$ also appears in the spectrum of the meshing force $F_{m2}$ of the low-speed stage, though with smaller amplitudes. This frequency domain behavior reveals that the coupling effect between the meshing vibrations of different gear pairs is asymmetric.

This phenomenon occurs because the torsional internal force of the connecting shaft couples the vibration displacements of different frequencies together, which then act on the two connected components separately as force and reaction. The coupled components, in turn, feed back the vibration displacement containing new frequencies to the meshing force of the gear pair in the form of equivalent meshing line deformation. As a result, mutual coupling arises between the meshing forces of different gear pairs.

Fig. 2Dynamic meshing force of gear pair

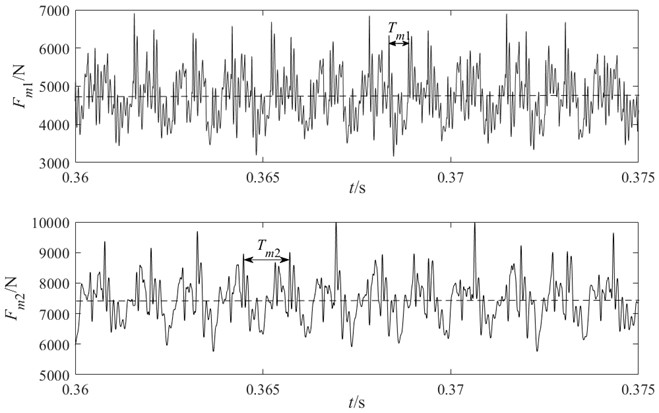
Fig. 3Spectrum of meshing forces

5.2. Characteristics of dynamic load coefficient

The dynamic characteristics of the gear system, particularly under high-speed operating conditions, have a direct impact on its overall performance. In this study, the dynamic load coefficient is used as an indicator to evaluate the dynamic behavior of the gear transmission system. The dynamic load coefficient $G_m\left(t\right)$ is defined as:

28

$G_m\left(t\right)=\max \left(\frac{F_m\left(t\right)}{F_m^{\text{'}}}\right),$

where, $F_m\left(t\right)$ denotes the dynamic meshing force, and $F_m^{\text{'}}$ represents the static meshing force.

The relationship between the dynamic load coefficient and the meshing frequency is shown in Fig. 4. It can be observed that, within the investigated frequency range, the dynamic load coefficient of gear pair $m_1$ is significantly higher than that of gear pair $m_2$. This is attributed to the higher rotational speed and more pronounced vibration of gear pair $m_1$. Furthermore, when the meshing frequency approaches the natural frequency of the system, both dynamic load coefficients $G_{m1}$ and $G_{m2}$ exhibit a sharp increase, which is caused by the strong primary resonance response of the system.

Fig. 4Dynamic load coefficients of the system

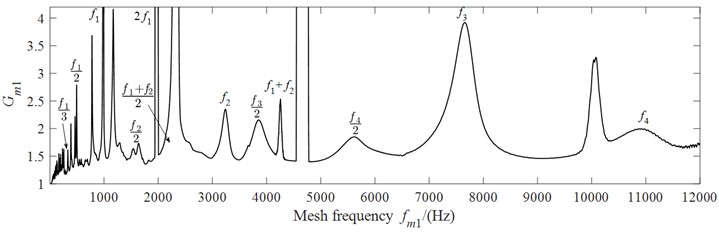
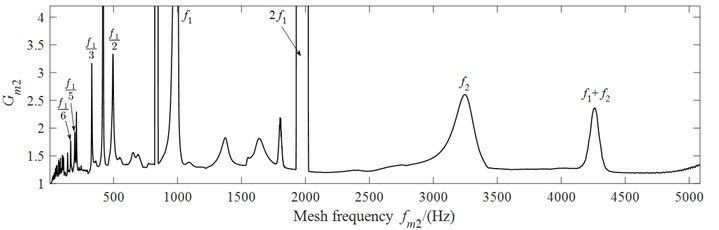
Owing to the time-varying meshing stiffness of the gears, parametric vibrations are excited. The meshing frequencies $f_{m1}$ and $f_{m2}$ induce subharmonic resonance, superharmonic resonance, and additive combination resonance responses in the system.

Specifically, when integer multiples of the meshing frequency (e.g., $2f_{m1}$ or $3f_{m1}$) approach the natural frequencies $f_1$ or $f_2$, superharmonic resonance is observed, resulting in a distinct resonance peak. Similarly, subharmonic resonance occurs when $f_{m1}=2f_1$ or $f_{m2}=2f_1$, which is accompanied by a broader resonance region in the vicinity.

When the meshing frequency or one of its harmonics approaches the sum of two natural frequencies, a pronounced additive combination resonance occurs, accompanied by a distinct peak in the dynamic load coefficient. Specifically, resonances at $f_{m1}=f_1+f_2$ and $f_{m2}=f_1+f_2$ are directly excited by the fundamental meshing frequency, whereas resonance at $f_{m1}=\frac{\left(f_1+f_2\right)}{2}$ is driven by the second harmonic of the meshing frequency.

The time-varying meshing stiffness in multistage gear transmission systems induces parametric excitation and dynamic coupling between different gear pairs, leading to complex resonance phenomena. Effectively addressing these issues requires a systematic and multi-faceted approach focused on shifting critical resonance frequencies outside the operational range, reducing vibration amplitudes, or mitigating their dynamic impact.

By adjusting the stiffness or rotational inertia of relevant components – for example, by modifying the diameter of the intermediate shaft or optimizing the bearing span – the natural frequencies of the system can be effectively adjusted. In addition, through rational design of gear transmission ratios and operating speeds, it can be ensured that all meshing frequencies, along with their harmonics and subharmonics, avoid coincidence with the system’s natural frequencies or their combination frequencies.

The use of high-contact-ratio (HCR) gears contributes to reducing the fluctuation amplitude of mesh stiffness, thereby mitigating parametric excitation effects. Furthermore, increasing system damping can effectively suppress resonance peak amplitudes. The installation of torsional vibration isolators on intermediate shafts can decouple the transmission of vibrational energy along the drive train.

6. Conclusions

This study established a nonlinear torsional dynamic model for an integrated electric drive system comprising a PMSM and a two-stage gear train. Using the multi-scale method and numerical simulations, the parametric instability and vibration characteristics induced by time-varying mesh stiffness were thoroughly investigated. The principal conclusions are as follows:

1) In the time domain, the dynamic meshing force oscillates around the static meshing force value, accompanied by high-frequency, small-amplitude fluctuations.

2) The frequency spectrum of the meshing force contains not only the meshing frequency of the current gear pair, but also the natural frequencies of the system and the meshing frequencies of other gear pairs.

3) Within the frequency range studied, the dynamic load coefficient of high-speed gear pair $m_1$ is significantly greater than that of the low-speed gear pair $m_2$.

4) The dynamic load coefficient of the gear pair peaks not only under the primary resonance conditions, but also during subharmonic, superharmonic, and combination resonance responses. In particular, when the meshing frequency approaches twice the first-order natural frequency, the instability regions induced by subharmonic resonance is significantly larger.

The analytical approach developed in this work can be extended and applied to more complex integrated electric drive systems than those considered here, such as systems incorporating permanent magnet synchronous motors coupled with planetary gear transmission mechanisms.