Modeling the operation of an eccentric-pendulum resonant vibration stand for testing aviation industry products

Svyshch, Taras; Lanets, Oleksii; Maistruk, Pavlo; Derevenko, Iryna; Nazar, Ihor; Khomych, Ivan

doi:10.21595/vp.2025.25064

Vibroengineering Procedia

Browse Procedia

Published: September 30, 2025

Check for updates

Modeling the operation of an eccentric-pendulum resonant vibration stand for testing aviation industry products

Taras Svyshch¹

Oleksii Lanets²

Pavlo Maistruk³

Iryna Derevenko⁴

Ihor Nazar⁵

Ivan Khomych⁶

¹Department of Design Machine and Automotive Engineering, Lviv Polytechnic National University, Lviv, Ukraine

^{2, 5, 6}Department of Aviation and Manufacturing Engineering, Lviv Polytechnic National University, Lviv, Ukraine

³Department of Robotics and Integrated Mechanical Engineering Technologies, Lviv Polytechnic National University, Lviv, Ukraine

⁴Department of Strength of Materials and Structural Mechanics, Lviv Polytechnic National University, Lviv, Ukraine

Corresponding Author:

Pavlo Maistruk

Cite the article Download PDF

Downloads 74

Abstract

The article presents a mathematical model of the oscillation system of a resonant vibration stand with an eccentric-pendulum drive. The principle of operation of this stand is as follows. A shaft is installed in the body of the reactive body, on which a pendulum is placed with eccentricity. The shaft is driven by an asynchronous electric motor through a flexible coupling. The pendulum and the reactive body are periodically displaced relative to each other by the amount of eccentricity due to the rotation of the shaft. The working (active) body is disturbed by the movement of the reactive body. The article outlines the advantages of machines of this type in comparison with the most common types. A mathematical model is compiled in the form of seven second-order differential equations. The parameters of the mechanical oscillation system and drive are given. The operation of the oscillation system of the resonant vibration stand is simulated. As a result of mathematical modeling, it was established that this model of the vibration stand is promising for implementation in industry.

Modeling the operation of an eccentric-pendulum resonant vibration stand for testing aviation industry products

Highlights

The developed and analyzed mathematical model of the eccentric-pendulum type vibrating table in transient and steady-state operating modes indicates that the design is operational. Analysis of the motion of the oscillating masses confirms the correctness of the parameters set.
Thanks to the use of a pendulum, it is possible to minimize the amplitudes of vibrations of the vibration stand in the horizontal direction.
The implementation of a working body driven by a kinematically perturbed reactive body enabled a 2.5-fold increase in the vertical vibration amplitudes compared to the previous design.

1. Introduction

Specialized stands are widely used for vibration testing of aviation industry products. Such vibration stands are used to establish the natural frequencies of the structure under study or for long-term vibration resistance testing. The first type of stands provides a wide range of changes in the frequency of forced oscillations [1], the second type mainly operates at a clearly established frequency. The object of study of this article is the second type of vibration stands, operating at a clearly established frequency of forced oscillations. Such stands have much in common with vibration technological equipment.

Resonant designs of vibration tables (stands) are known, which provide amplification of vibrations in the vertical direction, but do not prevent lateral and angular perturbation of the working body [2]. To prevent this, two vibrator motors are used in industry, rotating towards each other [3]-[5]. More complex inertial drive designs are also used [6], [7]. But this further complicates the two-mass design. It is more expedient to implement a structurally simpler resonant vibrating table with an unbalanced drive [5]. It uses paired vibrator motors, the vibration exciters of which rotate towards each other, allowing only the vertical component of the disturbance. However, in such a design, a change in the load mass and a change in its location on the surface of the vibrating table can cause undesirable transient processes, during which lateral and angular vibrations will occur due to a violation of the self-synchronization of the two vibration exciters.

Vibration machines with an electromagnetic drive are also used as technological equipment. However, the highly efficient designs [8], [9] of such vibration machines have a number of disadvantages, in particular those related to the stability of functioning in the interresonant oscillation mode.

There are vibration drives with an eccentric-pendulum drive [10] and crank-type exciters [11, 12]. Such machines are partially devoid of the disadvantages of vibration machines with an unbalanced drive. They reach the nominal operating modes from a state of rest in a short period of time and rapidly stop. Structurally, the vertical directional movement of the working body is simply implemented. Working near such vibrating equipment is much safer. However, such equipment is non-resonant.

The authors of the article will demonstrate an attempt to implement a model of a resonant vibration stand using an eccentric-pendulum drive. It is assumed to use only one electric motor and the absence of mechanisms for forced direction of oscillations.

2. Description of the schematic diagram and dynamic model of a resonant vibration stand with an eccentric-pendulum drive

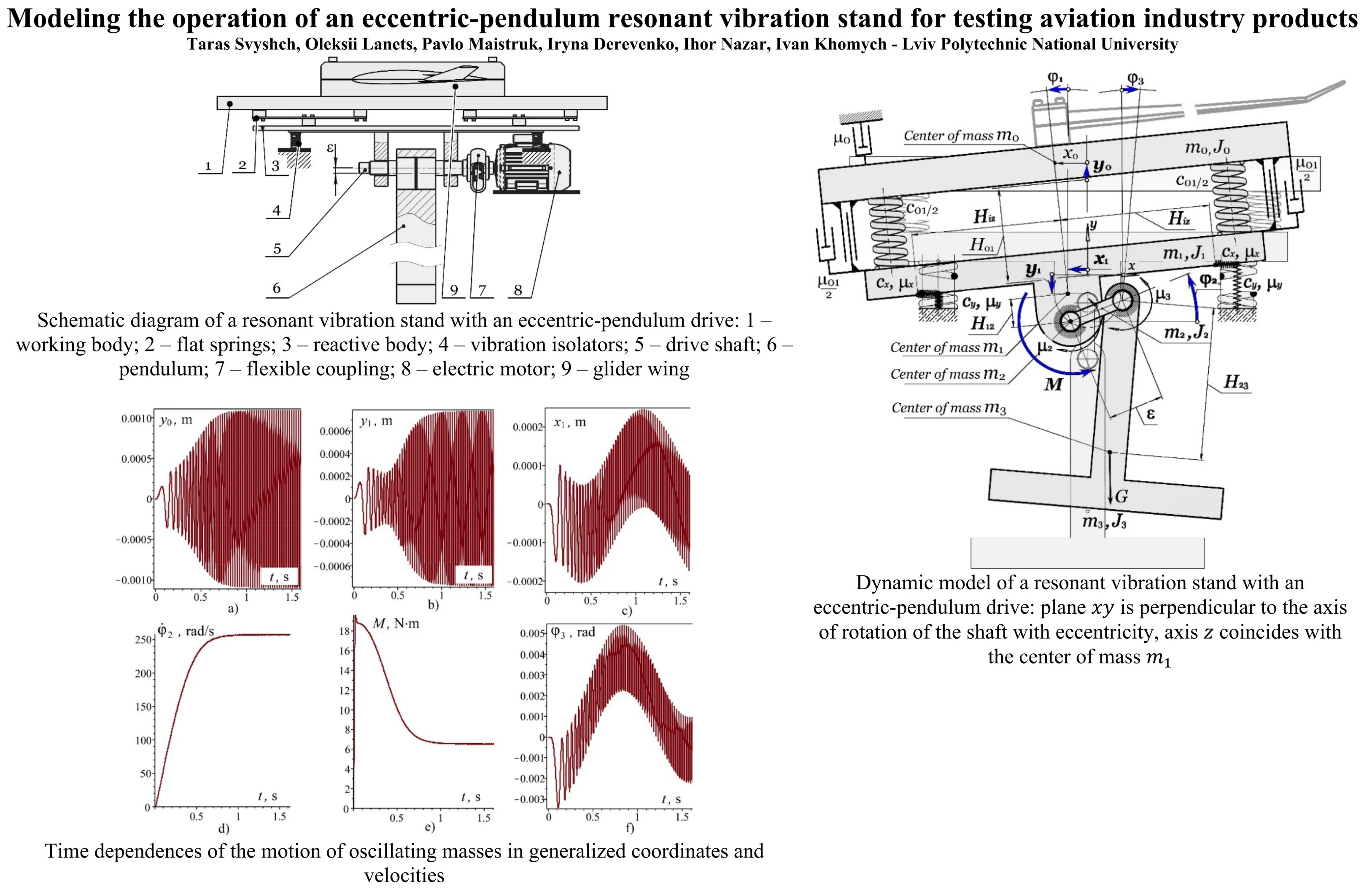
Fig. 1 shows a schematic diagram of the proposed eccentric-pendulum type vibration stand. The working body 1 is connected to the reactive body 3 through resonant elastic elements 2, which are mounted on the foundation through vibration isolators 4 (elements with a low stiffness coefficient in the vertical direction). The drive shaft 5 is installed in the housing of the reactive body 3, on which the pendulum 6 is mounted with eccentricity $ε$ . The shaft 5 is driven by an asynchronous electric motor 8 through a flexible coupling 7. The pendulum 6 and the reactive body 3 are periodically displaced relative to each other by an amount $ε$ due to the rotation of the shaft 5. The working (active) body 1 is disturbed by the movement of the reactive body 3. The glider wing 9 is rigidly cantilevered to the working body. This stand is being developed precisely to study the vibration resistance of the glider wing.

Fig. 1Schematic diagram of a resonant vibration stand with an eccentric-pendulum drive: 1 – working body; 2 – flat springs; 3 – reactive body; 4 – vibration isolators; 5 – drive shaft; 6 – pendulum; 7 – flexible coupling; 8 – electric motor; 9 – glider wing

Schematic diagram of a resonant vibration stand with an eccentric-pendulum drive: 1 – working body; 2 – flat springs; 3 – reactive body; 4 – vibration isolators; 5 – drive shaft; 6 – pendulum; 7 – flexible coupling; 8 – electric motor; 9 – glider wing

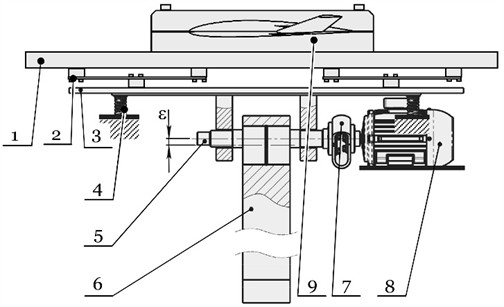
Consider a flat model of a vibration stand (Fig. 2). Establish a basic coordinate system $x y z$ , the plane $x y$ of which is perpendicular to the axis of rotation of the shaft with eccentricity, and the axis $y$ is directed vertically. The axis $z$ coincides with the center of mass $m_{1}$ . The oscillatory system consists of four absolutely rigid bodies: a working body with a mass $m_{0}$ (taking into account the load) with a moment of inertia $J_{0}$ about the axis passing through its center of mass perpendicular to the plane; $x y$ a reactive body with a mass $m_{1}$ with a moment of inertia $J_{1}$ ; an eccentric shaft with a mass $m_{2}$ with a moment of inertia about the axis of rotation $J_{2}$ and a pendulum with a mass $m_{3}$ with a moment of inertia $J_{3}$ about the axis passing through its center of mass perpendicular to the plane $x y$ . The parameter $J_{2}$ takes into account the moment of inertia of the rotor of the electric motor, in contrast to the parameter $m_{2}$ , which does not take into account the mass of the rotor. This is related to the fact that, due to the use of a lobe clutch, a mechanical decoupling is established between the shaft and the electric motor along the axes $x$ and $y$ . According to this, the oscillatory motion of the reactive body has practically no effect on the rotor of the electric motor. The working body $m_{0}$ is connected by mass to the reactive body by mass $m_{1}$ through resonant elastic elements with stiffness coefficient $c_{01}$ along the axis $y$ . It is assumed that the mass $m_{0}$ rotates together with the mass $m_{1}$ .

Fig. 2Dynamic model of a resonant vibration stand with an eccentric-pendulum drive: plane xy is perpendicular to the axis of rotation of the shaft with eccentricity, axis z coincides with the center of mass m1

Dynamic model of a resonant vibration stand with an eccentric-pendulum drive: plane xy is perpendicular to the axis of rotation of the shaft with eccentricity, axis z coincides with the center of mass m1

The motion of the system can be described using the following independent coordinates: oscillation of the mass $m_{0}$ along the axis $y$ by the generalized coordinate $y_{0}$ ; oscillation of the mass $m_{1}$ along the axes $x$ , $y$ and around its own center of mass in the plane $x y$ by the generalized coordinates $x_{1}$ , $y_{1}$ and $φ_{1}$ ; rotational motion of the masses $m_{2}$ and $m_{3}$ around their own centers of mass in the plane $x y$ by the generalized coordinates $φ_{2}$ and $φ_{3}$ . Furthermore, we additionally consider the moment of disturbance $M$ of the electric motor as a generalized coordinate. Therefore, the oscillatory system has seven degrees of freedom.

The distance from the center of mass $m_{0}$ to the center of mass $m_{1}$ is denoted by $H_{01}$ . The distance from the center of mass $m_{1}$ to the shaft axis is denoted by $H_{12}$ , and from the shaft to the center of mass $m_{3}$ – $H_{23}$ . The horizontal distance from the vibration isolators to the center of mass of the reactive body is denoted by $H_{i z}$ . The vibration system is mounted on a fixed base through vibration isolators attached from below to the reactive body, and their stiffness coefficients along the axes $x$ and $y$ are respectively $c_{x}$ and $c_{y}$ . To take into account the effect of the load on the working body, the viscous resistance coefficient is introduced $μ_{0}$ . The coefficients $μ_{x}$ and $μ_{y}$ determine the energy dissipation in the vibration isolators during the movement of the mass $m_{1}$ along the axes, respectively, $x$ and $y$ . The coefficient $μ_{2}$ reflects the viscous friction in the bearings between the reactive body and the shaft (between the masses $m_{1}$ and $m_{2}$ ), and $μ_{3}$ between the shaft and the pendulum (between the masses $m_{2}$ and $m_{3}$ ). The dynamic effect of the cantilevered wing on the working body is not considered in this study.

The linear and angular coordinates for each of the masses $m_{0}$ , $m_{1}$ , $m_{2}$ and $m_{3}$ can be written as follows. By deviating the center of mass from the equilibrium position $m_{1}$ , its generalized coordinates along the axes $x$ and $y$ are written as $(- x_{1})$ and $(- y_{1})$ (Fig. 2). The working body (mass $m_{0}$ ) moves along the axis $y$ along the generalized coordinate $y_{0}$ . The angular deviation of the mass $m_{0}$ and mass $m_{1}$ from its own center of mass is determined by the angular coordinate $φ_{1}$ . The angular deviations of the masses $m_{2}$ and $m_{3}$ around their own centers of mass are determined by the angular coordinates respectively $φ_{2}$ and $(- φ_{3})$ .

The remaining linear coordinates of the centers of mass $m_{0}$ , $m_{2}$ and $m_{3}$ are dependent and are determined through generalized coordinates as follows: $x_{0} = - x_{1} - H_{02} \sin φ_{1};$ $x_{2} = - x_{1} + H_{12} \sin φ_{1};$ $x_{3} = - x_{1} + H_{12} \sin φ_{1} + ε \cos φ_{2} - H_{23} \sin φ_{3};$ $y_{2} = - y_{1} - H_{12} \cos φ_{1}$ ; $y_{3} = - y_{1} - H_{12} \cos φ_{1} + ε \sin φ_{2} - H_{23} \cos φ_{3}$ .

Therefore, there are 12 coordinates that completely describe the motion of the four oscillating masses in the plane. Since the angular oscillations of the jet body (mass $m_{1}$ ) and the pendulum (mass $m_{3}$ ) around their own centers of mass are small, to simplify further calculations we will use the following approximations: $\sin φ_{1,3} \approx φ_{1,3}$ , $\cos φ_{1,3} \approx 1$ , which are valid for small values of $φ_{1,3}$ . The system of differential equations of motion of oscillating masses in seven generalized coordinates is formed using generalized Lagrange equations of the second-order. Taking into account the equation of an asynchronous electric motor [13] the system of equations has the form:

1

(m_{0} + m_{1} + m_{2} + m_{3}) {\ddot{x}}_{1} + [m_{0} H_{01} - (m_{2} + m_{3}) H_{12}] {\ddot{φ}}_{1} + m_{3} [ε ({\dot{φ}}_{2}^{2} \cos φ_{2} + {\ddot{φ}}_{2} \sin φ_{2}) + H_{23} {\ddot{φ}}_{3}] + c_{x} x_{1} + μ_{x} {\dot{x}}_{1} = 0,

m_{0} {\ddot{y}}_{0} + с_{01} (y_{0} - y_{1}) + μ_{01} ({\dot{y}}_{0} - {\dot{y}}_{1}) + μ_{0} {\dot{y}}_{0} = 0,

(m_{1} + m_{2} + m_{3}) {\ddot{y}}_{1} + m_{3} ε ({\dot{φ}}_{2}^{2} \sin φ_{2} + {\ddot{φ}}_{2} \cos φ_{2}) + с_{01} (y_{1} - y_{0}) + c_{y} y_{1} + μ_{01} ({\dot{y}}_{1} - {\dot{y}}_{0}) + μ_{y} {\dot{y}}_{1} = 0,

(J_{0} + J_{1} + (m_{2} + m_{3}) H_{12}^{2} + m_{0} H_{01}^{2}) {\ddot{φ}}_{1} - (H_{01} m_{0} - (m_{2} + m_{3}) H_{12}) {\ddot{x}}_{1} - m_{3} H_{12} (ε ({\dot{φ}}_{2}^{2} \cos φ_{2} + {\ddot{φ}}_{2} \sin φ_{2}) - H_{23} {\ddot{φ}}_{3}) + c_{y} H_{і z}^{2} φ_{1} + μ_{y} H_{і z}^{2} {\dot{φ}}_{1} + μ_{2} ({\dot{φ}}_{1} - {\dot{φ}}_{2}) = - m_{3} g H_{12} \sin φ_{1} - m_{3} g ε \cos φ_{2} \cos φ_{3},

(J_{2} + m_{3} ε^{2}) {\ddot{φ}}_{2} + m_{3} ε ({\ddot{x}}_{1} \sin φ_{2} - {\ddot{y}}_{1} \cos φ_{2} - H_{12} {\ddot{φ}}_{1} \sin φ_{2} + H_{23} {\ddot{φ}}_{3} \sin φ_{2}) + μ_{2} ({\dot{φ}}_{2} - {\dot{φ}}_{1}) + μ_{3} ({\dot{φ}}_{2} - {\dot{φ}}_{3}) = M - m_{3} g ε \cos φ_{2} \cos φ_{3},

(J_{3} + m_{3} H_{23}^{2}) {\ddot{φ}}_{3} + m_{3} H_{23} ({\ddot{x}}_{1} - H_{12} {\ddot{φ}}_{1}) + m_{3} H_{23} ε ({\dot{φ}}_{2}^{2} \cos φ_{2} + {\ddot{φ}}_{2} \sin φ_{2}) + μ_{3} ({\dot{φ}}_{3} - {\dot{φ}}_{2}) = - m_{3} g H_{23} \sin φ_{3},

- \frac{2 M_{m a x} (ω_{0} - {\dot{φ}}_{2})}{(1 + \frac{(ω_{0} - {\dot{φ}}_{2})^{2}}{{ω_{0}}^{2}}) ω_{0}} + \frac{T_{D} \ddot{M}}{1 + \frac{(ω_{0} - {\dot{φ}}_{2})^{2}}{{ω_{0}}^{2}}} + \frac{T_{D} (2 + \frac{T_{D} {\ddot{φ}}_{2}}{ω_{0} - {\dot{φ}}_{2}}) \dot{M}}{1 + \frac{(ω_{0} - {\dot{φ}}_{2})^{2}}{{ω_{0}}^{2}}} + (1 + \frac{T_{D} {\ddot{φ}}_{2}}{(1 + \frac{(ω_{0} - {\dot{φ}}_{2})^{2}}{{ω_{0}}^{2}}) (ω_{0} - {\dot{φ}}_{2})}) M = 0 .

The values of the parameters of the oscillatory system included in the developed mathematical model are as follows: $c_{x} = 17500$ N/m; $c_{y} = 22500$ N/m; $ε = 0.001$ m; $g = 9.8$ m/s²; $H_{01} = 0.225$ m; $H_{12} = 0.125$ m; $H_{23} = 0.225$ m; $H_{i z} = 0.32$ m; $I_{0} = 13.5$ kg∙m²; $J_{1} = 8$ kg∙m²; $I_{2} = 0.03$ kg∙m²; $J_{3} = 7.8$ kg∙m²; $m_{0} = 200$ kg; $m_{1} = 110$ kg; $m_{2} = 20$ kg; $m_{3} = 154$ kg; $μ_{x} = μ_{y} = μ_{01} = 5000$ N∙m/s; $μ_{0} = 10000$ N∙m/s; $μ_{2} = 0.007$ N∙m∙s/rad; $μ_{3} = 0.0035$ N∙m∙s/rad. In addition, the maximum torque in the electric motor is $M_{m a x}$ = 18.7 N∙m; the electromagnetic time constant of the electric motor $T_{D} =$ 0.074; the synchronous angular speed of rotation of the rotor of the electric motor is $ω_{0} = 314$ rad/s. The model of the electric motor – 4A90L2Y3, with the power of 3 kW.

3. Results of mathematical modeling of the operation of a vibration stand with an eccentric-pendulum drive

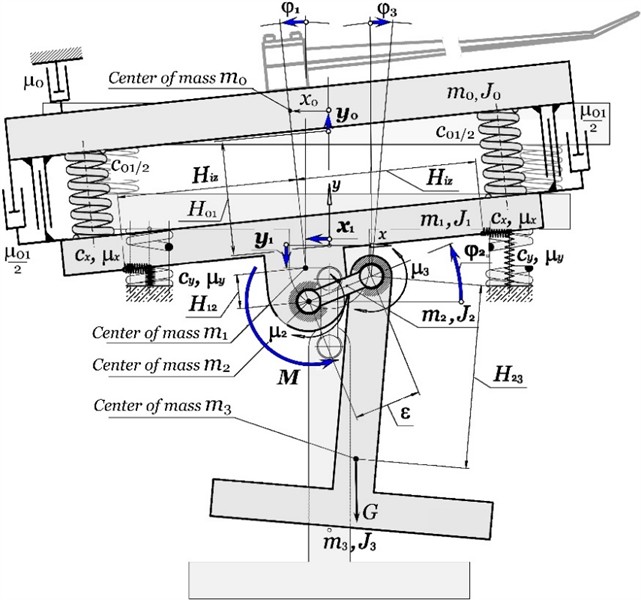
The above data are sufficient to solve the system numerically. The system Eq. (1) was solved using the Rosenbrock numerical method in the Maple software. The initial conditions for the values of the generalized coordinates and their velocities are equal to zero. Of greatest interest are the transient modes of operation of the vibration stand. For this purpose, the time is limited to the first 1,5 seconds. The obtained dependences of the system motion on generalized coordinates and velocities are shown in Fig. 3.

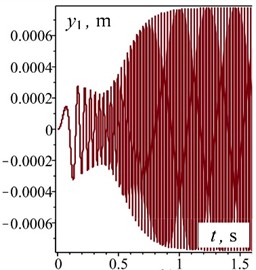
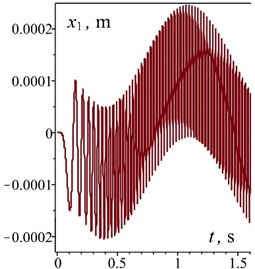
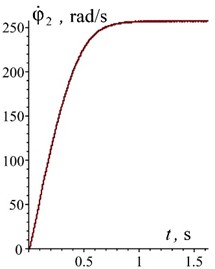
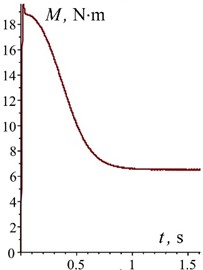
Fig. 3Time dependences of the motion of oscillating masses in generalized coordinates and velocities

a)

b)

c)

d)

e)

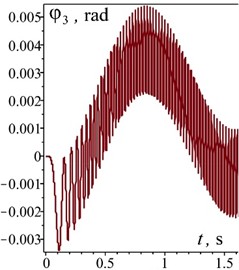
f)

The obtained dependences indicate that the oscillatory system reaches a steady state (the electric motor reaches its rated speed) in approximately 1 s without significant dynamic overloads. This is clearly seen in the characteristics of the disturbing moment in the electric motor (Fig. 3(e)), the characteristics of the rotor speed of the electric motor (Fig. 3(d)), and the characteristics of the oscillatory motion of the reactive body (Fig. 3(b)). The established oscillations of the working body along the vertical axis are $Y_{0} =$ 1.1 mm (Fig. 3(a)) at the angular velocity of the rotor of the electric motor ${\dot{φ}}_{2} = Ω =$ 260 rad/s (Fig. 3(d)). In this case, the overload on the working body is $ξ = Y_{0} Ω^{2} / g =$ 7.6. This meets the necessary technical requirements for the vibration stand. The oscillations of the reactive body along the horizontal axis at the frequency of forced oscillations are $x_{1} =$ 0.11 mm (Fig. 3(c)). The horizontal amplitude of oscillations for the working body is practically the same. The pendulum performs oscillatory motion around the shaft axis with a period of 1.5 s (Fig. 3(f)).

4. Conclusions

The developed and analyzed mathematical model of the eccentric-pendulum type vibrating table in transient and steady-state operating modes indicates that the design is operational. Analysis of the motion of the oscillating masses confirms the correctness of the parameters set.

Thanks to the use of a pendulum, it is possible to minimize the amplitudes of vibrations of the vibration stand in the horizontal direction. Thanks to the use of a working body, which is driven by a reactive body (kinematically perturbed), it was possible to increase the amplitudes of mass vibrations in the vertical direction by 2.5 times compared to the design [10].

References

M. Böswald and Y. Govers, “Taxi vibration testing – an alternative method to ground vibration testing of large aircraft,” in International Conference on Noise and Vibration Engineering, pp. 2413–2426, 2008.

Search CrossRef
N. Yaroshevich, O. Yaroshevych, and V. Lyshuk, “Drive dynamics of vibratory machines with inertia excitation,” in Mechanisms and Machine Science, Cham: Springer International Publishing, 2021, pp. 37–47, https://doi.org/10.1007/978-3-030-60694-7_2

Publisher
Z. V. Despotovic, A. M. Pavlovic, and D. Ivanic, “Exciting force frequency control of unbalanced vibratory actuators,” in 20th International Symposium on Power Electronics (Ee), pp. 1–6, Oct. 2019, https://doi.org/10.1109/pee.2019.8923574

Publisher
G. Cieplok and K. Wójcik, “Conditions for self-synchronization of inertial vibrators of vibratory conveyors in general motion,” Journal of Theoretical and Applied Mechanics, Vol. 58, No. 2, pp. 513–524, Apr. 2020, https://doi.org/10.15632/jtam-pl/119023

Publisher
O. Lanets, Fundamentals of Analysis and Design of Vibratory Machines. (in Ukrainian), Lviv, Ukraine: Lviv Polytechnic Publishing House, 2018.

Search CrossRef
V. Gursky, P. Krot, V. Korendiy, and R. Zimroz, “Dynamic analysis of an enhanced multi-frequency inertial exciter for industrial vibrating machines,” Machines, Vol. 10, No. 2, p. 130, Feb. 2022, https://doi.org/10.3390/machines10020130

Publisher
V. Gursky, I. Kuzio, P. Krot, and R. Zimroz, “Energy-saving inertial drive for dual-frequency excitation of vibrating machines,” Energies, Vol. 14, No. 1, p. 71, Dec. 2020, https://doi.org/10.3390/en14010071

Publisher
P. Maistruk, O. Lanets, V. Maistruk, and I. Derevenko, “Establishment of the natural frequency of oscillations of the two-dimensional continuous member of the vibrating table,” Journal of Theoretical and Applied Mechanics, Vol. 52, No. 3, pp. 199–214, Aug. 2022, https://doi.org/10.55787/jtams.22.52.3.199

Publisher
P. Maistruk, O. Lanets, and V. Maistruk, “Determining the influence of continuous section shape and dimensions on stresses over a wide range of vibration frequency,” Ukrainian Journal of Mechanical Engineering and Materials Science, Vol. 10, No. 4, pp. 54–69, Jan. 2024, https://doi.org/10.23939/ujmems2024.04.054

Publisher
O. S. Lanets, V. T. Dmytriv, V. M. Borovets, I. A. Derevenko, and I. M. Horodetskyy, “Analytical model of the two-mass above resonance system of the eccentric-pendulum type vibration table,” International Journal of Applied Mechanics and Engineering, Vol. 25, No. 4, pp. 116–129, Dec. 2020, https://doi.org/10.2478/ijame-2020-0053

Publisher
V. Korendiy, O. Lanets, O. Kachur, P. Dmyterko, and R. Kachmar, “Determination of inertia-stiffness parameters and motion modelling of three-mass vibratory system with crank excitation mechanism,” Vibroengineering Procedia, Vol. 36, pp. 7–12, Mar. 2021, https://doi.org/10.21595/vp.2021.21924

Publisher
O. Kachur and V. Korendiy, “Dynamic behavior of vibratory screening conveyor equipped with crank-type exciter,” in Lecture Notes in Mechanical Engineering, Cham: Springer Nature Switzerland, 2023, pp. 44–53, https://doi.org/10.1007/978-3-031-32774-2_5

Publisher
W. Wenske, “On the derivation of the dynamic characteristic of the asynchronous motor with regard to the calculation of vibration phenomena in propulsion systems,” (in German), Scientific Journal of the O. Guericke University of Technology, Vol. 14, No. 5/6, pp. 517–523, 1970.

Search CrossRef

About this article

Received

May 13, 2025

Accepted

July 14, 2025

Published

September 30, 2025

SUBJECTS

Mechanical vibrations and applications

DOI

https://doi.org/10.21595/vp.2025.25064

Keywords

harmonic vibrations

oscillating system

mathematical model

differential equations

time dependences

electric motor

Acknowledgements

The authors have not disclosed any funding.

Data Availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Conflict of interest

The authors declare that they have no conflict of interest.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2021 12 02

Mathematical modeling of forced oscillations of semidefinite vibro-impact system sliding along rough horizontal surface

Vitaliy Korendiy, Volodymyr Gursky, Oleksandr Kachur, Volodymyr Gurey, Oleksandr Havrylchenko, Oleh Kotsiumbas

Research article

2017 11 15

The dynamics of eccentric vibration mechanism (Part 1)

A. Leonid Igumnov, S. Vladimir Metrikin, V. Irina Nikiforova

Research article

2014 08 15

Theoretical study on self-synchronization of two homodromy rotors coupled with a pendulum rod in a far-resonant vibrating system

Pan Fang, Qiming Yang, Yongjun Hou, Ye Chen

T. Svyshch, O. Lanets, P. Maistruk, I. Derevenko, I. Nazar, and I. Khomych, “Modeling the operation of an eccentric-pendulum resonant vibration stand for testing aviation industry products,” Vibroengineering Procedia, Vol. 59, pp. 34–40, Sep. 2025, https://doi.org/10.21595/vp.2025.25064

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2025.25064
UR  - https://doi.org/10.21595/vp.2025.25064
TI  - Modeling the operation of an eccentric-pendulum resonant vibration stand for testing aviation industry products
T2  - Vibroengineering Procedia
AU  - Svyshch, Taras
AU  - Lanets, Oleksii
AU  - Maistruk, Pavlo
AU  - Derevenko, Iryna
AU  - Nazar, Ihor
AU  - Khomych, Ivan
PY  - 2025
DA  - 2025/09/30
PB  - Extrica
SP  - 34-40
VL  - 59
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

 @article{Svyshch_2025, title={Modeling the operation of an eccentric-pendulum resonant vibration stand for testing aviation industry products}, volume={59}, ISSN={2538-8479}, url={https://doi.org/10.21595/vp.2025.25064}, DOI={10.21595/vp.2025.25064}, journal={Vibroengineering Procedia}, publisher={JVE International Ltd.}, author={Svyshch, Taras and Lanets, Oleksii and Maistruk, Pavlo and Derevenko, Iryna and Nazar, Ihor and Khomych, Ivan}, year={2025}, month=sep, pages={34–40} }

Copy Bibtex

Copied to clipboard!

[1]T. Svyshch, O. Lanets, P. Maistruk, I. Derevenko, I. Nazar, and I. Khomych, “Modeling the operation of an eccentric-pendulum resonant vibration stand for testing aviation industry products,” Vibroengineering Procedia, vol. 59, pp. 34–40, Sep. 2025, doi: 10.21595/vp.2025.25064.

Copy IEEE

Copied to clipboard!

Svyshch, Taras, Oleksii Lanets, Pavlo Maistruk, Iryna Derevenko, Ihor Nazar, and Ivan Khomych. “Modeling the Operation of an Eccentric-Pendulum Resonant Vibration Stand for Testing Aviation Industry Products.” Vibroengineering Procedia 59 (September 30, 2025): 34–40. https://doi.org/10.21595/vp.2025.25064.

Copy Chicago

Copied to clipboard!

Modeling the operation of an eccentric-pendulum resonant vibration stand for testing aviation industry products

Abstract

Highlights

1. Introduction

2. Description of the schematic diagram and dynamic model of a resonant vibration stand with an eccentric-pendulum drive

3. Results of mathematical modeling of the operation of a vibration stand with an eccentric-pendulum drive

4. Conclusions

References

About this article

Related Articles