Establishing the natural frequency of oscillations of a continuous system with a concentrated mass in aviation and manufacturing engineering

1. Introduction

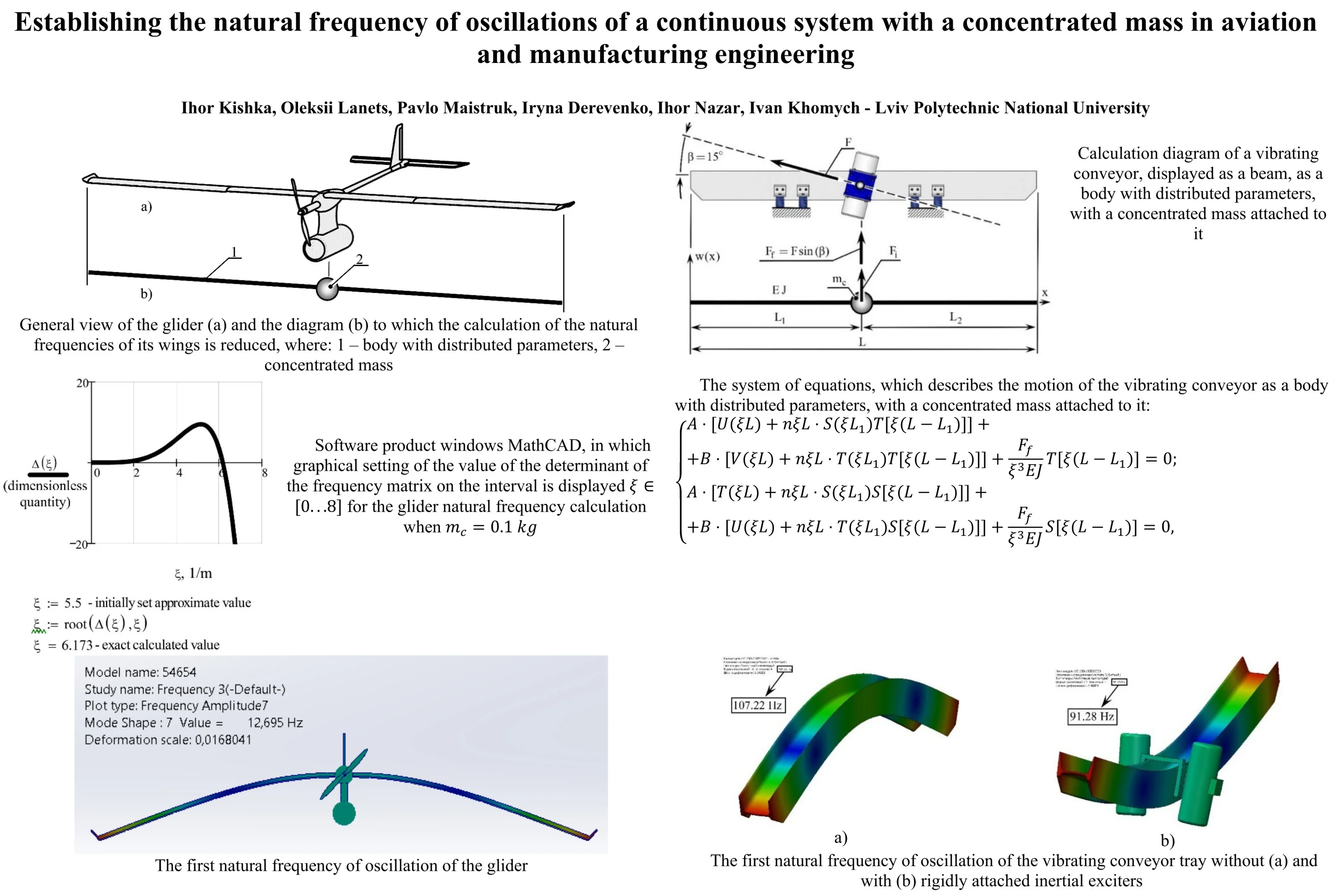
Absolutely solid bodies do not exist in nature. All of them are bodies with distributed parameters (continuous). Under dynamic loads of any body, its deformation and displacement of layers occur. This must be taken into account, especially when designing long products (wings of airplanes and gliders) that perceive pulsating air flows (Fig. 1(a)), or alternating dynamic loads (Fig. 1(b)), for example, working elements (trays) of vibrating conveyors (Fig. 2).

Fig. 1a) General view of the glider and b) the diagram to which the calculation of the natural frequencies of its wings is reduced, where: 1 – body with distributed parameters, 2 – concentrated mass

In the article, the authors will focus on the study of vibrations in technological equipment. Thus, for stable and uniform vibration transportation of products, it is necessary to ensure that the natural frequency of oscillations of the working body (tray, as a body with distributed mass) is at least several times higher than the forced one. Therefore, it is necessary that at the frequency of forced oscillations, the working body performs oscillating motion as a completely solid body, that is, it is sufficiently rigid and at the same time light, structurally simple, and cheap to manufacture. Failure to comply with such requirements may lead to the fact that the amplitudes of parasitic oscillations of working bodies may be commensurate with the technologically necessary forced ones. In this case, unstable transportation of products along the working body of the vibrating conveyor is observed.

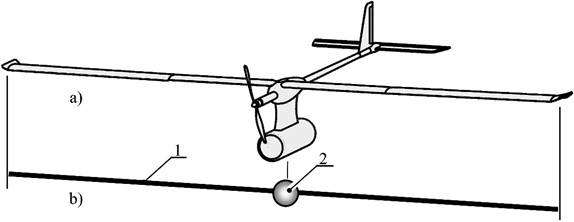
Considering one-mass vibratory conveyors, in which the inertial generator of oscillations is rigidly fixed on the working body (tray), it is appropriate to note that the incorporation of the inertial parameters of the drive to the natural frequency of oscillations of the tray is essential, since the masses of such actuators can be commensurate with the mass of the tray itself. This is especially noticeable in low-frequency oscillations.

Fig. 2Vibrating conveyor with an inertial exciters, where: 1 – working body (tray); 2 – inertial exciters (concentrated masses)

To date, the analytical methods of calculating mechanical oscillating systems are generally sufficiently described in educational literature [1], [2]. Many years of work by scientists have been included in the reference literature for engineers and scientists, for example [3]. Before proceeding to the objective review of works aimed at researching continuous systems [4], it is necessary to review the state of works on the design, modeling, and analysis of vibrating vehicles.

With the use of existing methods, engineers and scientists are engaged in the creation of new designs of vibrating technological equipment [5] and providing the necessary amplitude-frequency characteristics of oscillating systems [6].

However, in the above-mentioned works, no attention was paid to the study of the working bodies of conveyors or separators on their natural frequencies and shapes of oscillations. Ignoring the fact that the working body of vibrating technological equipment is not a completely solid body can lead to technological problems in the transportation or separation of products. These important issues were considered in work [7], and although the working bodies were considered as bodies with distributed parameters, concentrated masses, which in the models reflected the masses of inertial vibration exciters, were not taken into account. And if they were taken into account during the calculation using the finite element method, then a thorough analytical calculation was not carried out.

An analytical method for determining the natural frequencies of a system consisting of a homogeneous beam with a concentrated mass was developed in [8], but it was not possible to use it for this article. The solution of similar problems was carried out in works [9, 10], where continuous sections of vibrating technological equipment were thoroughly considered, and their frequency analysis was analytically carried out. However, the obtained mathematical models did not take into account concentrated masses. Currently, with the development of technologies, there is a tendency to abandon the classical analytical methods of calculating mechanical oscillatory systems. They were replaced by numerical methods that greatly simplify calculations, but underestimate the understanding of physical processes occurring during dynamic processes. Therefore, the main task of this article is to demonstrate an analytical approach in solving the applied problem of establishing the natural frequency of oscillations of the working body (tray) of a vibrating conveyor with an inertial vibration exciter, where the tray itself is considered as a body with distributed parameters containing a concentrated mass.

Based on the carried-out review of modern information sources dealing with modeling the dynamic behavior of discrete-continuous vibratory systems [9-12], it can be concluded that most of the existent investigations do not comprehensively take into account the simultaneous influence of the concentrated (discrete) masses and continuous elements while performing analytical solving of the corresponding problems. Therefore, this paper is focused on bridging the mentioned gap and analyzing the corresponding dynamic effects.

2. Mathematical model

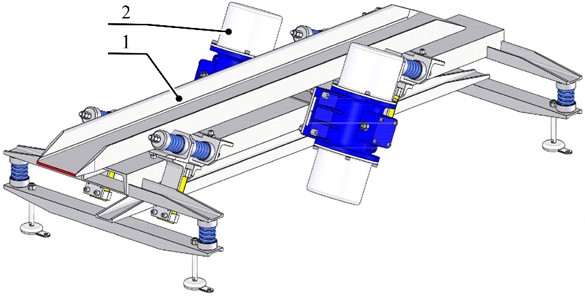
3D model of the vibrating conveyor, to the working body of which two inertial vibration exciters are rigidly attached, is shown in Fig. 3. A standard I-beam is used as a blank for the constructive implementation of the working body (tray). The vibrating conveyor rests on the foundation through eight vibration isolators made of coiled springs.

Fig. 33D model of a vibrating conveyor, where: 1 – working body (tray) made of I-beam; 2 – two inertial exciters; 3 – vibration isolators made of coiled springs

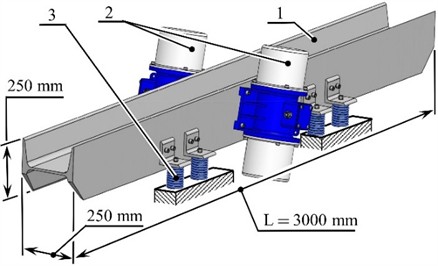
The object of research is a working body (a tray in the form of an I-beam), which is reduced to a homogeneous beam, considered to be a body with distributed parameters, with free ends and without supports along its length (Fig. 4). The total mass of two inertial vibration exciters is represented by the concentrated mass $m_c$. The influence of vibration isolators can be neglected. The beam performs transverse oscillations only in the plane $w$, $x$ – in the plane of action of the sign-changing total forced disturbance force caused by the action of inertial forces from two vibration exciters.

The beam is divided into two spans, the lengths of which are respectively $L_1$ and $L_2$, separated from each other by a concentrated mass $m_c$. On the length $L_1$ (on the left part of the beam), the deflection of the beam will be described by the function $w_l$, and on the length $L_2$ (on the right part of the beam) – by the function $w_r$. The influence of the concentrated mass on the beam’s natural vibration frequency and its shape will occur through two inertial parameters: the inertial force $F_i$ caused by its movement and the disturbance force $F_f$ caused by the force action of inertial exciters.

The system of equations, which describes the motion of the vibrating conveyor as a body with distributed parameters, with a concentrated mass attached to it, will take the form:

where $A,\mathrm{ }B\mathrm{ }$ – unknowns and:

are Krylov-Duncan functions; $\xi =\sqrt[4]{m_u{\omega }^2/EJ}$; $\omega$ – circular frequency of oscillations of the beam; $E$ – modulus of elasticity; $J$ – the moment of inertia of the cross-section of the beam relative to the neutral line of the cross-section, perpendicular to the bending plane; $EJ$ – bending stiffness of the cross section of the beam; $m_u$ – mass per unit of beam length.

Fig. 4Calculation diagram of a vibrating conveyor, displayed as a beam, as a body with distributed parameters, with a concentrated mass attached to it

3. Setting the natural frequency of a beam with a concentrated mass

Using the coefficients from Eq. (1) with unknowns $A$ and $B$, the frequency matrix, by which it is possible to set the natural frequency of oscillations of the beam taking into account the concentrated mass, will take the form:

where $n$ – concentrated mass ratio $m_c$ to the mass of the beam $m_{u}L$. The determinant of matrix Eq. (2) is

To establish the natural frequency of oscillations of the beam as a body with distributed parameters, on which the concentrated mass is located, previously set the necessary parameters $L_1=$1.5 m; $L_2=$1.5 m; $E=$2.1⋅10¹¹ Pa; $\rho =$ 7850 kg/m³. An I-beam was chosen as the tray of the vibrating conveyor SB 250×38×10.0 with the moment of inertia of the cross section $J=$3.26⋅10^-5·m⁴, and the mass of its unit length (meter) is $m_u=$ 85 kg. Inertial drives of Venanzetti Vibrazioni Milano company were considered. To ensure the necessary technological requirements, two inertial vibration exciters of the model were chosen as the drive VV41B/6, each of which power $N=$900 W and mass $m_1=$68 kg, total concentrated mass $m_c=$136 kg.

After equating to zero and finding the determinant Eq. (3), is formed a graphical dependence on the parameter $\xi$, which is shown in Fig. 5. The results represent the first non-zero root when $\mathrm{\Delta }\left(\xi \right)=0$. The first root symbolizes the first natural frequency of oscillations of the continuous system.

Using Eq. (2) and the value from Fig. 5, the first natural circular frequency of oscillations ${\omega }_1$ beams without and with a concentrated mass, respectively, will be:

Fig. 5Software product windows MathCAD, in which graphical setting of the value of the determinant Eq. (3) of the frequency matrix Eq. (2) on the interval is displayed ξ∈[0...2]

a)$m_c=$0 kg

b)$m_c=$136 kg

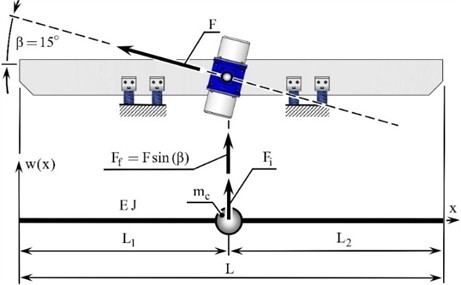
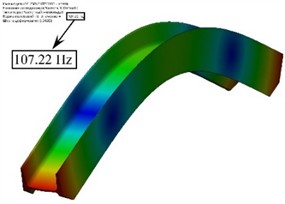
In order to check the analytical calculations, the first natural frequency of oscillations of the tray of the vibrating conveyor without and with rigidly attached inertial exciters was found using the finite element method in the SolidWorks software product (Fig. 6). The result almost completely coincides with the values obtained according to Eq. (4) and Eq. (5). The relative errors of analytical and numerical calculations are given in Table 1.

Considering the fact that the cyclic frequency of forced oscillations of the conveyor from the inertial vibration exciter is about $\nu =$16.6 Hz, it can be assumed that the oscillation amplitudes of parasitic oscillations will be minimal.

The natural frequency of a glider with concentrated mass is also considered. The main parameters of the glider are as follows: $L_1=$0.35 m; $L_2=$0.35 m; $E=$2.1⋅10⁹ Pa; $\rho =$1020 kg/m³. A wing with the moment of inertia of the cross section $J=$7⋅10^-10 m⁴, and the mass of its unit length (meter) is $m_u=$0.35 kg. Material of the glider – ABS plastic. After equating to zero and finding the determinant Eq. (3), a graphical dependence on the parameter $\xi$ is formed, which is shown in Fig. 7.

Fig. 6The first natural frequency of oscillation of the vibrating conveyor tray a) without and b) with rigidly attached inertial exciters

a)

b)

Fig. 7Software product windows MathCAD, in which graphical setting of the value of the determinant Eq. (3) of the frequency matrix Eq. (2) on the interval is displayed ξ∈[0...8] for the glider natural frequency calculation when mc= 0.1 kg

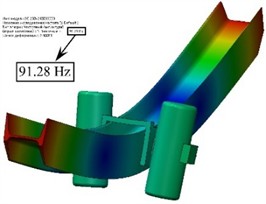
Fig. 8The first natural frequency of oscillation of the glider

The first natural circular frequency of oscillations ${\omega }_1$ of the glider with a concentrated mass will be:

As in the case of the conveyor, the first natural frequency of oscillations of the glider with concentrated mass was also found using the finite element method (Fig. 8). The result almost completely coincides with the values obtained according to Eq. (6).

Thus, the authors demonstrated the versatility of the proposed method for calculating the natural frequency of continuous bodies with concentrated masses in various industries.

4. Conclusions

During the setting of the natural frequency of oscillations of bodies with distributed parameters, as in our cases of the working body of a vibrating conveyor and glider, it is necessary to take into account the concentrated masses. Neglecting the concentrated mass when setting the natural frequency of the oscillating system leads to the fact that an overestimated value can be obtained (it is enough to analyze the results of calculations according to Eq. (4) and Eq. (5)). If the concentrated (discrete) mass is not properly considered, the continuous oscillatory system could reach the resonance working mode which is not recommended from the viewpoint of operability and performance. The reliability of analytical calculations was indirectly confirmed by numerical calculations using the finite element method in the SolidWorks software product.