Graphical analytical modeling of the kinematic scheme of a rock-piston pump

1. Introduction

In the technological processes of mortar pumps, for the best transportation of the mortar mixture, a crank-slider mechanism is used to drive the working element of a piston pump [1]. In the work [2], two variants of the kinematic diagram of a rotating yoke are presented; here, as a result of the synthesis of this mechanism, the optimal geometric parameters for both yoke mechanisms are given. In the kinematic studies [3], the use of a planetary mechanism for driving the working element of a mortar mixer is considered. Foreign researchers [4] are conducting work on combining two mechanisms: a crank-slider mechanism and a yoke mechanism for a pumping unit for pumping oil. Works [5, 6] are also being studied using a planetary mechanism for the working element of a pump for pumping viscous and heterogeneous liquids. The works [7, 8] present the results of scientific research on the operation of pumping equipment at drainage stations, in which an increase in vibration is observed due to hydro abrasive and cavitation wear of impellers, as well as destruction of seals, wear and increased temperature of bearings.

2. Research methodology

The research was conducted using the fundamental principles of the theory of mechanisms and machines, theoretical mechanics, and the fundamentals of construction machine design. The results of computer analysis of graphs and literary sources were used. The results were processed using mathematical statistics, and the paper was presented using computer graphics.

3. Results and discussion

Two types of kinematic schemes are investigated using a rocker-piston pump mechanism (Fig. 1(a)) for transporting mortar mixtures and a crank-piston pump (Fig. 1(b)). The mortar mixture is fed from receiving hopper 1 by vane devices, where it continuously mixes the mortar mass, to suction valve 2 of pump cylinder 4. When hopper valve 2 opens, the mortar mixture is discharged into the tank of pump hydraulic cylinder 4. After hydraulic cylinder 4 is filled with mortar, hopper valve 2 closes and conveyor valve 3 opens, and the mortar mixture is delivered to the consumer. Piston 5 is currently connected to rod 6, linkage 9 and linkage 10 (point $B$), and when linkage 10 moves from left to right, piston 5 (point $D$) moves from the left position to the right to point $D_1$: the working stroke occurs – phase ${\phi }_p$. In the operating mode of the pump, the solution mixture is squeezed into the conveyor under the pressure of piston 5, until the stop (point $D_1$) of the right position of piston 5. Before the reverse idle movement of piston 5, valve 3 of the conveyor closes, the link 10 from the right position (point $B_1$) moves to the left, dragging piston 5 and piston rod 6 (rod 6 - piston 5) along with it, valve 2 of the hopper opens through the link 9 to fill the solution of hydraulic cylinder 4 of the pump with the mixture and the periodic cycle of pump operation is repeated.

The rocker mechanism allows for a larger phase angle ${\phi }_p$ during the working stroke than the phase angle ${\phi }_x$ during the idle stroke of the crank slider 11: ${\phi }_p>{\phi }_x$. Therefore, with uniform rotational angular motion of the crank 12 around its axis, the piston speed parameters $V_p$ in the operating mode under load when extruding the mixture solution will be significantly lower than during the piston's idle stroke: $V_p<V_x$. This will result in energy savings in the electric motor.

The magnitude of the stroke displacement $S$ of piston 5 in the pump’s hydraulic cylinder depends on the length of the radius $R$ and the swing angle $\phi$ of the link. As a result, we determine the range of movement of the apex of point $B$ of link 10 along the straight line $S=B{B}_1=D{D}_1$. Here, the stroke length $S$ is obtained from the swing angle $\phi$ of the link from the support point 14:

where $R$ is the radius of the swinging link 10 $R=$1.25 m; $\phi$ is the swing angle of the link, rad.

The swing angle $\phi$ of the rocker arm 10 depends on the location of the axis $O_2$ rotation of crank 12 and point $O_2$ supports 14, wings 10:

where $K$ is the coefficient of change in the average speed and displacement $S$ of the end $B$ of the linkage 10, $K=$1.5…3, we select $K=$2. Substituting the value $K=$2 into Eq. (2) and (1) we obtain $\phi =$ 60° and $S=$1.25 m. When synthesizing the linkage mechanism, we determine the center distance ${\alpha }_w=O_1{O}_2$ of the linkage mechanism:

where $r$ is the crank radius, $r=$0.35 m.

Substituting the numerical values into Eq. (3), we obtain ${\alpha }_w=$0.7 m.

We determine the phase angles of slider 11 of the rocker mechanism:

– For the working stroke of the pump piston:

– For idle stroke of the pump piston:

Substituting the numerical values into Eq. (4) and (5), we obtain ${\phi }_p=$ 240° and ${\phi }_x=$ 120°, here the coefficient of change in the average speed of the rocker arm will be $K={\phi }_p/{\phi }_x=\text{2}$. With constant rotation of the crank 12 with an angular velocity $\omega =const$, the rocker mechanism allows to obtain a variable $V=Var$ reduced speed $V_p$ of the working stroke of the piston compared to the speed $V_x$ of the idle stroke of the pump piston:, since asymmetrical phase angles ${\phi }_p$ of the working and ${\phi }_x$ idle strokes of the rocker-piston $V_p=V_x$ mechanism will occur: ${\phi }_p=$240°$>{\phi }_x=$ 120°.

Fig. 1Kinematic diagram of pump

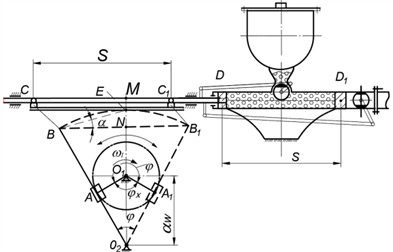
a) Kinematic diagram of a scotch-piston pump

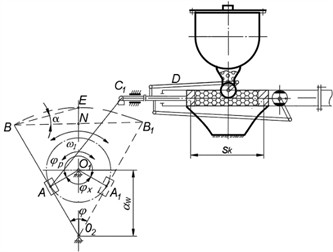
b) Kinematic diagram of a crank-scotch piston pump

The displacement of the piston $S_K$ in the pump hydraulic cylinder in the crank-link mechanism (Fig. 1(b)) is determined depending on the length of the crank radius:

where is the radius of the crank, $r=$ 35 m substituting, we get $S_K=$ 0.7 m.

The speed of movement of point $A$ of the crank of the main link of the rocker mechanism is determined by the formula:

where ${\omega }_1$ is the angular velocity of the crank rotation, ${\omega }_1=\frac{\pi \bullet n_1}{30}$rad/s, where $n_1$ is the crank rotation frequency, $n_1=$ 60 rev/min, $r$ is the crank radius, $r=$0.35 m, $\pi =$ 3.14.

Substituting the numerical values into Eq. (6) we obtain:

Speed of movement $V_A$ points $A$ of the crank of the main link of the rocker mechanism (Fig. 1(b)) is determined by the formula $V_A={\omega }_{1}r$, where is the angular velocity of rotation of point $A$ of the crank, ${\omega }_1=$6.28 rad/s, here is the rotation frequency of the crank, $n=$60 rev/min, $\pi =$ 3.14, ${\omega }_1=\frac{\pi \cdot n_1}{30}$ rad/s.

Substituting numerical values into the Eq. (7) we get: ${\omega }_1=$ 6.28 rad/s, $V_A=$2.2 m/s.

From Fig. 1(a), we determine the maximum angular velocity ${\omega }_{max}$ of the B-link peak. Thus, during horizontal movement, $B$…$B_1$ will be in the same vertical position of the mechanism as point $A$ of slider 11 of crank 12 and coincide with the vertical level at point $N$. From the relationship, we obtain, where the angle is the angle of inclination between $BN$ and $BE$, $\alpha =$ 0.1736 rad, ${\omega }_1(0.5R\sin \alpha +a_w+r)=w_{1}r$:

Then, the maximum speed of point $B$ of the link 10 in the working area is determined at the junction of the horizontal $B\dots B_1$ and vertical $0_2\dots 0_1$ movements of the two lines at point $N:V_B$:

Substituting the numerical values into Eq. (9), we obtain the calculated value of the maximum speed of the top of point $B$ of the slide, $V_p=$2.37 m/s accordingly, the maximum speed $V_p=V_{max}$ the pump piston will be equal ${V=V}_p=$2.37 m/s.

The maximum angular velocity of the link $B$ in the idle zone of the piston pump will be ${\omega }_x$:

Also, the maximum speed $V_x$ points $B$ of the linkage and the pump piston in idle mode will be:

Substituting the numerical values into Eq. (11) we obtain $V_x=$ 5.9 m/s.

We select the kinematic diagram for the displacement of point $C$ ($D$) of the slider (piston) (Fig. 2(a)) in the following scales: the distance of the piston travel length $m_L=m_S=$0.01 m/mm, the angle of rotation of the crank and time: ${\mu }_t=$0.0067 s/mm, where ${\omega }_1$ is the angular velocity of the crank, ${\omega }_1=$6.28 rad/s, $t$ is the time of one revolution of the crank, $t=$0.0014 s, and $S$ is the length of the segment along the abscissa coordinate axis, we take $S=$150 mm, substituting the numerical values, we get: ${\mu }_t=$ 0.0067 s/mm; ${\mu }_{\phi }=2\cdot \pi /L=$ 6.28/150 = 0.042 rad/mm.

One turn ${\omega }_1$ divide the crank’s circumference into 12 parts and transfer them to the diagram along the abscissa axis of a flat coordinate system, and equate this segment to an angle of ${\phi }_1$, where one division is equal to $\phi =$ 30°. Here, one position of the interval, for example, from the 0 to 2 mark, is equal to the crank rotation angle $\phi =$ 60°. Along the ordinate of the diagram, we plot the displacement of the piston stroke $S_D$ from point $D$ to point $D_1$, the maximum interval is equal to $S_D=$1.25 m. The diagram shows asymmetrical phase angles of the working stroke 8 and the idle stroke of the piston 4: $\phi =8\phi$ = 240°, $\phi =4\phi$ = 120°.

To determine the speed and to calculate the piston link acceleration, we first differentiated the $S_D\left(\phi \right)$ diagram, then the $V_D\left(\phi \right)$ diagram. The velocity scaling factor of the diagram (Fig. 2(b)) is, where $P_V$ is the pole distance, $P_V=$25 mm; substituting, we obtain. We construct the acceleration diagram ${\alpha }_D={\alpha }_D\left(t\right)$ (Fig. 2(c)) by graphically differentiating the diagram with respect to time $t$$V_D=V_D\left(t\right)$. The acceleration scaling factor is, where $P_a$ is the pole distance, $P_a=$ 8 mm; substituting the numerical values, we obtain. The numerical values obtained for the piston link position points are summarized in Table 1: ${\mu }_{\nu }={\mu }_L/{\eta }_t\cdot P\nu$, ${\mu }_{\nu }=$ 0.06 m/s, ${\mu }_{\nu }={\mu }_a/{\eta }_t\cdot P_a$, ${\mu }_a=$ 0.891 m/s².

Maximum piston speed the obtained values of the piston-rocker pump in the working zone were in position 5 (Fig. 2(b)) $V_p=$2.51 m/s, and in the idle zone $V_x=$5.1 m/s, and the piston acceleration in position 5 was ${\alpha }_p=$35.64 m/s² and in position 12 of idle running ${\alpha }_x=$50.78 m/s². Also, the maximum piston speed of the crank-rocker pump was: $V_p=$2.05 m/s and $V_x=$2.1 m/s, and the maximum acceleration in position 9 was ${\alpha }_x=$16.04 m/s² and in position 12 of idle running ${\alpha }_x=$16.93 m/s².

Fig. 2Kinematic diagram of the piston of a spool-piston pump: 1 – kinematic diagram of a scotch-piston pump, 2 – kinematic diagram of a crank-scotch piston pump

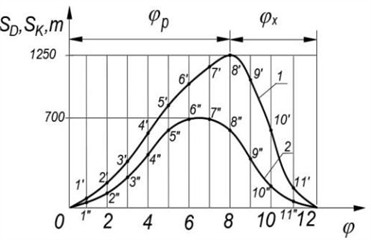
a) The displacement $S_D$ of the piston stroke

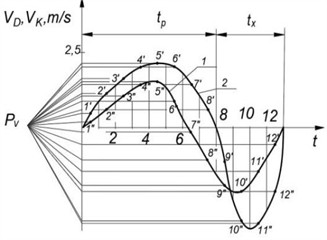
b) The linear velocity $V_D$ of the piston

c) The acceleration $a_D$ of the piston

The percentage difference in maximum speeds was obtained. In the parameters of the pump piston, by comparing theoretical calculations with the obtained results of the numerical values of the kinematic diagrams (Fig. 2(b)) for the rocker-piston mechanism:

– For the working stroke of the piston:

– For idle stroke of the piston:

4. Conclusions

The kinematic diagram of a rocker-piston pump was investigated, in which asymmetric phase angles of the working and idle strokes of the rocker mechanism crank were identified, which led to an increase in the length of the working stroke of the piston by several times than that of serial pumps, which leads to an increase in the pump performance ${\phi }_p=$ 240°$>{\phi }_x=$ 120°.

Based on the constructed kinematic diagrams, their maximum speeds in the working zone and in the idle zone were obtained $V_p=$2.51 m/s; $V_x=$5.6 m/s.

Reducing the piston speed in the pump’s hydraulic cylinder helps reduce piston wear and abrasion of the hydraulic pump surface. Also, reducing the average speed in the piston's working stroke reduces the electric motor's power consumption.

5. Future possibilities

In future studies, the graph-analytical model could be extended to include dynamic forces, friction, and elastic deformations to more fully simulate real-world conditions.

Refining the choice of asymmetric phase angles (${\phi }_p$ and ${\phi }_x$) through computational optimization can improve the balance between performance and energy efficiency.

The implementation of sensors and microcontrollers for adaptive crankshaft control can provide intelligent adjustment of piston movement depending on load and flow.

Creating a digital twin of a pumping mechanism will enable remote monitoring, fault prediction, and performance optimization using real-time data.

The rocker-piston concept can be tested and adapted for high pressure applications such as oil production or chemical injection systems.

Further research will allow us to analyze the impact of reducing piston speed on energy consumption, which will potentially allow us to implement new energy-saving operating modes.

The creation of a physical prototype based on the proposed model will allow for experimental confirmation of the calculated kinematic parameters and wear characteristics.

The use of wear-resistant coatings or advanced composite materials on piston and cylinder components can extend service life and reduce maintenance.