Random parametric nonlinear vibrations of a discrete mechanical system protected from vibration

Dusmatov, Olimjon; Khodjabekov, Muradjon; Ashurov, Bakhtiyor

doi:10.21595/vp.2025.25300

Vibroengineering Procedia

Browse Procedia

Published: December 22, 2025

Check for updates

Random parametric nonlinear vibrations of a discrete mechanical system protected from vibration

Olimjon Dusmatov¹

Muradjon Khodjabekov²

Bakhtiyor Ashurov³

¹Samarkand State University after named Sharof Rashidov, 141602, Samarkand, Uzbekistan

^{2, 3}Samarkand State Architecture and Construction University, 140147, Samarkand, Uzbekistan

Corresponding Author:

Olimjon Dusmatov

Cite the article Download PDF

Downloads 18

Abstract

In this work, the issue of checking the dynamics of nonlinear vibrations of a mechanical system protected from vibrations in case of random parametric excitations is considered. Using the Ito method, the analytical expressions of the mean square values of the absolute accelerations of the mechanical system and the dynamic absorber were determined. Statistical linearization method based on Davidenko's hypothesis was used to determine mean squared values. The average square value change of the random parametric vibration of the mechanical system protected against vibrations with the dynamic absorber at different values of the parameter describing the width of the vibration spectrum was analysed. It is shown that if the parameter describing the width of the vibration spectrum is taken smaller, the mean square value of the random parametric vibration of the protected object combined with the dynamic absorber will have a smaller vibration. At different values of the parameter of the hysteresis loop, the change of the mean square value of the random parametric vibration was analysed and appropriate conclusions were drawn.

1. Introduction

Damping of harmful vibrations of mechanical systems under the influence of random parametric excitations is one of the urgent problems. Mathematical modeling of the materials of mechanical system elements, taking into account the elastic dissipative characteristics of the hysteresis type, and choosing their optimal parameters are important issues.

The use of stochastic methods in solving the problems of protection of various types of mechanical systems from harmful vibrations is considered in works [1]-[6].

In the works [7]-[11], the issue of dynamics and stability of nonlinear vibrations of a hysteresis-type elastic dissipative characteristic mechanical system combined with a liquid section dynamic absorber under the influence of random parametric excitations was considered. Using the method of stochastic averaging, the system of differential equations of motion is presented as a system of Ito equations. In this case, a random function was selected and the values at which stability conditions were determined through the spectral density of longitudinal and transverse vibrations in white noise excitations.

In the article [12], the parametric vibration of a ship under the influence of random excitations caused by waves is studied. The differential equation of the parametric vibration of a ship under the influence of random excitations is constructed taking into account nonlinear damping and ship speed. The density function corresponding to the stability vibrations is obtained, and the correctness of the results is shown by numerical simulation.

The work [13] considers the damping characteristics of a passive fluid-coupled dynamic absorber, which is effective in damping harmful vibrations of engineering systems. The issue of optimizing it to minimize the vibration amplitude over a wide range of frequencies, taking into account the maximum fluid lift limit on the columns, is considered and solved using numerical methods.

In works [14]-[16] mathematical modeling of nonlinear mechanical systems, study of dynamics and checking of stability of motions and instructions for selection of parameters corresponding to stable motions, in particular mechanical system materials are given. Modal mass and modal stiffness expressions are analytically expressed. With their help, the issues of choosing and modeling system materials were also solved.

In the articles [17]-[19], nonlinear parametric vibrations of a beam with a dynamic absorber under the influence of external excitations are studied taking into account the elasticity and damping properties of materials. The linearization method is used to solve nonlinear differential equations of motion of the system. The non-stationary and stationary values of the amplitude and phase of vibrations are determined analytically. The stability conditions of stationary motion are obtained based on the Rous-Hurwitz criterion. The effect of changing the parameter values on the amplitude-frequency characteristic constructed based on the calculation results is shown.

In the article [20], bridges reinforcement for usable geometric linear not been cable bending angle and bridge vibration the secret of the effect into account received without random movement sunder the influence parametric vibrations studied. Random in motion cable soft characteristic maybe as maybe and bridge plate joint movement differential equations system. This system of differential equations is transformed into Ito differential equations and the Milstein-Platen method is used for numerical analysis. In order to avoid the influence of the parametric diffusion coefficient in Ito differential equations, an iterative method for solving random differential vibrations of the beam is proposed. The amplitude, spectral density and density function changes are analyzed and the results obtained by this method are compared with those obtained by the Gaussian method.

2. Materials and methods

In this work, the problem of studying the dynamics of vibrations of a hysteresis-type elastic dissipative mechanical system with a dynamic absorber under the influence of random parametric excitations was considered (Fig. 1). The dissipative properties of the materials of the elastic damping elements of the mechanical system and the dynamic absorber are obtained in the hysteresis type. Connections between stress and deformation are obtained by nonlinear non-single-valued functions and expressed by linear functions using the statistical linearization method.

Fig. 1A mechanical system protected from vibrations

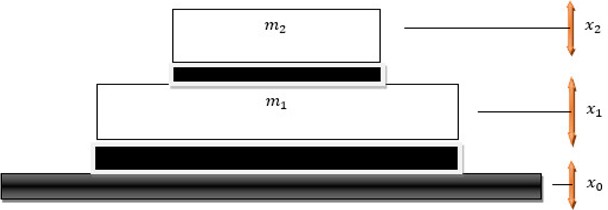
The system of differential equations of motion of a mechanical system protected from vibrations is as follows:

1

m_{1} {\ddot{x}}_{1} + c_{1} (1 - η_{1} + i η_{2}) x_{1} - c_{2} (1 - ν_{1} + i ν_{2}) x_{2} = {- c}_{1} ξ_{0} (t) x_{1} (t),

m_{2} {\ddot{x}}_{1} + m_{2} {\ddot{x}}_{2} + c_{2} (1 - ν_{1} + i ν_{2}) x_{2} = 0,

where $m_{1}$ , $m_{2}$ are the masses of the protected object and the dynamic absorber, respectively, $x_{1}$ , $x_{2}$ are the displacement coordinates of the protected object and the dynamic absorber; $c_{1}$ , $c_{2}$ are elasticity coefficients of the object to be protected and the dynamic absorber; $i^{2} =$ –1; $η_{1}$ , $η_{2}$ are linearization coefficients representing the dissipative properties of the material of the elastic damping element of the object; $ν_{1}$ , $ν_{2}$ are linearization coefficients representing the dissipative properties of the material of the elastic damping element of the dynamic absorber [1]; $ξ_{0} (t)$ is a variable representing a stationary normal random process.

Let’s express the differential equations of motion of the mechanical system as follows:

2

{\ddot{x}}_{1} + ω_{1}^{2} (1 - η_{1} + i η_{2}) x_{1} - μ ω_{2}^{2} (1 - ν_{1} + i ν_{2}) x_{2} = - {ω_{1}^{2} ξ}_{0} (t) x_{1} (t),

{\ddot{x}}_{1} + {\ddot{x}}_{2} + ω_{2}^{2} (1 - ν_{1} + i ν_{2}) x_{2} = 0,

Where $μ = m_{2} / m_{1}$ ; $ω_{1}^{2} = c_{1} / m_{1}$ , $ω_{2}^{2} = c_{2} / m_{2} .$

The solution of the system of differential Eq. (2) is looked for in the following form:

3

x_{1} = A e^{i ω t} + B e^{- i ω t}, x_{2} = C e^{i ω t} + D e^{- i ω t},

where $ω$ is the frequency of vibrations; $A = A (t)$ , $B = B (t)$ , $C = C (t)$ , $D = D (t)$ are slowly variable functions, and the amplitude value of random parametric excitations of the mechanical system is $〈x_{1 a}〉 = 2 \sqrt{〈A (t)〉 〈B (t)〉}$ satisfies the condition.

Taking into account that $A$ , $B$ , $C$ , $D$ are slowly variable functions, if the variables Eq. (3) and their respective derivatives are put into the system of differential Eq. (2), it is possible to get the following system of differential equations of the first order:

4

\dot{A} = \frac{1}{2 i ω} ((ω^{2} {{- ω}_{1}^{2} ξ}_{0} (t) - ω_{1}^{2} (1 - η_{1} + i η_{2})) (A + B e^{- 2 i ω t}) + μ ω_{2}^{2} (1 - ν_{1} + i ν_{2}) (C + D e^{- 2 i ω t})),

\dot{B} = - \frac{1}{2 i ω} ((ω^{2} {{- ω}_{1}^{2} ξ}_{0} (t) - ω_{1}^{2} (1 - η_{1} + i η_{2})) (A e^{2 i ω t} + B) + μ ω_{2}^{2} (1 - ν_{1} + i ν_{2}) (C e^{2 i ω t} + D)),

\dot{C} = \frac{1}{2 i ω} ((ω^{2} + {(μ + 1) ω}_{2}^{2} (1 - ν_{1} + i ν_{2})) (D e^{- 2 i ω t} + C) + (- {ω_{1}^{2} ξ}_{0} (t) + ω_{1}^{2} (1 - η_{1} + i η_{2})) (A + B e^{- 2 i ω t})),

\dot{D} = - \frac{1}{2 i ω} ((ω^{2} + {(μ + 1) ω}_{2}^{2} (1 - ν_{1} + i ν_{2})) (C e^{2 i ω t} + D) + (- {ω_{1}^{2} ξ}_{0} (t) + ω_{1}^{2} (1 - η_{1} + i η_{2})) (A e^{2 i ω t} + B)) .

In stochastic processes, the variables of the system of Eq. (4) satisfy the Ito equations [6]. Therefore, use the stochastic averaging method and change the system of Eq. (4) to the system of Ito equations.

5

\frac{d 〈A〉}{d t} = p_{1} 〈A〉 + \frac{π}{2} p_{5}^{2} (S (0) - i ψ (2 ω)) 〈A〉 + p_{2} 〈C〉,

\frac{d 〈B〉}{d t} = - p_{1} 〈B〉 - \frac{π}{2} p_{5}^{2} (S (2 ω) - S (0)) 〈B〉 - p_{2} 〈D〉,

\frac{d 〈C〉}{d t} = p_{4} 〈A〉 + \frac{π}{2} p_{5}^{2} (S (0) - i ψ (2 ω)) 〈A〉 + p_{3} 〈C〉,

\frac{d 〈D〉}{d t} = - p_{4} 〈B〉 - \frac{π}{2} p_{5}^{2} (S (2 ω) - S (0)) 〈B〉 - p_{3} 〈D〉,

where:

p_{1} = \frac{ω^{2} - ω_{1}^{2} (η_{1} + i η_{2})}{2 i ω}, p_{2} = \frac{{μ ω}_{2}^{2} (ν_{1} + i ν_{2})}{2 i ω}, p_{3} = \frac{ω^{2} + (1 + μ) ω_{2}^{2} (ν_{1} + i ν_{2})}{2 i ω},

p_{4} = \frac{ω_{1}^{2} (η_{1} + i η_{2})}{2 i ω}, p_{5} = - \frac{ω_{1}^{2}}{2 i ω},

and $S (0)$ , $S (2 ω)$ , $ψ (2 ω)$ are defined as the spectral density of a stationary normal random process $ξ_{0} (t)$ as follows [6]:

S (2 ω) = \frac{1}{π} \int_{- \infty}^{0} R (τ) c o s ω τ d τ, ψ (2 ω) = \frac{1}{π} \int_{- \infty}^{0} R (τ) s i n ω τ d τ,

Where $R (τ) = E [ξ_{0 n} (t) ξ_{0 m} (t + τ)] = 〈ξ_{0 n} (t) ξ_{0 m} (t + τ)〉$ is correlation function.

Let’s look for the solution of the system of Eq. (5) as follows:

6

A = A_{0} e^{λ t}, B = B_{0} e^{λ t}, C = C_{0} e^{λ t}, D = D_{0} e^{λ t},

where $A_{0}$ , $B_{0}$ , $C_{0}$ , $D_{0}$ are the amplitude values of the random parametric excitations of the mechanical system; $λ$ is a characteristic number.

Let’s put the Eq. (6) into the system of Eq. (5) and from the condition of having a non-zero solution, the determinant form of the characteristic equation of the system can be formed as follows:

7

[\begin{matrix} a_{11} + λ & \dots & a_{14} \\ ⋮ & ⋱ & ⋮ \\ a_{41} & \dots & a_{44} + λ \end{matrix}] = 0,

where:

a_{11} = p_{1} + \frac{π}{2} p_{5}^{2} (S (0) + i ψ (2 ω)), a_{12} = 0; a_{13} = p_{2}, a_{14} = 0,

a_{21} = 0; a_{22} = - p_{1} - \frac{π}{2} p_{5}^{2} (S (2 ω) - S (0)), a_{23} = 0, a_{24} = - p_{2},

a_{31} = p_{4} + \frac{π}{2} p_{5}^{2} (S (0) + i ψ (2 ω)); a_{32} = 0, a_{33} = p_{3}, a_{34} = 0,

a_{41} = 0; a_{42} = - p_{4} - \frac{π}{2} p_{5}^{2} (S (2 ω) - S (0)), a_{43} = 0, a_{44} = - p_{3} .

Using the determinant Eq. (7), it is possible to form the following two characteristic equations:

8

λ^{4} - (a_{11} + a_{22}) λ^{3} + (a_{11} a_{22} - a_{31} p_{2} + a_{42} p_{2} - p_{3}^{2}) λ^{2} + (- a_{11} a_{42} p_{2} + a_{11} p_{3}^{2} + a_{22} a_{31} p_{2} + (- a_{11} a_{42} p_{2} + a_{11} p_{3}^{2} + a_{22} a_{31} p_{2} + a_{22} p_{3}^{2} - a_{31} p_{2} p_{3} - a_{42} p_{2} p_{3}) λ + a_{11} a_{22} p_{3}^{2} + a_{11} a_{42} p_{2} p_{3} + a_{22} a_{31} p_{2} p_{3} - a_{31} a_{42} p_{2}^{2} = 0 .

The obtained characteristic equations allow checking the dynamics and stability of the mechanical system protected from vibrations.

3. Result and discussion

The characteristic equations are quadratic equations. Let’s identify their roots:

9

λ_{1} = \frac{1}{2} (a_{11} + p_{3}) + \frac{1}{2} \sqrt{{(a_{11} - p_{3})}^{2} + 4 a_{31} p_{2}},

λ_{2} = \frac{1}{2} (a_{11} + p_{3}) - \frac{1}{2} \sqrt{{(a_{11} - p_{3})}^{2} + 4 a_{31} p_{2}},

λ_{3} = \frac{1}{2} (a_{22} - p_{3}) + \frac{1}{2} \sqrt{{(a_{22} + p_{3})}^{2} - 4 a_{42} p_{2}},

λ_{4} = \frac{1}{2} (a_{22} - p_{3}) - \frac{1}{2} \sqrt{{(a_{22} + p_{3})}^{2} - 4 a_{42} p_{2}} .

Using Moivre’s formula for expressions involving roots of the characteristic Eq. (9), we determine their values. In this case, the roots of Eq. (9) will be as follows:

10

λ_{1} = \frac{1}{2} (p_{1} + \frac{π}{2} p_{5}^{2} (S (0) + i ψ (2 ω)) + p_{3}) + \frac{1}{8 ω^{2}} (α_{1} + i β_{1}),

λ_{2} = \frac{1}{2} (p_{1} + \frac{π}{2} p_{5}^{2} (S (0) + i ψ (2 ω)) + p_{3}) - \frac{1}{8 ω^{2}} (α_{1} + i β_{1}),

λ_{3} = \frac{1}{2} (- p_{1} - \frac{π}{2} p_{5}^{2} (S (2 ω) - S (0)) - p_{3}) + \frac{1}{8 ω^{2}} (α_{2} + i β_{2}),

λ_{4} = \frac{1}{2} (- p_{1} - \frac{π}{2} p_{5}^{2} (S (2 ω) - S (0)) - p_{3}) - \frac{1}{8 ω^{2}} (α_{2} + i β_{2}),

where:

α_{1} = 2^{- \frac{1}{2}} {(a_{1}^{2} + b_{1}^{2})}^{\frac{1}{4}} {({(a_{1}^{2} + b_{1}^{2})}^{\frac{1}{2}} + a_{1})}^{\frac{1}{2}}, α_{2} = 2^{- \frac{1}{2}} {(a_{2}^{2} + b_{2}^{2})}^{\frac{1}{4}} {({(a_{2}^{2} + b_{2}^{2})}^{\frac{1}{2}} + a_{2})}^{\frac{1}{2}},

β_{1} = 2^{- \frac{1}{2}} {(a_{1}^{2} + b_{1}^{2})}^{\frac{1}{4}} {({(a_{1}^{2} + b_{1}^{2})}^{\frac{1}{2}} - b_{1})}^{\frac{1}{2}}, β_{2} = 2^{- \frac{1}{2}} {(a_{2}^{2} + b_{2}^{2})}^{\frac{1}{4}} {({(a_{2}^{2} + b_{2}^{2})}^{\frac{1}{2}} - b_{2})}^{\frac{1}{2}},

a_{1} = 16 ((η_{2}^{2} - {(1 - η_{1})}^{2}) ω_{1}^{4} - 6 ((1 - η_{1}) (1 - ν_{1}) + η_{2} ν_{2}) (μ + \frac{1}{3}) ω_{2}^{2} ω_{1}^{2} - {(1 + μ)}^{2} ({(1 - ν_{1})}^{2} - ν_{2}^{2}) ω_{2}^{4}) ω^{2} + 8 ω_{1}^{4} π

\times (((1 - η_{1}) ω_{1}^{2} - {(1 - ν_{1}) ω}_{2}^{2} (μ - 1)) ψ (2 ω) + (η_{2} ω_{1}^{2} - ν_{2} ω_{2}^{2} (μ - 1)) S (0)) ω - ({(ψ (2 ω))}^{2} - {S (0)}^{2}) {π^{2} ω}_{1}^{8},

b_{1} = - 32 ((1 - η_{1}) η_{2} ω_{1}^{4} + 3 (η_{2} (1 - ν_{1}) + ν_{2} (1 - η_{1})) (μ + \frac{1}{3}) ω_{2}^{2} ω_{1}^{2} + {(1 + μ)}^{2} ω_{2}^{4} (1 - ν_{1}) ν_{2}) ω^{2} + 8 ω_{1}^{4} π

\times (((1 - η_{1}) ω_{1}^{2} - {(1 - ν_{1}) ω}_{2}^{2} (μ - 1)) ψ (2 ω) + (η_{2} ω_{1}^{2} - ν_{2} ω_{2}^{2} (μ - 1)) S (0)) ω - ({(ψ (2 ω))}^{2} - {S (0)}^{2}) {π^{2} ω}_{1}^{8} \times ((η_{2} ω_{1}^{2} - ν_{2} ω_{2}^{2} (μ - 1)) ψ (2 ω) + (- (1 - η_{1}) ω_{1}^{2} + (1 - ν_{1}) ω_{2}^{2} (μ - 1)) s (0)) ω + 2 ω_{1}^{8} π^{2} S (0) ψ (2 ω),

a_{2} = 16 ((η_{2}^{2} - {(1 - η_{1})}^{2}) ω_{1}^{4} - 6 ((1 - η_{1}) (1 - ν_{1}) - η_{2} ν_{2}) ω_{2}^{2} (μ + \frac{1}{3}) ω_{1}^{2} - {(1 + μ)}^{2} ω_{2}^{4} ({(1 - ν_{1})}^{2} - ν_{2}^{2})) ω^{2} + 8 ω_{1}^{4} π \times (η_{2} ω_{1}^{2} - ν_{2} ω_{2}^{2} (μ - 1)) (S (2 ω) - S (0)) ω + π^{2} ω_{1}^{8} {(S (0) - S (2 ω))}^{2};

b_{2} = - 32 ((1 - η_{1}) η_{2} ω_{1}^{4} + 3 (η_{2} (1 - ν_{1}) + ν_{2} (1 - η_{1})) (μ + \frac{1}{3}) ω_{2}^{2} ω_{1}^{2} + {(1 + μ)}^{2} ω_{2}^{4} (1 - ν_{1}) ν_{2}) ω^{2} + + 8 ω_{1}^{4} π (- (1 - η_{1}) ω_{1}^{2} + (1 - ν_{1}) ω_{2}^{2} (μ - 1)) (S (2 ω) - S (0)) ω .

The roots of the identified characteristic equation allow for the examination of the mean square expectations and the stability of a mechanical system protected against damped oscillations.

According to stability theory, for a damped motion to be asymptotically stable, it is sufficient that the real parts of the characteristic equation’s roots are negative. Based on this, we determine the boundary between stable and unstable motions:

11

- ω_{1}^{2} ν_{2} + π p_{5}^{2} ω S (0) + (1 + μ) ω_{2}^{2} η_{2} + \frac{1}{2 ω} α_{1} = 0,

- ω_{1}^{2} ν_{2} + π p_{5}^{2} ω S (0) + (1 + μ) ω_{2}^{2} η_{2} - \frac{1}{2 ω} α_{1} = 0,

ω_{1}^{2} ν_{2} - π p_{5}^{2} ω (S (2 ω) - S (0)) - (1 + μ) ω_{2}^{2} η_{2} + \frac{1}{2 ω} α_{2} = 0,

ω_{1}^{2} ν_{2} - π p_{5}^{2} ω (S (2 ω) - S (0)) - (1 + μ) ω_{2}^{2} η_{2} - \frac{1}{2 ω} α_{2} = 0 .

By squaring the Eq. (11), we can reduce them to the following two equations:

12

8 ω^{2} {(- ω_{1}^{2} ν_{2} + π p_{5}^{2} ω S (0) + (1 + μ) ω_{2}^{2} η_{2})}^{2} - {(a_{1}^{2} + b_{1}^{2})}^{\frac{1}{2}} ({(a_{1}^{2} + b_{1}^{2})}^{\frac{1}{2}} + a_{1}) = 0,

8 ω^{2} {(ω_{1}^{2} ν_{2} - π p_{5}^{2} ω (S (2 ω) - S (0)) - (1 + μ) ω_{2}^{2} η_{2})}^{2} - {(a_{2}^{2} + b_{2}^{2})}^{\frac{1}{2}} ({(a_{2}^{2} + b_{2}^{2})}^{\frac{1}{2}} + a_{2}) = 0 .

From the Eq. (12), it is possible to determine the mean square values $σ_{x_{1}}$ ,and $σ_{x_{2}}$ for the considered system.

N. Davidenko’s hypothesis is used for linearization of hysteresis-type nonlinearity. According to it, the linearization coefficients are as follows [1]:

13

η_{1} = \frac{η (n - 1) Г (\frac{n + 3}{2})}{π (n + 1) B (n, n)} 2^{\frac{3 - n}{2}} {σ_{x_{1}}}^{n - 1}, η_{2} = \frac{η (n - 1) Г (\frac{n + 3}{2})}{π (n + 1) n} 2^{\frac{3 n + 1}{2}} {σ_{x_{1}}}^{n - 1},

where $η$ , $n$ are parameters of the hysteresis loop; $Г (\frac{n + 3}{2})$ and $B (n, n)$ are alpha and beta functions, respectively.

For the case when $n =$ 2, based on Eq. (12), we write the linearization coefficients according to Davidenko’s hypothesis as follows [1]:

14

η_{1} = \frac{η Г (\frac{5}{2})}{3 π B (2,2)} 2^{\frac{1}{2}} σ_{x_{1}} = C_{11} σ_{x_{1}}, η_{2} = \frac{η Г (\frac{5}{2})}{6 π} 2^{\frac{7}{2}} σ_{x_{1}} = C_{21} σ_{x_{1}},

ν_{1} = \frac{η_{0} Г (\frac{5}{2})}{3 π B (2,2)} 2^{\frac{1}{2}} σ_{x_{2}} = C_{31} σ_{x_{2}}, ν_{2} = \frac{η_{0} Г (\frac{5}{2})}{6 π} 2^{\frac{7}{2}} σ_{x_{2}} = C_{41} σ_{x_{2}},

where $C_{11} = 1.196826491 η;$ $C_{21} = 0.7978843277 η;$ $C_{31} = 1.196826491 η_{0};$ $C_{41} = 0.7978843277 η_{0} .$

The Eq. (12), together with the linearization coefficients Eq. (14), represent bivariate functions with respect to the root-mean-square values $σ_{x_{1}}$ , and $σ_{x_{2}}$ . They allow evaluating the dynamics of random parametric vibrations in a mechanical system protected against damped oscillations for various parameter values.

If we accept the linearization coefficients Eq. (14) for Eq. (12), then we obtain the following:

15

\sum_{k = 0}^{8} H_{1 k} σ_{x_{2}}^{k} = 0, \sum_{k = 0}^{8} H_{2 k} σ_{x_{2}}^{k} = 0 .

In this case, the coefficients $H_{1 k}$ and $H_{2 k}$ are determined depending on both the system parameters from Eq. (12) and the root-mean-square value $σ_{x_{1}}$ , and $σ_{x_{2}}$ . From Eq. (15), the equality $H_{16} - H_{26} = 0$ yields the following expression:

16

H_{2} σ_{x_{1}}^{2} + H_{1} σ_{x_{1}} + H_{0} = 0,

where:

H_{2} = - \frac{{(3 μ + 1)}^{2}}{6} (2 C_{11} C_{31}^{2} C_{41} - C_{11} C_{41}^{3} + C_{21} C_{31}^{3} - C_{21} C_{31} C_{41}^{2}) C_{21} C_{41}^{2} ω_{1}^{2} {(4 ω^{2} + q^{2})}^{2} q ω^{2},

H_{1} = (4 ω^{2} + q^{2}) ω {(8 ω^{2} + q^{2}) σ_{ξ}^{2} ω_{1}^{4} (C_{11} C_{41} (\frac{1}{16} (\frac{7}{6} μ^{2} - μ - \frac{1}{2}) + {\frac{1}{24} C}_{31}^{2} C_{41}^{2} (3 μ^{2} - 4 μ - 2) + \frac{7}{96} C_{31}^{4}) + + \frac{1}{64} C_{21} C_{31}^{5} (μ + \frac{1}{3}) (μ - 1)) + (4 ω^{2} + q^{2}) C_{21} C_{41}^{3} q ω (μ + \frac{1}{3}) (- \frac{3}{2} (μ + \frac{1}{3}) ω_{1}^{2} C_{41}^{2} + \frac{1}{2} ω_{2}^{2} C_{41}^{3} {(μ + 1)}^{2} + 3 C_{31}^{2} (μ + \frac{1}{3}) ω_{1}^{2} + C_{31}^{2} ω_{2}^{2} {(μ + 1)}^{2} - σ_{ξ}^{2} ω_{1}^{4} C_{21} C_{31} C_{41}^{2} (\frac{1}{12} ω^{2} C_{41}^{2} (- {\frac{13}{2} μ}^{2} + 7 μ + \frac{7}{2}) + \frac{1}{96} q^{2} C_{41}^{2} \times (\frac{11}{2} μ^{2} - μ - \frac{1}{2}) {+ \frac{1}{3} ω}^{2} C_{31} ({7 μ}^{2} - 4 μ - 2) + \frac{1}{24} q^{2} C_{31} (\frac{17}{2} μ^{2} - 5 μ - \frac{5}{2}))\},

H_{0} = - \frac{1}{32} σ_{ξ}^{2} (8 ω^{2} + q^{2}) ω_{1}^{2} \{(4 ω^{2} + q^{2}) C_{41} ω (C_{41}^{4} (μ^{3} ω_{2}^{2} + (\frac{7}{3} ω_{1}^{2} + ω_{2}^{2}) μ^{2} + (- 2 ω_{1}^{2} - ω_{2}^{2}) μ {- ω}_{1}^{2} - ω_{2}^{2}) + \frac{8}{3} C_{31}^{2} C_{41}^{2} (μ^{3} ω_{2}^{2} + (\frac{3}{2} ω_{1}^{2} + ω_{2}^{2}) μ^{2} + (- 2 ω_{1}^{2} - ω_{2}^{2}) μ - ω_{1}^{2} - ω_{2}^{2}) + (C_{31}^{2} C_{41}^{2} + C_{31}^{4}) (μ^{3} ω_{2}^{2} + (\frac{7}{3} ω_{1}^{2} + ω_{2}^{2}) μ^{2} + (- 2 ω_{1}^{2} - ω_{2}^{2}) μ - ω_{1}^{2} - ω_{2}^{2})) {+ σ}_{ξ}^{2} ω_{1}^{4} q C_{31} (\frac{5}{16} C_{41}^{4} (μ^{2} - \frac{22}{15} μ + 1) + \frac{1}{2} C_{31}^{2} C_{41}^{2} (μ^{2} - \frac{8}{3} μ + 1) + \frac{1}{48} C_{31}^{4} {(μ - 1)}^{2})\} .

From the quadratic Eq. (16):

17

σ_{x_{1}} = \frac{- H_{1} \pm \sqrt{H_{1}^{2} - 4 H_{2} H_{0}}}{{2 H}_{2}} .

In the root-mean-square Eq. (17), we divide both the numerator and denominator of the fraction by $q^{9}$ and write it as follows:

18

σ_{x_{1}} = \frac{- H_{1 *} \pm \sqrt{H_{1 *}^{2} - 4 H_{2 *} H_{0 *}}}{{2 H}_{2 *}},

where:

H_{2 *} = - \frac{{(3 μ + 1)}^{2}}{6} (2 C_{11} C_{31}^{2} C_{41} - C_{11} C_{41}^{3} + C_{21} C_{31}^{3} - C_{21} C_{31} C_{41}^{2}) C_{21} C_{41}^{2} Ω_{1}^{2} {(4 Ω_{0}^{2} + 1)}^{2} Ω_{0}^{2},

H_{1 *} = (4 Ω_{0}^{2} + 1) Ω_{0}^{} {σ_{ξ}^{2} Ω_{1}^{4} (8 Ω_{0}^{2} + 1) (\frac{1}{96} C_{11} C_{41} (7 μ^{2} - 6 μ - 3) (C_{41}^{4} + C_{31}^{4})

+ \frac{1}{24} C_{31}^{2} C_{41}^{3} (3 μ^{2} - 4 μ - 2) + \frac{1}{64} C_{21} C_{31}^{5} (μ + \frac{1}{3}) (μ - 1))

+ (4 Ω_{0}^{2} + 1) C_{21} C_{41}^{3} Ω_{0}^{} (μ + \frac{1}{3}) (Ω_{1}^{2} (μ + \frac{1}{3}) (- \frac{3}{2} C_{41}^{2} + 3 C_{31}^{2}) + Ω_{2}^{2} {(+ 1)}^{2}

\times (- \frac{1}{2} C_{41}^{2} + C_{31}^{2})) + (- Ω_{1}^{4} C_{41}^{5} - Ω_{1}^{4} C_{41}^{4} C_{21} C_{31} σ_{ξ}^{2}) (\frac{1}{12} (- {\frac{13}{2} μ}^{2} + 7 μ + \frac{7}{2}) Ω_{0}^{2} + \frac{1}{96} (\frac{11}{2} μ^{2} - μ - \frac{1}{2}))

{+ Ω}_{1}^{4} C_{41}^{2} C_{31}^{2} C_{21} σ_{ξ}^{2} (\frac{1}{3} ({7 μ}^{2} - 4 μ - 2) Ω_{0}^{2} + \frac{1}{24} (\frac{17}{2} μ^{2} - 5 μ - \frac{5}{2}))\},

H_{0 *} = - \frac{1}{32} σ_{ξ}^{2} (8 Ω_{0}^{2} + 1) Ω_{1}^{2} {(4 Ω_{0}^{2} + 1) Ω_{0} C_{41}

\times ((μ^{3} Ω_{2}^{2} + (\frac{7}{3} Ω_{1}^{2} + Ω_{2}^{2}) μ^{2} + (- 2 Ω_{1}^{2} - Ω_{2}^{2}) μ - Ω_{1}^{2} - Ω_{2}^{2})

\times (C_{41}^{4} + C_{31}^{4}) + \frac{8}{3} C_{31}^{2} C_{41}^{2} (μ^{3} Ω_{2}^{2} + (\frac{3}{2} Ω_{1}^{2} + Ω_{2}^{2}) μ^{2} + (- 2 Ω_{1}^{2} - Ω_{2}^{2}) μ - Ω_{1}^{2} - Ω_{2}^{2})) + Ω_{1}^{4} σ_{ξ}^{2} C_{31} (\frac{5}{16} C_{41}^{4} \times (μ^{2} - \frac{22}{15} μ + 1) + \frac{1}{4} C_{31}^{2} C_{41}^{2} (μ^{2} - \frac{8}{3} μ + 1) + \frac{1}{48})\},

Ω_{0} = \frac{ω}{q}, Ω_{1} = \frac{ω_{1}}{q}, Ω_{2} = \frac{ω_{3}}{q} .

We perform a numerical analysis of the mean square value Eq. (18). In this case, we take the parameters as follows [1]: $σ_{ξ}^{} = \sqrt{10} g$ , $η =$ 5×10⁷ m^-2; $η_{0} =$ 5×10³ m^-2; $η_{1} = 1.196826491 η σ_{x_{1}}$ , $η_{2} = 0.7978843277 η σ_{x_{1}}$ , $ν_{1} = 1.196826491 η_{0} σ_{x_{2}}$ , $ν_{2} = 0.7978843277 η_{0} σ_{x_{2}}$ , $Ω_{1}^{} = ω_{1} / q$ , $Ω_{2}^{} = ω_{2} / q = 0.1$ .

Fig. 2Variation of the root mean square value Eq. (18) defined by the expression

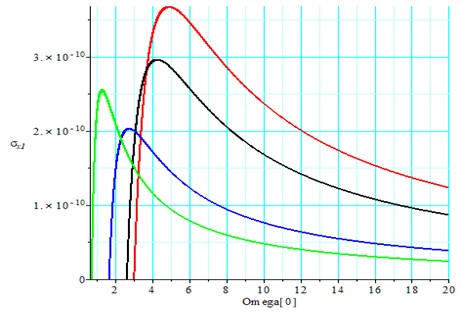
The graph of the root mean square value Eq. (18) will be as shown in Fig. 2.

In Fig. 2 the root mean square value, defined by the given expression (18), is plotted against the dimensionless parameter $Ω_{0}$ for different mass ratios $μ =$ 0; 0.1; 0.4; 0.6 (red, black, blue, green).From this, it can be concluded that the use of a dynamic absorber is effective in suppressing mechanical system vibrations. Specifically, when $μ =$ 0 (red), the root mean square value reaches significantly higher magnitudes compared to other cases. For the cases $μ =$ 0.1; 0.4; 0.6 (black, blue, green), the graphs suggest that $μ =$ 0.4 (blue) is the optimal value, as any increase or decrease from this ratio leads to a rise in the root mean square values. For $μ =$ 0 (red) and $μ =$ 0.4 (blue), the root mean square values are $σ_{x_{1}} =$ 3.75×10^-10 m and $σ_{x_{1}} =$ 2.1×10^-10 m, respectively. The application of the dynamic absorber reduces the root mean square value by a factor of 1.8.

4. Conclusions

The obtained Eq. (18) allow to fully analyze the dynamics of the hysteresis-type elastic dissipative mechanical system protected from vibrations under the influence of random parametric excitations at different values of the parameters, to evaluate the effectiveness of the dynamic absorber, and as a result, to select the optimal structural parameters of the system. At different values of n characterizing the parameter of the hysteresis loop, the mean square value of the random parametric vibrations increases synchronously up to a certain frequency, and from this frequency, a uniform increase violation can be observed. At different values of the parameter $χ$ describing the width of the vibration spectrum, the change in the mean square value of the random parametric vibration is analyzed. According to that it can be concluded that if the parameter describing the width of the vibration.

References

M. A. Pavlovsky, L. M. Ryzhkov, V. B. Yakovenko, and O. M. Dusmatov, Nonlinear Problems of the Dynamics of Vibration Protection Systems. Kaliningrad: Tekhnika, 1997, p. 204.

Search CrossRef
A. Kundu and S. Adhikari, “Transient response of structural dynamic systems with parametric uncertainty,” Journal of Engineering Mechanics, Vol. 140, No. 2, pp. 315–331, Feb. 2014, https://doi.org/10.1061/(asce)em.1943-7889.0000643

Publisher
N. S. Namachchivaya, “Random dynamical systems: addressing uncertainty, nonlinearity and predictability,” Meccanica, Vol. 51, No. 12, pp. 2975–2995, Nov. 2016, https://doi.org/10.1007/s11012-016-0570-4

Publisher
W. Sun, “Random vibration analysis on vertical vehicle-track coupled system with Timoshenko beam model,” Journal of Mechanical Engineering, Vol. 50, No. 18, p. 134, Jan. 2014, https://doi.org/10.3901/jme.2014.18.134

Publisher
Z. B. Bakirov, G. G. Tatkeeva, and S. K. Akhdiev, “Vibroprotection of transport vehicle operators,” Scientific Bulletin of NSTU, Vol. 55, No. 2, pp. 7–18, 2014.

Search CrossRef
M. A. Pavlovskii and L. M. Ryzhkov, “Random parametric oscillations of elastic systems with hysteresis energy dissipation,” International Applied Mechanics, Vol. 26, No. 9, pp. 890–895, Sep. 1990, https://doi.org/10.1007/bf00888776

Publisher
O. Dusmatov and M. U. Khodjabekov, “Problem of dynamics and stability of rod protected from vibrations in random parametric excitations,” International Journal of Research, Vol. 8, No. 12, Dec. 2021.

Search CrossRef
V. M. Kuz’Ma, “Dynamic instability of the random vibrations of a rod,” International Applied Mechanics, Vol. 2, No. 6, pp. 71–74, Jun. 1966, https://doi.org/10.1007/bf00887762

Publisher
A. Salvatore, B. Carboni, L.-Q. Chen, and W. Lacarbonara, “Experimental dynamic response of a nonlinear wire rope isolator,” Nonlinear Dynamics and Control, pp. 89–98, Jan. 2020, https://doi.org/10.1007/978-3-030-34747-5_9

Publisher
L. Chen, Z. Yuan, J. Qian, and J. Q. Sun, “Random vibration of hysteretic systems under Poisson white noise excitations,” Applied Mathematics and Mechanics, Vol. 44, No. 2, pp. 207–220, Jan. 2023, https://doi.org/10.1007/s10483-023-2941-6

Publisher
H. Zhang, Z. Wu, and Y. Xia, “Exponential stability of stochastic systems with hysteresis switching,” Automatica, Vol. 50, No. 2, pp. 599–606, Feb. 2014, https://doi.org/10.1016/j.automatica.2013.11.032

Publisher
L.-Y. Wang, Y.-G. Tang, Y. Li, J.-C. Zhang, and L.-Q. Liu, “Studies on stochastic parametric roll of ship with stochastic averaging method,” China Ocean Engineering, Vol. 34, No. 2, pp. 289–298, Apr. 2020, https://doi.org/10.1007/s13344-020-0027-3

Publisher
M. F. Younes, “Effect of different design parameters on damping capacity of liquid column vibration absorber,” Journal of Engineering and Applied Science, Vol. 65, No. 6, pp. 447–467, 2018.

Search CrossRef
M. Mirsaidov, O. Dusmatov, and M. Khodjabekov, “Mode shapes of transverse vibrations of rod protected from vibrations in kinematic excitations,” in Lecture Notes in Civil Engineering, Cham: Springer International Publishing, 2021, pp. 217–227, https://doi.org/10.1007/978-3-030-79983-0_20

Publisher
M. M. Mirsaidov, O. M. Dusmatov, and M. U. Khodjabekov, “Stability of nonlinear vibrations of plate protected from vibrations,” in Journal of Physics: Conference Series, Vol. 1921, No. 1, p. 012097, May 2021, https://doi.org/10.1088/1742-6596/1921/1/012097

Publisher
M. M. Mirsaidov, O. M. Dusmatov, and M. U. Khodjabekov, “Evaluation of the dynamics of elastic plate and liquid section dynamic absorber,” PNRPU Mechanics Bulletin, No. 3, pp. 51–59, Dec. 2022, https://doi.org/10.15593/perm.mech/2022.3.06

Publisher
A. Alifov, “Oscillations under a nonlinear parametric action and combinations of delays,” (in Russian), St. Petersburg State Polytechnical University Journal Physics and Mathematics, Vol. 17, No. 1, Jan. 2024, https://doi.org/10.18721/jpm.17105

Publisher
G. Malara, B. Pomaro, and P. D. Spanos, “Nonlinear stochastic vibration of a variable cross-section rod with a fractional derivative element,” International Journal of Non-Linear Mechanics, Vol. 135, p. 103770, Oct. 2021, https://doi.org/10.1016/j.ijnonlinmec.2021.103770

Publisher
M. L. Deng, W. Q. Zhu, and Q. F. Lü, “Stationary response of MDOF hysteretic system under random excitation,” International Journal of Non-Linear Mechanics, Vol. 170, p. 104994, Mar. 2025, https://doi.org/10.1016/j.ijnonlinmec.2024.104994

Publisher
F. Wang, X. Chen, and H. Xiang, “Parametric vibration model and response analysis of cable-beam coupling under random excitation,” Journal of Vibration Engineering and Technologies, Vol. 11, No. 5, pp. 2373–2386, Oct. 2022, https://doi.org/10.1007/s42417-022-00708-4

Publisher

About this article

Received

August 22, 2025

Accepted

October 28, 2025

Published

December 22, 2025

SUBJECTS

Vibration control, generation and harvesting

DOI

https://doi.org/10.21595/vp.2025.25300

Keywords

dynamic absorber

mechanical system

hysteresis

random parametric excitations

stochastic process

Acknowledgements

The authors have not disclosed any funding.

Data Availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Conflict of interest

The authors declare that they have no conflict of interest.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2019 03 31

Parameter optimization design of rotor dynamic vibration absorber

Zi Liang Liu, Qin Zhang, Yan Bo Cao, Qi Xu, Hong Liang Yao, Bang Chun Wen

Research article

2014 11 15

Response and performance of a nonlinear vibration isolator with high-static-low-dynamic-stiffness under shock excitations

Yong Wang, Shunming Li, Jiyong Li, Xingxing Jiang, Chun Cheng

Research article

2013 03 31

Nonlinear vibrations of beams with spring and damping delayed feedback control

Canchang Liu, Jinhao Qiu, Huiyu Sun, Zaihua Wang, Hongli Ji

O. Dusmatov, M. Khodjabekov, and B. Ashurov, “Random parametric nonlinear vibrations of a discrete mechanical system protected from vibration,” Vibroengineering Procedia, Vol. 60, pp. 44–53, Dec. 2025, https://doi.org/10.21595/vp.2025.25300

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2025.25300
UR  - https://doi.org/10.21595/vp.2025.25300
TI  - Random parametric nonlinear vibrations of a discrete mechanical system protected from vibration
T2  - Vibroengineering Procedia
AU  - Dusmatov, Olimjon
AU  - Khodjabekov, Muradjon
AU  - Ashurov, Bakhtiyor
PY  - 2025
DA  - 2025/12/22
PB  - Extrica
SP  - 44-53
VL  - 60
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

 @article{Dusmatov_2025, title={Random parametric nonlinear vibrations of a discrete mechanical system protected from vibration}, volume={60}, ISSN={2538-8479}, url={https://doi.org/10.21595/vp.2025.25300}, DOI={10.21595/vp.2025.25300}, journal={Vibroengineering Procedia}, publisher={JVE International Ltd.}, author={Dusmatov, Olimjon and Khodjabekov, Muradjon and Ashurov, Bakhtiyor}, year={2025}, month=dec, pages={44–53} }

Copy Bibtex

Copied to clipboard!

[1]O. Dusmatov, M. Khodjabekov, and B. Ashurov, “Random parametric nonlinear vibrations of a discrete mechanical system protected from vibration,” Vibroengineering Procedia, vol. 60, pp. 44–53, Dec. 2025, doi: 10.21595/vp.2025.25300.

Copy IEEE

Copied to clipboard!

Dusmatov, Olimjon, Muradjon Khodjabekov, and Bakhtiyor Ashurov. “Random Parametric Nonlinear Vibrations of a Discrete Mechanical System Protected from Vibration.” Vibroengineering Procedia 60 (December 22, 2025): 44–53. https://doi.org/10.21595/vp.2025.25300.

Copy Chicago

Copied to clipboard!

Random parametric nonlinear vibrations of a discrete mechanical system protected from vibration

Abstract

1. Introduction

2. Materials and methods

3. Result and discussion

4. Conclusions

References

About this article

Related Articles