Experimental study on vibration behavior of rotating manipulator in the process of scramming

1. Introduction

Manipulator is one of the most important and commonly used facilities in a variety of engineering applications. For example, the United States Robonaut, Ranger space manipulators can perform complex repair and assembly work on faulty satellites [1-2]. Because of the specificity of the space environment, vibration problem of space manipulator causes the task not being completed, and brings a great loss [3]. Therefore, the vibration behavior of manipulator has a very important effect on the manipulator’s work. Suppressing the vibration has been one of the significant problems to be solved urgently in the engineering field.

A huge amount of research efforts have been devoted to the vibration elimination of manipulator in the literature. Dickerson [4] and Alberts [5] use the passive vibration control method of pasting elasticity damping materials to inhibit the manipulator structural vibration. Book [8] adopts pole assignment technique to design the state feedback controller in order to reduce the vibration of the flexible robot response. Sakawa [6] uses the linear quadratic optimal control theory to define the state feedback gain, and suppress elastic deformation and vibration of flexible robot. Bailey [7] and Plump J. M. [8] completes groundbreaking experiments that organically combine passive vibration control and active vibration control with using piezoelectric materials.

There is not any work on the vibration behavior of manipulator during the rotating and scramming process. This paper presents an experimental study on the vibration behavior of rotating manipulator, and the manipulator’s vibration is restrained by pasting a damping layer. Through the experimental test, repeated impact phenomenon is found in the scramming process of manipulator. Via the feature extraction of repeated impact, the dynamics parameters of rotating manipulator are identified and an envelope model of the second impact response is established.

2. Experimental details and results

An aluminum tube with the length of 73 mm, the width of 25 mm, the height of 500 mm and the wall thickness of 1 mm is fixed on a rotating module, which acts as a rotating manipulator (Fig. 1). The measuring points and the direction of the manipulator’s rotation are shown in Fig. 1.

Fig. 1The manipulator

Three acceleration sensors are attached to the three points of the manipulator respectively. The manipulator is controlled under the rotational speed of five working conditions shown in Table 1. Under the five working conditions, the vibration behaviors of the three measuring points are tested.

According to the experimental test, the vibration behavior exists repeated impact phenomena. Repeated impact phenomenon is found in the scramming process of the manipulator (Fig. 2), including the first impact and the second impact.

Fig. 2The vibration behavior of the manipulator

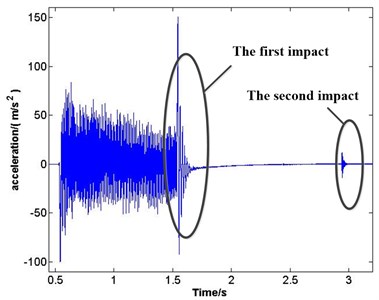
Fig. 2 is obtained from the vibration signal acquisition. The phenomenon of emerging repeated impact happens in the process of manipulator scramming, and the responses of repeated impact are free vibration.

3. The principle of envelope method for free vibration attenuation to identify dynamics parameters

Envelope method for free vibration attenuation is a commonly used method of measuring dynamics parameters [8]. Following the case of single degree of freedom, the principle of envelope method for free vibration attenuation to identify dynamics parameters is explained.

Attenuation response for a damping system of single degree of degree can be expressed as:

where $C$ is amplitude, ${\omega }_n$ is natural frequency, $t$ is time of free vibration, $\phi$ is phase difference angle and $\varsigma$ is damping ratio of the system. According to Eq. (1), envelope curve equation for displacement attenuation of single-degree-of-freedom vibration is Eq. (2):

Eq. (1) is displacement response, because of different types of vibration picking sensors, time-domain signal of attenuation response of velocity or acceleration may be obtained. Equations of velocity and acceleration are shown as Eq. (3) and Eq. (4):

where $B$ and $A$ are amplitudes of velocity and acceleration attenuation response respectively. And $\theta$ and $\beta$ are the phase difference angles of velocity and acceleration attenuation response respectively. Eq. (4) and Eq. (1) have the same type, so acceleration response curve of single-degree-of-freedom vibration have the same envelope curve with displacement response, and the response curve is shown in Fig. 3.

Fig. 3Time domain response curve of single degree freedom system

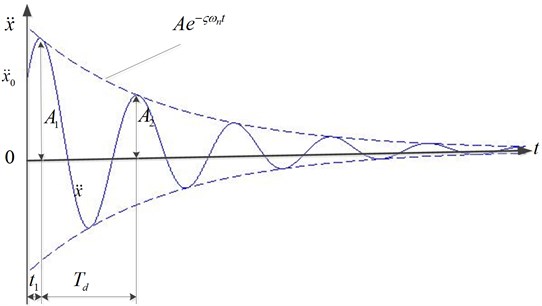
In Fig. 3, damping makes the amplitude of system vibration decrease by geometric attenuation. The ratio of two adjacent amplitude is shown in Eq. (5):

where $A_1$, $A_2$ are the values of two adjacent amplitude, $t_1$ is the time of the first amplitude, $\eta$ is called damping coefficient [9] and $T_d$ is vibration period:

Based on Eq. (6), amplitude reduces to the initial value $1/e^{\varsigma {\omega }_n{T}_d}$ multiple every vibration period. In fact, in order to avoid inconvenience of taking the index value. Common logarithm damping $\delta$ replaces damping coefficient $\eta$ shown in Eq. (7):

According to Eq. (6) and Eq. (7), equations of damping ratios and natural frequency is shown as follows:

4. Experimental analysis

4.1. Dynamic parameters recognition of the manipulator

Due to the influence of noise, de-noising method [11] is used to the first impact response of measuring point 1 on condition 1. The first impact response after de-noising processing is shown in Fig. 4, and $x$-axis represents time and $y$-axis represents acceleration value.

Fig. 4The first impact after de-noising processing

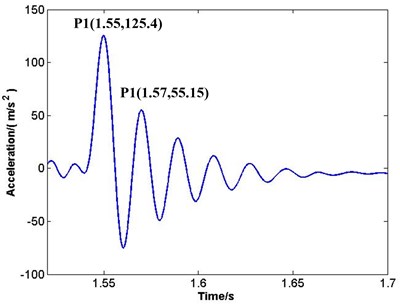
P1, P2 in vibration waveform (Fig. 4) are the first and the second peak points, and coordinate values of the two peaks are P1(1.55, 125.4), P2(1.57, 55.15). That means $A_1=\text{125.4}{\text{m/s}}^{\text{2}}$ and $A_2=\text{55.15}{\text{m/s}}^{\text{2}}\text{.}$ Under other conditions, $A_1$ and $A_2$ can be obtained by the same analysis (Table 2).

Table 2Peak points’ value of A1 and A2 (m/s2)

	Measuring point 1		Measuring point 2		Measuring point 3
	$A_1$	$A_2$	$A_1$	$A_2$	$A_1$	$A_2$
Condition 1	125.4	55.15	72.46	30.53	26.15	9.11
Condition 2	45.19	18.74	26.37	9.35	8.92	2.44
Condition 3	17.34	8.39	11.24	4.18	5.17	1.17
Condition 4	14.64	4.73	8.76	2.57	0.74	0.2
Condition 5	14.77	5.50	8.52	2.98	3.04	0.97

According to the data of Table 2, Eqs. (7)-(9), damping ratios (Table 2) and natural frequencies (Table 3) can be obtained in different measuring points of different conditions.

Table 3Damping ratios

	Measuring point 1	Measuring point 2	Measuring point 3
Condition 1	0.131	0.149	0.164
Condition 2	0.156	0.163	0.203
Condition 3	0.174	0.182	0.223
Condition 4	0.181	0.192	0.228
Condition 5	0.162	0.169	0.183

Table 4Natural frequencies (Hz)

	Measuring point 1	Measuring point 2	Measuring point 3
Condition 1	52.82	50.56	50.68
Condition 2	50.62	50.68	51.06
Condition 3	50.77	50.85	48.85
Condition 4	50.84	50.95	51.35
Condition 5	48.26	53.39	53.53

The average of damping ratios in Table 3 and natural frequencies in Table 4 are 0.177 and 50.86 Hz respectively. Therefore, $\varsigma =\text{0.177}$ and ${\omega }_n=\text{50.86}\text{Hz}$ can evaluate the damping ratio and the natural frequency.

4.2. Hammer experiment

Using hammer experiment [12] verifies the natural frequency (Fig. 5).

Fig. 5Hammer experiment

Natural frequencies got from hammer experiment are shown in Table 5.

Table 5Natural frequencies obtained by hammer experiment (Hz)

	First-order	Second-order	Third-order	Fourth-order	Fifth-order
Natural frequencies	52.61	308.41	350.40	429.31	609.18

According to Table 5, first-order natural frequency got from hammer experiment is 52.61 Hz, which is very close to the natural frequency 50.86 Hz got from the first impact of the manipulator (the error is 3.33 %), and proves the value of natural frequency 50.86 Hz is correct.

4.3. Establishing an envelope model of the second impact response

According to these dynamics parameters got from the first impact, an envelope model of the second impact response is established as follows:

10

$x=\pm A{e}^{-2{\pi \varsigma \omega }_n(t-t_0)},$

where $x$ is the acceleration of vibration, $A$ is the initial acceleration value of the second impact; $t$ is multivariate time and $t_0$ is the initial time. Besides, $\varsigma$ is 0.177 and ${\omega }_n$ is 50.86 Hz.

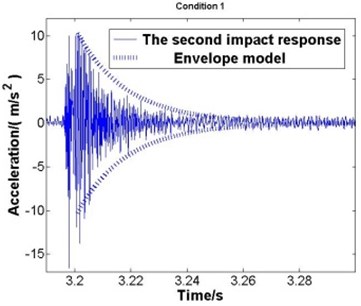
The envelope model is verified by experiment. Fig. 6(a)-(e) respectively represent the second impact response of condition 1 to condition 5.

Fig. 6The second impact and the envelope model

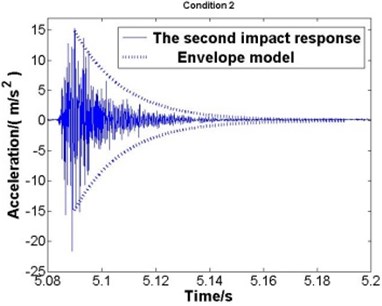
a) Condition 1

b) Condition 2

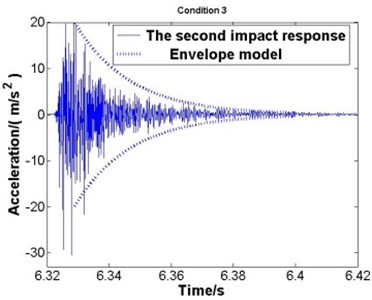
c) Condition 3

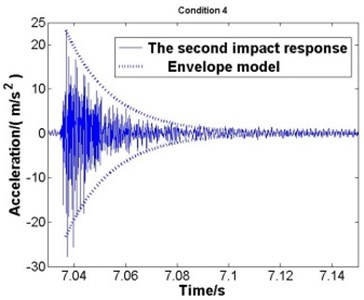
d) Condition 4

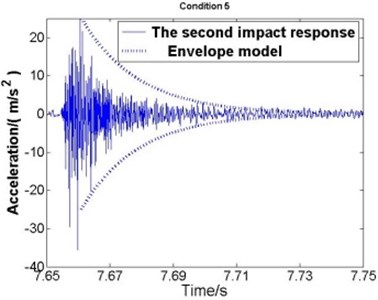
e) Condition 5

Where the solid line represents the second impact response and the dotted line represents the envelope model. According to the comparisons, good agreement is observed, which proves that the dynamics parameters got from the first impact is correct and the envelope model is applicable.

5. Adding a damping layer to restrain the vibration of manipulator

A sharp spike of acceleration arises in the first impact (Fig. 7). In order to restrain the vibration, a damping layer is added to the surface of the manipulator [13] (Fig. 8). The manipulator is controlled at the rotational speed on five working conditions as shown in Table 1 to do the experimental test.

Fig. 7Existing a sharp spike

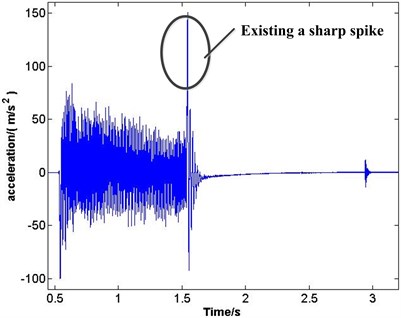
Fig. 8The manipulator with a damping layer

The sharp spikes of manipulator with a damping layer and without a damping layer are compared in different measuring points under different conditions (as shown in Fig. 9). $X$-axis represents rotational speed and $y$-axis represents acceleration value.

Fig. 9Comparing the sharp spikes

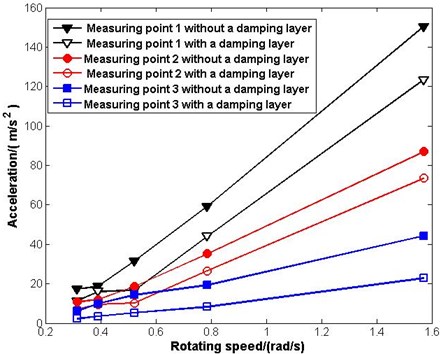
Where the first black line represent the sharp spikes of measuring point 1 without a damping layer in different rotating speed, the second black line represents measuring point 1 with a damping layer and the two lines make a comparison. Similarly, the two red lines make the comparison of measuring point 2 without a damping layer and with a damping layer and the two blue lines make the comparison of measuring point 3. Therefore, a conclusion can be obtained that adding a damping layer can suppress the vibration of the manipulator through the above comparisons.

6. Conclusions

Experimental study on the vibration behavior of a rotating manipulator during rotating and scamming process has been made. Repeated impact phenomenon is found in the scramming process of the manipulator. Conclusions obtained are as follow: (1) Dynamics parameters of the rotating manipulator are identified by the feature extraction of the first impact; (2) Using hammer experiment verifies the natural frequency correct; (3) Based on these dynamics parameters, an envelope model of the second impact response is established, and the applicability of the model is validated by experiments; (4) A sharp spike of acceleration arises in the first impact. A damping layer added to the surface of the manipulator is used to suppress the vibration, and via the experimental verification, the damping layer takes a certain effect on the vibration elimination.