Two-dimensional approximately harmonic projection for gait recognition

1. Introduction

Recently, the average silhouettes-based human gait recognition has received extensive attention due to its potential applications in many fields [1-4], such as identity authentication and video surveillance. In general, a binary silhouette image of size 128×88 in the USF HumanID gait database is represented as a vector in the image space ${\mathbb{R}}^{\text{128×88}}$. Consequently, a major challenge of gait recognition is that the captured gait image often lies in a high-dimensional image space. Due to the consideration of the curse of dimensionality, a common way to resolve this problem is to use dimensionality reduction techniques. Once we obtain lower-dimensional representations of the original gait images, the traditional classification methods can be applied in the reduced feature space. Therefore, the main objective of this paper is to find techniques that can introduce lower-dimensional feature representations of gait images with enhanced discriminatory power.

The most representative algorithms for dimensionality reduction are principal component analysis (PCA) and linear discriminant analysis (LDA) [5]. Although PCA and LDA have been successfully applied to face recognition, image retrieval, and gait recognition, they are designed for discovering only the global Euclidean structure, whereas the local manifold structure is ignored. In fact, the global statistics such as variance is often difficult to compute when there are no sufficient samples. In addition, a number of research efforts have shown that the images possibly reside on a nonlinear submanifold and the representation of image is fundamentally related to the problem of manifold learning [6-9]. Given a set of high-dimensional data points, manifold learning techniques aim to discover the geometric properties of the data space. In the past years, a number of manifold learning algorithms have been developed, representative algorithms include locally linear embedding (LLE) [10], ISOMAP [11], and Laplacian eigenmaps (LE) [12]. LLE is designed to maintain the local linear reconstruction relationship among neighboring points in the lower-dimensional space. ISOMAP aims to preserve global geodesic distances of all pairs of samples. LE aims to preserve proximity relationships by manipulations on an undirected weighted graph, which indicates neighbor relations of pairwise samples. These nonlinear methods do yield impressive results on some artificial benchmarks and several real applications. However, they suffer from the out of sample problem, i.e., they can only obtain mappings that are defined on the training data points and how to explicitly calculate the mappings on novel testing data points remains unclear. Therefore, these nonlinear manifold learning algorithms might not be suitable for gait recognition. To cope with the out of sample problem, locality preserving projection (LPP) [13] applies a linearization procedure to construct explicit mappings over new samples. In the recent research, Lin et al. [14] point that utilizing the affine hulls of the manifold and the connected components is more effective for preserving the local geometrical structure and cluster structure of original data, and propose a new algorithm termed approximately harmonic projection (AHP) for dimensionality reduction. AHP is a linear manifold learning method based on the harmonic framework, and the optimal transformation can be obtained by approximating the Dirichlet integral. It is worth noting that all these methods unfold input data into vectors before dimensionality reduction. But images are naturally in the form of second-order or higher-order tensors [15-17]. For example, gray-level images represent second-order (matrix), and Gabor-filtered image represents third-order tensors. Consequently, such kind of vectorization largely increases the computational costs and seriously destroys the intrinsic tensor structure of images. To cope with these issues, multilinear extensions of PCA, LDA, and LPP, namely 2DPCA [18], 2DLDA [19], and 2DLPP [20] are proposed, respectively. These methods aim to conduct subspace analysis by directly encoding images as two-dimensional image matrices rather than one-dimensional vectors. The advantages of using image-as-matrix representation have been indeed consistently pointed out in a number of recent research efforts [15-20], especially when the number of training samples is small. Nevertheless, the multilinear (tensor) extension of AHP and its application to gait recognition are still a research area where few people have tried to explore.

This paper represents a gray-level average silhouette image of size $n_1\times n_2$ as the matrix (or second-order tensor) in the tensor space ${\mathbb{R}}^{n_1}\times {\mathbb{R}}^{n_2}$. Then a two-dimensional approximately harmonic projection (2DAHP) is proposed by tensorizing AHP. Compared with the original AHP, 2DAHP can directly process gait images in their original matrix form and utilize correlations among pixels within different dimensions (i.e., rows and columns). Moreover, the smaller number of data entries along each data dimension facilitates subspace learning with limited training data. 2DAHP is much more computational efficient since the decomposed matrices are of size $n_1\times n_1$ or $n_2\times n_2$, which is much smaller than that of size $n\times n(n=n_1\times n_2)$ in AHP. 2DAHP can avoid the singularity problem. In addition, the trace ratio optimization technique is also applied to efficiently solve 2DAHP.

The remainder of this paper is organized as follows. Section 2 briefly reviews AHP. Section 3 introduces our proposed 2DAHP algorithm. Experimental results on gait recognition are presented in Section 4. The concluding remarks are provided in Section 5.

2. Brief review of approximately harmonic projection (AHP)

AHP is a recently proposed linear manifold learning method for dimensionality reduction [14]. It is based on the approximate affine hull and explicitly utilizes the edge length to reflect the geometrical structure of the manifold structure of the data space.

Given a set of data points $\{x_1,\cdots ,x_n\}\subset {\mathbb{R}}^m$, let $X=[x_1,\cdots ,x_n]$. Let $W^c$ and $W^b$ be two weight matrices defined on the data points. The optimal projection of AHP can be obtained by solving the following minimization problem:

with the constraint:

where $e_{ij}=x_j-x_i$ represents an edge vector that has an orientation from $x_i$ to $x_j,$$d_{ij}=\Vert x_j-x_i\Vert$ denotes the length of the edge between $x_i$ and $x_j$, $t$ is the arc length of $e_{ij}$. $W^c$ and $W^b$ are two matrices defined as follows: if $x_i$ and $x_j$ are connected, then $W_{ij}^c=1/d_{ij}$ and $W_{ij}^b=d_{ij};$ otherwise, $W_{ij}^c=W_{ij}^b=0.$$D^c$and $D^b$ are two diagonal matrices defined as $D_{ii}^c={\sum }_j{W}_{ij}^c$, $D_{ii}^b={\sum }_j{W}_{ij}^b$. $\nabla f_{e_{ij}}$ denotes the gradient on each edge, its definition is as follows:

Unlike the standard spectral graph methods which mainly consider the connectivity of graph, AHP explicitly makes use of the edge length and edge orientation which reflect the geometrical structure of the manifold. Therefore, AHP can precisely model multiple connected components of the data manifold, which is especially important for discriminating data with different submanifold (cluster) structure.

The objective function in AHP aims to use the approximate affine hull of the graph to separate data points sampled from different components. Therefore, minimizing it is to ensure that if $x_i$ and $x_j$ lie in the multiple connected components, then $y_i(=a^T{x}_i)$ and $y_j(=a^T{x}_j)$ are made close by the optimal projection. Finally, the projection vector $a$ that minimizes (1) is given by the minimum eigenvalue solution to the generalized eigenvalue problem:

Note that, in the appearance-based image analysis, one is often confronted with the fact the dimension of image vector is much smaller than the number of images. Thus, the matrix $X(2D^b+W^b)X^T$ is singular. To avoid the singularity problem, one may first apply PCA to remove the components corresponding to zero eigenvalues. Thus, the projection vector of AHP can be considered as the eigenvectors of the matrix ${\left(X\right(2D^b+W^b\left)X^T\right)}^{-1}X(D^c-W^c)X^T$ associated with the smallest eigenvalues. In addition, since ${\left(X\right(2D^b+W^b\left)X^T\right)}^{-1}X(D^c-W^c)X^T$ is not usually symmetric, the AHP projection axes are not orthogonal.

Let the column vector of $a_1,a_2,\cdots ,a_d$ be the solution of (4) ordered according to their eigenvalues ${\lambda }_1<{\lambda }_2<\cdots <{\lambda }_d$. Thus, the embedding is given by $x_i\to y_i=A^T{x}_i$, where $y_i$ is a $d$-dimensional vector and $A=(a_1,a_2,\cdots ,a_d)$ is an $n\times d$ matrix.

3. Two-dimensional approximately harmonic projection (2DAHP)

Given a set of data points ${\left\{X_i\right\}}_{i=1}^n$ in the second-order tensor (or matrix) space ${\mathbb{R}}^{n_1}\otimes {\mathbb{R}}^{n_2}$, let ${\left\{u_i\right\}}_{i=1}^{n_1}$ be an orthonormal basis of ${\mathbb{R}}^{n_1}$ and ${\left\{v_j\right\}}_{j=1}^{n_2}$ be an orthonormal basis of ${\mathbb{R}}^{n_2}$, it has been shown that $\{u_i\otimes v_j\}$ forms a basis of the tensor space ${\mathbb{R}}^{n_1}\otimes {\mathbb{R}}^{n_2}$ [20]. Thus, a second-order tensor $X$ can be uniquely defined as $X=\sum _{i,j}\left(u_i^{T}X{v}_j\right)u_i{v}_j^T$.

Given a set of data points ${\left\{X_i\right\}}_{i=1}^n$ in ${\mathbb{R}}^{n_1}\otimes {\mathbb{R}}^{n_2}$, two-dimensional approximately harmonic projection (2DAHP) aims to find two projection matrices $U\in {\mathbb{R}}^{n_1\times l_1}$ and $V\in {\mathbb{R}}^{n_2\times l_2}$ that maps each data point $X_i\left(i=1,\cdots ,n\right)$ to a lower-dimensional matrix representation $Y_i\in {\mathbb{R}}^{l_1}\times {\mathbb{R}}^{l_2}(i=1,\cdots n,l_1<n_1,l_2<n_2)$ by $Y_i=U^T{X}_{i}V$ such that $Y_i$ represents $X_i$.

Let $U$ and $V$ be the projection matrices, according to (1) and (2), the optimal objective function of 2DAHP with the matrix representation can be rewritten as follows:

with the constraint:

where $d_{ij}$ is similarly defined as AHP.

Let $Y_i=U^T{X}_{i}V$ and $D^c$ be a diagonal matrix, $D_{ii}^c={\sum }_j{W}_{ij}^c$. Since ${\Vert A\Vert }^2=\text{Tr}\left(A{A}^T\right)$, we have:

where $P_V^c=\sum _i{D}_{ii}^c{X}_{i}V{V}^T{X}_i^T$ and $Q_V^c=\sum _{i,j}{W}_{ij}^c{X}_{i}V{V}^T{X}_j^T$. Similarly, ${\Vert A\Vert }^2=\text{Tr}\left(A^{T}A\right)$, so we can also obtain:

where $P_U^c=\sum _i{D}_{ii}^c{X}_i^{T}U{U}^T{X}_i$ and $Q_U^c=\sum _{i,j}{W}_{ij}^c{X}_i^{T}U{U}^T{X}_j.$ Consequently, we should simultaneously minimize $\text{Tr}\left(U^T\right(P_V^c-Q_V^c\left)U\right)$ and $\text{Tr}\left(V^T\right(P_U^c-Q_U^c\left)V\right)$.

In addition, similar to the above derivation process, the left side of constraint function equation (6) can be converted to:

where $P_V^b=\sum _i{D}_{ij}^b{X}_{i}V{V}^T{X}_i^T$, $Q_V^b=\sum _i{W}_{ij}^b{X}_{i}V{V}^T{X}_j^T$, $P_U^b=\sum _i{D}_{ij}^b{X}_i^{T}U{U}^T{X}_i$, $Q_U^b=\sum _i{W}_{ij}^b{X}_i^{T}U{U}^T{X}_j,$ and $D^b$ is a diagonal matrix, $D_{ii}^b={\sum }_j{W}_{ij}^b$.

Finally, the optimal objective function (5) subject to (6) can be transformed as:

Because of difficulty in solving the optimal $U$ and $V$ simultaneously, we follows the similar computational methods as [20] to compute $U$ and $V$ iteratively. We first initialize $U$ with an identity matrix, then $V$ can be approximately computed with generalized eigenvalue decomposition (GED) by transforming the optimal objective function (11) into the tractable ratio trace form $\text{Tr}\left({\left(V^T\right(2P_U^b+Q_U^b\left)V\right)}^{-1}\right(V^T(P_U^c-Q_U^c)V\left)\right)$. That is, $V$ can be regarded as the eigenvectors associated with the minimum eigenvalues of the following generalized eigenvector problem:

Once $V$ is obtained, similarly, we can update $U$ by solving the following generalized eigenvector problem:

Therefore, we can obtain the final optimal $U$ and $V$ by iteratively solving the generalized eigenvector problems (12) and (13).

In the preceding section, we approximately computed the the optimal objective functions of (10) and (11) by converting them into ratio trace problems, which are solved by GED. However, the obtained solutions may deviate from the original objectives, which may lead to uncertainty in subsequent classification [21]. To address these problems, we describes how to directly solve (10) and (11) with the Iterative algorithm for the Trace Ratio (ITR) optimization problem introduced in [21]. To compute $U$, we first fix $V$ and initialize $U^0$ as an arbitrary columnly orthogonal matrix. In each iterative step, we solve a trace difference problem $U^t=\mathrm{a}\mathrm{r}\mathrm{g}\underset{U^{T}U=I}{\mathrm{m}\mathrm{i}\mathrm{n}}\text{Tr}\left(U^T\right((P_V^c-Q_V^c)-{\lambda }^t(2P_V^b+Q_V^b)\left)U\right)$, where ${\lambda }^t$ is the trace ratio value calculated from the projection matrix $U^{t-1}$ of the previous step, i.e., ${\lambda }^t=\text{Tr}\left(U^{t-1^T}\right(P_V^c-Q_V^c\left)U^{t-1}\right)/\text{Tr}\left(U^{t-1^T}\right(2P_V^b+Q_V^b\left)U^{t-1}\right)$. Once $U$ is obtained, similarly, we can update $V$ by solving $V^t=\mathrm{a}\mathrm{r}\mathrm{g}\underset{V^{T}V=I}{\mathrm{m}\mathrm{i}\mathrm{n}}\text{Tr}\left(V^T\right((P_U^c-Q_U^c)-{\lambda }^t(2P_U^b+Q_U^b)\left)V\right)$ where ${\lambda }^t=\text{Tr}\left(V^{t-1^T}\right(P_U^c-Q_U^c\left)V^{t-1}\right)/\text{Tr}\left(V^{t-1^T}\right(2P_U^b+Q_U^b\left)V^{t-1}\right)$. Finally, output the final $U$ and $V$ when the iterative algorithm converges to optimal solutions. The detailed iteration algorithm for solving (10) and (11) can be presented as follows:

Algorithm1: The iteration algorithm for directly solving the optimal problem (10) and (11) in 2DAHP.

Step 1: Initialize $U^0$ and $V^0$ as two arbitrary column-wise orthogonal matrices.

Step 2: For $t=\mathrm{1,2},\cdots T_{\mathrm{m}\mathrm{a}\mathrm{x}}$, do

Step 2.1: Calculate the trace ratio value ${\lambda }^t$ according to the projection matrix $U^{t-1}$:

Step 2.2: Obtain the new $U^t$ by solving the following eigen-decomposition problem:

Step 2.3: For the given $U^t$, calculate the trace ratio value ${\lambda }^t$ according to the projection matrix $V^{t-1}$:

Step 2.4: Obtain the new $V^t$ by solving the following eigen-decomposition problem:

where ${\tau }_0^t\le {\tau }_1^t\le \cdots \le {\tau }_{d-1}^t$ are the $d$ smallest eigenvalues, and $V_i^t$ is the eigenvector associated with eigenvalue ${\tau }_i^t$, which constitutes the ith column vector of the matrix $V^t$.

Step 2.5: If $\Vert U^t-U^{t-1}\Vert <\sqrt{d}\epsilon$ and $\Vert V^t-V^{t-1}\Vert <\sqrt{d}\epsilon$, then break.

Step 3: Output the projection matrices $U=U^t$ and $V=V^t$.

From the above algorithemic procedure, it can be easily observe that the obtained projection matrices $U$ and $V$ are orthogonal. In addition, following the conclusions in [21], the above iteration algorithm will converge to an optimal value. For more details about proof of convergence, please refer to [21].

4. Experimental results

In this section, to investigate the performance of our proposed 2DAHP algorithm for gait recognition, we compare the 2DAHP algorithm with 2DPCA [18], 2DLDA [19], 2DLPP [20], and the original AHP [14] algorithms for gait recognition on the well-known USF HumanID gait database, where 2DPCA, 2DLDA, and 2DLPP are three popular tensor methods in face recognition and gait recognition, and the original AHP algorithm is a vector-based algorithm. The settings of these compared algorithms are identical to the description in the corresponding papers. In addition, to cope with the singular problem existed in the original AHP, we apply PCA to remove the components corresponding to zero eigenvalues before carrying out AHP. For 2DAHP, we empirically set the optimal iteration number $T_{\mathrm{m}\mathrm{a}\mathrm{x}}$ as 5 for each probe set, since the latter experimental results show that the 2DAHP algorithm converges quite quickly.

The USF HumanID gait database is constructed by Sarkar et al. [1], it contains 1870 sequences from 122 individuals walking on an elliptical path in front of two cameras. This database provided one gallery set containing the sequences from 122 individuals and 12 probe sets containing different numbers of individuals varying from 33 to 122 for algorithm training and testing, respectively. More details information about the USF HumanID gait database can be found in [1]. In this gait database, we consider sequences of binary silhouette images. As in [22] and [23], we construct the average silhouette-based gait image representation: First, a complete sequence is partitioned into several subsequences according to the gait period length $N_{gait}$ provided by Sarkar et al. [1]. Then, the binary silhouette images within each gait cycle of a sequence are averaged to acquire several gray-level average silhouette images according to:

where $\left\{T\right(1),\cdots ,T(F\left)\right\}$ represents the binary images for one sequence with $F$ frames, $\lfloor F/N_{gait}\rfloor$ denotes the largest integer less than or equal to $F/N_{gait}$. Since numerous researches have experimentally shown that the average silhouette image is more effective and efficient than the original binary silhouette image for human gait recognition, we also utilize the average silhouette image for gait recognition. Fig. 1 shows some original binary images and the average silhouette images of two different individuals, where the first seven images and the last image in each row denote the binary silhouette images and the average silhouette images, respectively. As can be seen, different individuals have different average silhouette images.

To perform gait recognition, we first obtain the average silhouette image subspaces by dimensionality reduction algorithms. Then, all the averaged images from both the gallery set and probe sets are projected into the image subspaces. Finally, the nearest-neighbor classifier is adopted to identify new average silhouette images, where the distance measure uses the median operator for its robust to noise [1, 23]:

where $L{S}_P\left(i\right)$, $i=1,\cdots ,N_p$ and $L{S}_G\left(j\right)$, $j=1,\cdots ,N_g$ are the lower representations from one probe sequence and one gallery sequence, respectively, $N_p$ and $N_g$ denote the total number of average silhouette images. For each dimensionality reduction algorithm, we only show its performance in the $l-$ or $(l\times l)-$ dimensional subspace. For each case, we average the results over 20 random splits of training and testing sets.

Fig. 1Some original binary images and the average silhouette images of two different individuals in the USF HumanID gait database

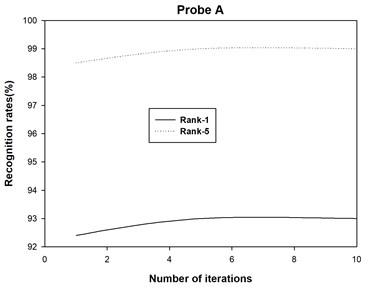
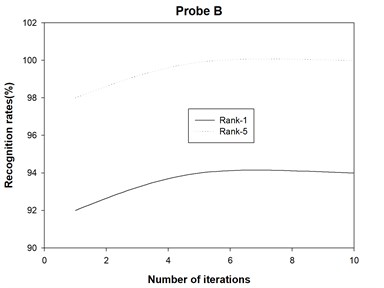
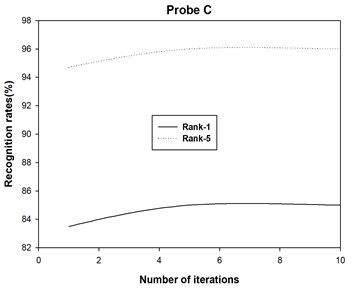
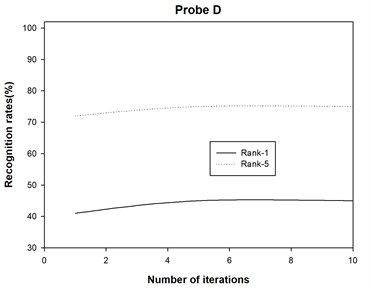
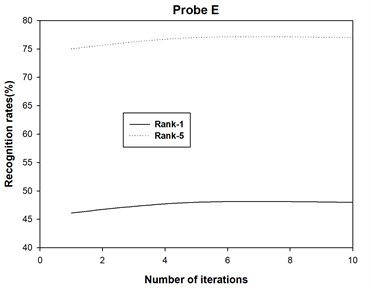
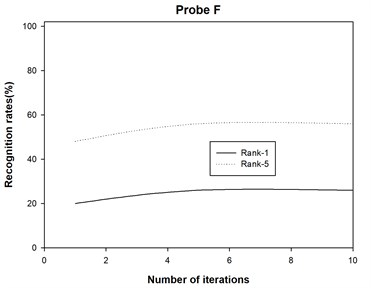
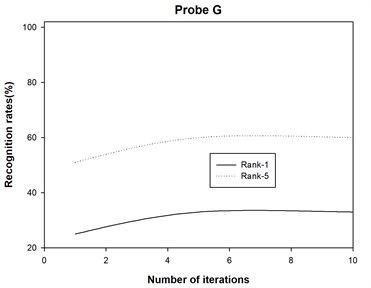
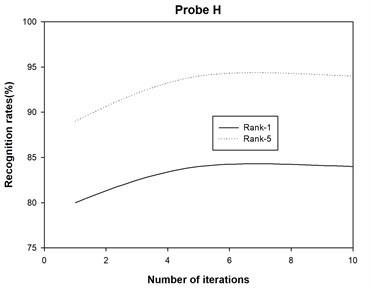
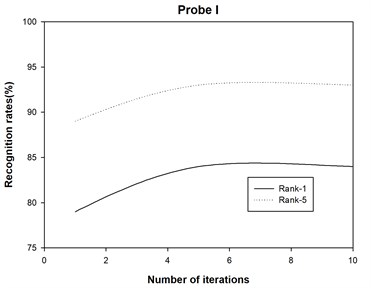
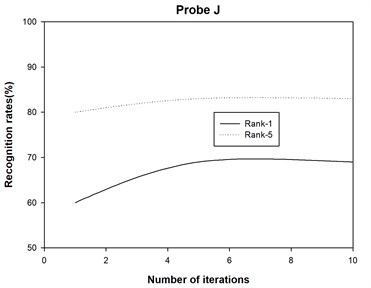
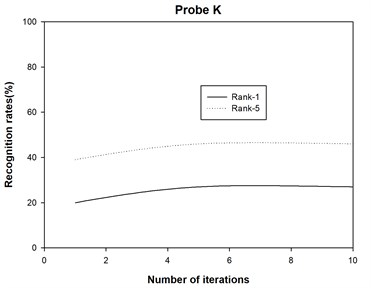
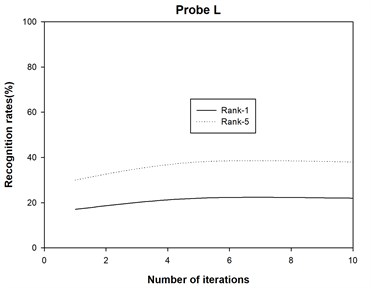
The recognition accuracies are shown in Table 1 and Table 2, where Rank-1 indicates that the correct subject is ranked as the top candidate, Rank-5 means that the correct subject is ranked among the top five candidates, and Average denotes the recognition rate among all the probe sets. Moreover, we also plot the recognition rate variance with different numbers of iterations for probe sets A, B, C, D, E, F, G, H, I, J, K and L in Fig. 2. Finally, we report the running times of 2DAHP and AHP in Table 3.

From the experimental results listed in Table 1-3 and Fig. 2, we can have the following observations:

1) Our proposed 2DAHP consistently outperforms the 2DPCA, 2DLDA, 2DLPP, and AHP algorithms, which demonstrates that it is beneficial to use simultaneously two-dimensional matrix representation as well as the local geometrical structure and cluster structure for gait recognition.

2) 2DPCA performs the worst among the compared algorithms. A possible explanation is as follows: similar to the traditional PCA, the 2DPCA is simply achieves object reconstruction and it is not necessarily useful for discriminating gait images with different subjects which is the ultimate goal of gait recognition.

3) The 2DLDA performs comparatively to 2DLPP. This demonstrates that it is hard to evaluate whether local manifold structure or class label information is more important, which is consistent with existing studies.

4) The 2DAHP algorithm converges quite quickly for probe sets A, B, C, D, E, F, G, H, I, J, K and L, and recognition rates changes slightly with different iteration numbers. After about 5 iterations, 2DAHP can converge to the optimal solution in all 12 probe sets.

5) 2DAHP achieves significant speed up comparing to AHP. Theses results are consistent with the theoretical analysis of the efficiency, i.e., 2DAHP can utilize the intrinsic tensor structure of gait images to improve running efficiency.

Fig. 2Some original binary images and the average silhouette images of two different individuals in the USF HumanID gait database

a)

b)

c)

d)

e)

f)

g)

h)

i)

j)

k)

l)

5. Conclusions

This paper introduces a tensor dimensionality reduction algorithm called two-dimensional approximately harmonic projection (2DAHP). Compared with the original AHP, 2DAHP can directly conducts subspace analysis by encoding an image as a two-dimensional matrix and has higher computational efficiency. Experimental results on gait recognition have demonstrated the effectiveness and efficiency of our proposed approach.