Incipient fault diagnosis of roller bearings using empirical mode decomposition and correlation coefficient

1. Introduction

Roller bearings are one of the most important and commonly used components in the rotating machines. Bearing failure is a common cause of the breakdown of machines. In order to maintain a low machinery downtime, the incipient fault detection and identification of roller bearings are crucial. Different methods for roller bearing fault diagnosis, such as vibration and acoustic measurements, temperature measurements and wear debris analysis [1], have been investigated recently. Among these, vibration measurement and analysis are the most extensively employed in the condition monitoring and fault recognition of the rotating machinery [2-4].

However, it is difficult to diagnose the faults in early stages of the bearing failure, because vibrations generated by the faults have low amplitude and can be easily masked by noise. A signal processing technique called envelope analysis is useful to overcome this problem. When faults occur in the roller bearing, the vibration signals present the feature of modulation that combines the characteristic frequency of the bearing fault with various machine natural frequencies excited by impacts, which are produced when a running roller passes over the surfaces of the defects. Therefore demodulation or enveloping based methods have been established and widely used for roller bearing fault diagnosis [5-7]. However, the central frequency and bandwidth of a band-pass filter needs to be selected with experience before forming the envelope signal in conventional envelope analysis method, which yields subjective influences on the accuracy of the analysis results [8, 9]. A new time-frequency analysis method called empirical mode decomposition (EMD) was developed by Huang et al. [10] in recent years and has been successfully applied to fault diagnosis of roller bearings by many researchers [11, 12]. The EMD method is based on the local time scale of a signal and decomposes the complicated signal into a number of intrinsic mode functions (IMF). Each IMF component involves the local characteristic of the signal and the spectral band for each IMF ranges from high to low frequency and changes with the signal itself. Therefore EMD is a powerful method for processing non-linear and non-stationary signals and can be considered as a self-adaptive filter whose central frequency and bandwidth change with the signal itself.

In this work, a new method combining EMD and correlation coefficient is proposed for detection and identification of bearing faults at an early stage. The fundamental step of the novel method is the incipient bearing fault detection. The idea is motivated by the novelty in detection philosophy. Differently, the proposed method is based not on pattern recognition but on EMD and correlation coefficient. The novelty detection [13, 14] has been proposed in order to overcome the limitation of pattern recognition, which is that the fault pattern classification is based on the assumption that the distribution of available data between classes is relatively balanced [15-17]. As it is known, in practical applications it is almost impossible to obtain data for faulty types of bearings, because data describing fault conditions is often non-existent and acquiring it would require damaging the bearing in purpose. So this method, similar to novelty detection, eliminates the need for collecting failure data in advance. Subsequently, together with the fault detection, an envelope analysis of IMFs of faulty signals, which are self-adaptively decomposed by means of EMD, is presented to identify the location of the defects.

2. Empirical mode decomposition

The EMD method is proposed to process the nonlinear and non-stationary data by decomposing the data into a sequence of amplitude-modulation or frequency-modulation components or alike. These components to be obtained are called IMFs, each of which must satisfy the two conditions [10]: (1) in the whole data set, the number of extrema and the number of zero-crossings must either equal or differ at most by one; and (2) at any point, the mean of the envelope defined by local maxima and the envelope defined by the local minima are zero.

The EMD procedures of any signal $x\left(t\right)$ can be described as follows [10]:

(1) Find out all the local extrema, and then connect all the local maxima by a cubic spline line as the upper envelope.

(2) Repeat the procedure (1) for the local minima to produce the lower envelope.

(3) Compute the mean of upper and lower envelope, $m_1$. The difference between the original signal $x\left(t\right)$ and $m_1$ is the first component, designated as $h_1$, i.e.:

If $h_1$ is an IMF, $h_1$ is designated as $c_1$.

(1) If $h_1$ does not satisfy the condition of IMF, $h_1$ is treated as the original signal and steps (1)-(3) are repeated until the result becomes an IMF.

(2) Subtract $h_1$ from $x\left(t\right)$, we could get:

Then $r_1$ is treated as the original data and repeating the above processes, the second IMF $c_2$ of $x\left(t\right)$ could be obtained. Repeat all the steps mentioned above for $n$ times resulting in $n$ IMFs of signal $x\left(t\right)$.

The decomposition will stop as soon as $r_n$ becomes a monotonic function from which no more IMFs can be extracted. Finally, the original signal $x\left(t\right)$ can be represented as:

Residue $r_n$ represents the mean trend of $x\left(t\right)$, and the IMFs $c_1$, $c_2$, …, $c_n$ include different frequency bands from high to low.

3. Correlation coefficient

For the given signals $x\left(n\right)$ and $y\left(n\right)$, the correlation coefficient is defined as [18]:

where ${\rho }_{xy}$ is the normalized value of the cross-correlation function at the zero-lag point, which is different from the commonly used Pearson’s correlation coefficient.

4. Roller bearing fault diagnosis method based on EMD and correlation coefficient

While there is a fault in the roller bearings, the spectrum will change in a determined way [19]. The high frequency resonance phenomena begin to emerge as the bearing defects form gradually at an incipient stage. Therefore the high frequency content is sensitive to the change of the bearing conditions. Accordingly, the correlation coefficient between the spectrum of the first IMF of vibration signals and that of normal state signals will be different as the fault begins to occur. Based on this consideration, the normal state signal and the first IMF of vibration signal are used in order to detect a change of behavior due to the presence of a fault, and the correlation coefficient can demonstrate the fault evolution process and detect an early fault. Finally, using the envelope analysis technique, the proposed method is able to discover the source of the fault and complete a diagnosis.

The fault diagnosis method is given as following:

(1) The raw vibration signal is collected when the roller bearing is normal, and the signal is designated as $x\left(t\right)$. Perform FFT to $x\left(t\right)$, then the signal in the frequency domain, viz. the spectrum $F_{norm}\left(f\right)$ is obtained, where $f$ stands for frequency.

(2) Treat the subsequently collected vibration signals as the ones to be detected. According to the above analysis, these signals are decomposed into a number of IMFs and the first IMF is selected. Perform FFT to these first IMFs, and the corresponding signals in the frequency domain $F\left(f\right)$ are obtained in the same way.

(3) Calculate the correlation coefficient $\rho$ between $F_{norm}\left(f\right)$ and $F\left(f\right)$.

(4) Observe the change of the correlation coefficient and complete the fault detection. Before the fault occurs in the roller bearings, the correlation coefficient maintains at a stable level. If there appears a fault in the roller bearings, the correlation coefficient will begin to become smaller and smaller. That is because the difference between the spectral contents of $F_{norm}\left(f\right)$ and $F\left(f\right)$ will become bigger and bigger as the defect forms in the roller bearings.

(5) Analyze the vibration signals with incipient fault using envelope analysis technique. Considering there may exist several resonant frequency bands, in order to not omit the weak faulty information, the first 4 IMFs are chosen to do the envelope analysis. First, performing the Hilbert transform to the first 4 IMFs components, we could have:

And then the envelope signals could be obtained:

Finally we can get envelope spectrum of the envelope signals by performing envelope analysis to them.

(6) According to the envelope spectrum, the bearing characteristic defect frequencies and harmonics of these frequencies can be recognized in early stages of the faults.

5. Application

In order to check the performance of the proposed method, an example on fault detection and identification of roller bearings is conducted in this study. Most bearing diagnostics research involves studying bearings with simulated or “seeded” damage, which can not reflect the natural defect propagation in the early stages. Therefore, in order to show that the proposed method is capable of detecting and identifying a bearing fault at an incipient stage of the failure, the data obtained from a laboratory test-to-failure experiment is used.

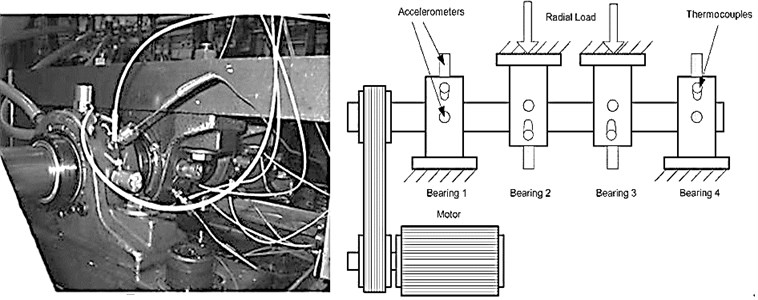
The bearing vibration data comes from the Center on Intelligent Maintenance Systems (IMS), University of Cincinnati [20]. The bearing test rig is shown in Fig. 1, which consists of one shaft, four test bearings, an AC motor and rub belts. The four bearings were installed on one shaft. The shaft was driven by the AC motor and coupled by rub belts. The rotational speed was kept constant at 2000 rpm and a radial load of 6000 lbs was added to the shaft and bearing by a spring mechanism. The vibration data was collected every 10 minutes for 164 hours at a sampling frequency of 20 kHz. At the end of the test-to-failure experiment, an outer race fault occurred in bearing 1. PCB 352B33 High Sensitivity Quarts ICP accelerometers were installed on each bearing housing in order to register the vibration signals, and the data obtained from the horizontal accelerometer of bearing 1 have been used in the experiments.

Fig. 1The bearing test rig

The characteristic defect frequency of the roller bearing with outer race fault can be estimated by the following equation [21]:

where $f$ is the shaft rotational frequency, $n$ is the number of rollers, $\beta$ is the contact angle between the race and the roller, $d$ is the roller diameter and $D$ is the bearing pitch diameter. In this experiment, the Rexnord ZA-2115 double row bearings have 16 rollers in each row, a pitch diameter of 2.815 in., a roller diameter of 0.331 in., and a tapered contact angle of 15.17° [22]. With this data and equation (7), we can get the calculating result of the characteristic defect frequency of the roller bearing with outer race fault, i.e. 236.4 Hz.

The first 24 hours of captures were used as the signals of normal state and one of them was chosen as $x\left(t\right)$, and then the corresponding signal in the frequency domain $F_{norm}\left(f\right)$ could be obtained. Hereafter, we selected one capture every two hours from the 24th hour to the 164th hour and performed EMD to it for acquiring the spectrum $F\left(f\right)$ of its first IMF. Subsequently, the correlation coefficient between $F_{norm}\left(f\right)$ and $F\left(f\right)$ was calculated in order to detect possible changes of bearing conditions.

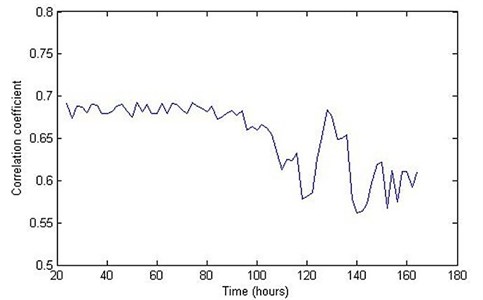
Fig. 2 shows the process of change of the correlation coefficient during the following more than 100 hours. From Fig. 2 we can see that the correlation coefficient begins to drop continuously from about 90 hours and has an obviously overall downward trend during the period between the 90th hour and the 120th hour, which means the defect begins to form gradually in the bearing. 120 hours later the trend of the correlation coefficient rises sharply and then decreases again. This trend may be the result of the “healing” phenomenon which can be explained by the nature of the propagation process of the damage. When the surface defect just initiates, small spalling or cracks are formed and are later smoothed by the continuous rolling contact [22]. As the area of defect grows bigger, the vibration level will rise again, which means that the correlation coefficient will drop and start to achieve another new relatively stable level.

Fig. 2The process of change of correlation coefficient

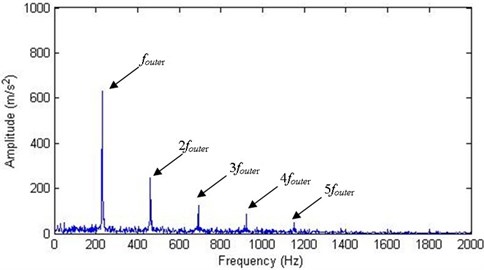
After the fault detection, according to the above analysis, the envelope spectrums of the first 4 IMFs of an incipient faulty signal (90 hours after the beginning of the experiment) were analyzed. By analyzing the envelope signals, it is found that the envelope spectral contents of the later 3 IMFs do not contain any useful faulty information, so only the envelope spectrum of the first IMF is shown in Fig. 3. For comparison Fig. 4 shows the envelope spectrum of the first IMF of an advanced faulty signal (140 hours). In both figures the characteristic defect frequency of outer race fault $f_{outer}=$ 230 Hz, which is very close to the theoretical value, is clearly characterized. As the incipient fault evolves into advanced stage, the amplitudes of the peaks increase, thus making the fault identification more accurate.

By contrast, we can see that the correlation coefficient is extremely sensitive to the occurrence of an early fault. In the practical applications for a specific vibration data, statistics such as standard deviation and mean of the correlation coefficient can be calculated to serve as an indicator of occurrence of an incipient fault. Some safety levels can be acquired by means of the statistics according to the recorded data from the normal bearing condition, and then a warning could be automatically issued when the pre-set levels are exceeded.

Fig. 3Envelope spectrum of the first IMF of an incipient faulty signal

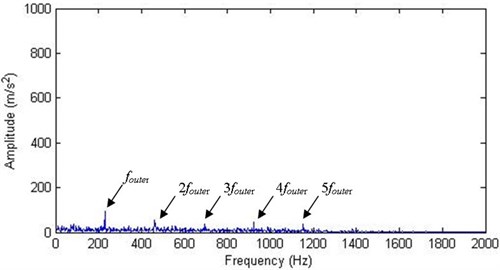
Fig. 4Envelope spectrum of the first IMF of an advanced faulty signal

6. Conclusion

In this paper, we have presented a new method of incipient fault diagnosis of roller bearings based on EMD and correlation coefficient. In the presented approach the EMD method is first performed to the bearing vibration signals to be detected and a number of IMFs are obtained. Allowing for the fact that the spectral content of the first IMF is sensitive to the occurrence of the failure, the correlation coefficient between the spectrum of the signal of normal state and that of the first IMF of the signal being detected is then calculated in order to detect a change of behavior. After the fault detection, envelope analysis is applied to the first 4 IMFs of the incipient faulty signals by means of the self-adaptive nature of EMD, and then the fault type can be identified. In addition this methodology has the potential capability of automatic fault detection. The experimental results demonstrate that the proposed method is effective for the fault detection and identification at early stages.