Spatial performance of skewed continuous rigid-frame bridges based on finite element analysis

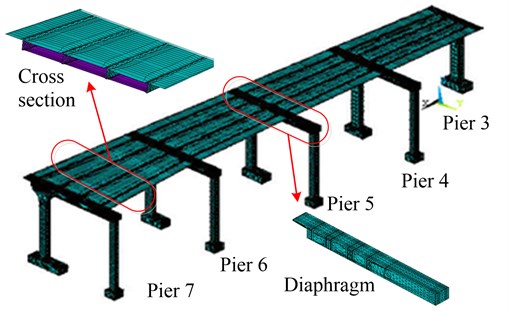
2.1. Boundary conditions

At the bottom of each pier, fixed boundary conditions are applied as restraints of the vertical, longitudinal and lateral displacements. From pier 4 to 7, the main girder is rigid connected to the main pier, and the cantilever end of diaphragms are rigid connected to auxiliary pier at each support. At pier 3, the main girder is simply supported on the pier, which means only vertical restrains exist between the main girder and the pier.

2.2. Loading conditions

According to General Code for Design of Highway Bridges and Culverts (JTC D60–2004), the dead loads include the self-weight of all structural components of the bridge, the wearing surface of the bridge deck, and the attached appurtenances. According to General Code for Design of Highway Bridges and Culverts (JTC D60–2004), the live load includes the design truck load and design lane load. The arrangement of live loads on the bridge is selected to produce the maximum load effect on the critical sections. The temperature change of global system is considered with a magnitude of 20 Celsius degree, and the temperature gradient along vertical concrete deck direction is considered as 5 Celsius degree [14-16].

The brake force is applied according to Section 2.3.3 of JTG D60-2004. Four sets of settlements are considered as below:

• Set 1: 0.5 cm settlement at pier 3, 5 and 7;

• Set 2: 0.5 cm settlement at pier 4 and 6;

• Set 3: 1.0 cm settlement at pier 3, 5 and 7;

• Set 4: 1.0 cm settlement at pier 4 and pier 6.

In the models, different combinations of loads mentioned above were considered to find the unfavorable stress and deflection during service time [17-19].

2.3. Material and properties

A nonlinear elastic isotropic material model is used for concrete in the elastic range, with an elastic modulus of 35 GPa and Poisson’s ratio of 0.1667. The density of concrete is 26000 N/m³ with expansion coefficient 1.2E-5. For pre-stressed tendon, a linear elastic isotropic material model is used with an elastic modulus of 200 GPa and Poisson’s ratio of 0.3. The density of steel is 78500 N/m³ and the expansion coefficient is considered as 1.2E-5. The nonlinear elastic analysis was developed thereafter.

3.1. Normal stress

Normal stress is obtained to find the locations of stress concentration. Since the effects due to temperature changing are very complicated, individual analysis about the temperature was developed first. It is found that the global temperature changing has a little effect to the main girder and diaphragms, but has significant effect to the piers; the temperature of concrete deck has some effects to the main girder and diaphragms in longitudinal direction, but negative effect to the diaphragms transversely, and a little effect to the piers.

Under the unfavorable combination of the dead load, live load, pre-stress tendon, settlements and temperature, for the main girder, the normal stresses of top plate, bottom plate and web distributed uniformly, and the stresses meet the design criteria. For each diaphragm, at the cantilever part, the tensile stress is big, which needs more pre-stressed tendon and reinforcements. The numbering of diaphragms is corresponding to that of piers. As shown in Fig. 2, diaphragm 4 and diaphragm 6 have larger tensile stress on the top. The maximum tension stress is around 2.3 MPa, and for tension field, more reinforcements are needed to reduce cracks. The reason is that more pre-stressed tendons were arrenged and induced the girder hogging and the first span rotated. The pre-stressed tensons were designed based on 2D analysis, which is not a proper way for the actual behavior of the structure. Diphragm 6 at pier 6 has tension at the cantilever part, where the reinforcements must be enforced. Diaphragms 5 and 7 have less than 1 MPa tension, and most field are in compression.

Fig. 2Normal stress distributions of a) pier 4, b) pier 6

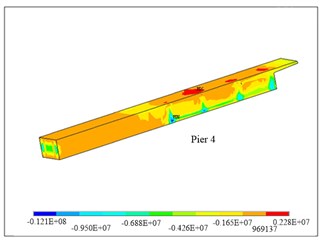
a)

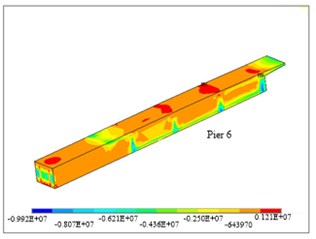
b)

Fig. 3Transverse stress distribution of diaphragm 4: a) diaphragm, b) four layers

a)

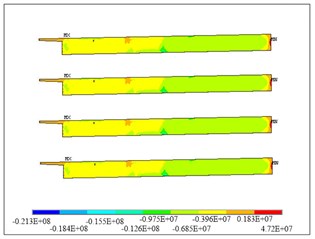
b)

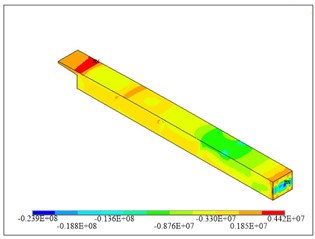
Fig. 4Transverse stress distribution of diaphragm 6: a) diaphragm, b) four layers

a)

b)

3.2. Transverse stress

Under the unfavorable combination of load, the transverse stresses distribute uniformly and not big at top plate, bottom plate and web. The transverse tensile stresses at interior diaphragms, however, are big, which mainly distributes in the junction area of the diaphragm cantilever and the main girder. This is mainly because of the complicated configurations at this area and hence stress concentrations caused by the self-weight of diaphragms cantilever. Therefore, an enhancement or reinforcement at this location is required based on the finite element analysis.

On pier 4, due to over arrangement of transverse pre-stress tendons, the main girder is hogged and the span between pier 3 and pier 4 has large torsion, causing remarkable local tensile stress. During service time the girder between piers 3 and 4 needs to be monitored to avoid large cracks.

For the unsymmetrical structure in transverse direction, except to make the diaphragms meet design, the amount and the shape of pre-stress tendons are designed considering the torsional effect due to un-symmetrical geometry. The unbalanced forces easily induce torsion in girders.

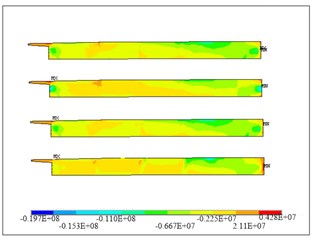
At diaphragm 4, as shown in Fig. 3, the stress at the top of main pier is relatively high due to the pre-stress tendon in the diaphragm, which bends too early on top of the main pier; for this location, there is also relative large bending moment in the transverse direction, which induced more tension at the top of pier; most fields are in compression. At diaphragm 5, the transverse tensile stresses are smaller than that of diaphragm 4. In the similar manner, as shown in Figs. 4 and 5, the transverse tensile stresses at diaphragms 6 and 7 are higher due to the pre-stress tendon design.

Fig. 5Transverse stress distribution of diaphragm 7: a) diaphragm, b) four layers

a)

b)

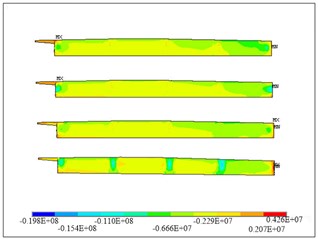
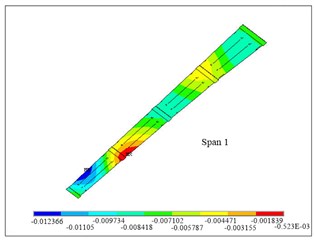
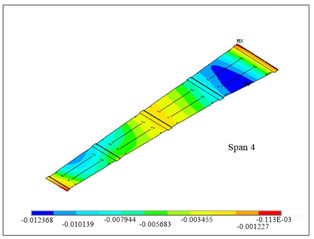
Fig. 6The maximum deflection at bottom plate of a) span 1, b) span 4

a)

b)

3.3. Deflection

For each span under the most unfavorable loading combination, the first and fourth spans have larger deflection than others. The combination of dead load, pre-stressed tendons, and the lane load at first and third spans with truck load at first span cause maximum deflection at first span (between pier 3 and pier 4). The maximum vertical deflection at the top plate is 1.5 cm, and the maximum vertical deflection at the bottom plate is 1.2 cm. The combination of dead load, pre-stressed tendons, and the lane load at second and fourth span with truck load at fourth span causes the maximum deflection at the fourth span. The maximum vertical deflection of top plate is 1.4 cm and 1.2 cm for the bottom plate. Figure 6 shows the deflection at first and fourth span. The maximum deflection at fist span occurs in the right angle line, while the maximum deflection occurs near skewed line.

3.4. Shear lag

According to general beam theory, for wide box section, the normal stress distribution along width is uniform at flanges. Actually when box girders bend, the normal stresses of flanges distribute in a shape of curve due to non-linear distribution of shear deformation, and the normal stress distribution along width is not uniform, which is called shear lag. According to the classical definition, if the normal stress at the flange and web connection is larger than that calculated by the general beam theory, it is called positive shear lag; otherwise, it is called negative shear lag. The coefficient of shear lag $\lambda$ is usually to measure the changing of shear lag, which is defined as follows:

where:

${\sigma }_{max}=$ maximum normal stress considering shear lag;

$\stackrel{-}{\sigma }=$ normal stress calculated based on the general beam theory.

If the stress is larger than the theoretical value that $\lambda >1$, it is called positive shear lag; while $\lambda <1$, it is called negative shear lag.

Tables 1 and 2 show the coefficient of shear lag under dead load and combination of deal load and pre-stressed tendons at the sections of each support and middle sections of each span. From the table, the effect of shear lag is significant at supports. Table 1 shows the coefficient of shear lag under dead load, which varies from 1.06 to 3.06. The effect is barely noticeable at the middle span of span 1 and 4, but significant near pier 4 and 6. Table 2 shows the coefficient of shear lag under dead load and pre-stressed tendons. The coefficient of shear lage is larger pier 4 and 6. The effect of shear lag is more significant than that in the middle span. The girder is in compression at top and bottom plate of both middle span and piers.

3.5. Stress distribution at piers

There are two types of piers including main pier and auxiliary pier for each support. Considering the effect due to dead load, live load, and temperature changing, each pier was analyzed accordingly. The piers are rigid connected to the main girders, which also carry bending moment in longitudinal direction and transverse direction. Based on the FE analysis at pier 4, each pier has larger tensile stress under the unfavorable combination. The reason is addressed as in the fact that more transverse pre-stressed tendons are arranged, but the cantilever part is short which has less selfweight. At pier 7, the top of main pier and auxiliary pier have larger tensile stress. Pier 7 only carries one span, but the main girder and piers are rigid connected, where the negative moment is very large. More reinforcements are needed at pier 7. Figure 7 shows that there are large tensile stresses at pier 4 and pier 7.

Fig. 7First principle stress at a) pier 4, b) pier 7

a)

b)