A hybrid objective function for damage identification via imperialistic competitive algorithm (ICA)

1. Introduction

When a crack occurs in the structure, it affects the dynamical properties of that structure; for example it decreases the bending stiffness and/or increase the damping of structures. The damage detection process using vibration data is usually categorized in four major types: natural frequency based methods, mode shape based methods, curvature/strains based methods and methods based on suing both mode shape and frequency. Doebling et al. [1] presented a review of vibration based damage detection (VBDD) methods. Pandey and Biswis [2], proposed a damage detection technique by using changes in modal flexibility and comparing the flexibility matrices of the intact and damage structures. They evaluated their method with the help of numerical and experimental models and studied the effect of the number of measured modes. Since two last decades, VBDD using optimization algorithms has been an exciting scope for researchers. One of the most practical algorithms is the Genetic Algorithm (GA) which was first introduced by Holland in mid-1960s [3]. Jaishi and Ren [4] used GA to minimize the objective function consisting of the modal flexibility residual, and then identified location and damage size for a simply supported beam. They propose a damage detection technique procedure based on finite element (FE) model updating and modal flexibility residual. Perera et al. [5] used two different objective functions which were the combination of flexibility matrix and modal assurance criterion (MAC). They studied the performance of multi-criteria damage identification GA. Ruotolo and Surace [6] proposed a procedure based on the modal parameters to identify damage and its severity in a multiple cracked beam using genetic algorithm. They evaluated their method by using both numerical simulations and experimental tests for a cantilevered steel beam. Hao et al. [7] used three various parameters, namely, frequency changes, mode shape changes and a combination of the two. They formed an objective function by comparing the changes in the measurements before and after occurring damage and then used GA for minimization process. They evaluated their approach by using both numerical results and laboratory tests, and they showed that their technique is practical even if the analytical model is not accurate. Using the other optimization techniques is also reported including ant colony optimization [8], particle swarm optimization (PSO) [9], hybrid particle swarm optimization [10]. In this work, damage localization problem in beam-type structures is solved with the help of first four natural frequencies and mode shapes. First, an objective function is proposed with the help of hybrid vibration data. Then, an evolutionary algorithm called ICA is utilized in the damage detection procedure. Accuracy of the proposed approach is shown by considering two case studies. In addition, obtained results of ICA-based approach are compared with PSO-based approach.

2. Imperialistic competitive algorithm

This algorithm was first proposed by Atashpaz-Gargari and Lucas [11]. The first step to implement this algorithm is to choose an initial number of populations which are called countries. In this algorithm each country is a $1\times N$ array that is equal to a chromosome in GA. The cost for a country is found by evaluating the $f$ which is a function of $(p_1,p_2,p_3,...,p_{N_{var}})$ variables:

From social-political viewpoint, the unknown variables of cost function are historical and cultural identities of a country. For determining the initial empires, some of the best countries are selected as imperialists and the remaining countries from their colonies. Next step is to adopt the assimilation policy with the aim of evaluating the cultural and social structure of the colonies. In fact, a central government tries to assimilate the colonies. The next step to model the algorithm is to replace the imperialist with a colony, which is approaching the imperialist, when this colony achieves a better situation compared to its imperialist (i.e. this colony finds a point in which it has a lower cost in comparison to the imperialistic approach). In this situation, imperialist and colony will change their positions with each other and new imperialist starts to apply the assimilation policy to the colonies. Then, empires start to compete and each empire which cannot increase its power during the imperialist competitive will be eliminated. In order to increase their power, imperialists have to develop their colonies. Over time, colonies come close to the imperialists in terms of power and a kind of convergence process is observed. The algorithm continues to progress until the convergence condition is satisfied. Having a unique empire in the world along with the colonies which are very close to the empire in terms of position is the ultimate goal of the imperialist competitive algorithm.

3. Method of damage detection

4. Objective function

5. Case studies

5.1. Numerical example

Fig. (1) is shown a clamped-free aluminium beam with Young’s modulus 71 GPa, and density $\text{2210}\text{kg/}{\text{m}}^{\text{3}}$ which is simulated by the finite element model of Euler-Bernoulli beam.

Fig. 1FE models of clamped-free beam

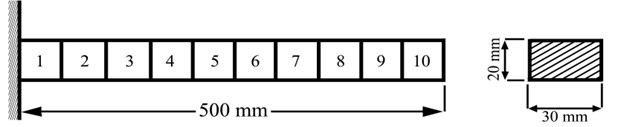
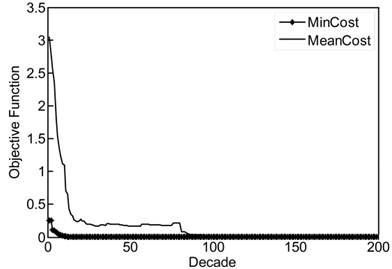
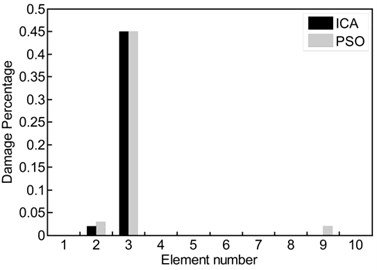
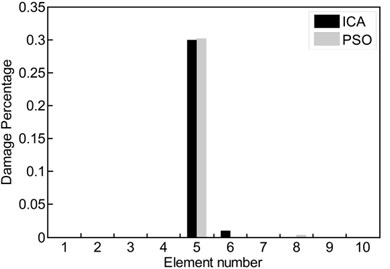
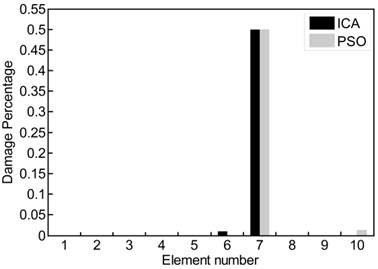
Fig. 2a) ICA feature selection searching for optimal solutions in clamped-free beam example; damage percentage obtained of ICA and PSO for different cases: b) case 1, c) case 2, d) case 3

a)

b)

c)

d)

5.2. Computational experiments with Euler-Bernoulli beam

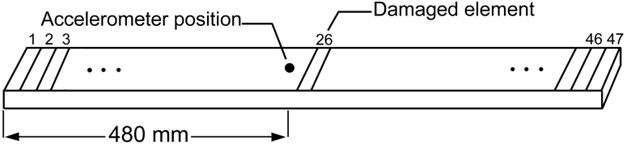
A free-free beam with 47 elements and length $\text{940\hspace{0.17em}mm}$ is simulated by using Euler-Bernoulli beam model. Each node has two DOFs, i.e. translation and rotation. Properties of the beam are as follows: Young’s modulus$E=\text{200\hspace{0.17em}GPa,}$ density $\rho =\text{7860\hspace{0.17em}kg/}{\text{m}}^{\text{3}}\text{,}$ cross-sectional area $A=\text{4.605×}{\text{10}}^{\text{-4}}{\text{m}}^{\text{2}}$ and the moment of inertia $I=\text{3.255×}{\text{10}}^{\text{-9}}{\text{m}}^{\text{4}}$. The beam was excited using a hammer type BK8202 and force signal was amplified by an amplifier type BK-2647A. An accelerometer type DJB-A/120 V was placed at 480 mm from left end. A saw cut damage with 60 % extent was induced in 510 mm from the left end which is located at 26^th element. Responses and force signals were measured and frequency response functions (FRFs) were extracted through PULSE software 8 [14]. The MODENT modulus of ICATS software [15] was used to obtain the first four mode shapes of the beam.

Fig. 3Schematic of free-free beam

6. Results and discussion

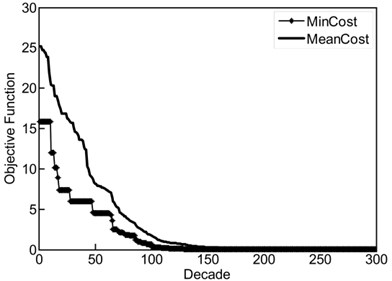
Equation (9) associated with $0\le \beta \le 1$ is the constrained optimization problem which should be solved using ICA. The number of arrays of vector ${\beta }_i$ is equal to the number of elements of the FE model. Based on ICA, the purpose is to find the optimum solution (minimum point) for the objective function. Search for the minimum point is equivalent to search for damaged element. Damage severity of an element is considered as a stiffness reduction factor $\left(\beta \right)$ and running parameters of ICA and PSO are shown in Table 1. The numerical case study is illustrated in Fig. 1. Fig. 2a shows ICA feature selection searching for optimal solutions in clamped-free beam example.

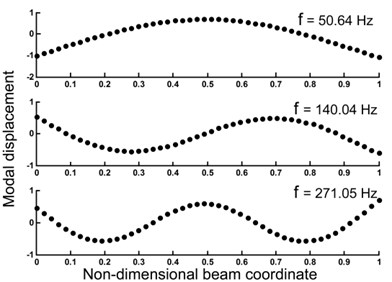
The estimated damage percentage (obtained from ICA) is compared with the outcomes PSO-based procedure in Figs. 2(b)-(d). In these figures, three different damage scenarios (Table 2) are considered over clamped-free beam, and the obtained results show that the hybrid objective function proposed can detect the location and the extent of the damage accurately. In the first case (Fig. 2(b)), when 45 % damage was considered in the third element, both algorithms ICA and PSO (black and gray columns, respectively) predicted the location and the extent of the damage accurately. In cases 2 and 3 (Figs. 2(c)-(d)), 30 % and 50 % damages were considered in fifth and seventh elements, respectively. With the help of proposed method, both algorithms were predicted the location and the extent of the damage with acceptable accuracy. However, there are often differences between obtained results from numerical simulation and what happens in reality. In the model-based methods, the main problem arises from the non-accuracy of FE model of the structure. In this task, we use experimental test data of a free-free beam in conjunction with a FE model to discern damage site. Fig. 3 shows a schematic model of the beam. Fig. 4(a) provides ICA feature selection searching for optimal solutions in the experimental case study. In Fig. 4(b) the first three frequencies and mode shapes of damaged beam are shown. Fig. 5(a) represent the estimated severity and location of damage for the free-free beam. Increasing the number of iterations leads to the reduction of error in predicting the location of damage. In Fig. 5(b), obtained result from ICA is compared with the result of PSO-based procedure where first four vibration data (frequencies and mode shapes) of the structure are used.

Fig. 4a) ICA feature selection searching for optimal solutions, b) the first three frequencies and mode shapes of damaged beams (obtained by test)

a)

b)

Fig. 5a) Effect of number of iterations in damage localization, b) comparison between damage estimated by ICA and PSO

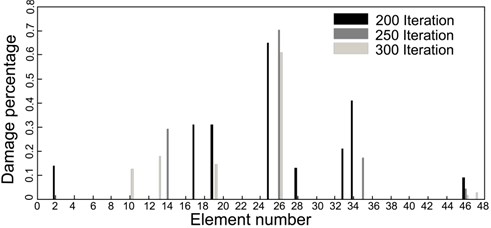
a)

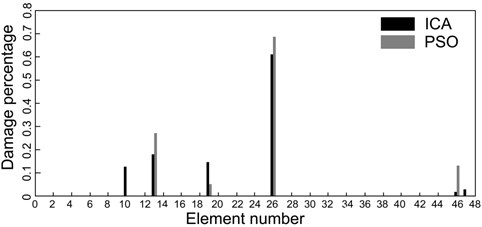
b)

7. Conclusions

In the present study, the aim was solving the inverse problem of damage detection using an evolutionary optimization algorithm called ICA. First, an objective function based on natural frequency and modal strain energy was proposed. Then, two case studies (numerical and experimental) were used to show that this function is able to identify the severity and location of the damage accurately. In this task, damage localization was performed without model updating and it was observed that a non-accurate model of the beam structure can be used in the damage detection process. Due to the difficulties in measuring all of the vibration modes in modal testing, a mode selection strategy was used based on selecting the lowest measured modes. These modes finally formed the modal strain energy. Furthermore, a comparison was drawn between the obtained results from ICA-based approach and result of PSO-based approach whereas the former was able to estimate damage in terms of its extent and site better.