Optimal time delay control for nonlinear vibration of single walled carbon nano-tube on elastic medium

1. Introduction

Carbon nano-tubes (CNTs) hold promise for a number of scientific and technological applications. CNTs are components of nanoscale dimensions that simultaneously present novel physical, mechanical and electrical properties. These properties have made them potentially useful for many applications in nanotechnology, electronics, optics and other fields of materials science [1-2]. In particular, CNTs oscillators have been proposed for use in ultrasensitive mass detection, radio-frequency signal processing, and as a model system for exploring quantum phenomena in macroscopic systems. They are stiffest material known, have low density, ultrasmall cross-sections and can be defect-free. As a result, progressive research activities regarding CNTs have been ongoing in recent years.

Recently, many investigations focused on the modern nanotechnology involving carbon nano-tubes (CNTs) embedded in an elastic matrix [3-5] or resting on an elastomeric substrate [6], in which the CNTs are modeled as a beam pinned at both ends and resting on an elastic foundation. These nanostructured materials can undergo large deformations within the elastic limit and their nonlinear analysis is clearly essential. Fu et al. [5] studied the nonlinear vibrations of embedded nano-tubes by using the incremental harmonic balanced method (IHBM). Postbuckling, nonlinear bending and nonlinear vibration analyses were presented for single-wall carbon nano-tubes (SWCNTs) rested on a two-parameter elastic foundation in thermal environments [7]. Ansari et al. [8] studied the problem of the nonlinear vibrations of multi-walled carbon nano-tubes embedded in an elastic medium using a variational approach. The axial vibration of single walled carbon nano-tube embedded in an elastic medium is studied using nonlocal elasticity theory [9]. Mahdavi et al. [10] studied the nonlinear vibration of a double-walled carbon nano-tube embedded in a polymer matrix. Cigeroglu and Samandari [11] studied the nonlinear free vibration of double walled carbon nano-tubes by using describing function method with multiple trial functions. The nonlinear free and forced frequency analysis of SWCNTs considering intertube radial displacement and the related internal degrees of freedom rested on elastic foundation were investigated based on the continuum mechanics and an elastic beam model [12]. As the excitation magnitude is increased, nano-tube resonators display distinct nonlinear charateristics due to the relatively small dimensions of nano-tubes. The effective resonance bandwidth of such devices can be altered as a result of the presence of nonlinearities [13]. Some NMES devices, such as the carbon nano-tube and nanowire resonances, can transit from a planar motion to a whirling [14]. Therefore, it is important to investigate the suppression control of the nonlinear vibration of the CNT beams.

Studies on the influence of external longitudinal magnetic fields on carbon nano-tubes have also been reported. Wang et al. [15] investigated the effects of a longitudinal magnetic field on wave propagation in carbon nano-tubes (CNTs) embedded in an elastic matrix. Dynamic equations were derived by considering the Lorentz magnetic forces. Narendar et al. [16] developed a nonlocal beam model to study wave propagation in single-walled CNT subjected to a longitudinal magnetic field. Recently Murmu et al. [17] presented an analytical approach to study the effect of a longitudinal magnetic field on the transverse vibration of a magnetically sensitive double-walled carbon nano-tube (DWCNT) based on nonlocal elasticity theory.

Recently, stabilization of beam with delayed feedback has raised many researchers’ interests. Mohammed et al. [18] presented a comprehensive investigation of the effect of feedback delays on non-linear vibrations of a piezoelectric actuated cantilever beam. Khaled et al. [19] investigated the effect of time delays on stability, amplitude, and frequency-response behavior of a beam and found even the minute amount of delay can completely alter the behavior and stability of the parametrically excited beam. Mustapha and Mohamed [20] examined the control of self-excited vibration of a simply-supported beam subjected to axially high-frequency excitation. The primary resonance of a cantilever beam under state feedback control with a time delay was investigated [21]. Vibration control and high-amplitude response suppression could be performed with appropriate time-delays and feedback gains. Qian and Tang [22] discussed the primary resonance and the subharmonic resonances of a non-linear beam under moving load by using time-delay feedback controller. Gohary et al. [23] studied the vibration suppression of a dynamical system to multi-parametric excitations via time delay absorber. The primary, subharmonic, and superharmonic resonances of an Euler-Bernoulli beam subjected to harmonic excitations are studied with damping and spring delayed-feedback controllers [24].

The main purpose of the present study is to suppress the primary resonance vibrations of a CNT nonlinear oscillator rested on the elastic medium with periodic excitation using linear time delay controllers. The Lorentz force of a longitude magnetic field is utilized to control the nonlinear vibration of the SWCNT. A method of determining the regions of the time delays and feedback gains of the stable vibration will be given based on the analysis of the stability conditions of eigenvalue equation. The control parameters will be calculated by the method of minimum optimal method, which takes the attenuation ratio as the objective functions. The optimal controller is designed to control the dynamic behaviors of the nonlinear dynamic system.

2. Program formulation

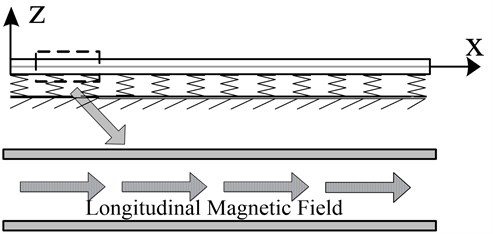
The nonlinear vibration system under consideration is a simply supported CNT of length $L$, mass of per unit length $\rho A$, cross-sectional area $A$ and cross-sectional moment $I$, embedded in an elastic medium (see Fig. 1). Assume that $w\left(x,t^{*}\right)$ is displacement corresponding to the vertical direction, in terms of the spacial coordinate $x$ and the time variable $t^{*}$. The nonlinear equation of motion of CNTs subjected to an external excitation and a magnetomotive control force is given as [12]:

where $f\left(x,t^{*}\right)$ is the excitation per unit axial length. $k$ is a constant determined by the material constants of the surrounding elastic medium. $kw$ is the interaction pressure between the outer-most tube and the surrounding medium. $g_f=\chi A{H}_x^2$, $H_x$ is a longitudinal magnetic field applied to the carbon nano-tube along $x$ direction, $\chi$ is the magnetic permeability [15-17, 25]. As the nano-tube is simply supported at the two ends, the unknown function $w\left(x,t^{*}\right)$ may be given as [12, 26]:

Fig. 1Schematic of single-walled carbon nanotube under the longitudinal magnetic field

One may obtain the following nondimensional nonlinear differential equation of the system:

where $r=\sqrt{I/A}$,$q=\frac{\zeta }{r},\mu =\frac{\eta }{2\rho A\epsilon },\alpha =\frac{{\omega }_L^2}{4\epsilon ({\omega }_L^2+{\omega }_k^2)},F=\frac{1}{\rho ArL\epsilon ({\omega }_L^2+{\omega }_k^2)}{\int }_0^{L}f\left(x\right)\mathrm{s}\mathrm{i}\mathrm{n}\frac{\pi x}{L}dx,$

$g=\frac{{\pi }^2{g}_f}{2\rho A{L}^2\epsilon ({\omega }_L^2+{\omega }_k^2)},t=t^{*}\sqrt{{\omega }_L^2+{\omega }_k^2},{\omega }_k=\sqrt{\frac{K}{\rho A}},{\omega }_L=\frac{{\pi }^2}{L^2}\sqrt{\frac{EI}{\rho A}}$.

Introducing the time delay in a closed circuit, the oscillating current that can cause the Lorentz magnetic forces in the carbon nano-tube will be delayed with a fixed time. The dynamic equation (3) of the nano-tube with time delay is rewritten as:

For the case of primary resonance, the amplitude of excitation and frequency are such that:

Using the method of multiple scales [27], an approximate solution of equation (1) can be assumed as:

Substituting equation (6) into equation (4) and equating the coefficients of like powers of $\epsilon$, we have:

where $D_n=\frac{\partial }{\partial T_n},n=0,\mathrm{}1,\mathrm{}2,\dots .$ A first order approximate solution of equation (7) is:

The amplitude $a$ and phase $\gamma$ of the response are governed by the following polar form of modulation equations:

where ${\mu }_e=\mu +g\mathrm{s}\mathrm{i}\mathrm{n}\tau ,{\sigma }_e=\sigma +g\mathrm{c}\mathrm{o}\mathrm{s}\tau ,\mathrm{}\mathrm{}{v}_e=\frac{3\alpha }{8}$. Setting $D_{1}a=D_1\gamma =0$, we have:

From equations (12) and (13), the frequency-response equation is expressed as:

The amplitude of the response is a function of the external detuning, time-delays, feedback gains and the amplitude of the excitation.

The peak amplitude of the primary resonance response obtained from equation (14) can be written as:

The attenuation ratio can be written as [28]:

As defined by equation (16), for a fixed value of the amplitude of excitation, a small value of the attenuation ratio $R$ indicates a large reduction in the nonlinear vibrations of the primary system. The smaller attenuation rate can be obtained by selecting the proper parameters of feedback gain and time delay.

3. Design of the primary resonance vibration controllers

The stability of the solutions is determined by the eigenvalues of the corresponding Jacobian matrix of equations (12) and (13). The corresponding eigenvalues are the roots of:

The sum of the two eigenvalues is $–{\mu }_e$. If ${\mu }_e>0$, the sum of two eigenvalues is always negative, and accordingly, at least one of the two eigenvalues will always have a negative real part. Based on the analysis mentioned before, the sufficient conditions of guaranteeing the system stability are [30]:

The value of $f\left({\sigma }_e\right)$ is positive value when there is no solution of equation $f\left({\sigma }_e\right)=0$. Letting ${\mu }_e^2\ge v_e^2{a}_{\mathrm{m}\mathrm{a}\mathrm{x}}^4\ge v_e^2{a}^4$, there is:

When there are two solutions of equation $f\left({\sigma }_e\right)=0$, the solutions are:

As the image of $f\left({\sigma }_e\right)=0$ is the parabola whose mouth is opened upward, the inequality of $f\left({\sigma }_e\right)>0$ is satisfied when ${\sigma }_e<{\sigma }_e^{-}$ and ${\sigma }_e>{\sigma }_e^{+}$. Reducing or enlarging the roots of the equation of $f\left({\sigma }_e\right)=0$, we have:

Considering the formula of ${\sigma }_k$ and (22), the stable vibration region is obtained:

Taking into account the formula (23), there is:

4. Optimization design of controller parameters analysis

The regions of feedback parameters have been obtained based on the analysis of the stability condition of nonlinear vibration system, but it is difficult to obtain the optimal control parameters of the system. Taking the attenuation ratio as the objective function, the optimal feedback control parameters can be calculated by the optimal method. An optimal analysis is carried out by taking into account the case that there is no solution or two solutions for the characteristics equation.

5. Simulation research

In the numerical computation, the parameters of material and geometry are taken as $\rho =$ 2300 kg/m³, $E=$ 1.1 TPa, $L=$ 60 nm, unless otherwise specified. The fixed parameters are such that the outside diameter is $d=$ 3 nm, the inside diameter is $d_i=$ 2.32 nm. When length to outer diameter ratio $L/d$ of single walled carbon nano-tubes is considered, the value of spring constant is $k=$ 10⁷, unless otherwise specified. The damping coefficient $\eta =$ 0.01 Ns/m.

Fig. 2 shows the variation of peak amplitude $a_{max}$ with time delays for different feedback gains $H_x$. The amplitude of the distributed force $f$ is 0.3e-12 N/m. It is easily noted that $a_{max}$ varies significantly with the increasing of time delay. For a fixed time delay, the increase of the feedback gains leads to the decrease of the peak amplitudes. For a fixed feedback gain, the increase of the damping can lead to the decrease of the peak amplitude. A well selected value of time delays and feedback gains can relatively lead to a smaller peak amplitude $a_{max}$.

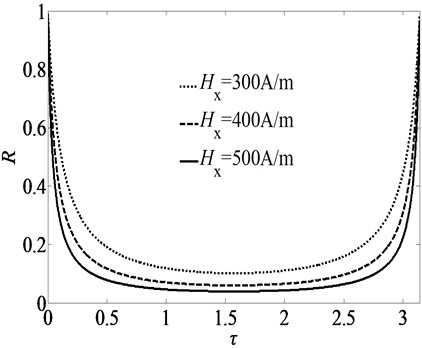
Fig. 3 displays the variation of attenuation ratio $R$ with time-delay and feedback gain. As it is shown in the figure, for a fixed value of the amplitude of excitation, a smaller value of the attenuation ratio $R$ indicates a larger vibrational reduction for the nonlinear vibration system. A properly selected value of time-delay can relatively lead to a larger positive value of ${\mu }_e$ and a smaller attenuation ratio $R$. Therefore, the amplitude of vibration of the nonlinear system can be reduced by properly selecting the feedback gain and the time-delay.

Fig. 2Variation of amax with time delay for different feedback gains Hx

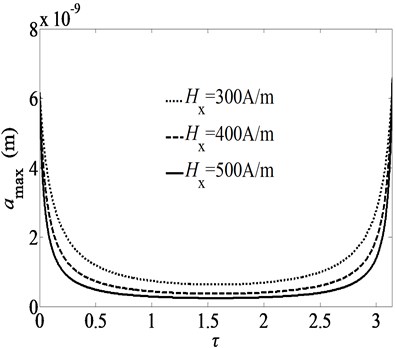
Fig. 3Variation of R with time delay for different feedback gains Hx

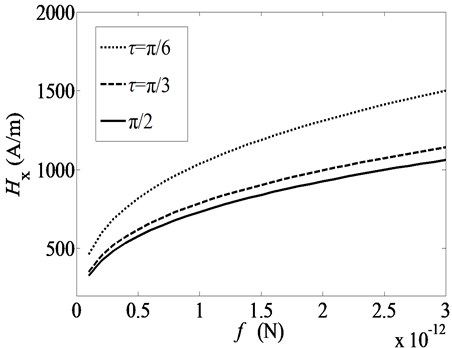
The effect of the excitation amplitude on the stable minimum feedback gains for three sets of time delays is shown in the Fig. 4. The amplitude of excitation $f$ is 1e-12 N/m. The area above the curve means that the feedback gains can lead to a stable vibration and that below unstable. It is also found that $H_x$ is the function of excitation amplitude $f$. When the amplitude of excitation $f$ is a larger value, a larger control parameter is demanded to mitigate the vibration. The optimal time delay can be obtained when $\tau =\pi /2$, in which the smallest feedback gain $H_x$ can be used to reduce the vibration. Therefore, we can take the time delay as a control factor, which can improve the control performance as same as the feedback gain. The optimal control performance can be obtained by selecting an optimal time delay.

Fig. 4Stable minimum control parameters Hx for three sets of time delays

The optimal feedback control parameters can be calculated by using the minimum optimal method. The amplitude of excitation $f$ is 1e-13 N/m. It can be worked out that the value of feedback gain $H_x$ is more than 125.06 A/m when the characteristic equation has no solution. For the case that there are two solutions for the characteristic equation, the optimal feedback gain can be calculated as 397.85 A/m when $\tau =\pi /6$.

Fig. 5 shows the primary resonance curves of vibration system for three different sets of the time delays. The values of the magnetic field vector $H_x$ and amplitude of excitation are 100 A/m and 0.15, respectively. There is no jump and hysteresis phenomenon when $\tau =\pi /6$ and $\tau =\pi /2$.

The saddle node bifurcation and jump phenomenon can be eliminated by choosing certain numerical values of the time delays. Three solutions exist in the case of $\tau =0$ and the jump phenomenon presents. The peak amplitude of the primary resonance response at $\tau =\pi /2$ is the smallest one among the three cases. Properly choosing time delays can effectively suppress the amplitude oscillations of the nonlinear oscillator.

Fig. 6 shows the primary resonance curves of vibration system for three different sets of the values of spring constant. The values of the magnetic field vector $H_x$, time delay, and amplitude of excitation are 100 A/m, $\pi /2$ and 0.15, respectively. The vibration of the system is stable when $k=$ 1e7and $k=$ 1e8 and unstable when $k=$ 1e6. The peak amplitude of the primary resonance response at $k=$ 1e8is the smallest one among the three cases. The spring constant of elastic medium can affect the nonlinear vibration of the SWCNT.

The feedback should be implemented at least in such a way that is ${\mu }_e>0$ guaranteed. Under such feedback gains and time delays, the sum of the two eigenvalues is always negative and accordingly at least one of the two eigenvalues will always have a negative real part. When $f\left({\sigma }_e\right)=0$, the other eigenvalue is zero where a saddle-node bifurcation occurs. We utilize Eqs. (14) and (17) to study variation of the response amplitude with the longitudinal magnetic and the excitation amplitude when $k=$ 10e7 and $\tau =$ 0, as illustrated in the feedback gain-response curve shown in Fig. 7.

The variation of the response amplitude with the frequency detuning parameter $\sigma$ and the excitation amplitude is studied by utilizing Eq. (30) when $k=$ 10e7 and $\tau =$ 0. Fig. 8 illustrates the frequency-response curve when ${\sigma }_A<{\sigma }_B$, in which only a stable trivial solution exists. As $\sigma$ is increased, the trivial solution loses stability at point $C$ and gives way to a branch of stable periodic solutions. The amplitude of these stable solutions increases as $\sigma$ is increased further towards point $C$. At point $C$, the periodic solution loses stability through a saddle-node bifurcation, and the response amplitude jumps down to point $D$ where only trivial solutions exist. Increasing beyond point $D$ leads only to the stable trivial solutions.

Fig. 5Frequency-response curves for primary resonance for three sets of time delays

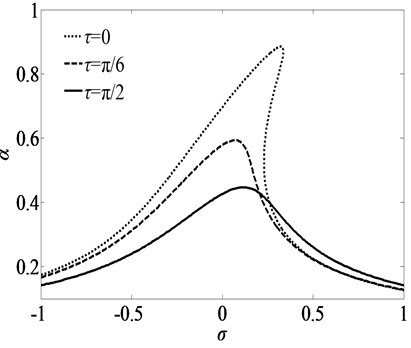
Fig. 6Frequency-response curves for primary resonance for three sets of spring constants

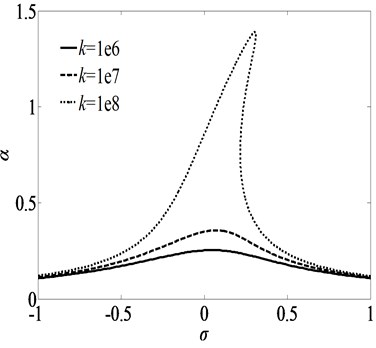
Fig. 7Saddle-node bifurcation of the nonlinear vibration system

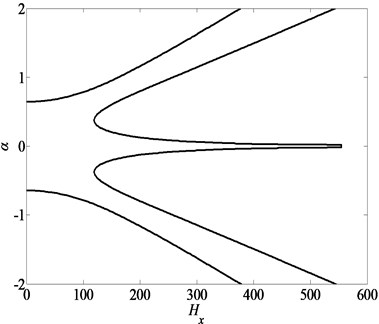
Fig. 8Jump figure of nonlinear vibration system

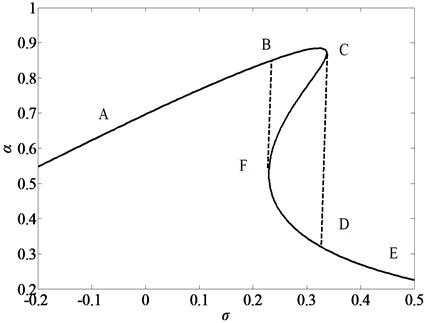
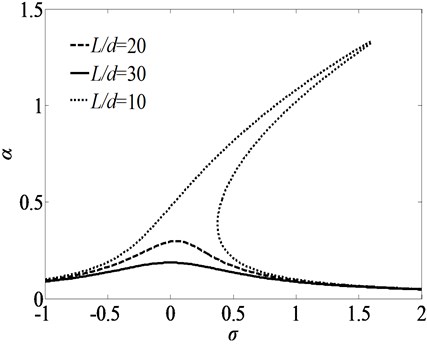
Fig. 9 displays the primary resonance curves of vibration system for three different sets of the diameter-to-length ratios ($L/d$). The parameters are $H_x=$100 A/m, $k=$1e7, time delay $\tau =\pi /2$, and $F=$ 0.1, respectively. There is no jump and hysteresis phenomenon when $L/d=$ 20 and $L/d=$ 30. In contrast, for the case of $L/d=$ 10, three solutions exist and the jump phenomenon presents. The peak amplitude of the primary resonance response at $L/d=$ 30 is the smallest one among the three cases. With the increasing of the ratios of $L/d$, the nonlinearity of the vibration system becomes weaker and the nonlinear phenomenon is easier to be controlled.

Fig. 9Frequency-response curves for primary resonance for three sets of ratios of L/d

6. Conclusions

The Lorentz force of a longitude magnetic field is utilized to control the nonlinear vibration of the SWCNT. The primary resonance of a single-walled carbon nano-tube system rested on the elastic medium is mitigated by using the time delay controllers. The stable regions of feedback parameters are obtained based on the analysis of the stability condition of nonlinear vibration system. The time delays can be used as a control factor, which can improve the control performance as well as the feedback gains. The optimal control parameters are calculated by using minimum optimal method. The optimal controllers are designed to control the dynamic behaviors of the nonlinear dynamical systems. It is found that an appropriate feedback can enhance the control performance of the CNT devices. The optimal feedback time delay can have an optimal control result.