Abstract
The problems of uncertainty modeling and model validation of aeroelastic system are investigated. The parametric uncertainty is considered to denote the uncertainties in structure, and both parametric form and unmodeled dynamics are used to represent the influences and mechanism of uncertainties in unsteady aerodynamic forces. The Linear Fractional Transformation representation of the uncertain aeroelastic system is established to perform model validation and robust flutter analysis. A testing method for the existence of a validating model set in frequency-domain is developed, then the model validating sets are parameterized and the problem of searching the uncertainty magnitudes can be formulated as an optimization process. The influence of exogenous disturbances and noise, which are inevitable in actual testing environment and commonly unknown but energy bounded is considered, and consequently the conservatism of the uncertainty bounds is reduced. At last, for the uncertain aeroelastic system with the obtained uncertainty magnitudes, the robust flutter analysis based on structured singular value theory is performed to predict the robust stability boundary. The comparison of the results associated with two different uncertainty descriptions and the influences of disturbance and noise are discussed. Two numerical examples are presented and the results of the simulation demonstrate the validity of the developed method.
1. Introduction
Flight flutter test is the indispensable test program in airplane development. It is of vital importance not only for the full scale development of an aircraft, but also for the clearance of new configuration (different stores or modification of aircraft) from flutter, which both need these programs to verify the aeroelastic stability and expand the envelope [1-2]. How to predict the flutter boundary accurately and safely in flight flutter test has always been the research objective of aeroelastic community. In recent years, a flight flutter test method based on robust flutter analysis has been developed [3-4]. This method uses structured singular value to evaluate the robust stability of aeroelastic systems and predict the robust flutter margin which could account for the various uncertainties between theoretical model and actual system, such as uncertainties of mass, stiffness and variations of parameters in aerodynamic model and control system. It is not the purely theoretical analysis or testing techniques, but the combination of them.
According to the specific uncertainty description of an aeroelastic system, the worst-case flutter boundary can be calculated [3-4]. The uncertainty description should be capable of representing the errors between the nominal system and actual system reasonably, which means the uncertainty model is neither too conservative nor too optimistic. Whether the predicted robust flutter boundary is of any practical value is almost entirely depends on the description of uncertainty, which includes the sources, structures and magnitudes of the uncertainties [5-7]. The sources and structures of uncertainties can be determined by the properties of the actual system, the related specified problems and even by the engineering experiences. While, the uncertainty magnitudes need to be estimated by suitable model validation process with measured input-output testing data [3]. A reasonable description of uncertainty is the critical premise of robust flutter analysis, and the validity of the uncertainty model is evaluated and verified by model validation [3, 4, 8].
Smith and Doyle [9] first developed a validation method for linear fractional uncertain model in frequency domain. This method used a secondary optimization procedure to solve the validation problem in framework. Chen Jie [10-12] has proved that the method proposed by Smith is difficult for practical application and is only partially solvable. The LFT uncertain model validation method they presented can be applied to both time and frequency-domain measurements and deal with structured and unstructured uncertainty. Moreover, the validation problem could be reduced to a type of Nevanlinna-Pick boundary interpolation problem, which makes it practically solvable. Lim and Balas [13-14] studied the validation problems of uncertainty, of which the structure is characterized by full complex blocks and repeated scalar blocks. The conditions that the uncertain model is not invalid have been proposed and the magnitude of each uncertainty can be obtained by an optimization process. Nevertheless this approach requires transcendental information of the uncertainties, and the diagonal description of uncertainty is tedious and practically difficult to deal with.
Kumar and Balas [15] has developed a model validation method based on inverse LFT theorem. The method uses structured singular value to indicate whether the uncertainty system is invalid or not invalid. This approach makes the validation procedures could be fluently connected with the robust flutter analysis procedures which are both implemented in the framework of theory. According to the theory proposed in [15], Lind and Brenner [3-4] and Borglund [16] employed this method to perform model validation for aeroservoelastic system using flight data or wind tunnel test data. The proportion relationship of the uncertainty magnitudes is designed according to the prior information of the entire system, and the weighting factors are scaled to ensure the uncertain model includes the actual system. However, this method is only suitable for Single Input Single Output (SISO) system and frequency domain data, and the influences of the existing disturbance and noise in real test environment are not considered, which will make the results more conservative.
Lim [17-18] provided easily computable tests for the existence of a model validating uncertainty set. The validation test deal with linear fractional transformation uncertainty structure and allow the unknown but bounded exogenous disturbances to be included. The constraints on the necessity and sufficiency of the test are discussed for both uncertainty structures of full complex blocks and repeated scalar blocks. The essential of the proposed method is parameterization of all model validating sets of plant models, which can be used to perform uncertainty trade-off with model validating uncertainty sets, and the magnitudes of uncertainty with full complex blocks and repeated scalar blocks structures are optimized to reduce the conservatism.
Since the prediction of transonic flutter requires computationally expensive high-fidelity simulation models, traditional uncertainty analysis is not often applied to transonic flutter prediction, and the results have less confidence. Literature [19] investigated various methods to reduce the computational time of traditional uncertainty analysis. Design of experiment and response surface methods and mu analysis are applied to validate an aeroelastic model of AGARD 445.6 wing. Based on reduced-order models, the two methods have shown results that compare very well to the established and widely accepted traditional stochastic Monte Carlo approach. The computational time of the DOE/RSM method is significantly less than Monte Carlo analysis. This advantage will become more obvious as model order and complexity increases. Although the increased run time for -analysis is detrimental, the mathematical guarantee and higher robustness are also extremely valuable.
Chan and Shun [20] used the NASA Dryden Flight Research Center’s multidisciplinary design, analysis, and optimization tool to tune a structural dynamic model of the Aerostructures Test Wing, in order to match the measured data and minimize the model uncertainties. By optimizing the objective function and constraints, the mass properties, natural frequencies, and mode shapes are matched to the target data and the mass matrix orthogonality is retained. After tuning the FE model, the frequency differences between GVT and analytical results are within 3 % and the off-diagonal terms of the orthonormalized mass matrix are within 10 %, satisfying the military standards. Excellent mode shape correlations were also achieved through the high MAC value (greater than 95 %). A 25 % change in flutter speed has been observed after reducing the uncertainties. The author's another work focus on developing an unsteady aerodynamic model tuning methodology for precise flutter prediction during flight test [21]. In this paper, an unsteady aerodynamic model tuning method based on the direct AIC modification is proposed, through which the modeling uncertainties associated with the unsteady aerodynamics can be minimized. The validity of the unsteady aerodynamic model tuning procedure has been demonstrated by the application to the ATW2 flight-test data. The results showed excellent agreement of the flutter speed acquired by computation and flight test respectively, when the tuning procedures of structure dynamic model and unsteady aerodynamic model are all applied.
Researchers from SAAB Aerosystems developed a process for using robust analysis for industrial applications [22]. The process combines robust analysis, flight flutter testing, and model validation in such a way that is suitable for industrial purposes. The robust aeroelastic analysis of a fighter aircraft equipped with a new wingtip missile is performed via - method. The sensitivity analysis is used to choose a suitable uncertainty model to account for the wingtip aerodynamic uncertainties. A coupled procedure combining flight flutter testing, uncertainty model validation and robust analysis is applied to expand the envelope. This investigation showed that the new - method has great potential to be used in the industrial process for aeroelastic airworthiness assessment. The paper also suggests that, before performing robust aeroelastic analysis, it is important to construct a reasonable uncertainty model that is capable to represent the essential dynamical mechanism.
Model-form and predictive uncertainties can become a significant source of uncertainty in engineering systems. Riley [23] introduced a model-form uncertainty quantification method and applied the quantification procedures to an aeroelastic problem. Within this methodology, the Bayesian model averaging approach is implemented to quantify both the predictive and model-form uncertainties. To reduce the modeling uncertainty through experimental data, they use the uncertainty itself to determine necessity and location of additional experimental data points. The modified adjustment factors approach has been developed to calculate the sensitivity of the adjusted models to the model probability assumptions, which could indicate whether the further information of the models could reduce the uncertainty.
In the study presented herein, a model validation method based on Nevanlinna-Pick matrix interpolation theory, which is just mentioned before and provided by [17-18], is successfully applied to validate an uncertain aeroelastic system for two different types of aerodynamic uncertainties. According to the dynamic characteristics of the aeroelastic system, the structure and aerodynamic uncertainties are represented by diagonal blocks structure, which are more concise and have specific physical implications. Compared to the method used in [3-4], the method developed in this paper could consider the structure information of uncertainty and validate each uncertainty individually and more accurately. Furthermore, the influences of exogenous disturbance and noise are also taken into consideration in order to share the errors between nominal model and actual system with uncertainty, which would result in effective reduction of conservatism. In addition, the presented method can be applied to MIMO systems which allow the model to be validated and verified by flight data from multiple channels. An illustrative example is given that include comparisons of candidate model validating sets for different settings, uncertainty structures and trade-off. Another example considers the store aerodynamics as the uncertainties and the numerical results demonstrate the validity of the presented method. The method and results of this paper could provide tools and references for robust flutter analysis and flight testing.
2. Model validation
2.1. Framework of model validation
The generic problem of model validation can be described as follows: If the given uncertain model or the model set can reproduce the measured testing input and output data under the influence of unknown but norm bounded exogenous disturbance and noise, the uncertain model is considered to be a model validating uncertainty set, i. e. the model is unfalsified. Model validation, which is based on certain identification mechanism and optimization algorithm, is a process to determine the magnitudes of uncertainties through measured input and output testing data. In fact, there is no model that can be completely validated by finite testing data, because new measurement may violate the current model. Thus, we can only prove that the model is not invalid, i.e. unfalsified [24].
Fig. 1Model validation framework (a) and canonical form (b)
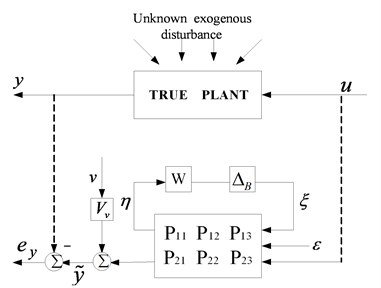
(a)
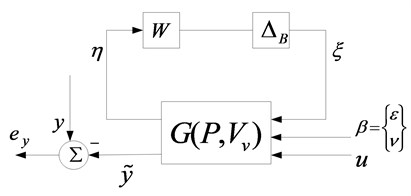
(b)
The LFT framework of model validation and its canonical form is shown as Fig. 1. The inputs and the outputs are the actual signal of the true plant which can be measured in testing, while the simulated output signal of the plant model is a sum of responses exited by noise, disturbances, and known input signal . is the error between measured and simulated output and is the structured uncertainty model defined by Equation (1). Diagonal matrix denotes the weightings of uncertainties and each diagonal element represents the bound of the corresponding uncertainty. and are the internal fictitious signals that relate the uncertainties and the nominal plant. In order to simulate the actual testing environment, measurement noise of the output and exogenous disturbances , which affects the system through the controlled input channel or a separate path, are introduced. Signals and are norm bounded, so the independent bounds on the two signals and are assumed. , ; are the transfer function matrices and consist of an augment nominal model . A noise transfer function matrix and a disturbance transfer function matrix are designed to imbed into the partitioned blocks and of the augmented nominal plant . Both transfer functions are assumed driven by unknown but bounded independent random signals. For convenience, both exogenous disturbances and are combined into a single disturbance vector , which is approximately norm bounded by for mathematical simplicity. For each discrete frequency point, the actual disturbance signal can be considered as , where . Then after the combined disturbance signal is applied, the framework diagram of Fig. 1(a) can be simplified to a more concise form shown as Fig. 1(b), where the transfer function matrices are determined by and . Note also that it is typical in many applications that is assumed known, so if the output error is satisfied, the input error is also equal to zero. Therefore, only considering output error constraint is sufficient for the presented application.
Define the structured uncertainty:
where is the number of uncertainty block and denotes the real number filed or the complex numbers field . A corresponding set of bounded structured uncertainty is defined by:
where the elements of the diagonal matrix:
are the scaling radii applied to the blocks of the structured uncertainty of which the unit ball is defined by .
The transfer relationships obtained from Fig. 1 is shown as follows:
where is the output error of the nominal plant. It is seen from Eq. (7) that the structured uncertainty term and exogenous disturbances term could share the output error jointly. If the output data of the actual system is distorted by the disturbance and the influences are not considered in the model validation framework, the identified uncertainty magnitudes would be overly large which will result in a conservative robust flutter prediction.
Before performing model validation, the transfer function matrix needs to be determined. Assume that, the mean square value and variance of the true measurement noise have been obtained as the prior informations. Then white gauss noise with the same mean square value and variance is simulated to generate signal , which can be used to determine transfer function matrix [18]:
where denotes an point DFT sample used in model validation with sampling interval . is the number of noise channels and is the power spectra of the simulated signal .
2.2. Parameterization of model validating sets
Only if , the norm bounded combined disturbance () and uncertainty output signal can reproduce the given input and output measurements, which means the given model set is not invalidated. Define , then the following equations can be obtained:
In the above equations, is a matrix of which the columns consist of a basis for and the symbol denotes the sub-matrix which is associated with , i.e. the corresponding row vectors extracted from matrices and according to the dimension of in Eq. (10). Parameter is an arbitrary vector with appropriate dimension.
The condition for the existence of a model validating set can be stated as follows: there exists such that Eq. (9) and the inequality are satisfied. In order to find the parameter that satisfies , is decomposed through singular value decomposition (SVD). Then can be parameterized by the new introduced parameter vectors and and is shown as:
In this decomposition, , , , are unitary, is diagonal and nonsingular, and the block matrix partitioning are conformal. Symbol denotes conjugate transpose. and are arbitrary and satisfy and , where and are dimensions of the vectors. Correlate Eq. (13), (10) with (5), the pair of signals are given by the parameterization:
where and are constant vectors and is an identity matrix with a dimension equals to that of . is defined as , where is an identity matrix, of which the dimension is determined by .
According to Eq. (4), the signals and have to be consistent with their transfer relationship through the uncertainty structure . Colum vectors and are the partitioning of vectors and that conforms to the block diagonal partition of in Eq. (1) and their norm ratios determine the uncertainty magnitudes . For repeated and/or real scalar blocks, the collinearity condition is:
and for full complex blocks, another condition Eq. (17) has to be satisfied:
The parameterization of the pair of signals is not unique which means that the validating model with the capability to reproduce the available data is not unique. In order to reduce the conservatism of the results, it is necessary to reasonably design the proportion distribution of the uncertainty weightings/radii and to find the model validating set with the smallest uncertainty magnitudes. A positive factor is introduced in order to simultaneously scale the uncertainty magnitudes according to the designed proportion. Thus, becomes the real uncertainty magnitude. Specifically, a constrained nonlinear optimization process with and as the design variables is used to find a minimal positive such that is a model validating set. So Eq. (17) can be written as:
Thus, the problems can be formulated as a constrained nonlinear optimization problem which is described as follow: the the design variables are , , and ; the constraint conditions are Eq. (16), Eq. (18), and ; the objective is to find the smallest . First, determine the proportion distribution of uncertainty weightings which is obtained by analyzing the priori knowledge and should reflects the true uncertainty mechanism. Second, select initial values of the design variables according to the constraints. Then the problem can be solved with a sequential quadratic programming which is provided by the Optimization Toolbox of MATLAB [25]. After finding the smallest , will characterize the uncertainty magnitude and will be the desired model validation result.
3. Modeling of uncertain aeroelastic system
3.1. Equation of motion
The governing equation of a generic aeroelastic system is:
where , and are the modal mass, structural modal damping and modal stiffness matrices, respectively; is the vector of generalized coordinates, is the dynamic pressure and is the generalized aerodynamic influence coefficient (AIC) matrix, which depends on Mach number and reduced frequency .
The AIC can be obtained by several aerodynamic theories, such as doublet lattice method, ZONA 51 and piston theory et al. In this paper, the doublet lattice method (DLM) was adopted for subsonic unsteady aerodynamic force computation. In aeroelastic community, DLM is a universally acknowledged method for subsonic unsteady aerodynamic force calculation. It was first proposed in 1969 [26], and developed as a classical aerodynamic model for flutter analysis. Several aeroelastic analysis softwares, such as MSC. Flight loads and Dynamics [27], ZONA ZAERO [28], employ DLM or the improved version as one of the core aerodynamic modules.
Based on small disturbance hypothesis, DLM solves the linearized potential flow equation and obtains the aerodynamic forces under the condition that the aerodynamic panel oscillates harmonically. The aerodynamic panel is divided into small trapezoidal lifting elements, where the horse-shoe vortex are assigned to each grid to represent steady flow, and acceleration potential doublets are placed in the 1/4 chord length to simulate additional terms of unsteady aerodynamics. To satisfy the Kutta condition at trailing edge, the middle point at 3/4 chord length of each grid is chosen as the control point, for which the boundary conditions must be satisfied.
The AIC is a set of matrices which are computed for distinct values of reduced frequency. Thus, in order to compute AIC for any desired frequency point conveniently and rapidly and perform time domain analysis, the aerodynamic forces obtained in frequency-domain have to be transformed into time-domain representations. Several methods often referred to as rational function approximations, have been developed to describe the unsteady aerodynamic forces analytically. This paper uses Roger’s formulation [29] to represent the aerodynamic forces which is shown in Equation (20):
In Eq. (20), , , and are coefficient matrices which are solved by approximation algorithm; is defined as , where is the frequency of vibration, is the reference semichord and is airspeed; are the poles used to describe the effects of aerodynamic lags. The formulation used in this paper considers four lag terms to represent the unsteady aerodynamic effects.
3.2. Uncertainty modeling
For complex systems such as a real aircraft, the sources and structures of uncertainty are highly diversified and difficult to be described. The uncertainties of mass (fuel consumption), damping and unsteady aerodynamic force are the significant sources for aircraft systems and the influences of nonlinearities and unmodeled dynamics are also non-negligible. The additive and multiplicative uncertainties also have distinct characteristics. In this paper, the complex influences of uncertainties being derived from numerous sources and being of several structures are not discussed, because the mechanism of uncertainty commonly depends on the specific problems, of which the identification involves profound understanding of aeroservoelasticity and abundant engineering experiences which are not the main purpose of this paper. The source and structure of the uncertainties are only assumed to demonstrate the validity of the model validation method and evaluate the robust flutter predictions. In the presented study, the parametric uncertainties of damping and stiffness are modeled for structure, and both parametric uncertainty and the unmodeled dynamics of unsteady aerodynamic forces are considered and discussed respectively. The uncertainties are formulated as follows:
where and are the nominal matrices, and are used to choose the type of uncertainty [30]. For example, means the multiplying uncertainty and indicates the additive uncertainty. Since , are modal damping and modal stiffness, they are all diagonal matrices. Consequently, and are repeated scalar blocks or real scalar blocks.
Unsteady aerodynamic uncertainties might be the most significant source and have a strong influence on the dynamic behavior of the aeroelastic system [16]. can be obtained by appropriate aerodynamic theory such as Doublet-Lattice Method (DLM). But various simplifications and assumptions are used in the theoretical models which lead to difficulties in accurately modeling of wing tip and control surface aerodynamics. An elaborative modeling of aerodynamic uncertainty is developed by Borglund and discussed in detail in [16]. Here, we just use the method and procedures to model aerodynamic uncertainty without detailed presentation. If the aerodynamic uncertainty is considered as unmodeled dynamics, the description can be formulated as:
where is the nominal aerodynamic influence matrix, is the unknown full complex block and . is the weightings used to scale the unity-bound operator and is the order of nominal plant. If the aerodynamic uncertainty is considered to be parametric, a concise form that accounts for the contributions of modal aerodynamic to the entire generalized aerodynamic uncertainty is adopted and represented as repeated scalar blocks. The parametric uncertainty is written as:
where is a matrix of which the elements are zero except ; is number of the mode that is considered to have remarkable influences on aerodynamic uncertainty. and are also defined.
Substituting the uncertainty expression Eq. (21) and Eq. (22) into the equation of motion Eq. (19), the obtained equation can be written as:
Define and , a concise equation can be obtained as:
Perform Laplace Transformation for Eq. (25), and compute the transfer function from to and to , the transfer function between and is obtained. Then the -analysis loop for robust flutter computation with full complex blocks is shown as Fig. 2.
Fig. 2μ-analysis loop with full complex blocks
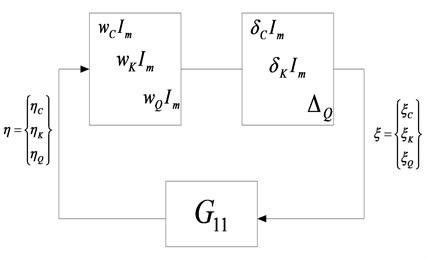
Substituting the uncertainty expression Eq. (21) and Eq. (23) into the equation of motion Eq. (19), the uncertain aeroelastic equation can be written as:
Define and , one can obtain:
The transfer function matrix between and is also obtained and the -analysis loop for robust flutter computation with repeated scalar blocks is shown as Fig. 3.
Fig. 3μ-analysis loop with repeated scalar blocks
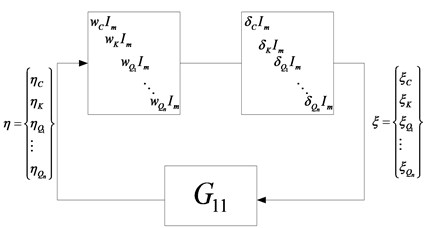
4. Numerical example
The numerical examples presented in this paper use autoregressive method to simulate the actual flight testing. Two aeroelastic models, including a straight wing model and a wing-fuselage-store model are presented. The actual system, nominal system and uncertainty description are all designed and the model validation is performed using simulated input-output data as testing data to estimate the uncertainty magnitudes. After the uncertainty model is obtained, the structured singular value theory is applied to analyze the robust stability of the uncertain aeroelastic system. The values of different flow velocity are used as indicator to determine whether the system is robust stable. Finally, the flutter speed of the worst case is obtained and is defined as robust flutter speed.
4.1. Straight wing model
The finite element model of straight wing with NACA0012 airfoil is modeled using MSC/PATRAN software and is shown in Fig. 4. The unsteady aerodynamic forces are compute for by doublet lattice method and the first ten order of modal mass , modal stiffness , modal damping , generalized AIC and mode shape vectors are exported by DMAP techniques [31]. The generalized AIC matrices of different reduced frequency are approximated by Roger method and then the aeroelastic equation can be transformed to time domain. The modal parameters of actual system are designed as , , and the first 5 orders modal parameters , , and the corresponding generalized AIC matrix are defined as the nominal model. For structure, the parametric uncertainties of stiffness and damping are considered and for aerodynamics, the uncertainty is considered as parametric uncertainty of modal aerodynamics and unmolded dynamics respectively.
Fig. 4The finite element model of straight wing

The excitation signal is applied to the straight wing model and the response is obtained by mode superposition. The simulated input and output signals are all recorded and used as measured data in flight testing. According to the method and procedures described in previous section, the uncertainties of structure and aerodynamics are modeled and the disturbance and noise which is inevitable in real testing environment are introduced to the model validation framework. Finally, the LFT framework of model validation is established. As mentioned before, model validation requires prior information of the system and uncertainty. This information could be helpful for assigning the weightings of each uncertainty and determining the proportion relationship reasonably. For parametric uncertainty of modal aerodynamics, the studied case considers the first two modes are of more importance and provide primary contributions for aerodynamic uncertainties. This is because the generic flutter is caused by two modes unstable couplings and it is easier to determine the weighting proportion for less parameter. However, how to determine the proportion among several uncertainty weightings is a problem involves the study of interaction mechanism of various uncertainties, deriving from different sources and being of different structures. The main purpose of this paper is to present a model validation method and demonstrate its feasibility and validity, so that study is not included.
If the weighting proportion relationship between each uncertainty is determined, the scaling factor is optimized in order to validate the uncertainty model set. In real test, the influence of disturbance and noise is inevitable. If the errors between theoretical model and actual system are entirely ascribed to uncertainties of structure and aerodynamic forces, the magnitudes of uncertainties will be overestimated which would cause a much conservative result of robust flutter prediction. Thus, the influence of disturbance and noise is considered to reduce the conservatism effectively.
The stability of the so-called “actual system” is analyzed by state-space method and flutter speed is obtained as , while the flutter speed of the presupposed nominal model is . For case of parametric aerodynamic uncertainty, the weighting proportion relationship is designed as . The analysis is considered as three different circumstances and discussed respectively, (a) there is no disturbance and noise in real system testing, i. e. , which means it is not necessary to introduce signal to the validation framework and is applied. (b) the influence of disturbance and noise did exist in actual system testing, but the influence is not included for model validation, i. e. . (c) the influence of disturbance and noise did exist in real system testing, and this influence is accounted for by simulated signal in the model validation framework, which would share the modeling errors with the uncertainties together. Table 1 displays the model validation results of the parametric uncertainty for sea level. denotes the robust flutter speed and the unit is m/s.
Table 1The results of robust flutter analysis for different setting conditions
Case | ||||||
a | 0.0404 | 0.0808 | 0.0404 | 0.0404 | 0.0404 | 158.5 |
b | 0.0599 | 0.1199 | 0.0599 | 0.0599 | 0.0599 | 155.0 |
c | 0.0398 | 0.0797 | 0.0398 | 0.0398 | 0.0398 | 158.7 |
According to the model validation results, the robust flutter speed for the three different circumstances can be calculated by toolbox embedded in MATLAB software [32]. The up bounds of values of different speeds are computed and the flight speed corresponding to 1 is defined as the robust flutter speed which is also shown in Table 1.
It can be seen from Table 1 that the robust flutter speeds are lower than the nominal flutter speeds, which demonstrates that the robust flutter boundary takes the uncertainty into consideration and is the flutter speed of the worst-case. The robust flutter speed varies as the uncertainty magnitudes, so different uncertainty magnitudes for the three circumstances, which are obtained by model validation, results in different robust flutter speed.
The weighting proportion of the uncertainties is used for all the three cases, and the results of uncertainty magnitudes and robust flutter speeds are exhibited in Table 1. It is seen that Case (a) is an ideal condition that excludes any disturbance and noise from the actual system and the influence of them is also not considered in model validation. The errors between nominal model and actual system are entirely ascribed to uncertainties and the magnitudes are estimated according to this assumption. But the influence of disturbance and noise is inevitable and even strong in actual system and real test environment. If their influences are not taken into account in model validation, the errors between nominal model and actual system will be entirely undertaken by uncertainty which will result in larger estimation of uncertainty magnitude and conservative robust flutter prediction. Results of Case (b) demonstrate this clearly. The uncertainty magnitudes are much larger than those of Case (a) and the predicted robust flutter speed is also much more conservative. As for Case (c), the terms of disturbance and noise are formulated in model validation framework to represent their influence on actual system in real test environment. Thus, the modeling errors can be commonly shared by uncertainty and disturbance and noise. Model validation should exclude the influence of disturbance and noise as much as possible and identify the uncertainty magnitudes correctly. The consistency of the results of Case (a) and (b) demonstrates the validity of the presented method. It is seen that the presented model validation method can accurately estimate the components of the model errors that are contributed by uncertainty and the rest errors can be considered caused by disturbance and noise.
For Case (c), the influences of different uncertainty weighting proportions on the uncertainty magnitudes obtained by model validation and the subsequently predicted robust flutter speeds are studied and discussed. The proportional relations are set for both two types of aerodynamic uncertainty structures and the robust flutter speeds are also predicted respectively. The results are displayed in the following table, where denotes the robust flutter speed and the unit is m/s.
Table 2The comparison of robust flutter speed for different weighting designs
1) 2:1:1:1 / 2:1:1 | 0.0404/0.0457 | 158.7/159.5 |
2) 3:1:1:1 / 3:1:1 | 0.0497/0.0406 | 158.5/159.7 |
3) 1:3:1:1 / 1:3:1 | 0.0217/0.0215 | 157.5/158.5 |
4) 2:1:4:4 / 2:1:8 | 0.0286/0.0240 | 153.0/154.5 |
Comparing the results of the two structure types of aerodynamic uncertainty shown in Table 2, it is seen that aerodynamic uncertainty of parametric form produces little more conservative results, while the unmodeled dynamics descriptions which are expressed by full complex blocks reduce the conservatism of the predicted results. Although the parametric aerodynamic uncertainty represented by repeated scalar blocks could reflect the contribution of modal aerodynamics to the uncertainties and gives a specific physical meaning, the uncertainty structure is fixed, which will lead to a strong constraint for the optimization process. On the other hand, the form of full complex blocks relaxes the constraints on the structure of uncertainty, which will reduce the conservatism of the predicted results.
The weighting proportion also affects the predicted robust flutter speed. Proportional relationship (1) could reflect the prior information accurately, since the proportion is set according to the deviations of the stiffness and damping of the nominal model from the “known actual system”. Therefore, the corresponding results are relatively close to the real flutter speed. Proportional relationship (2) increases the magnitude of damping uncertainty and decreases the magnitudes of stiffness and aerodynamic uncertainties. These variations have a small effect on the predicted robust flutter speed. The results demonstrate that the structural damping has no remarkable influence on flutter speed which is considered as a regular phenomenon and a basic conclusion in aeroelasticity. Proportional relationship (3) and (4) increase the magnitudes of stiffness and aerodynamic uncertainties respectively, and the results indicate that the primary factors that significantly affect the flutter speed are stiffness and aerodynamic uncertainties, especially the aerodynamic uncertainty.
Apparently, if the weighting proportion between the uncertainties is set unreasonable, the predicted results will be excessively conservative. Although it is guaranteed that the actual system can be included in the aeroelastic model set, the prediction will be meaningless. Thus, it is concluded that the prior information about uncertainty, the actual system and the test condition and environment is very important, which can provide the mechanism of uncertainty, influence of various uncertainty on flutter speed and the initial guesses of uncertainty magnitude. Since aerodynamic forces and stiffness have a remarkable influence on flutter speed, it is desired that the magnitudes of aerodynamic and stiffness uncertainties be as small as possible. So the corresponding weighting proportion should be assigned relatively lower. On the other hand, in order to obtain a less conservative prediction, the model errors should be assigned to damping uncertainty as much as possible, which is less sensitive to flutter speed. It is seen from Table 2 that the assignment and trade-off of weighting proportion is of great influences on the final model validation results and robust flutter predictions. How to determine the weighting proportion and subsequently reduce the conservatism of the prediction is a crucial problem of model validation and is worthy of further study.
4.2. Fuselage-wing-store model
In aircraft structure design, the configuration that suspends the external stores, such as missiles and auxiliary fuel tank under the wing is very common. It is well known that the addition and/or modification of external equipment and stores on the aircraft deeply impact its aeroelastic characteristics, which are not fully predictable using linear flutter engineering tools and require flight test to produce a safety operational flight envelope with confidence. The influence of the store on aircraft structure is obvious, which causes dramatic parameter changes of the entire fuselage-wing-store structure. As for aerodynamics, although the wing provides major lifting forces for an aircraft and the stores commonly have slender configuration which does not provide lifting forces directly, the aerodynamic interferences among every aircraft component indeed affect the aerodynamic forces and the flow field. Therefore, the significant influence of fuselage-wing-store aerodynamic interferences on the flutter speed can’t be neglected. This effect proposes challenges for unsteady aerodynamics calculation and flutter analysis. The modeling of external store aerodynamics precisely and concisely is difficult, so it is desirable and reasonable to consider these aerodynamic interferences as aerodynamic uncertainties for robust flutter analysis.
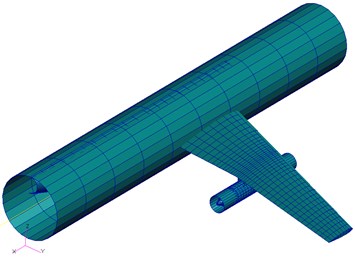
As the geometry is assumed symmetrical, the finite element model of a half of the aircraft with external store for calculating normal modes using MSC/NASTRAN is shown in Fig. 5. The flutter characteristics of the fuselage-wing-store structure with/without aerodynamic interference effects are compared and the influences of aerodynamic interference on aerodynamic forces and flutter speed are discussed. It is assumed that, the aerodynamic influence matrix without interferences is the nominal matrix and the aerodynamic influence matrix of the entire model considering store and fuselage aerodynamic interferences is the true plant matrix. The variations of aerodynamic matrix due to the influences of slender bodies are considered to be unmodeled dynamics with full complex blocks structure. The numerical example established a finite element model of a half simplified aircraft with one external store. The actual system, nominal system and uncertainty description are designed and the input and output signals are simulated as testing data to perform model validation. Robust stability of the uncertain aeroelastic system is analyzed via theory of structured singular value and the robust flutter speed is obtained.
The aerodynamic interference model is shown as Fig. 6. The flow field of the fuselage-wing-store model is treated as laminar flow, implying that flow is attached to the solid wall at all times and no separation is observed. Since the flow velocity is in subsonic regime, shock wave would not appear or is so weak that can be neglected. The unsteady aerodynamic forces of the wing without aerodynamic interferences are computed by doubletlattice method, while the fuselage-wing-store aerodynamic interferences have influences on the flutter speed. To account for this effect, the global fuselage-wing-store aerodynamic forces are computed via subsonic wing-slender interference theory [31], which idealizes bodies (i. e. fuselage and store) as “slender” and “interference” elements in combination. The primary purpose of the slender body elements is to account for the forces arising from the motion of the body, whereas the interference elements are used to account for the interference among all bodies and panels in the same group. This is implemented by providing a surface through which the corresponding boundary conditions are imposed. The aerodynamic interference effects are reflected in the obtained AIC matrices.
Fig. 5The finite element model of fuselage-wing-store model

Fig. 6The fuselage-wing-store aerodynamic interferences model
The first five order structural modal parameters and mode shapes and aerodynamic influence coefficient matrices are calculated and exported. Table 3 shows the natural frequencies and Fig. 7 displays the mode shapes. The modal mass , stiffness , damping , generalized AIC matrix and mode shape vectors are all obtained. Note that, denotes the generalized AIC matrices with the aerodynamic interferences effects of fuselage and store. The parameters of actual system are set as , , , and the nominal model are designed as , , , , where is chosen as the generalized AIC matrix without considering the interferences of store and fuselage. This design means that the structures of actual system and nominal model are the same, whereas the only differences are aerodynamics with/without interferences of fuselage and store. That is to say only uncertainties of unsteady aerodynamic forces are considered. The flutter speeds of actual system and nominal model for sea level are computed by state-space method and the results are and respectively.
Table 3Natural frequency of fuselage-wing-store model
Mode shape | First bending | Second bending | First torsion | First lag | Third bending |
Natural frequency (Hz) | 3.496 | 12.274 | 19.944 | 22.372 | 27.274 |
Excitation signals with exogenous disturbance are applied to the structure and the aeroelastic responses are simulated in noise environment. Both the input and obtained output data are considered as the testing measured data and used for model validation. The aerodynamic uncertainty is modeled according to section 2.2 and the model validation framework of uncertain aeroelastic system is formulated. Since previous numerical example has demonstrated that the model validation method presented in this paper could effectively eliminate the influence of disturbance and noise on the identification of the uncertainty magnitudes, the exogenous disturbance and noise are introduced to simulate the real testing environment and share the modeling errors with uncertainty. The identified aerodynamic uncertainty magnitude is optimized as and the robust flutter speed of the fuselage-wing-store model with an aerodynamic uncertainty is which is predicted according to the model validation result. The values for three different flow velocities are shown in Fig. 8.
Fig. 7The mode shapes of the fuselage-wing-store model

(a)
(b)
(c)

(d)
(e)
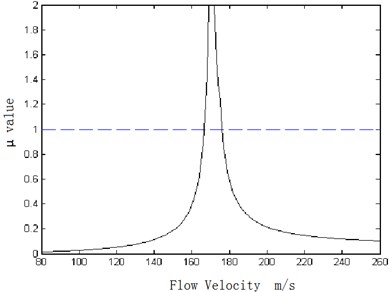
Fig. 9 displays the maximum values of fuselage-wing-store model for a set of values of flow velocities. When the value of flow velocity is lower than the nominal flutter speed, the airspeed associated with 1 is the flutter speed of the worst-case, i. e. robust flutter speed. This speed can also be considered as the lower bound of the flutter speed , while the airspeed corresponding to another intersection point of 1 is defined as the upper bound of the flutter speed . The characteristics of - curve are discussed in detail in [33-34]. The flutter speeds of the model set are bounded between and , so if the model validation is performed effectively, the real or experimental flutter speed lies within that bound. The lower and upper bounds of flutter speed are and . The result indicates that the flutter speed of “actual system” is included in the interval of the bounds, which demonstrates the model validation is effective and the robust flutter prediction is meaningful. Note that the upper bound is very close to the real flutter speed. This closeness indicates that the validation process produces a result with less conservatism. Furthermore, it is found that both lower bound and upper bound provide useful or even important information. To locate the real flutter speed precisely, the interval of bound should be as narrow as possible, which depends on a less conservative result provided by model validation.
Fig. 8The μ value curves of fuselage-wing-store model with aerodynamic uncertainty
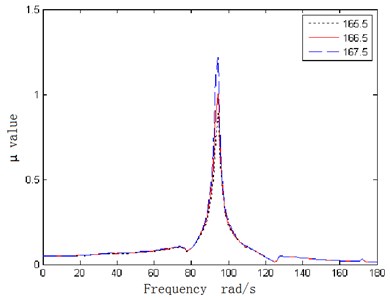
Fig. 9The V-μ curve of fuselage-wing-store model with aerodynamic uncertainty
For aircraft with stores, the aerodynamic interferences of store, the stiffness of pylon between aircraft and store, the span location of store and the variation of mass and gravity center all have certain influences on the flutter characteristics of aircraft. The presented example only considers the influences of the aerodynamic interferences induced by slender bodies of fuselage and store. The interferences of slender bodies on panel aerodynamics are set as unmodeled dynamics and the corresponding uncertainty magnitude is estimated by the model validation procedures presented in this paper. It is observed from the model validation result and the robust flutter prediction that the fuselage-wing-store aerodynamic interferences can be identified as an uncertainty and this manner of treatment is reasonable. Therefore, the influences of fuselage-wing-store aerodynamic interferences on flutter characteristics should be considered as an important factor in flutter analysis.
5. Conclusion
This paper deals with the problems of model validation and robust flutter analysis of uncertain aeroelastic system. The structures of uncertainties are designed and represented as parametric form and unmodeled dynamics. An LFT model validation framework of the uncertain aeroelastic system is established to identify the model validating uncertainty set. Based on Nevanlinna-Pick matrix interpolation theory, a test condition for validity of the uncertain aeroelastic model is developed and applied to estimate the uncertainty magnitudes by an optimization process. Finally, the robust flutter speeds are predicted according to the obtained model validating uncertainty set. Two numerical examples are presented of which the simulation results demonstrate the validity of the developed method. The results of straight wing model with structural and aerodynamic uncertainties suggest that:
(1) The influences of exogenous disturbances and noise, which are inevitable in actual testing environment, have to be included in model validation framework to reduce the conservatism of the uncertainty bounds;
(2) The proportion relationship among the uncertainty weightings is crucial to the model validation and should be designed reasonably by analyzing the prior information;
(3) In practical application, prior information of the actual system, which could helpful to determine the source and structure of the uncertainty, should be acquired before model validation, such as the essential characteristics of the system, the interaction mechanism of uncertainty and statistical properties of exogenous disturbance and environmental noise, etc.
The results of fuselage-wing-store model indicate that:
(1) The aerodynamic interference effects should be considered as an important influencing factor in flutter analysis;
(2) The aerodynamic interferences can be identified as an uncertainty and the predicted lower and upper bounds include the actual flutter speed with small conservatism, which could demonstrate the rationality of this manner of treatment.
The model validation method presented in this study could provide a reasonable uncertainty magnitude with less conservatism for robust flutter analysis. Nevertheless, for practical application, several problems need to be solved, such as how to obtain the prior information, the mechanism of uncertainty, the sources and effective structure of uncertainty and improved magnitude estimation procedures, etc. Therefore, uncertainty modeling and model validation are the crucial part for robust flutter prediction, which still need further study for real flight test application.
References
-
Kimberlin R. D. Flight testing of fixed-wing aircraft. AIAA Education Series, 2003.
-
Silva W., Brenner M., Cooper J., et al. Advanced Flutter and LCO Prediction Tools for Flight Test Risk and Cost Reduction – an International Collaborative Program for T&E Support. AIAA-2005-7630, 2005.
-
Lind R., Brenner M. Robust Aeroservoelastic Stability Analysis. Springer, London, 1999.
-
Lind R., Brenner M. Robust Flutter Margin Analysis that Incorporates Flight Data. NASA/TP-1998-206543, 1998.
-
Lind R., Voracek D. F., Truax R., et al. A flight test to demonstrate flutter and evaluate the flutterometer. The Aeronautical Journal, Vol. 10, 2003, p. 577-587.
-
Pettit C. L. Uncertainty quantification in aeroelasticity: recent results and research challenges. Journal of Aircraft, Vol. 41, Issue 5, 2004, p. 1217-1229.
-
Borglund D., Ringertz U. Efficient computation of robust flutter boundaries using the μ-k method. Journal of Aircraft, Vol. 43, Issue 6, 2006, p. 1763-1769.
-
Brenner M. J. Aeroservoelastic model uncertainty bound estimation from flight data. Journal of Guidance, Control and Dynamics, Vol. 25, Issue 4, 2002, p. 748-754.
-
Smith R. S., Doyle J. C. Model validation: a connection between robust control and identification. IEEE Transactions on Automatic Control, Vol. 37, Issue 7, 1992, p. 942-952.
-
Jie Chen, Shuning Wang Validation of linear fractional uncertain models: solution via matrix inequalities. IEEE Transactions on Automatic Control, Vol. 41, Issue 6, 1996, p. 844-849.
-
Jie Chen Frequency-domain test for validation of linear fractional uncertain models. IEEE Transactions on Automatic Control, Vol. 42, Issue 6, 1997, p. 748-760.
-
Demin Xu, Zhang Ren, Guoxiang Gu, Jie Chen LFT uncertain model validation with time- and frequency-domain measurements. IEEE Transactions on Automatic Control, Vol. 44, Issue 7, 1999, p. 1435-1441.
-
Lim K. B., Balas G. J., Anthony T. C. Minimum-norm model validating identification for robust control. AIAA, 1996, p. 96-3717.
-
Lim K. B., Giesy D. P. Computation of LFT uncertainty bounds with repeated parametric uncertainties. Proceedings of the American Controls conference, American Automatic Control Council, Evanston, IL, 1998, p. 1018-1022.
-
Kumar A., Balas G. J. An approach to model validation in the μ framework. Proceedings of the American Control Conference, Baltimore, USA, 1994.
-
Borglund D. The μ-k method for robust flutter solution. Journal of Aircraft, Vol. 41, Issue 5, 2004, p. 1209-1216.
-
Lim K. B., Giesy D. P. Parameterization of model validating sets for uncertainty bound optimizations. Journal of Guidance, Control, and Dynamics, Vol. 23, Issue 2, 2000, p. 222-230.
-
Lim K. B., Giesy D. P. Structured uncertainty bound determination from data for control and performance validation. NASA/TM-2003-212441.
-
Danowsky B. P., Christos J. R., Klyde D. H., et al. Evaluation of aeroelastic uncertainty analysis methods. Journal of Aircraft, Vol. 47, Issue 4, 2010, p. 1266-1273.
-
Chan-gi Pak, Shun-fat Lung Flutter analysis of aerostructures test wing with test validated structural dynamic model. Journal of Aircraft, Vol. 48, Issue 4, 2011, p. 1263-1272.
-
Chan-gi Pak Unsteady aerodynamic model tuning for precise flutter prediction. Journal of Aircraft, Vol. 48, Issue 6, 2011, p. 2178-2184.
-
Leijonhufvud M. C., Karlsson A. Industrial application of robust aeroelastic analysis. Journal of Aircraft, Vol. 48, Issue 4, 2011, p. 1176-1183.
-
Riley M. E., Grandhi R. V., Kolonay R. Quantification of modeling uncertainty in aeroelastic analyses. Journal of Aircraft, Vol. 48, Issue 3, 2011, p. 866-873.
-
Poolla K., Khargonekar P., Tikku A., Krause J., Nagpal K. A time-domain approach to model validation. IEEE Transactions on Automatic Control, Vol. 39, Issue 5, 1994, p. 951-959.
-
MATLAB Optimization Toolbox User’s Guide. The Math Works Inc., 2010.
-
Albano E., Rodden W. P. A doublet-lattice method for calculating lift distributions on oscillating surfaces in subsonic flows. AIAA Journal, Vol. 7, Issue 2, 1969, p. 279-285.
-
MSC Nastran Aeroelastic Analysis User’s Guide. MSC Software Corporation, 2010.
-
ZAERO theoretical manual version 8.3. ZONA Technology Inc., 2008.
-
Roger K. L. Airplane math modeling methods for active control design. Proceedings of the 44th AGARD Structures and Materials Panel, CP-228, AGARD, 1977, p. 4.1-4.11.
-
Lind R. Match-point solution for robust flutter analysis. Journal of Aircraft, Vol. 39, Issue 1, 2002, p. 91-99.
-
MSC Quick Reference Guide. MSC Software Corporation, 2005.
-
Balas G. J., Doyle J. C., Glover K. MATLAB μ Analysis and Synthesis Toolbox User’s Guide. The Math Works Inc., 2001.
-
Borglund D. Upper-bound flutter speed estimation using the μ-k method. Journal of Aircraft. Vol. 42, Issue 2, 2005, p. 555-557.
-
Yun H. W., Han J. L. Robust flutter analysis of a nonlinear aeroelastic system with parametric uncertainties. Aerospace Science and Technology, Vol. 13, Issue 2-3, 2009, p. 139-149.
About this article
This work was funded by the Natural Science Foundation of China (Grant No. 11102085) and Research Fund for the Doctoral Program of Higher Education of China (20103218120002).
