Modeling and optimal design for the fixed plate of steel ball grinding machine

2.1. Displacement sensitivity analysis

The basic equation for static analysis of finite element method on the fixed plate structure is:

where $\left[K\right]$ is the structure overall stiffness matrix, $X$ is nodal displacement column vector, $F$ is nodal load column vector.

When external loads are unconcerned with design variable $Y$, the equation of (1) is differentiated with respect to $Y$, which can be represented as follows:

Let:

then:

2.2. Stress sensitivity analysis

When the unit node displacement is known, stress $\sigma =\left[D\right]\left[B\right]U^e$, the first derivative of $X_i$ can be obtained as follows:

where $\left[D\right]$ is elastic matrix of element material and only related to the elastic constants of material, $\left[B\right]$ is geometric matrix, $U^e$ is the unit node displacement.

2.3. Analysis settings

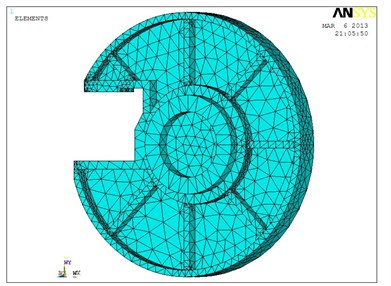
The structural model must be parameterized when the optimization module of ANSYS is used [5]. The fixed plate should be taken into consideration to establish analysis model directly in ANSYS, as shown in Figure 1. Firstly, the properties of material is defined: the material of the fixed plate is HT300, elastic modulus $E$ is 1.43×10¹¹ Pa, Poisson's ratio $\mu$ is 0.27, density $\rho$ is 7300 kg/m³, strength limit ${\sigma }_b$ is 3×10⁸ Pa. Secondly, the element type is defined. The structure of the fixed plate is complex and irregular shapes. Solid 92 in the software library of element type is selected as analyzed element. The structure of the element is a 3-dimensional, 10-node tetrahedral entity with a secondary displacement which is suitable for simulating the irregular meshes. This element is defined by 10 nodes, and each of which has 3 degrees of freedom, with properties as plasticity, swelling, stress stiffening, large deformation and large strain capacity. ANSYS meshing: the model in Figure 1 is divided intelligently into 123429 elements and 189701 nodes as in Figure 2. Finally, the boundary conditions and load cases are imposed. In practical work, the fixed plate is installed on the hydraulic cylinder, the displacement constraint is imposed on the direction which connecting the hydraulic cylinder. When the steel ball grinding machine is working, the fixed plate is steadily pressed by the rotating disc, the displacement constraint is imposed on the direction which is connecting grinding wheel.

Fig. 1The three-dimensional solid model of fixed plate

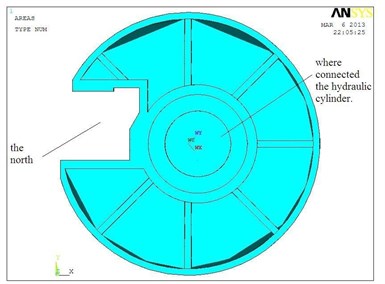
Fig. 2The finite element mesh distribution of fixed plate

2.4. The finite element analysis results of the fixed plate

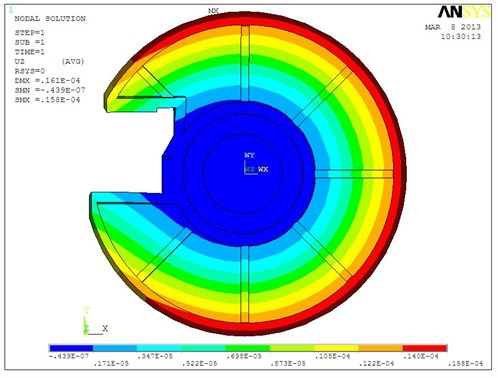
The overall deformation [6, 7] of the fixed plate is as in Figure 3, where the deformation of the fixed plate is gradually increased from the center outward and it is most obvious at the breach, with a maximum deformation of 2.16×10^-5 m.

The stress of fixed plate as in Figure 4 shows that the maximum equivalent stress occurs in the places which connects with the hydraulic cylinders and the maximum stress is 6.71×10⁶ Pa, less than the ultimate strength of the material.

Fig. 3The overall deformation of fixed plate

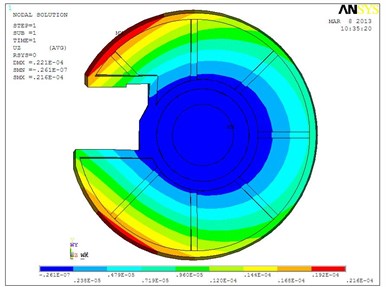
Fig. 4The stress map of fixed plate

3.1. Modal analysis theory and methods of computation

The motion equation of the damping vibration is from [8] as follows:

where $\left[M\right]$ is the mass matrix, $\left[C\right]$ is the damping matrix, $\left[K\right]$ is stiffness matrix, $\ddot{X}$ is acceleration vector, $\dot{X}$ is speed vector, $X$ is displacement vector, $F$ is excitation force vector.

In the case of the damping free vibration analysis of the multi-degree of freedom system, the motion equation is as follows:

Its corresponding characteristic equation is as follows:

where ${\omega }_i$ is the free vibration natural frequency, $X$ is free vibration mode shapes, which there are $N$ natural frequencies and mode shapes in the system with $N-$degree of freedom.

3.2. Loading and modal analysis results

Inherent characteristics are constituted by a set of modal parameters such as the natural frequency and vibration mode, which is determined by the structure itself such as distribution of mass and stiffness, and independent of the external load.

The natural frequencies of six modes are obtained by using ANSYS, which are shown in Table 1.

Fig. 5The first order mode

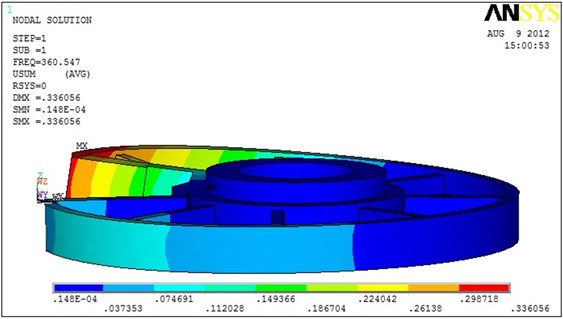
As in Table 1, the natural frequency is much larger than its operating frequency, so the resonance does not occur. As in Figure 5, the bending vibrations are in the axial of the fixed plate, which will reduce the service life of the fixed plate. What’s more, it will affect the stability and balls accuracy in the practical work. Therefore, the stiffness and damping of the structure must be added partially in designing the structure to suppress the effect of the vibration.

4.1. Grinding motion

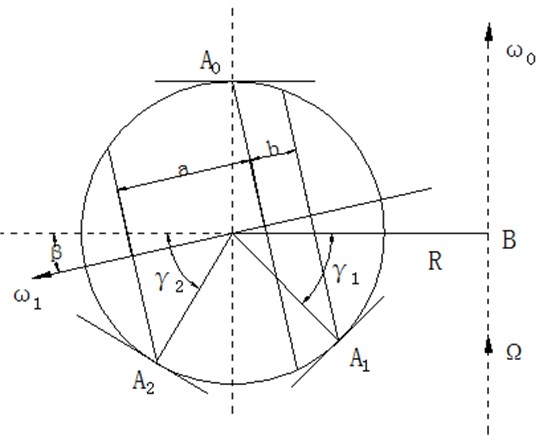
The steel ball is affected by three surfaces of the grinding disc. The touching surfaces are so small that they can be simplified into three touching points. By taking a steel ball as the research object, which radius is $r$, as in Figure 6, the three points are $A_0$, $A_1$ and $A_2$, and revolution angular velocity ${\omega }_0$ and rotation angular velocity ${\omega }_1$ coexist in the steel ball grinding movement, and the vector of ${\omega }_1$ exists in the cross section which contains $A_0$, $A_1$ and $A_2$.

Fig. 6Distribution of grinding trace

If $Q$ is grinding pressure of the fixed plate, $n$ is the total number of steel balls, $Q_0$ is the grinding pressure of a steel ball, which is grinding pressure of $A_0$ too. $N_1$ and $N_2$ are grinding pressure of $A_1$ and $A_2$. When ${\gamma }_0=$0, the dynamic relative relationship is approximated as:

4.2. Grinding pressure

According to the theory of elasticity, the contact deformation areas of the three points are elliptical. The steel ball radius is much smaller than the orbital radius, so the three elliptical regions are approximated as circles. Supposing the three radius of the circle regions are $r_0$, $r_1$, $r_2$. The modulus of the steel ball, the fixed plate and rotated plate are $E$, $E_0$, $E_1$ and which Poisson's ratios are $\upsilon$, ${\upsilon }_0$, ${\upsilon }_1$. Then the formulas [8] are as follows:

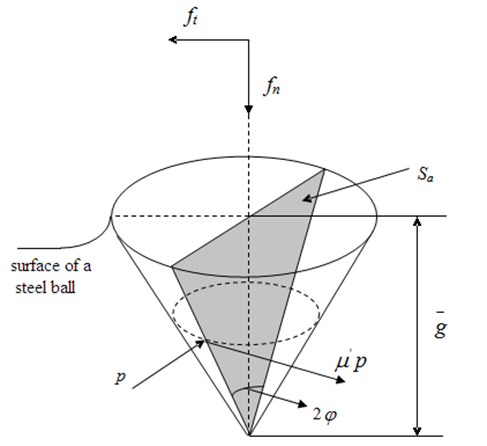
The shape of the abrasive grains are irregular. In order to get it analyzed, abrasive cutting edges are approximated as a conical which point angle is $2\varphi$, as in Figure 7. The cross-sectional area of actual cutting is $S_a$. The surface of the ball is protruded upward because of grinding. The working abrasive cutting edges is contacting with the steel ball with its front half. The pressure of touching surface is $p$, and the friction force of the steel ball is $\mu \text{'}p$. Then the tangential force $f_t$ and normal force $f_n$ are as follows [10]:

Fig. 7Grinding model of abrasive cutting edge

In its self-rotating circulation, the three points around the surface of the ball do the repeatedly grinding under the same circular trace. $N$ is the number of rotation laps. Supposing there is no slip grinding balls for motion and analyzing the grinding of $A_1$, it can be seen that if the grinding depth of the steel ball is $\text{Δ}\text{,}$ the grinding amount of a grinding cycle is $2r_1\text{Δ}2\pi \text{sin}({\gamma }_1+\beta )r$, the number of effective cutting is $2r_{1}2\pi \text{sin}({\gamma }_1+\beta )rjN$, where $j$ is the number of effective cutting in per unit area. If the length of the undeformed chip in the circle region is $r_1$, the section area of the undeformed chip is $\text{Δ}/r_{1}Nj$. Supposing the section modulus of the undeformed chip is $C$, the average abrasive cutting depth is $\overline{g}$ which satisfies the following relation as:

While the steel ball is grinded at $A_1$, the number of cutting is $r_1^{2}j\pi$. According to the formulas (16-18), the tangential force $f_t$ and normal force $f_n$ are obtained as follows:

Excluding the collision among the balls, let $f_n=N_1$, it can be obtained from the above equations as follows:

According to formula (21), if the steel ball, grinding discs and abrasive are ascertain, grinding pressure is determined by grinding depth, steel ball radius and orbital radius. Then the grinding surface pressure $P$ of the fixed plate can be determined, which provides theoretical support for the following parameter optimization design.

4.3. Structural optimization model

Because the notch of the fixed plate of steel ball grinding machine is the material inlet, the center of the ring circle which connected to the hydraulic cylinder is away $d=$0.3 m from the center of the fixed plate circle, against the notch. Which leads to the situation that the deformation of the fixed plate around the notch is the maximum and uneven which causes the unevenness and lower accuracy of the grinding steel balls. In the paper the structure of the fixed plate is improved to reduce the width of the notch in the case of the small impact of the amount of material, then by making the ring connected to hydraulic cylinder move to the notch as far as possible. The optimal offset can be found by the optimization design module of ANSYS [11]. The maximum amount of deformation must be minimized so that the deformation of the fixed plate can be more even. Meanwhile, reducing the notch appropriately will increase the local stiffness of the structure and reduce the vibration of the fixed plate.

Because the design variables can not be minus in ANSYS, when modeling the fixed plate, the abscissa $x$ of the center of the fixed plate is 0.4 m, the abscissa $x_1$ of the center of the ring circle is 0.4 m, the abscissa of polarized distance $d$ is $x_1-x$. Grinding surface is imposed pressure $P$. Because $x$ is a fixed value, $x_1$ is the design variables, and the maximum stress is state variables, which should be less than the ultimate strength of the material. The maximum amount of deformation of the fixed plate is the objective function. Then the structure optimization model is as follows [12]:

Objective function: $\text{min}f\left(X\right)=U_Z(x_1,x_2,...,x_n)$; $X=x_1$,

Design variables: 0.39$\le x_1\le$0.41,

State variables: $S_{MAX}\le \delta$,

where $U_Z$ is the maximum amount of deformation, $x_1$ is the abscissa of the center of the ring circle, the polarized distance $d$ is $x_1-x$. The lapping surface is imposed pressure $P$. If $d$ is minus, the ring is at left side. Strength of the material $\delta$ is 3×10⁸ Pa. The unit of the design variables and objective function is m, and the unit of state variables is Pa.

4.4. Analysis of optimization results

In the initial design, $x_1$ is 0.43 m, objective function $f\left(X\right)$ is 2.16×10^-5 m. As in Figure 8 and 9, after 15 iterations in the optimization process of ANSYS, the optimized design variables $x_1$ is 0.396 m and the objective function $f\left(X\right)$ is 1.575×10^-5 m. Compared with the original program the objective function is decreased by 27 %. As in Figure 10, the structural deformation of the fixed plate is more even.

Fig. 8Optimization process data

Fig. 9Optimization objective function graph

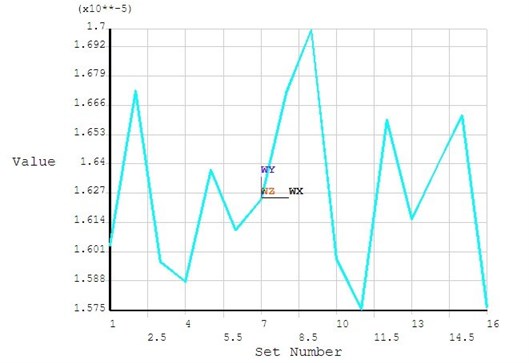
Fig. 10Optimized structural deformation