Free vibration analysis of suspended super long span CFRP cables

Wang, Libin; Guo, Xiaoyi; Noori, Mohammad; Feng, Dongming

Journal of Vibroengineering

Browse Journal

Submit article

Published: 31 December 2013

Check for updates

Free vibration analysis of suspended super long span CFRP cables

Libin Wang¹

Xiaoyi Guo²

Mohammad Noori³

Dongming Feng⁴

^{1, 2}School of Civil Engineering, Nanjing Forestry University, Nanjing, Jiangsu, 210037, China

³California Polytechnic State University, Mechanical Engineering Department, San Luis Obispo, CA 93407, USA

⁴Columbia University, Department of Civil Engineering and Engineering Mechanics, New York, NY 10027, USA

Corresponding Authors:

Libin Wang, Dongming Feng

Cite the article Download PDF

Downloads 1175

Abstract

The dynamic characteristics of an assumed isolated CFRP main cable are studied. The section area of the CFRP cable is determined for suspension bridge in different spans and sag-span ratios based on the principle of limit design at a given security coefficient. The Irvine parameter for suspension bridge with backstay and without backstay is calculated and a rule that Irvine parameter is linearly changed with span and sag ratio respectively is found. The analysis of frequency change with span shows that the first and third symmetric frequency is lager and less than the corresponding antisymmetric frequency respectively, but the second symmetric and antisymmetric frequencies are close to each other. The analysis on frequency and dimensionless frequency change with sag ratio show that for bridge with and without backstay the first and third order symmetric frequencies are larger and less than the corresponding antisymmetric frequencies respectively, but for a bridge without backstay the crossover phenomenon happens and the second symmetric mode changes from two to four internal nodes mode.

1. Introduction

Recently Carbon Fiber Reinforced Polymer (CFRP) has attracted growing interest as an alternative material to replace steel wires owing to its non-corrosiveness, very high strength, superior equivalent moduli, low expansion coefficient, outstanding fatigue behavior and light weight properties. The feasibility of the application of CFRP cable on extremely long-span bridge is being explored through experiment, theory, design and construction field [1-5].

Limited studies have been carried out on suspension bridges with CFRP main cables. A superiority of CFRP main cable in super large-span suspension bridge with CFRP main cable under static and dynamic loading was reported by Lijuan Li (2010), Cui-Juan Li (2011) and Yang Li (2012) respectively [6-8]. In the aforementioned study a comparative analysis on the dynamic characteristics of a super large-span suspension bridge with CFRP main cable and with steel main cable was performed. A series of measures to improve the wind resistance performance were proposed by Yang Li and Ru-Cheng Xiao on the study of the static and flutter stability of CFRP main cable (2012) [9]. The feasibility of CFRP main cable was also investigated to assess the wind resisting stability by Xin-Jun Zhang (2007) [10-11]. Based on these findings, a super long suspension bridge will be built one day in the future as many CFRP cable stayed bridges have been built in world-wide range [10-11]. Unfortunately, all literature reported on this subject is confined to the study of already constructed bridges [12-13]. To the best of the author’s knowledge, there is no report on the dynamic characteristics of suspended cable during the erection period.

The cable erection is an important construction phase in which the dynamic characteristics of the cable is a serious concern. Therefore, based on the linear vibration theory [14], a free vibration analysis of a flat suspended cable is presented in this paper. In order to lay the preliminary foundation for mastering the vibration characteristics of CFRP main cable during the cable erection construction, it is important to study the free vibration performance of CFRP cables.

2. Free vibration of a suspended cable

2.1. Assumptions for suspension bridge models

The main CFRP cables from two types of suspension bridge models (a) and (b) are shown in Fig. 1. The difference between these is whether to consider the unloaded backstays or not. All the cables are assumed to be uniform and elastic, and no bending stiffness is considered. The static sag is considered to be sufficiently small so that the mass of the cable per unit span can be taken as a constant. The hangers are assumed to be massless, inextensible and vertical, and are modeled as continuously and uniformly distributed along the span of the bridge. The initial uniform dead load on the girder is carried by the main cable without causing any stress in the stiffening girder. Under these assumptions the main cable adopts a parabolic profile under the initial dead load [15].

Fig. 1Two kinds of suspension bridge

a)

b)

2.2. In-plane vertical free vibration equation

Based on the assumptions established above, the equation of motion for the vertical free vibration is:

1

H \frac{\partial^{2} w}{{\partial x}^{2}} + h \frac{d^{2} z}{{d x}^{2}} = m \frac{\partial^{2} w}{{\partial t}^{2}},

in which $w (x, t)$ is the vertical displacement measured from the static configuration which is a function of the position $x$ and time $t$ . $H$ is the horizontal component of the cable tension, $h$ is the increment in the horizontal component of cable tension, $m$ is the total mass of the cable per unit length along the span. The dead-load parabolic profile $z (x) = 4 f x (L - x) / L^{2}$ is given in terms of the static sag $f = m g L^{2} / (8 H)$ .

To complete the formulation of the problem in terms of the two unknowns $w (x, t)$ and $h$ , it is necessary to introduce the compatibility condition affecting the longitudinal displacement of the cable. The linearized form of this condition for a single-span bridge of length $L$ is:

2

\frac{h L_{e}}{E A} = \frac{m g}{H} \int_{0}^{L} w d x,

where $E$ is the Young’s modulus of elasticity and $A$ is the cross-section area. For the CFRP cable from type (a) model, as described earlier, the formula for $L_{e}$ is [15]:

3a

L_{e} = \int_{0}^{L} {(d s / d x)}^{3} d x \approx L [1 + 8 {(f / L)}^{2}] .

And for the type (b) model, the formula for $L_{e}$ is [15]:

3b

L_{e} \approx L [1 + 8 {(f / L)}^{2}] + \frac{2 l}{\cos^{3} β},

where the $L$ is the horizontal projection of the backstays and $β$ is the angle between the backstays and the horizontal axis.

From equation (2) it is seen that $h = 0$ when $\int_{0}^{L} w (x, t) d x = 0$ . Modes that meet this condition and induce no additional tension may be called anti-symmetric. The other modes inducing an overall additional tension are symmetric.

2.3. In-plane antisymmetric modes

In the case of anti-symmetric in-plane modes, a simple analytical solution of Eq. (1) can be obtained in the form $w (x, t) = \tilde{w} (x) e^{i ω t},$ where $\tilde{w} (x)$ satisfies the differential equation:

4

H \frac{\partial^{2} \tilde{w}}{{\partial x}^{2}} + m ω^{2} \tilde{w} = 0 .

Together with the boundary conditions $\tilde{w} (0) = \tilde{w} (L / 2) = 0$ , the natural frequencies and mode shapes are given, respectively, by:

5

{\tilde{w}}_{n} = A_{n} \sin (2 n π x / L),

and:

6

ω_{n} = 2 n π {(H / m L^{2})}^{1 / 2},

where $0 < x < L, A_{n}$ is the amplitude of the vertical component of the antisymmetric mode, $n = 1,2, 3, \dots$ signify natural frequencies of the first, second, third modes, and so on.

Introducing $\bar{x} = x / L,$ $\bar{ω} = ω L / {(H / m)}^{1 / 2}$ into equation (6), the simple dimensionless formula is obtained as:

7

{\bar{ω}}_{n} = 2 n π .

2.4. In-plane symmetric modes

In case of symmetric mode $h \neq 0$ , let $h (x, t) = \tilde{h} (x) e^{i ω t} \neq 0$ , Eq. (1) then becomes:

8

H \frac{\partial^{2} \tilde{w}}{{\partial x}^{2}} + m ω^{2} \tilde{w} = \frac{m g}{H} \tilde{h} .

Given $\bar{\tilde{h}} = \tilde{h} / H$ , $\bar{\tilde{w}} = \tilde{w} / (m g L^{2} / H)$ , leads to the dimensionless equation ${\bar{\tilde{w}}}^{''} + {\bar{ω}}^{2} \bar{\tilde{w}} = \bar{\tilde{h}}$ . With the corresponding solution $\bar{\tilde{w}} = A \sin (\bar{ω} \bar{x}) + B c o s (\bar{ω} \bar{x}) + \bar{\tilde{h}} / {\bar{ω}}^{2}$ and the boundary conditions $\tilde{w} (0) = \tilde{w} (L) = 0$ , the final solution is:

9

\bar{\tilde{w}} = \frac{\bar{\tilde{h}}}{{\bar{ω}}^{2}} (1 - \tan (\bar{ω} / 2) \sin \bar{ω} \bar{x} - \cos \bar{ω} \bar{x}) .

From Eq. (9) and dimensionless Eq. (2), if we eliminate $\bar{\tilde{h}}$ we can obtain the following transcendental equation from which the natural frequencies of the symmetric in-plane modes may be found [14]:

10

\tan \frac{\bar{ω}}{2} = \frac{\bar{ω}}{2} - \frac{4}{λ^{2}} {(\frac{\bar{ω}}{2})}^{3},

in which the independent parameter called Irvine parameter is given by:

11

λ^{2} = {(m g L / H)}^{2} L / (H L_{e} / (E A)) .

3. Parameters of CFRP cables on suspension bridges

3.1. Material parameters and loadings

An example of a six-lane single-span highway suspension bridge is used to study the vibration frequency characteristics by changing its span and sag of the main cable. The modulus of elasticity of the CFRP is 165 GPa, the ultimate strength is 2000 MPa and the self-weight is 17.65 kN/m³. The uniform dead load of stiffening girder is 220 kN/m and the live load is 37 kN/m.

3.2. Section area determination

The section area of main cable is closely associated with the tensile strength of material, the deflection of cable, the span and the sag-span ratio of suspension bridge. Meanwhile the uniform dead load of main cable is also determined by the section area, so that the cross-sectional area is an important basic parameter of frequency of suspended cable.

According to references [6-9], the security coefficient of CFRP main cable is set as 3.0 based on the principle of limit design. Thus the section area is 0.493, 1.021, 1.588, 2.200, 2.857, 3.207, 3.576, 4.343, 5.188, 6.110 and 7.125 m²for each cable from 1000 to 10000 m span at 1000 increment in length of span, this group of data will be used to study the frequency characteristics of cable with span. The section area is 1.580, 1.885, 2.050, 2.230, 2.630, 3.100 m² at sag ratio 1/8, 1/9, 1/9.5, 1/10, 1/11, 1/12 respectively at a 3000 m long span cable, this group of data will be used to study the characteristic of natural frequency of cable with sag-ratio.

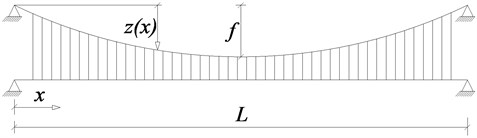
Fig. 2The change of parameter λ2 of CFRP cable with the span L

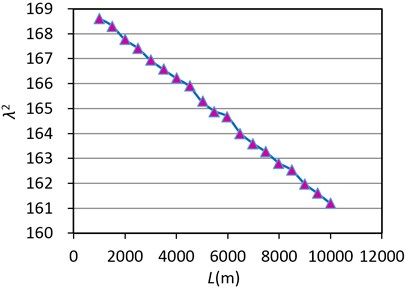
Fig. 3The change of parameter λ2 of CFRP cable with the sag-span ratio

4. Structural performance analysis

Using equation (10), the value of $λ^{2}$ for different span length and sag-ratio is calculated and shown in Figs. 2 and 3. Form Fig. 2 the range of $λ^{2}$ is 161~169, in which $λ^{2}$ is approximately linearly decreasing with the span increasing. Form Fig. 3 the range of $λ^{2}$ is 118~252, in which $λ^{2}$ is linearly increasing with the span increasing. It is obvious that the influence by sag ratio on $λ^{2}$ is greater than that by span.

4.1. Frequency variation of CFRP cable due to span change

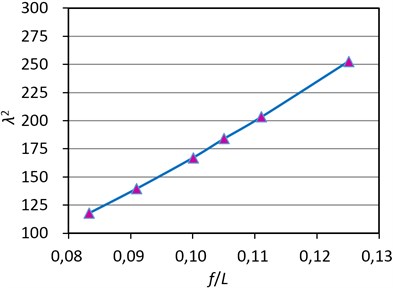
If we substitute $λ^{2}$ into equation (10) and equation (6) it will result in the symmetric and anti-symmetric frequencies of the CFRP cable. As Fig. 4 shows, the frequencies of anti-symmetric and symmetric in-plane modes are all decreasing with the increase of span and especially a rapid decrease happens from 1000 m to 3000 m long span cables. The first frequency of anti-symmetric mode is obviously less than the first frequency of symmetric mode, but the third frequency of anti-symmetric mode is larger than the third frequency of symmetric mode. The second frequency of anti-symmetric mode curve is very close to the second frequency of symmetric mode curve. It is seen that the frequency of symmetric mode of CFRP cable transforms from larger than the anti-symmetric mode to smaller than the symmetric mode.

With the backstays considered as in bridge model (b), $λ^{2}$ is almost a constant value of 96, which represents a lower cable stiffness, but the frequency variation rules are similar to the model (a).

4.2. Frequency variation of CFRP cable due to sag-span ratio change

4.2.1. Frequency in different sag-ratios in a 3000 m span bridge

The frequencies of different sag-ratios in a 3000 m span bridge are also calculated and shown in Fig. 5. As seen in Fig. 5 the vertical free vibration frequencies are all decreasing with the increasing sag-span ratios, except that the second free vibration frequencies are increasing. Similar to Fig. 4 the first frequency of anti-symmetric mode is still obviously less than the first frequency of symmetric mode and the third frequency of anti-symmetric mode is significantly larger than the third frequency of symmetric mode. It is worth noting that between the variation of the second free vibration frequencies, the second frequency of symmetric mode is less than the second frequency of anti-symmetric mode for the range $f / L = 1 / 12 ~ 1 / 11$ and the second frequency of symmetric mode is more than the second frequency of anti-symmetric mode for the range $f / L = 1 / 10 ~ 1 / 8$ . It is critically important to point out that an intersection point of the vertical free vibration frequency curves of symmetric and anti-symmetric modes occurs in the range $f / L = 1 / 11 ~ 1 / 10 .$ This is a significant finding from this analysis. That point is indicating a sag-span ratio where the second frequency of symmetric mode is equal to the second frequency of anti-symmetric mode.

The frequency of the model (b) exhibits the same characteristics, only that there is no crossover between the second anti-symmetric and symmetric modes.

4.2.2. Dimensionless frequency

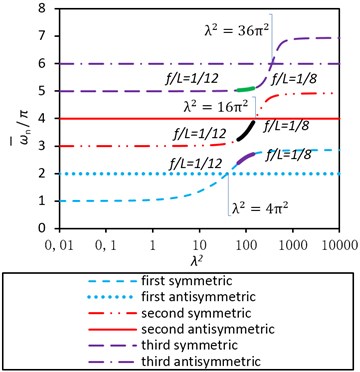
In Figs. 6 and 7 the plots of dimensionless frequency in terms of $λ^{2}$ for model (a) are presented, in which the horizontal line ${\bar{ω}}_{n} / π =$ 2, 4, 6 is corresponding to the first, second and third anti-symmetric modes respectively. The plots shown from the bottom to top are the first three symmetric frequencies. It is clear that there is a crossover point between the first three anti-symmetric and symmetric frequencies at $λ^{2} = 4 π^{2},$ $16 π^{2}$ and $32 π^{2}$ respectively. The phenomenon that the normalized dimensionless frequency of symmetric mode transcends anti-symmetric mode at one point is called the modal crossover.

The bold parts show the frequencies when the sag ratio ranges from 1/12 to 1/8. The special scope of $λ^{2}$ corresponding to the sag ratio range determines the characteristics of the vibration natural frequencies, that is the first symmetric frequency is less than the first anti-symmetric frequency, but the third anti-symmetric frequency is larger than symmetric frequency, and there is only one crossover point for second order frequency. On the left side of the point the anti-symmetric frequency is larger than symmetric and at the right part, it reverses.

For model (b) in Fig. 7, the scope of $λ^{2}$ moves slightly to the left compared to model (a), which leads to the fact that second and third anti-symmetric frequencies are larger than the symmetric frequency, but it is contrary for the first order frequency and there is no crossover point yet.

Fig. 4The change of frequency with the span L

Fig. 5The vertical bending natural frequency of CFRP cable of bridge (a) changes with the sag-span ratios (L= 3000 m)

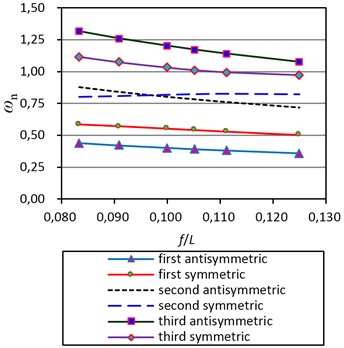
Fig. 6General dimensionless frequency curves of symmetric mode of CFRP cable of bridge (a)

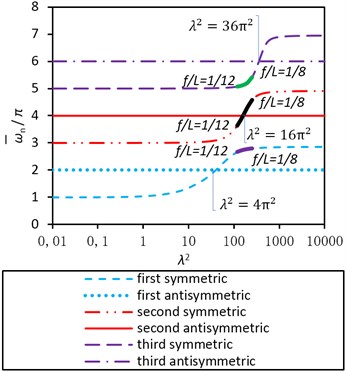
Fig. 7General dimensionless frequency curves of symmetric mode of CFRP cable of bridge (b)

5. Symmetric mode shapes

According to equation (9) the symmetric mode can be obtained for each order frequency of the CFRP cable. Herein only second symmetric mode is divided into three parts for the existence of crossover point $λ^{2} = 16 π^{2}$ in the range 118~252 as shown in Fig. 8 to Fig. 10.

Fig. 8The vertical component of the second symmetric in-plane mode 118<λ2<16π2

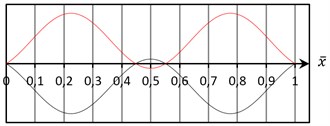
Fig. 9The vertical component of the second symmetric in-plane mode λ2=16π2

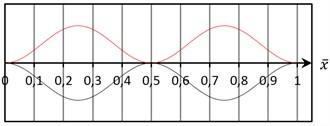
Fig. 10The vertical component of the second symmetric in-plane mode 16π2<λ2<252

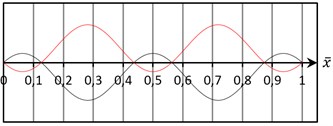
(a) For the case ${118 < λ}^{2} < 16 π^{2}$ , as Fig. 8 shows, the frequency of the second symmetric mode is less than the frequency of the second anti-symmetric mode. The vertical component of the second symmetric mode has two internal nodes along with the span. And the angular variation is appearing in supports.

(b) For the case $λ^{2} = 16 π^{2}$ which is the second modal crossover point, as Fig. 6 and Fig. 9 show, the frequencies of these modes are equal. The vertical modal component is tangential to the profile at the supports and mid-span.

(c) For the case ${16 π^{2} < λ}^{2} < 252$ , as Fig. 10 shows, the frequency of the second symmetric mode is larger than the frequency of the second anti-symmetric mode. Along with the span four internal nodes of the second symmetric mode appear at the supports and near the mid-span.

It is thus clear that the suspension bridge in the variation range of $λ^{2}$ has a modal crossover point $λ^{2} = 16 π^{2} .$ The interval is divided into two intervals by that point and it leads to the corresponding modal changes of CFRP cable from two internal nodes to four internal nodes.

The mode shapes and the corresponding eigenfrequencies results presented above are helpful for damage detection of the cables due to the fact that any damage will induce a change in eigenshapes and in the order of the frequencies or their magnitudes. Health monitoring of cables is always a major concern for the safety of the bridge.

Also the knowledge of free vibration of the suspended cable above is an essential prerequisite for a more in-depth understanding of the dynamic response of suspension cable under earthquake or wind excitation. A modal superposition method can always be used to determine the additional tension or deflection generated by the excitation. As our ongoing study shows the expression of participation factors $α_{n}$ and $β_{n}$ for additional tension and deflection are:

12

α_{n} = \frac{2 / 3}{[1 + λ^{2} {\{t a n ({\bar{ω}}_{n} / 2) / ({\bar{ω}}_{n} / 2)\}}^{2} / 12]},

13

β_{n} = \frac{α_{n}}{{\bar{ω}}_{n}^{2}} \{1 - \sec ({\bar{ω}}_{n} / 2)\} .

Both participation factors are expressed only in terms of ${\bar{ω}}_{n}$ and $λ^{2}$ , which were given in equations (10) and (11) respectively, thus the first several modes that participate most strongly in the generation of additional tension and deflection can be picked out in order and superposed to calculate the total extra tension or deflection, instead of superposing all modes together. Thus this will make tension calculation an easy task. Additionally, substituting equation (10) into (12), it is interesting that the extreme value of $α_{n}$ occurs when $λ^{2}$ is equal to 16 $π^{2},$ which is defined as the crossover point above. Other dynamic responses can also be further studied based on the results in this paper.

6. Conclusions

The sectional areas of two kinds of suspended cables in different spans and sag-span ratios are calculated according to the principle of limit design. Then the scope of the independent parameter $λ^{2}$ , which is the intrinsic (inherent) characteristic to determine the unique dynamic response of each type of CFRP cables, is obtained.

The study on the free vibration of the suspension cable through parameter $λ^{2}$ shows that the order and magnitude of the eigenfrequencies and the corresponding mode shapes will change if the modal crossover phenomenon happens with the variation of span or the ratio of sag to span of the bridge. The analysis discussed in this paper provides some basic aspects of the characteristics of free vibration of CFRP cable in isolated main cable erection phase. This finding is useful for modal measurement, parameter identification and damage detection of the CFRP cables. Also the results presented in this paper are the foundation for further study of the dynamic response to more complicated loadings such as earthquake or strong wind excitations.

References

Meier Urs. Carbon fiber-reinforced polymers: modern materials in bridge engineering. Structural Engineering International, Vol. 2, Issue 1, 1992, p. 7-12.

Search CrossRef
Meier Urs. Carbon fiber reinforced polymer cables: Why? Why not? What if? Arabian Journal for Science and Engineering, Vol. 37, Issue 2, 2012, p. 399-411.

Search CrossRef
Meier Urs. Connecting high-performance carbon-fiber-reinforced polymer cables of suspension and cable-stayed bridges through the use of gradient material. Journal of Computer-Aided Material Design, Vol. 3, Issue 1-3, 1996, p. 379-384.

Search CrossRef
Maeda Kenichi, Morizono Yasuyuki, Nakamura Hitoshi, Eguchi Tatsuya, Fujino Yozo. Applicability of CFRP cables to ultra long-span suspension bridges. Cable-Supported Bridges – Challenging Technical Limits, International Association for Bridge and Structural Engineering, IABSE Conference, Seoul, 2001, p. 83-90.

Search CrossRef
Xin Wang, Zhishen Wu. Integrated high-performance thousand metre scale cable-stayed bridge with hybrid FRP cables. Composites: Part B, Vol. 41, Issue 2, 2010, p. 166-175.

Search CrossRef
Lijuan Li, Hongyu Zheng, Huaiyan Jiang, Zhitao Lu. Natural vibration characteristics of long-span suspension bridge with CFRP cables. Advanced Material Research, Vol. 168-170, 2010, p. 1708-1711.

Search CrossRef
Cuijuan Li, Yuqiang Tong, Minghu Liu, Shizhong Qiang. Study on the rational structure system for super large-span suspension bridge with CFRP main cables. China Railway Science, Vol. 1, Issue 32, 2011, p. 62-66, (in Chinese).

Search CrossRef
Li Yang. Study on static mechanics of long span suspension bridge with CFRP cable. Journal of Chongqing University, Vol. 8, Issue 35, 2012, p. 26-33, (in Chinese).

Search CrossRef
Yang Li, Ru Cheng Xiao. Wind resistance performance of long-span suspension bridges with CFRP cables. Journal of Tongji University (Social Science Section), Vol. 4, Issue 40, 2012, (in Chinese).

Search CrossRef
Xinjun Zhang, Donglei Ying. Wind-resistant performance of cable-supported bridge using carbon fiber reinforced polymer cables. Wind and Structures, Vol. 2, Issue 10, 2007, p. 121.

Search CrossRef
Xinjun Zhang, Donglei Ying. Areodynamic stability of cable supported bridges using CFRP cables. Journal of Zhejiang University, Vol. 8, Issue 5, 2007, p. 693-698.

Search CrossRef
Y. L. Xu. Modal analysis of tower-cable system of Tsing Ma long suspension bridge. Engineering Structures, Vol. 19, Issue 10, 1997, p. 857-867.

Search CrossRef
J. M. Ko, S. D. Xue, Y. L. Xu. Modal analysis of suspension bridge deck units in erection stage. Engineering Structures, Vol. 20, Issue 12, 1998, p. 1102-1112.

Search CrossRef
Irvine H. M. Cable Structures. Dover Publications, New York, Massachusetts Institute of Technology Press, 1981.

Search CrossRef
J. Enrique Luco, Jose Trmo. Linear vertical vibrations of suspension bridges: a review of continuum models and some new results. Soil Dynamics and Earthquake Engineering, Vol. 30, Issue 9, 2010, p. 769-781.

Search CrossRef

About this article

Received

23 July 2013

Accepted

05 November 2013

Published

31 December 2013

Keywords

CFRP cable

span

sag-span ratio

parameter λ2

bridge vibration

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.