Abstract
A numerical model of rock fragmentation caused by a roadheader pick was established based on the particle flow code in two dimensions to study the rock fragmentation mechanism of the roadheader pick. The model simulated crack initiation, propagation and chip formation. The feasibility and reliability of the method as well as numerical model were verified by experiment. Results show that the rock fragmentation process includes three stages: crack initiation, crushing zone and radial crack formation, major tensile crack propagation and rock fragment formation. The crushing zone, number of radial cracks, specific energy consumption of rock cutting and dust level increase as the pick-tip corner radius increases. Consequently the pick-tip corner radius should range from 0 to 2 mm to obtain large rock fragments and low specific energy consumption. The damage of medium-hard and hard rock by the roadheader pick is more remarkable than that of soft rock. Furthermore, the sharp pick is suitable for the soft rock, whereas the pick tip with a proper rounding corner is perfect for the medium-hard and hard rock.
1. Introduction
Roadheader is widely used in rock cutting and is one of the key equipments for underground excavation [1, 2]. The roadheader pick plays a vital role when the roadheader works owing to its ability to cut rock directly. Thus studies on the rock fragmentation mechanism of the roadheader pick are particularly important. Many scholars have adopted various numerical simulation methods to study the rock fragmentation mechanism of a roadheader pick. Based on fracture mechanics theory and the maximum strain rate criterion, Hardy simulated fragment formation in the rock cutting process through the finite element method [3]. Ingraffea established a finite element model of rock cutting and used the maximum tensile stress criteria to analyze the formation of rock fragments [4]. Kou et al. used a two-dimensional (2D) RFPA program to simulate the fragmentation process of homogeneous rock [5]. Huang et al. took the 2D discrete element method to simulate the rock cutting mechanism and pointed out that the formation mechanism of the rock fragments is related to the cutting depth [6]. Rojek et al. adopted discrete element method in 2D and three-dimensional models to simulate the cutting force of the roadheader pick in the rock fragmentation process and compared the simulation results with experimental results [7]. Yu et al. used the explicit dynamic program LS-DYNA to simulate the rock fragmentation process with a rotary roadheader pick and pointed out that shear failure plays a dominant role in the rock failure [8]. Zhou et al. applied the LS-DYNA to study the effect of cutting angle on cutting force and specific energy consumption in the rock fragmentation process [9]. With regard to the cutting process and its influencing factors, numerous studies on metal cutting tools and TBM cutters exist [10-14], but only a few studies exist on roadheader picks. In particular, no study was carried out on the effect of the pick-tip corner radius and the rock property in the rock fragmentation process of the roadheader pick. Thus the numerical model of rock fragmentation of the roadheader pick was established based on the particle flow code in two dimensions (PFC2D). In this study the crack initiation and propagation in rock fragmentation process were simulated, and the effects of the pick-tip corner radius and the rock property on the rock fragmentation process were investigated.
2. Simulation method
2.1. Algorithm of the particle flow code
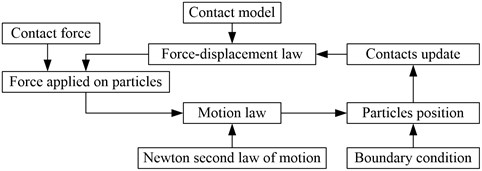
The PFC2D is developed based on explicit difference algorithm and discrete element theory. The basic mechanical properties of the medium are considered from the point of basic particle structure and are dependent on the contact status among those particles in different stress conditions [15]. Calculation theory of the particle flow code is based on the force-displacement law and Newton’s second law of motion. The contact force between particle and particle or wall is updated based on the force-displacement law. Motion law is used to update the particle position and generate new contacts among particles. The algorithm flow chart of particle flow code is shown in Fig. 1.
Fig. 1The algorithm flow chart of particle flow code
2.1.1. Force-displacement law
The force-displacement law derives the contact force acting on two entities in contact to the relative displacement between the particles. There are two contact forms, one is particle to particle and the other is particle to wall. For particle to particle contact, the contact force direction is directed along the line between particle centers, and the direction of contact force is directed along the line defining the shortest distance between the particle center and the wall at particle to wall contact. The contact force can be resolved into normal and shear components with respect to the contact plane as:
where is the contact force vector, represents the normal contact force vector, represents the tangential contact force vector.
For force-displacement law, a pair of springs is assumed to be acting on the contact point between particle and particle, the overlap can be regarded as the deformation of springs, normal contact force can be expressed as:
where is the normal contact stiffness, represents the normal overlap.
Similarly, the shear force acting on particle also follows the Hooke's law, the shear force increases with the relative shear displacement, it can be expressed as:
where is the shear force acting on particle, is the tangential contact stiffness.
2.1.2. Law of motion
Particle motion is caused by the contact force and moment acting on it, its motion can be described by Newton’s second law of motion, equations of motion can be expressed as:
where is the mass of particle, is the displacement of particle, is gravitational acceleration of particle, represents the moment vector acting on particle, is angular momentum of particle.
2.2. Contact bond model
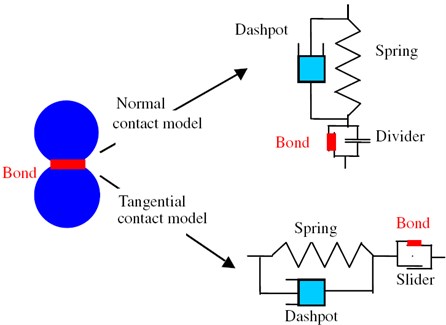
The bond should be set up between neighboring particles when the particle flow method is used to simulate the mechanical behavior of continuum material. With particle flow code in two dimensions (PFC2D), the contact bond model is offered to describe the mechanical effects at the contact of particles, which has been confirmed to simulate the macro-mechanical behavior of brittle material such as rock, concrete and so on. For this reason the contact bond model is adopted to describe the bond action among microcosmic particles and it is shown in Fig. 2. The contact bond can be envisioned as a pair of elastic springs (or a point of glue) with constant normal and shear stiffnesses acting at the contact point. And these two springs with specified shear and tensile normal strengths are used to represent normal bond strength and tangential bond strength.
Fig. 2Contact bond model
The relationships between normal contact force and normal relative displacement and between shear contact force and tangential relative displacement are shown Fig. 3. If the magnitude of the tensile normal contact force equals or exceeds the normal contact bond strength, the bond breaks and both the normal and shear contact forces are set to zero. If the magnitude of the shear contact force equals or exceeds the tangential contact bond strength, the bond breaks. The bond contact failure criterion can be expressed as:
where is normal contact bond strength, represents tangential contact bond strength.
When there is contact bond failure, a slip model is introduced to tangential contact model for simulating the frictional force between particles and the frictional force does not exceed the friction limit. It can be expressed as:
where is the frictional force between particles, is the friction coefficient between particles.
Fig. 3Mechanical performance of contact-bond model
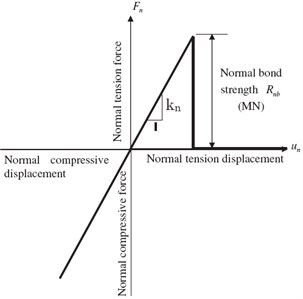
a) Normal contact model
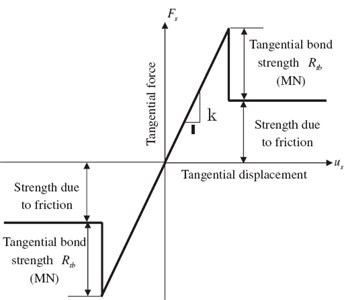
b) Tangential contact model
3. Establishing the numerical model of rock fragmentation
3.1. Simulation of rock specimen
A simulated rock specimen is necessary to be established and the microscopic parameters adjusted to make the mechanical properties of the simulation specimen compatible with the real rock specimen when the particle flow method is adopted to simulate the macroscopic mechanical behavior of the rock. The mechanical property parameters of the rock specimen (elastic modulus, Poisson’s ratio, uniaxial compressive strength and tensile strength) can be measured by simulating the uniaxial compression or by conducting Brazilian disc tests [12, 13]. The simulation process of the rock specimen is as follows: four walls, whose sizes are the same as the real rock specimen, are defined; the particle size is adjusted so the space formed by four walls is full of appropriate particles and the force between two particles decreases to a certain limit; the suspended particles are eliminated; the microscopic parameters and boundary conditions of particles are set. Next uniaxial compression tests of the rock specimen under different microscopic parameters are conducted and then the mechanical properties of the simulation specimen are considered to be the same as the actual rock when the stress-strain curves of the simulation and experiment agree. The results obtained using a set of microscopic parameters are shown in Fig. 4. The failure mode of the rock specimen is shown in Fig. 4(a). The simulation stress-strain curve is in accordance with the laboratory result shown in Fig. 4(b).
Five kinds of rocks with different mechanical properties are simulated by changing the microscopic parameters. Table 1 shows the microscopic parameters of simulation specimens, and Table 2 shows the macroscopic mechanical properties of simulation specimens.
Fig. 4Simulation of uniaxial compression test

a) Rock specimen of simulation test
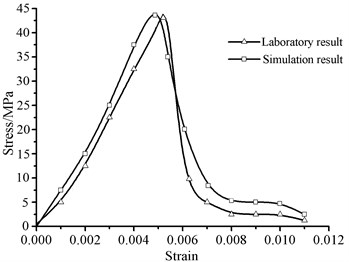
b) Stress-strain of simulation and experiment
Table 1Microscopic parameters of simulation specimens
No. | Friction coefficient | Contact stiffness (GN/m) | Stiffness ratio | Normal connection strength (MN) | Normal connection strength deviant (MN) | Tangential connection strength (MN) | Tangential connection strength deviant (MN) |
1 | 0.5 | 20.0 | 2.5 | 40.0 | 10.0 | 40.0 | 10.0 |
2 | 0.5 | 30.0 | 2.5 | 60.0 | 15.0 | 60.0 | 15.0 |
3 | 0.5 | 40.0 | 2.5 | 80.0 | 20.0 | 80.0 | 20.0 |
4 | 0.5 | 60.0 | 2.5 | 120.0 | 30.0 | 120.0 | 30.0 |
5 | 0.5 | 80.0 | 2.5 | 160.0 | 40.0 | 160.0 | 40.0 |
Table 2Mechanical parameters of simulation specimens
No. | Uniaxial compressive strength (MPa) | Tensile strength (MPa) | Modulus of elasticity (GPa) | Poisson’s ratio | Density (kg/m3) | Rock properties |
1 | 44.5 | 5.5 | 12.8 | 0.2 | 2700 | Soft rock |
2 | 67.4 | 7.85 | 19.8 | 0.2 | 2700 | Soft rock |
3 | 95.6 | 10.3 | 25.9 | 0.2 | 2700 | Medium-hard rock |
4 | 133.2 | 13.4 | 39.4 | 0.2 | 2700 | Medium-hard rock |
5 | 172.8 | 26.4 | 51.7 | 0.2 | 2700 | Hard rock |
3.2. Simplified simulation model
The carbide tip of the roadheader pick pushes into the rock and generates the crush zone and the radial crack when the cutting force is greater than the rock strength. Rock bearing forces come from three directions: the normal force caused by the sway of the roadheader cutting head, the cutting force caused by the revolution of the roadheader cutting head and the lateral force caused by the collision between the pick and the rock. This study finds that the formations of rock crushing, crack propagation and rock fragments are mainly the result of the cutting force. Thus the fragmentation process can be regarded as a plane problem to simulate the formations of rock crushing, crack propagation and rock fragments. Fig. 5 is the simplified plane model of rock fragmentation of the roadheader pick. Many scholars have used the 2D finite element method and the discrete element method to simulate the rock fragmentation process of the roadheader pick. For example Jonak et al. used the 2D finite element method to simulate the deformation of rock and formation of rock fragments during the rock fragmentation process of the roadheader pick and verified the correctness of their simulation results [16, 17]. Rojek et al. simulated the rock fragmentation process of the roadheader pick using the 2D discrete element method and the simulation’s cutting forces and size distribution of rock fragments were consistent with experiment [7].
Fig. 5Cutting parameters of rock fragmentation of the roadheader pick (h – cutting thickness, 15 mm; d – diameter, 20 mm; θ – cone angle of pick tip, 75°; γ – corner radius, mm; φ – impact angle, 40°; Fc – cutting force, N; Fn – normal push pressure, N)
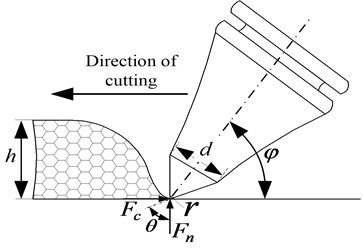
The carbide tip of the roadheader pick is usually made of high hardness carbide material. The stiffness and strength of the tip are very high. Thus the study regards the contour of the pick as the rigid wall and the rock specimen boundary conditions also apply as the rigid wall. The numerical model of the rock fragmentation process of the roadheader pick is shown in Fig. 6.
Fig. 6Numerical model of rock fragmentation of the roadheader pick

Fig. 7Simulation of rock fragmentation process by the roadheader pick
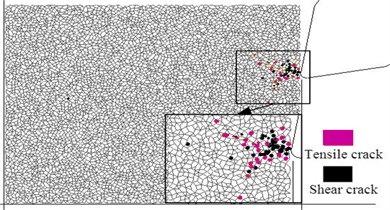
a) The initiation of micro cracks
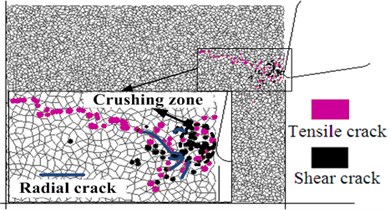
b) The formation of crushing zone and radial cracks
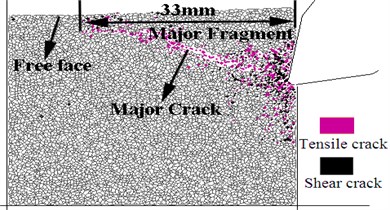
c) The growth of the major crack and formation of the cutting debris
4. Simulation analysis of rock fragmentation process
4.1. Process of crack propagation
Initiation of the microscopic tensile cracks and shear cracks in the rock fragmentation process can be effectively simulated by using the failure criteria of the connection between particles using the particle flow method. In this paper several codes were programmed with fish language to dynamically display the microscopic tensile cracks and shear cracks and to analyze the initiation as well as growth of cracks. During the simulation process the pick feed rate is 1 m/min and the rock is #5 simulated specimen. The rock fragmentation process of the roadheader pick is shown in Fig. 7, where the initiation, growth and entire process of cracks can be found directly. Initiation of the microscopic tensile cracks and shear cracks in the zone before the pick tip can be seen in Fig. 7(a), which shows the crack distribution within the rock when the penetration depth is 0.5 mm. Numerous cracks form in the crushing zone before the pick tip when the penetration depth reaches 1 mm. The distribution of microscopic tensile cracks and shear cracks in the crushing zone does not follow the obvious law as in Fig. 7(b) and many small radial cracks are found around the crushing zone because of its extrusion of crushing zone. The particles are assumed to be ideal rigid bodies in the particle flow method. The connection between the particles cannot be compressed to failure, but the compression may cause the tensile failure and shear failure between particles. Compression is the reason that the microscopic tensile cracks and shear cracks in the crushing zone have no obvious law. Radial cracks around the crushing zone propagate further when the penetration depth is 1.5 mm, as in Fig. 7(c). However, a few main cracks propagate to the rock-free surface when big rock fragments are formed. In addition, the major crack growth path is determined by the location of the rock-free surface and the shape of the crushing zone, whereas other cracks remain in the rock as the residual cracks. The growth of the major cracks is formed because of the confluence of many microscopic tensile cracks. This outcome shows that tension plays an important role in the formation of the main cutting debris and confirms the extrusion-tension theory of rock fragmentation using the roadheader pick [18]. The pick continues to penetrate the rock and forms new cutting debris by extrusion and tension effect. The rock fragmentation process of the roadheader pick will continue.
4.2. Experimental verification
The experiment of rock fragmentation was conducted on the linear cutting test bed to verify the correctness of the particle flow numerical model for rock fragmentation of the roadheader pick. The model’s experimental parameters are the same as the simulation parameters in Section 4.1. The test bed mainly includes rock specimen, guide rail, pick-holding device, pick and thrust oil cylinder as shown in Fig. 8. The cutting force variation of the two methods was compared in Fig. 9(a). Results show that the trends in cutting force variation of the experiment and numerical methods are consistent. The variations peaks then rapidly decrease and the penetration depths of the two peak cutting forces are consistent. However the values of the cutting force are different because the simulation is performed based on the PFC2D. The lengths of the rock fragments obtained through the experiment and the simulation method are 38 mm (Fig. 9(b)) and 33 mm (Fig. 7(c)) respectively. The result indicates that the crack growth path of the 2D plane conforms to the experiment, and the differences in values of the cutting force do not affect the study of the rock fragmentation mechanism and the cutting debris formation mechanism in the 2D model. Therefore the experiment results are consistent with the simulation results, and using the particle flow numerical model to study the rock fragmentation mechanism and the cutting debris formation mechanism is reliable and feasible. The model provides a reliable method to study the rock fragmentation mechanism, geometric parameters and cutting parameters of the roadheader pick.
Fig. 8Linear cutting test bed (1 – rock specimen, 2 – guide rail, 3 – pick holding device, 4 – pick, 5 – thrust oil cylinder)

Fig. 9Results of experiment and simulation
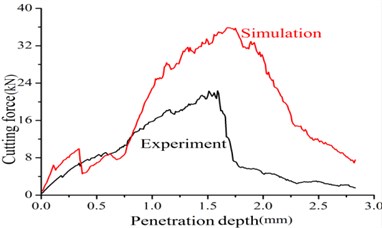
a) Cutting forces of experiment and simulation
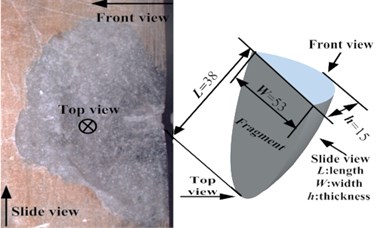
b) Rock debris avalanche shape
5. Influence of corner radius on the rock fragmentation process
The pick tip is usually properly rounded in the manufacturing process to improve the contact strength of the carbide tip and prolong the pick service life as much as possible [14]. The corner radius of the pick tip also enlarges often because of the wear in the rock fragmentation process, thus the rock fragmentation ability of the pick is severely affected. The rock fragmentation processes of different pick-tip corner radiuses (0, 1, 2 and 3 mm) were investigated. The pick penetration depth was 2 mm, the pick feed rate was 1 m/min and the rock was #5 simulated specimen. Rock fragmentations of the roadheader pick with different corner radiuses are compared in Fig. 10. The results show the following.
1. The size of the rounding corner has little effect on the rock fragmentation mechanism because the rock has the same cutting debris formation mechanism. First the pick pushes the rock and forms the crushing zone and radial cracks. Then the rock grains extrude the radial cracks to make them grow further. Lastly, the minority radial cracks expand to the rock-free surface and form rock fragments.
2. The crushing zone before the pick tip increases as the corner radius increases in the same penetration depth. The corner radius should not be too large and the pick wear should not be too serious in order to control the dust levels. Usually the corner radius is no more than 3 mm.
3. Radial cracks around the crushing zone are greatly influenced by the corner radius. The greater the corner radius, the more are the radial cracks and small cutting debris, but the smaller is the main rock fragment.
4. The corner radius has a great influence on the size of the main cutting debris. The smaller the corner radius, the greater are the main cutting debris. This influence is mainly because for the sharp pick tip it is easy to penetrate into the rock and it produces tensile force on the main cutting debris. Thus the corner radius should not be too large to obtain big rock fragments.
5. If the energy requirement for the formation of a microscopic tensile or shear crack is , then the specific energy consumption for the rock cutting (the energy consumed by the unit area of rock) can be expressed as follows:
where is the specific energy consumption for rock cutting, is the number of microscopic cracks and is the area of cutting rocks.
The specific energy consumption for rock cutting is greatly influenced by the corner radius as shown in Table 3. The sharper the pick tip, the smaller the specific energy consumption. The specific energy consumption quickly increases as the corner radius increases. However the pick tip cannot be made as an ideal cone and the pick wear happens in entire process. Thus the corner radius should be controlled from 0 mm to 2 mm when it is working.
Fig. 10Rock fragmentation process with different corners radiuses

a) 0 mm
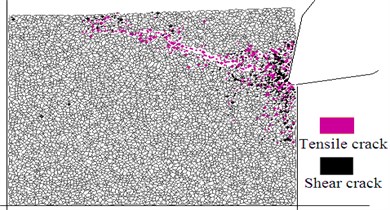
b)1 mm

c)2 mm
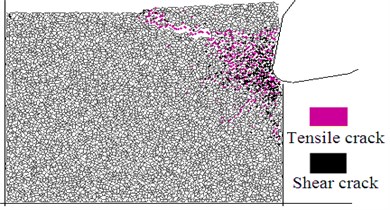
b) 3 mm
Fig. 11Simulation of rock fragmentation with different rock strengths

a) #1

b) #2

c) #3

d) #4

e) #5
Table 3Specific energy consumption with different pick-tip corner radius
(mm) | 0 | 1 | 2 | 3 |
571 | 484 | 839 | 701 | |
(mm2) | 58.3 | 30.5 | 38.9 | 21.3 |
(J/mm2) | 9.8 | 15.9 | 21.6 | 32.9 |
6. Influence of rock strength on the rock fragmentation process
Rock fragmentations of the roadheader pick with different rocks were carried out to study the influence of rock strength on the rock fragmentation process. The corner radius was 2 mm, the penetration depth was 2 mm and the pick feed rate is 1 m/min. The results are shown in Fig. 11.
1. The damage of the soft rock is less remarkable than of the medium-hard and hard rock. The forces on the soft rock are mainly the extrusion and the tension assisted, whereas the forces on the medium-hard and hard rock are mainly the tension and the extrusion assisted. The soft rock alleviates the force of the pick on the rock and limits the growth of radial cracks because of its small elastic modulus, small compressive strength and the weak bearing capacity of deformation. Although the medium-hard and hard rock are opposites, they need the roadheader pick to have sufficient stiffness and strength.
2. The crushing zone of the soft rock is bigger than of the medium hard and hard rock. The soft rock will produce considerable dust, increase the specific energy consumption and aggravate the pick wear. Thus the pick is not suitable for soft rock when the corner radius is more than 2 mm. The result confirms that the pick with suitable corner radius is appropriate for hard rock and the sharp pick is appropriate for soft rock.
7. Conclusions
1. The numerical model of rock fragmentation of the roadheader pick was established based on PFC2D and the study of the rock cutting process showed the following: the rock fragmentation process includes the crack initiation, crushing zone and radial crack formation, major tensile crack propagation and rock fragment formation. The study confirmed the extrusion-tension theory of rock fragmentation of the roadheader pick.
2. The experiment of rock fragmentation with the roadheader pick was done on the linear cutting test bed to verify the correctness of the particle flow numerical model of rock fragmentation. The experiment provides a reliable method to study the rock fragmentation mechanism, geometric parameters and cutting parameters of the roadheader pick.
3. The rock fragmentation processes of different pick-tip corner radiuses and rock properties were investigated. Results show that the crushing zone, the number of radial cracks and the specific energy consumption increase and the size of the cutting debris decreases as the corner radius increases. The corner radius should be controlled from 0 mm to 2 mm to obtain low specific energy consumption. The damage of soft rock is less remarkable than of the medium-hard and hard rock. Furthermore the pick with suitable corner radius is appropriate for hard rock, the sharp pick is appropriate for soft rock.
References
-
Balci C., Bilgin N. Correlative study of linear small and full-scale rock cutting tests to select mechanized excavation machines. International Journal of Rock Mechanics and Mining Sciences, Vol. 44, Issue 3, 2007, p. 468-476.
-
Bilgin N., Demircin M. A., Copur H., Balci C., Tuncdemir H., Akcim N. Dominant rock properties affecting the performance of conical picks and the comparison of some experimental and theoretical results. International Journal of Rock Mechanics and Mining Sciences, Vol. 43, Issue 1, 2006, p. 139-156.
-
Hardy M. P. Fracture Mechanics Applied to Rock. Ph. D. Thesis, University of Minnesota, Minnesota, USA, 1973.
-
Ingraffea A. R. Theory of crack initiation and propagation in rock. Atkinson B. (Ed.), Fracture Mechanics of Rock, Academic Press, Inc., Amsterdam, 1987.
-
Kou S. Q., Lindqvist P. A., Tang C. A., Xu X. H. Numerical simulation of the cutting of inhomogeneous rocks. International Journal of Rock Mechanics and Mining Sciences, Vol. 36, Issue 5, 1999, p. 711-717.
-
Huang H. Y., Detournay E., Belier B. Discrete element modeling of rock cutting. The 37th U. S. Symposium on Rock Mechanics (USRMS), Colorado, 1999, p. 123-130.
-
Rojek J., Onate E., Labra C., Kargl H. Discrete element simulation of rock cutting. International Journal of Rock Mechanics and Mining Sciences, Vol. 48, Issue 6, 2011, p. 996-1100.
-
Yu B., Khair A. W. Numerical modeling of rock ridge breakage in rotary cutting. ARMA General Meeting, Vancouver, 2007.
-
Zhou Y., Li G. S., Tang J. Y. Simulation and analysis for pick cutting rock by LS-DYNA. Journal of Engineering Design, Vol. 18, Issue 2, 2011, p. 103-108, (in Chinese).
-
Chen W. L., Liu N., Li W. 3D numerical simulation on metal cutting process. Transactions of the Chinese Society for Agriculture Machinery, Vol. 39, Issue 1, 2008, p. 151-155, (in Chinese).
-
Pan Y. Z., Ai X., Tang Z. T., Zhao J. Optimization of tool geometry and cutting parameters based on a predictive model of cutting force. China Mechanical Engineering, Vol. 19, Issue 4, 2008, p. 428-431, (in Chinese).
-
Su L. J., Sun J. S., Lu W. B. Research on numerical simulation of rock fragmentation by TBM cutters using particle flow method. Rock and Soil Mechanics, Vol. 30, Issue 9, 2009, p. 2823-2829, (in Chinese).
-
Sun J. S., Chen M., Chen B. G., Lu W. B., Zhou C. B. Numerical simulation of influence factors for rock fragmentation by TBM cutters. Rock and Soil Mechanics, Vol. 32, Issue 6, 2011, p. 1891-1897, (in Chinese).
-
Xia Y. M., Xue J., Zhou X. W. Rock fragmentation process and cutting characteristics on shield cutter. Journal of Central South University, Vol. 42, Issue 2, 2011, p. 954-959, (in Chinese).
-
Manual of Particle Flow Code in Two Dimensions. PFC2D Version 3.0, Minneapolis, Itasca Consulting Group Inc., 2002.
-
Jonak J., Podgorski J. Mathematical model and results of rock cutting modeling. Journal of Mining Science, Vol. 37, Issue 6, 2001, p. 615-618.
-
Jonak J. Influence of friction on the chip size in cutting the brittle materials. Journal of Mining Science, Vol. 37, Issue 4, 2001, p. 407-410.
-
Evans I. A theory of the picks cutting force for point-attack. Geotechnical and Geological Engineering, Vol. 2, Issue 1, 1984, p. 63-71.
About this article
The authors would like to acknowledge the Foundation of National 863 Plan of China (2012AA062104), the National Natural Science Foundation of China (51375478), the Project funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions (SZBF2011-6-B35) and the Graduate Education Innovation Project of Jiangsu Province (CXLX12_0948).
