Dynamic model of field modulated magnetic gear system

Yuan, Xiaoming; Hao, Xiuhong; Du, Bing; Zhang, Lijie

Journal of Vibroengineering

Browse Journal

Submit article

Published: 15 February 2014

Check for updates

Dynamic model of field modulated magnetic gear system

Xiaoming Yuan¹

Xiuhong Hao²

Bing Du³

Lijie Zhang⁴

^{1, 4}Hebei Provincial Key Laboratory of Heavy Machinery Fluid Power Transmission and Control Yanshan University, Qinhuangdao, 066004, China

²School of Mechanical Engineering, Yanshan University, Qinhuangdao, 066004, China

^{3, 1, 4}Key Laboratory of Advanced Forging & Stamping Technology and Science, Yanshan University Ministry of Education of China, Qinhuangdao, 066004, China

Corresponding Author:

Lijie Zhang

Cite the article Download PDF

Downloads 1165

Abstract

Considering the special working principle and the structure of field modulation magnetic gear (FMMG), the magnetic coupling stiffnesses (MCS) are calculated and analyzed by finite element method. A magnetic coupling dynamic model is presented and the dynamic differential equations are founded. The natural frequencies and mode shapes of FMMG system are investigated. The effects of main design parameters on the natural frequencies are discussed. The results show that MCS are much smaller than the meshing stiffnesses of mechanical gears and are affected greatly by system parameters. Six modes of FMMG system have distinctive features, and six natural frequencies change differently as main parameters increase.

1. Introduction

Magnetic gears can transmit movement and force by the interactive magnetic field between the permanent magnets (PMs). They have some distinct advantages, such as minimum acoustic noise, free from lubrication, inherent overload protection, and so on. Also, they are widely used in the medicine, chemical industry, vehicle, aerospace and other fields. However, the traditional magnetic gears which adopt the parallel shaft topology have a low utilization of PMs and a low torque density. Thus, magnetic gears didn’t get much attention in the 20th century.

Field modulated magnetic gear (FMMG) proposed by K. Atallah adopts the coaxial topology [1, 2]. The utilization of PMs is improved significantly, and FMMG can provide larger torque and higher torque density than the traditional magnetic gears. In some ways, it can become completely comparable with mechanical gears. In the past ten years, FMMG has attracted the attention of many scholars. Static and dynamic characteristics have been extensively carried on, such as transmission mechanism [1, 3], torque characteristics [4], structural optimization [5], transmission efficiency [6, 7], rotor eccentricity [8], and so on. Also, various types of magnetic gears, such as the axial magnetic gear [9], the linear magnetic gear [2], and kinds of the permanent magnet motors [10, 11] are developed. All of these have promoted the rapid application of FMMG in vehicle, marine and other fields [12, 13].

Dynamics of FMMG system are important aspects for comprehensively improving its working performances. Dynamic model and free vibration are basis of in-depth dynamic characteristics of FMMG system. However, due to its non-contact mechanism, the magnetic coupling stiffnesses (MCS) among main components are much smaller than the meshing stiffnesses of mechanical gears, and thus are named weak magnetic coupling stiffnesses (WMCS). FMMG will present many distinct dynamic characteristics, which are totally different from mechanical gears. Although, the long-lasting oscillations caused by WMCS have been discussed by finite element method (FEM) [14], the expressions of WMCS and the dynamic theory model still need to be further confirmed, in order to further explore its dynamic characteristics.

In this paper, based on the magnetic torque of FMMG, WMCS among parts have been given by FEM. A magnetic coupling dynamic model with two subsystems is presented and the dynamic differential equations are founded. The mode characteristics of FMMG system are analyzed fully. The effects of main design parameters on the natural frequencies are discussed. The dynamic model and these results lay the foundation for further dynamic researches and parameters optimization of the magnetic system.

2. Dynamic model and dynamic differential equations of FMMG system

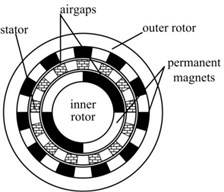
FMMG system shown in Figure 1 consists of four basic elements: (a) the inner rotor; (b) the outer rotor; (c) the stator; (d) PMs arranged on the inner and outer rotors. The stator takes charge of modulating the magnetic fields in two air-gaps beside it.

Fig. 1Topology and prototype of a coaxial magnetic gear

a)

b)

Figure 2 shows the dynamic model of FMMG system with two subsystems, namely, the inner rotor/stator subsystem and the outer rotor/stator subsystem, when the stator is fixed. The magnetic coupling dynamic model employs following assumptions [15]:

(1) Main components of FMMG system are considered to be rigid, assuming that the elastic deformations of main components are negligible.

(2) Magnetic interactions between PMs and the stator are modeled as the linear spring along tangential direction and normal to its axis. Supports of the inner and outer rotors can be equivalent to the transverse linear spring normal to its axis. Constraints between the stator and the foundation are equivalent to the tangential linear spring and the transverse linear spring.

(3) Frictional forces arising from relative motions between components and the foundation are considered to be negligible. Time-varying components of the magnetic coupling stiffnesses due to field modulating are neglected.

(4) Out-of-step doesn’t occur because of the overload. Manufacturing and installation errors of all parts are not included in this paper.

(5) The effects of the inertias connected to FMMG system at the input and output sides are excluded here, considering that these can only cause resonances at very low frequencies.

(6) All PMs on the inner and outer rotors are assumed to be identical with the same size, performance parameters, respectively. Magnetic components and non-magnetic components in the stator have the same sizes and performance parameters, respectively.

Fig. 2Dynamic model of FMMG system

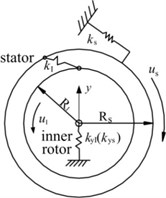
(a) Inner rotor/stator subsystem

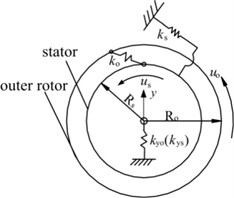
(b) Outer rotor/stator subsystem

The dynamic model of FMMG system allows each parts translate in y directions and rotate about their translation axes. Torsional displacements of the inner rotor, the outer rotor and the stator are $θ_{I}$ , $θ_{o}$ , $θ_{s}$ , respectively. For the sake of convenience, the torsional angular displacements are replaced by their corresponding translational displacements as follows:

u_{i} = R_{i} θ_{i}, i = I, o, s

where $R_{I}$ , $R_{s}$ and $R_{o}$ are the equivalent radius of gyration of the inner rotor, the stator and the outer rotor, respectively.

Transverse vibration displacements of the inner rotor, the outer rotor and the stator are $y_{I}$ , $y_{s}$ , $y_{o}$ , respectively. Then, the generalized displacement vector of FMMG system can be written as:

1

x = {[\begin{matrix} u_{I} & y_{I} & u_{s} & y_{s} & u_{o} & y_{o} \end{matrix}]}^{T} .

2.1. Dynamic differential equations of the inner rotor/stator subsystem

Figure 2(a) shows the dynamic model of the inner rotor/stator subsystem. The undamped equations of the subsystem are given as follows:

2

\{\begin{matrix} \begin{array}{l} M_{I} {\ddot{u}}_{I} + k_{I} x_{I} c o s α = T_{I} / R_{I}, \\ m_{I} {\ddot{y}}_{I} + k_{I} x_{I} s i n α + k_{y I} y_{I} = 0, \\ M_{s} {\ddot{u}}_{s} - k_{I} x_{I} c o s α + k_{s} u_{s} = 0, \end{array} \\ m_{s} {\ddot{y}}_{s} - k_{I} x_{I} s i n α + k_{y s} y_{s} = 0, \end{matrix}

where $m_{I}$ and $m_{s}$ are the masses of the inner rotor and the stator, respectively; $M_{I}$ and $M_{s}$ are the equivalent masses of the inner rotor and the stator along their torsional vibration direction, respectively, $M_{I} = J_{I} / R_{I}^{2}$ , $M_{s} = J_{s} / R_{s}^{2}$ ; $J_{I}$ and $J_{s}$ are the mass moment of inertia of the inner rotor and the stator around their axes, respectively, $J_{I} = m_{I} \cdot R_{I}^{2} / 2$ , $J_{s} = m_{s} \cdot R_{s}^{2} / 2$ ; $k_{I}$ is the magnetic coupling stiffness between the inner rotor and the stator, $k_{I} = \sqrt{k_{I r}^{2} + k_{I t}^{2}}$ , $k_{I r}$ and $k_{I t}$ are the transverse and tangential components of $k_{I}$ , respectively; $k_{y I}$ and $k_{y s}$ are the transverse supporting stiffnesses of the inner rotor and the stator, respectively; $k_{s}$ is the torsional stiffness of the stator around its axis; $x_{I}$ and $α$ are the relative displacement and the meshing angle between the inner rotor and the stator, respectively, $α = a t a n (k_{I r} / k_{I t})$ , $T_{I}$ is the torque on the inner rotor.

The relative displacement $x_{I}$ can be calculated as:

3

x_{I} = (u_{I} - u_{s}) c o s α + (y_{I} - y_{s}) s i n α .

By substituting Eq. (3) into Eq. (2), the undamped dynamic equations of the inner rotor/stator subsystem are given as follows:

4

\{\begin{matrix} \begin{array}{l} M_{I} {\ddot{u}}_{I} + k_{I} (u_{I} - u_{s}) {c o s}^{2} α + k_{I} (y_{I} - y_{s}) s i n α c o s α = T_{I} / R_{I}, \\ m_{I} {\ddot{y}}_{I} + k_{I} (u_{I} - u_{s}) s i n α c o s α + k_{I} (y_{I} - y_{s}) {s i n}^{2} α + k_{y I} y_{I} = 0, \\ M_{s} {\ddot{u}}_{s} - k_{I} (u_{I} - u_{s}) {c o s}^{2} α - k_{I} (y_{I} - y_{s}) s i n α c o s α + k_{s} u_{s} = 0, \\ m_{s} {\ddot{y}}_{s} - k_{I} (u_{I} - u_{s}) s i n α c o s α - k_{I} (y_{I} - y_{s}) {s i n}^{2} α + k_{y s} y_{s} = 0 . \end{array} \end{matrix}

2.2. Dynamic differential equations of the outer rotor/stator subsystem

Figure 2(b) shows the dynamic model of the outer rotor/stator subsystem. The undamped equations of the subsystem can be expressed as follows:

5

\{\begin{matrix} \begin{array}{l} M_{o} {\ddot{u}}_{o} + k_{o} x_{o} c o s β = T_{o} / R_{o}, \\ m_{o} {\ddot{y}}_{o} + k_{o} x_{o} s i n β + k_{y o} y_{o} = 0, \\ M_{s} {\ddot{u}}_{s} - k_{o} x_{o} c o s β + k_{s} u_{s} = 0, \\ m_{s} {\ddot{y}}_{s} - k_{o} x_{o} s i n β + k_{y s} y_{s} = 0, \end{array} \end{matrix}

where $m_{o}$ , $M_{o}$ , $J_{o}$ are the mass, the equivalent mass, the mass moment of inertia of the outer rotor, respectively, $M_{o} = J_{o} / R_{o}^{2}$ , $J_{o} = m_{o} \cdot R_{o}^{2} / 2$ ; $k_{o}$ is the magnetic coupling stiffness between the outer rotor and the stator, $k_{o} = \sqrt{k_{o r}^{2} + k_{o t}^{2}}$ ; $k_{o r}$ and $k_{o t}$ are the transverse and tangential components of $k_{o}$ , respectively; $k_{y o}$ is the transverse supporting stiffness of the outer rotor; $T_{o}$ is the torque on the outer rotor; $x_{o}$ and $β$ are the relative displacement and the meshing angle between the outer rotor and the stator, respectively, $β = atan (k_{o r} / k_{o t})$ .

The relative displacement $x_{o}$ can be given as:

6

x_{o} = (u_{s} - u_{o}) c o s β + (y_{s} - y_{o}) s i n β .

By substituting Eq. (6) into Eq. (5), the dynamic differential equations of the outer rotor/stator subsystem are:

7

\{\begin{matrix} \begin{array}{l} M_{o} {\ddot{u}}_{o} + k_{o} (u_{s} - u_{o}) {c o s}^{2} β + k_{o} (y_{s} - y_{o}) s i n β c o s β = T_{o} / R_{o}, \\ m_{o} {\ddot{y}}_{o} + k_{o} (u_{s} - u_{o}) s i n β c o s β + k_{o} (y_{s} - y_{o}) {s i n}^{2} β + k_{y o} y_{o} = 0, \\ M_{s} {\ddot{u}}_{s} - k_{o} (u_{s} - u_{o}) {c o s}^{2} β - k_{o} (y_{s} - y_{o}) s i n β c o s β + k_{s} u_{s} = 0, \\ m_{s} {\ddot{y}}_{s} - k_{o} (u_{s} - u_{o}) s i n β c o s β - k_{o} (y_{s} - y_{o}) {s i n}^{2} β + k_{y s} y_{s} = 0 . \end{array} \end{matrix}

3. The overall system

The dynamic differential equations of the overall FMMG system can be obtained by the combination of equations (4) and (7) which define the dynamic differential equations of individual subsystem. The undamped differential equations of FMMG system are given in matrix form as:

8

m \ddot{x} + k x = F .

The mass matrix $m$ , the stiffness matrix $k$ and the load vector $F$ are given respectively as follows:

m = diag ([\begin{matrix} M_{I} & m_{I} & M_{f} & m_{f} & M_{o} & m_{o} \end{matrix}]),

\begin{array}{l} K = [\begin{matrix} k_{I} {c o s}^{2} α & k_{I} s i n α c o s α & - k_{I} {c o s}^{2} α \\ k_{I} s i n α c o s α & k_{I} {s i n}^{2} α + k_{y I} & - k_{I} s i n α c o s α \\ - k_{I} {c o s}^{2} α & - k_{I} s i n α c o s α & k_{I} {c o s}^{2} α + k_{o} {c o s}^{2} β + k_{s} \\ - k_{I} s i n α c o s α & - k_{I} {s i n}^{2} α & k_{I} s i n α c o s α + k_{o} s i n β c o s β \\ 0 & 0 & - k_{o} {c o s}^{2} β \\ 0 & 0 & - k_{o} s i n β c o s β \end{matrix} \\ \begin{matrix} - k_{I} s i n α c o s α & 0 & 0 \\ - k_{I} {s i n}^{2} α & 0 & 0 \\ k_{I} s i n α c o s α + k_{o} s i n β c o s β & - k_{o} {c o s}^{2} β & - k_{o} s i n β c o s β \\ k_{I} {s i n}^{2} α + k_{o} {s i n}^{2} β + k_{y s} & - k_{o} s i n β c o s β & - k_{o} {s i n}^{2} β \\ - k_{o} s i n β c o s β & k_{o} {c o s}^{2} β & k_{o} s i n β c o s β \\ - k_{o} {s i n}^{2} β & k_{o} s i n β c o s β & k_{o} {s i n}^{2} β + k_{y o} \end{matrix}], \end{array}

F = {[\begin{matrix} - T_{I} / R_{I} & 0 & 0 & 0 & - T_{o} / R_{o} & 0 \end{matrix}]}^{T}

Free vibration differential equations of FMMG system are written in matrix form as:

9

m \ddot{x} + k x = 0 .

4. The magnetic coupling stiffness

The static torques of the example FMMG system shown in Table 1 can be computed at each angular position by means of 2D FEM analysis shown in Fig. 3, integrating the Maxwell stress tensor. The experiments of the static torque can be carried out on the prototype of FMMG system. The inner rotor was jointed with the motor shaft, and the outer rotor was fastened to the shaft of the magnetic powder loader. The torque sensors were fixed on the shafts of the inner and outer rotors. When the outer rotor was not running and the inner rotor was drived slowly, the static torque characteristics of FMMG system were measured.

Fig. 3The FEM model of FMMG system

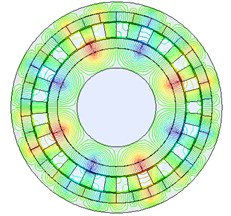
(a) Calculated flux lines

(b) Arrangements of PMs segments

The tangential and transverse magnetic forces on the rotors can be calculated by FEM. The tangential and transverse components of the magnetic coupling stiffnesses can be obtained by:

10

k_{i r} = d F_{i r} / d r,

11

k_{i t} = d F_{i t} / d u_{i t} = d F_{i t} / (R_{i} d θ),

where $F_{i r}$ and $F_{i t}$ are the transverse and tangential magnetic forces, respectively, with $i = I, o$ ; $k_{i r}$ and $k_{i t}$ are the transverse and tangential magnetic coupling stiffnesses, respectively; $r$ is the radius of a point on the PMs to the axis; $θ$ is the position angle between the $x$ axis and the center line of each PM segment when the inner and outer rotors are a relative position.

Table 1Parameters of the example FMMG system

Number of pole pairs on the inner rotor	4	Number of pole pairs on the inner rotor	17
Number of the ferromagnetic pole pieces	21	Outer radius of the outer rotor yoke / mm	214
Inside radius of the outer rotor yoke / mm	194	Thickness of PMs on the outer rotor / mm	10
Outer radius of the outer airgap / mm	174	Inside radius of the outer airgap / mm	172
Outer radius of the inner airgap / mm	142	Inside radius of the inner airgap / mm	140
Outer radius of the inner rotor yoke / mm	120	Inside radius of the inner rotor yoke / mm	80
Thickness of PMs on the inner rotor / mm	10	Axial length / mm	40
Remanence of PMs / T	1.3	Coercive force of PMs / KOe	11.6

Fig. 4 indicates that the static torques vary sinusoidally with the relative mechanical angles between the inner and outer rotors. When the number of pole pairs on the inner rotor is $p_{1}$ , the period of the static torques is $2 π / p_{1}$ . Torque ratio of the inner and outer rotors is always equal to the transmission ratio of FMMG system, that is, 4.25. Although there are little errors between FEM and the experiment, the results of FEM have high consistency with the results calculated by Du [7] and can meet the computing requirements.

Fig. 4Torque-angle curves of FMMG system

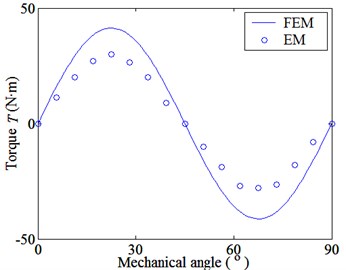
(a) Inner rotor

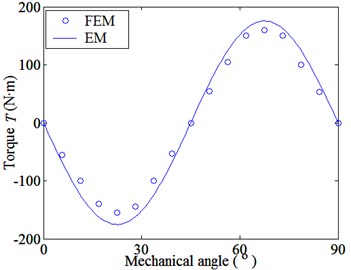
(b) Outer rotor

Fig. 5 indicates that the tangential magnetic forces and the tangential magnetic coupling stiffnesses among parts vary sinusoidally with the relative mechanical angle too. When there isn’t relative rotation between the inner and outer rotors, FMMG system will stabilize at zero point, also called no-load point or the balance point, that is, there aren’t output torque on the outer rotor. At this point, the tangential magnetic forces and the magnetic tangential coupling stiffnesses are zero. As the relative rotation angle increases and comes to the angle, which is corresponding to half of the arc length of PMs on the inner rotor, the torque, the tangential magnetic forces and the tangential magnetic coupling stiffnesses all achieve the maxima.

Fig. 5Magnetic forces and magnetic coupling stiffnesses among parts

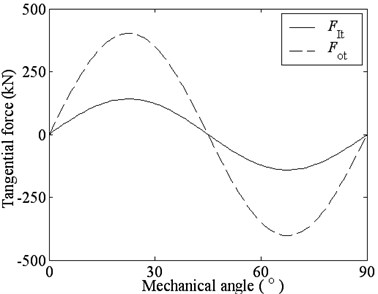
(a) Tangential magnetic force

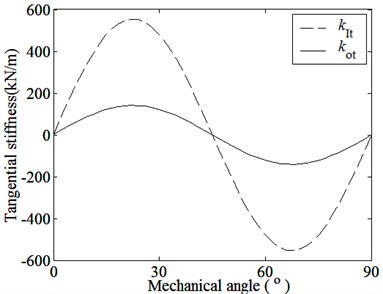
(b) Tangential magnetic coupling stiffness

(c) Transverse magnetic force

(d) Transverse magnetic coupling stiffness

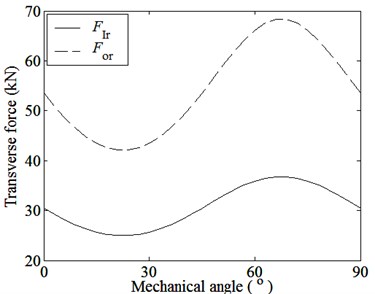
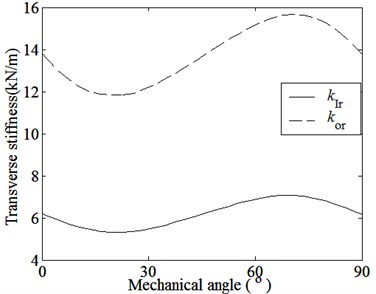
The transverse magnetic forces and the transverse magnetic coupling stiffnesses among parts vary periodically with the mechanical angle increasing, and the average values are not zero. When the relative rotation angle becomes to half of the arc length of PMs on the inner rotor, the transverse magnetic forces and the transverse magnetic coupling stiffnesses will reach the minimum.

Fig. 5 indicates that the transverse magnetic coupling stiffnesses are much smaller than the tangential magnetic coupling stiffnesses. That is because the transverse magnetic forces on the inner and outer rotors is a uniform distribution along the entire circumference, the sum of the transverse magnetic forces and the corresponding transverse magnetic coupling stiffnesses are less.

5. Free vibration of FMMG system

The weak magnetic coupling stiffnesses of FMMG system decrease with the output torque decreasing. Table 2 shows the parameters of FMMG system with a full load and Table 3 shows the mode frequencies and mode shapes.

Table 2Characteristic parameters of the example system

$k_{I}$ (KN/m)	$k_{o}$ (KN/m)	$k_{f}$ (MN/m)	$k_{y I}$ (MN/m)	$k_{y o}$ (MN/m)	$k_{y s}$ (MN/m)	$m_{I}$ (kg)	$m_{s}$ (kg)	$m_{o}$ (kg)
141.2	554.2	1	1	1	1	3.5	2.5	5.6

Table 3Mode frequencies and mode shapes of magnetic gearing system

	IR rotational mode	IR translational mode	S rotational mode	S translational mode	OR rotational mode	OR translational mode
Natural frequencies (rad/s)	256.7	534.6	1197.4	637.4	366.7	422.8
Mode shapes	1.0000 –0.0075 0.1801 0.0085 0.2706 –0.0023	0.0182 1.0000 0.0037 0.0009 –0.0084 –0.0003	–0.0595 –0.0019 1.0000 0.0100 –0.1601 –0.0026	0.0068 0.0006 0.0227 –1.0000 0.0055 0.0001	0.4741 –0.0106 –0.3185 –0.0075 –1.0000 0.0435	–0.0291 0.0012 0.0355 0.0010 0.0733 1.0000

Table 3 shows that there are six modes, whose shapes and natural frequencies are completely different. In mode shapes corresponding to natural frequencies 256.7 rad/s, 1197.4 rad/s and 366.7 rad/s, the relative deflections of the torsional degree of freedom (DOF) are much bigger than the relative deflections of transverse DOF. In mode shapes corresponding to natural frequencies 534.6 rad/s, 637.4 rad/s and 422.8 rad/s, all relative deflections are little except a certain transverse DOF. Considering the shape characteristics, the shapes corresponding to 256.7 rad/s, 1197.4 rad/s and 366.7 rad/s are named the rotational modes of the inner rotor, the stator and the outer rotor (IR, S and OR rotational modes), respectively. Other three shapes are named the transverse modes of the inner rotor, the stator and the outer rotor (IR, S and OR transverse modes), respectively.

The natural frequencies of FMMG prototype are tested by the impact method. Due to the structure, vibrations of the inner rotor can’t be detected. But from the rotational and transverse vibrations of the outer rotor and the stator, six natural frequencies can be confirmed, that is 232 rad/s, 335 rad/s, 451 rad/s, 561 rad/s, 644 rad/s and 1248 rad/s. Because of the manufacturing deviations of FMMG prototype and detection deviations, there are certain errors between the experimental results and theoretical results. But natural frequencies of the experimental results are roughly corresponding to theoretical results. These demonstrate that the magnetic coupling dynamic model is feasible.

6. Changes of natural frequencies along with main design parameters

Fig. 6 shows the changes of natural frequencies along with main design parameters. We know:

(1) Natural frequencies of all modes increase with the output torque and the remanence of PMs increasing. Natural frequencies of all rotational modes significantly increase and other frequencies have little changes. These are because that the magnetic coupling stiffnesses $k_{I}$ and $k_{o}$ shown in Fig. 5 and Fig. 7(a) increase as the output torque and the remanence of PMs increase.

Fig. 6Changes of natural frequencies along with the main parameters

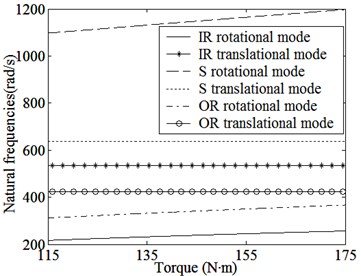
(a) Changes of natural frequencies along with $T$

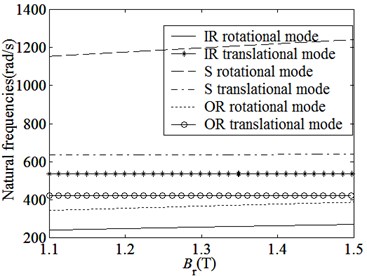
(b) Changes of natural frequencies along with $B_{r}$

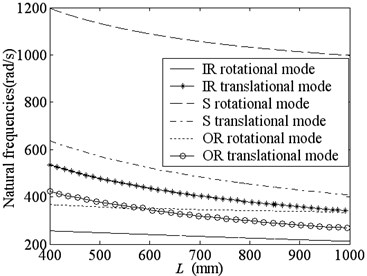
(c) Changes of natural frequencies along with $L$

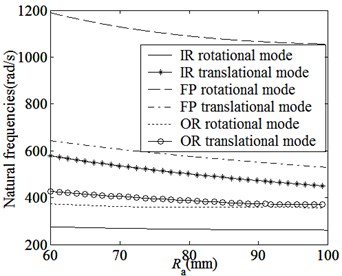
(d) Changes of natural frequencies along with $R_{a}$

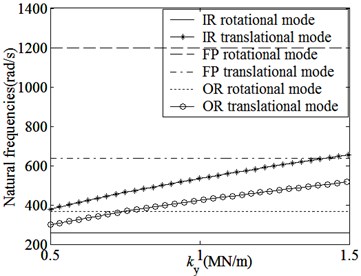
(e) Changes of natural frequencies along with $k_{y I}$ and $k_{y s}$

(2) Natural frequencies of all modes decrease with the axial length $L$ increasing. But natural frequencies of IR and OR rotational modes decrease slowly and other frequencies decrease quickly. These can be explained that the magnetic coupling stiffnesses $k_{I}$ and $k_{o}$ shown in Fig. 7(b), the mass of all parts proportionally increase, but other stiffnesses change little when the axial length $L$ increases.

(3) When the thickness of the airgaps, PMs and the yokes of the inner and outer rotors are constants, natural frequencies of IR and OR rotational modes slightly decrease and other frequencies obviously decrease as the outer radius of the inner rotor yoke $R_{a}$ increase. Because the magnetic coupling areas between the inner and outer rotors increase rapidly with $R_{a}$ increasing, the magnetic coupling stiffnesses shown in Fig. 7(c) and the masses of all parts increase, but other stiffnesses change little.

(4) The supports have great influences on the transverse supporting stiffnesses of main parts. Natural frequencies of IR and OR transverse modes decrease rapidly as the transverse supporting stiffnesses $k_{y I}$ and $k_{y s}$ decrease, but other natural frequencies change little.

Different from the mesh stiffnesses of mechanical gears, which are hardly affected by tooth width and output torque, the weak magnetic coupling stiffnesses of FMMG system increase with the increase of the axial length and the output torque, when the system runs with no overload.

All main parameters affect the natural frequencies of FMMG system, and the influences of the remanence of PMs and the axial length are especially greater. Considering the exciting sources in working conditions, the dynamics, such as resonances, can be avoided by parameter optimization and provide references for improving dynamic performances of FMMG system.

Fig. 7Curves of magnetic coupling stiffnesses curves with main parameters

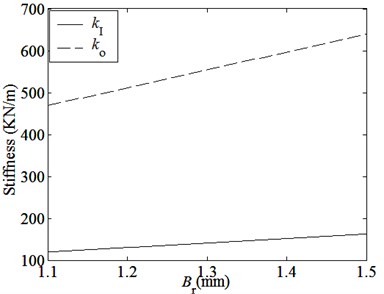
(a) Magnetic coupling stiffnesses curves with $B_{r}$

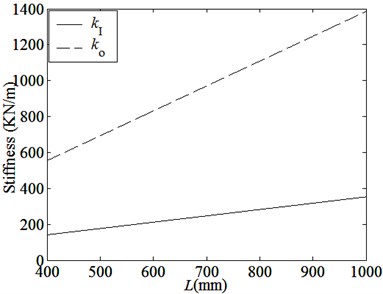
(b) Magnetic coupling stiffnesses curves with $L$

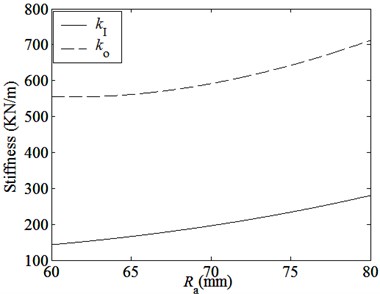
(c) Magnetic coupling stiffnesses curves with $R_{a}$

7. Conclusions

In this paper, the weak magnetic coupling stiffnesses of FMMG system have been calculated by FEM, which are much smaller than the mesh stiffnesses of mechanical gears and are affected by the design parameters, such as the remanence of PMs. Besides, the magnetic coupling dynamic model of FMMG system and the dynamic differential equations have been founded. The mode characteristics of three rotational modes and three transverse modes are also summarized. The effects of main parameters on the natural frequencies as well as the corresponding to the reasons have been discussed. These research results will provide reference for the design and manufacture of FMMG system.

References

K. Atallah, D. Howe A novel high-performance magnetic gear. IEEE Transactions on Magnetics, Vol. 37, Issue 4, 2001, p. 2844-2846.

Search CrossRef
K. Atallah, J. Wang, D. Howe A high-performance linear magnetic gear. Journal of Applied Physics, Vol. 97, Issue 10, 2005, p. N516-N516-3.

Search CrossRef
P. O. Rasmussen, T. O. Andersen, F. T. Joergense, O. Nielsen Development of a high performance magnetic gear. IEEE Transactions on Industry Applications, Vol. 41, Issue 3, 2005, p. 764-770.

Search CrossRef
N. Niguchi, K. Hirata, Y. Hayakawa Study on transmission torque characteristics of a surface-permanent- magnet- type magnetic gear. IEEJ Transactions on Industry Applications, Vol. 131, Issue 3, 2011, p. 396-402-23.

Search CrossRef
L. N. Jian, G. Xu, J. Song, H. Xue, et al. Optimum design for improving modulating- effect of coaxial magnetic gear using response surface methodology and genetic algorithm. Progress in Electromagnetics Research, Vol. 116, 2011, p. 297-312.

Search CrossRef
Linni Jian, K. T. Chau A coaxial magnetic gear with halbach permanent-magnet arrays. IEEE Transactions on Energy Conversion, Vol. 25, Issue 2, 2003, p. 319-328.

Search CrossRef
Du Shiqin, Jiang Jianzhong, Zhang Yuejin, Gong Yu A magnetic gearing. Transactions of China Electrotechnical Society, Vol. 25, Issue 9, 2010, p. 41-46.

Search CrossRef
L. A. Percebon, R. Ferraz, D. L. Ferreira, V. Mauricio Modelling of a magnetic gear considering rotor eccentricity. IEEE International Electric Machines and Drives Conference, 2011, p. 1237-1241.

Search CrossRef
S. Mezani, K. Atallah, D. Howe A high-performance axial-field magnetic gear. Journal of Applied Physics, Vol. 99, Issue 8, 2006, p. 08R303.

Search CrossRef
Linni Jian, K. T. Chau, J. Z. Jiang A magnetic-geared outer-rotor permanent-magnet brushless machine for wind power generation. IEEE Transactions on Industry Applications, Vol. 45, Issue 3, 2009, p. 954-962.

Search CrossRef
P. O. Rasmussen, H. H. Mortensen, T. N. Matzen, et al. Motor integrated permanent magnet gear with a wide torque-speed range. IEEE Energy Conversion Congress and Exposition, 2009, p. 1510-1518.

Search CrossRef
Xiaoyong Zhu, Long Chen, Li Quan, et al. A new magnetic-planetary-geared permanent magnet brushless machine for hybrid electric vehicle. IEEE Transactions on Magnetics, Vol. 48, Issue 11, 2012, p. 4642-4645.

Search CrossRef
N. W. Frank, H. A. Toliyat Gearing ratios of a magnetic gear for marine applications. IEEE Electric Ship Technologies Symposium, Maryland, USA, 2012, p. 477-481.

Search CrossRef
N. W. Frank, S. Pakdelian, H. A. Toliyat Passive suppression of transient oscillations in the concentric planetary magnetic gear. IEEE Transactions on Energy Conversion, Vol. 26, Issue 3, 2011, p. 933-939.

Search CrossRef
Ahmet Kahraman Free torsional vibration characteristics of compound planetary gear sets. Mechanism and Machine Theory, 2011, p. 953-971.

Search CrossRef

About this article

Received

17 October 2013

Accepted

07 November 2013

Published

15 February 2014

Keywords

field modulated

magnetic gear

dynamic model

free vibration

Acknowledgements

This project is supported by Natural Science Foundation of China (51205341, 51275438), Research Program of Natural Science at Universities of Hebei Province (Q2012032), the Joint Fund of Specialized Research Fund for the Doctoral Program of Higher Education and Hebei Provincial Education Office (20121333120004).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.