The aeroelastic analysis of two different wind turbine blades

1. Introduction

Wind electricity has become one of the most important representatives as the new energy and clean energy in the world. Wind turbines are focusing on the upsizing with the developing of the wind electricity industry. As one of the most critical parts of the wind turbine, the wind turbine blade is moving for the direction of more upsizing and flexibilily [1]. Because the flutter wind turbine blade will give rise to the severe accident, the aeroelatic problem of the wind turbine, especially the dynamic aeroelaticity, that is, flutter, has been one of the key subjects of relative fields [2, 3]. Zhang J. P. et al. researched the dynamic stability of large wind turbine blade under complicated offshore wind conditions [4]. Many researchers have made the studies of wind turbine flutter, totally in two aspects, frequency domain analysis and the time domain analysis. So they could get the critical flutter speed using the frequency domain analysis [5, 6], M. H. Hansen solved the flutter of the wind turbine blade with eigenvalue approach [7].

P. K. Chaviaropoulos presented a numerical tool for investigating the aeroelastic stability, that is, the stall flutter, of a single wind turbine blade subjected to combined flp/lead-lag motion, based on the extended ONERA lift and drag models [8, 9]. S. Sarkar investigated the nonlinear aeroelastic behavior of a two-dimensional rotor blade in the dynamic stall regime [10].

However, there are little researches for the flutter of wind turbine blade airfoil using the time domain analysis method combined with the eigenvalue method. These two methods will be used to determine the flutter region of the wind turbine blade airfoil respectively.

The outlines of the paper are: the structural model of wind turbine blade airfoil, the eigenvalue approach for the flutter of wind turbine blade airfoil, the time domain solution to the aeroelastic response of the blade airfoil, the numerical simulation and results analysis and the conclusions in the end.

2. The structural model of wind turbine blade airfoil

Fig. 1 shows the two-dimension model of wind turbine blade, that is, the airfoil of wind turbine blade. The aerodynamic force $F$ and aerodynamic torque $M$ under the air fluid will apply on the blade of wind turbine. The aerodynamic force can be divided into lift $L$ and drag $D$, which is vertical and parallel to the velocity of air fluid respectively.

Fig. 1The airfoil of wind turbine blade

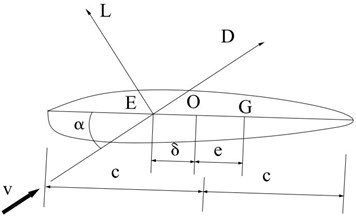
Where $E$ is the aerodynamic center, $G$ means the center of mass of airfoil, $O$ is the center of stiffness, $e$ denotes the distance between the center of mass and center of stiffness, $\alpha$ is angle of attack, $\delta$ means the distance between the aerodynamic center and the center of stiffness.

The differential equation of motion for the airfoil will be seen as Eq. (1):

where $J_0$ is the moment of inertia of the airfoil around the center of mass, $m$ is the mass of airfoil, $s$ is the stiffness of linear spring, $k$ is the stiffness of torsion spring.

The aerodynamic force $F$ and torque $M$ are very complicated and nonlinear, there are some ways to calculate them. According to [11], the aerodynamic force and torque can be given as Eq. (2) based on the aerodynamic stiffness and aerodynamic damping:

where $S_{11},S_{12},S_{21},S_{22}$ mean the aerodynamic stiffness, $d_{11},d_{12},d_{21},d_{22}$ denote the aerodynamic damping.

3. The eigenvalue approach for the flutter of wind turbine blade airfoil

In order to calculate the aerodynamic force and aerodynamic torque and to solve the Eq. (1), assume that there is no relations between the flap displacement, the rotate angle and the aerodynamic loads. That is to say, $S_{12}=S_{22}=\text{0}$, $d_{11}=d_{21}\text{=}\text{0}$. So the other aerodynamic stiffness and aerodynamic damping can be expressed as Eq. (3) [11]:

where $\rho$ is the density of air, $c$ is the semi-chord length, $B$ is the number of blades of wind turbine, $C_L$ means the lift coefficient, $C_D$ means the drag coefficient. $W_0\text{=}\sqrt{{\text{(}R\mathrm{\Omega }\text{)}}^2\text{+}{V}_0^2}$ means relative velocity, $V_0$ is the velocity of air fluid, is the radius of blade, $\mathrm{\Omega }$ is the rotating angular velocity. $\lambda$ is the tip speed ratio.

Substituting the Eq. (3) into Eq. (1), the following equation will be obtained as Eq. (4):

The eigenvalue equation of the Eq. (4) is as:

So the Eq. (5) will be changed into Eq. (6):

where $r_0=s(e{S}_{21}+k+S_{11})$, $r_1=d_{22}\left(k+e^{2}s+S_{11}\right)-d_{12}\left(S_{21}-es\right)$,

$r_2=s{J}_0+m(k+e^{2}s+S_{11})$, $r_3=J_0{d}_{22}$, $r_4\text{=}m{J}_0$.

The eigenvalue will be solved as Eq. (7):

Therefore, the stability of the airfoil aeroelasticity will be judged directly according to sign of the real part of the eigenvalues of the wind turbine blade. If the real part is positive, it means the wind turbine blade is unstable and the flutter will occur, and if the real part is minus, it means the wind turbine blade in stable and the flutter will not occur. Under the same tip speed ratio, if only there is one unstable real part of eigenvalue, the wind turbine blade will be considered unstable, that is, the flutter will occur, at the given tip speed ratio. According to the rules of flutter determination, the flutter region of the wind turbine blade will be given directly by the eigenvalue approach.

4. The time domain solution to the aeroelastic response of blade airfoil

Considering Eq. (1), the four-order Runge-Kutta method was used to calculate the aeroelastic responses of wind turbine blade. Firstly, let:

Then the first-order equation and the other order equation were seen as Eq. (9) and Eq. (10):

where $k_1$, $l_1$, $p_1$, $q_1$, $k_2$, $l_2$, $p_2$, $q_2$, $k_3$, $l_3$, $p_3$, $q_3$, $k_4$, $l_4$, $p_4$, $q_4$ are the parameters for the Runge-Kutta method, which can be determined by Eq. (9).

The solution procedure in time domain can be expressed as:

1) Initialize ${\theta }_0$, $\mathrm{}{\dot{x}}_0$.

2) Calculate the initial aerodynamic force and torque from Eq. (2).

3) Solve the new values of ${\theta }_1$, ${\dot{\theta }}_1$, $\dot{x}$, $x$ at the next step using the Runge-Kutta method.

4) Solve the new aerodynamic force and aerodynamic torque from Eq. (2).

5) Repeat the 3), 4) and 5) procedures until the end condition was met.

6) At last, the flap displacement and torsion angular displacement, the flap velocity and torsional angular velocity will be obtained.

5. The numerical simulation and results analysis

In order to discuss the results of the time domain analysis of wind turbine blade together with the eigenvalue approach, two different airfoils, that is, NACA63-418 and FX77-W-153, are applied. The structural parameters and the section parameters of airfoil NACA63-418 are as: elastic modulus is 22 GPa, shear modulus is 8.27 GPa, air density is 1.225 kg/m³, axial moment of inertia is 22174 cm⁴, mean radius is 17 m, mass is 8.39 kg, chord is 0.9775 m, section area is 106.88.1 cm², polar moment of inertia is 2165200 cm⁴, torsional center in chordwise is 0.35 chord, angle of incidence is 1.26 deg, moment of inertia is 1.6997 kgm².

The structural parameters and the section parameters of airfoil FX77-W-153 are as: elastic modulus is 22 GPa, shear modulus is 8.27 GPa, air density is 1.225 kg/m³, axial moment of inertia is 17453 cm⁴, mean radius is 10 m, mass is 185 kg, chord is 1.073 m, section area is 1093.1 cm², polar moment of inertia is 676010 cm⁴, torsional center in chordwise is 0.35 chord, angle of incidence is 1.63 deg, moment of inertia is 11.492 kgm².

According to the eigenvalue approach mentioned above, the real parts of eigenvalues under different tip speed ratios for the two different airfoils will be curved as Fig. 2 and Fig. 3.

Fig. 2The real part of unstable eigenvalues for airfoil NACA63-418

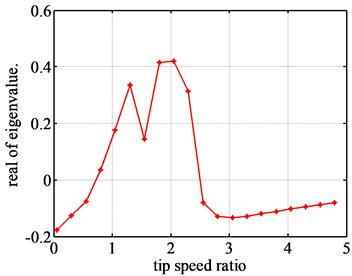
Fig. 3The real part of unstable eigenvalues for airfoil FX77-W-153

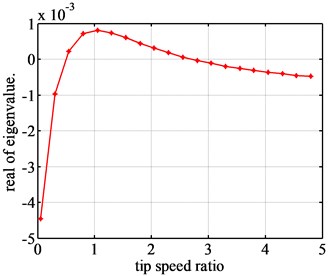
For each airfoil, there are four eigenvalues in all, and there are two real parts curves of stable eigenvalues and two real parts curves of two unstable eigenvalues. Fig. 2 is the real part curve of one of unstable eigenvalues for Airfoil NACA63-418. Fig. 3 is the real part curve of one of unstable eigenvalues for airfoil FX77-W-153.

Fig. 2 shows that the airfoil NACA63-418 will be unstable, for the real parts of the eigenvalues are positive during [0.73, 2.48]. That is to say, the flutter of blade airfoil will occur during [0.73, 2.48]. Therefore, [0.73, 2.48] can be considered as the flutter region of NACA63-418 airfoil. As for the airfoil FX77-W-153, the flutter region will be [0.5, 2.5]. In addition, the values of the unstable real part of airfoil NACA63-418 are much bigger than those of the airfoil FX77-W-153. And the unstable real part of airfoil NACA63-418 changes very dramatically, while the unstable real part of airfoil FX77-W-153 changes quite slightly. So, it can be found that the flutter of airfoil FX77-W-153 will be slightly, and the flutter of the airfoil NACA63-418 will be dramatically. But the much more detail information about the flutter can’t be found using the eigenvalue approach.

Then the time domain analysis of two wind turbine blade airfoils is also carried out by the four-order Runge-Kutta method, using the different tip speed ratios. There are four different responses, such as: the torsional angular displacement and velocity, flap displacement and the flap velocity of the two different wind turbine blade airfoils. The torsional motion keeps almost stable when the tip speed ratio changes. The flap motion shows very complicated phenomenon than the torsional one. And the flap displacement and the velocity change in very similar way with just the difference in dimension. So in the following part of the paper, the flap displacement will be chosen to analyze the flutter of the wind turbine blade airfoil.

There is extremely complicated changing tread for the flap displacement, so the flutter of the wind turbine blade airfoil will change extremely complicated.

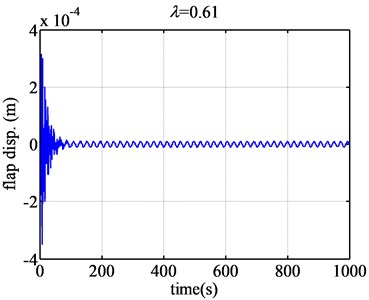
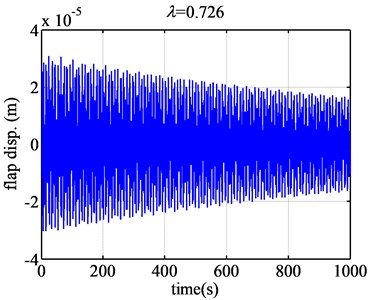
Fig. 4The flap displacement responses of airfoil NACA63-418 when λ are 0.61 and 0.726

a)

b)

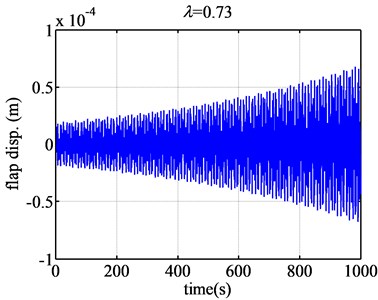
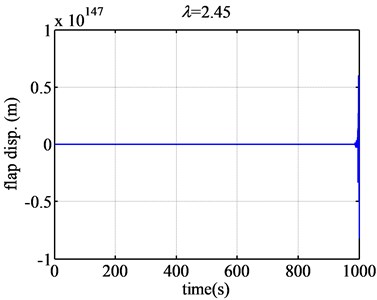
Fig. 5The flap displacement responses of airfoil NACA63-418 when λ are 0.73 and 2.45

a)

b)

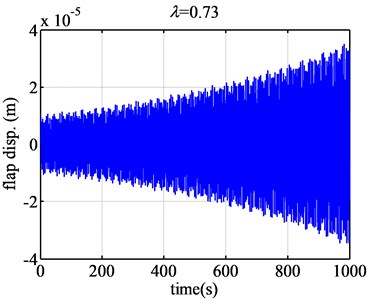
According to Fig. 4, when the tip speed ratio is 0.61, the flap displacement of the blade airfoil NACA63-418 converges greatly. When tip speed ratio is 0.726, the flap displacement of the blade airfoil converges slightly. However, according to Fig. 5, when the tip speed ratio becomes 0.73, the flap displacement of the blade NACA63-418 airfoil diverges slightly. When the tip speed ratio changes a little, just from 0.726 to 0.73, the aeroelastic response changes from convergence to divergence. So the flutter of wind turbine blade will occur of great sudden, but the flutter magnitude is just relative small.

Then the tip speed ratio increases from 0.73 on, the divergence becomes more and more dramatically. When the tip speed ratio becomes larger and larger, the divergence becomes more and more dramatically according to the value of longitudinal coordinates. What is more, based on Fig. 5, when the tip speed ratio is about 2.45, the flap displacement response will diverge the most seriously, the flutter will occur extremely dramatically. So 2.45 is the dangerous tip speed ratio, should be avoided in the design of the wind turbine blade.

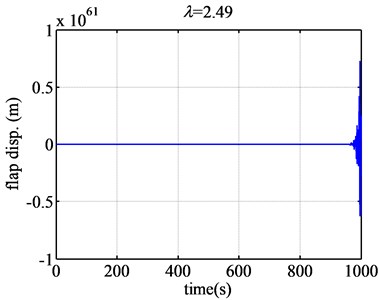
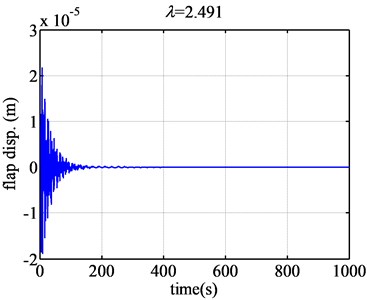
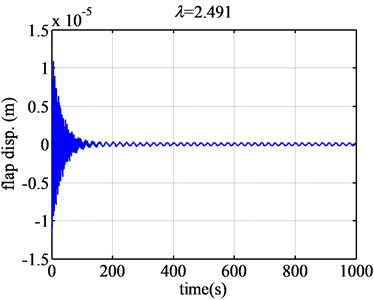
When the tip speed ratio increases much larger, such as 2.49 (Fig. 6), the flap displacement response will diverge less dramatically than that of 2.45. When the tip speed ratio increases to 2.491 (Fig. 6), the flap displacement will converge. So the aeroelastic response will change from divergence to convergence, the flutter will not occur when the tip speed ratio is bigger than 2.491. It can be seen that the flap displacement will change from divergence to convergence suddenly.

Fig. 6The flap displacement responses of airfoil NACA63-418 when λ are 2.49 and 2.491

a)

b)

Therefore, based on the time domain analysis of the flutter of NACA63-418 airfoil, the flutter region will be [0.726, 2.491]. 0.726 and 2.491 can be treated as the lower critical tip speed ratio and the higher tip speed ratio. The flutter region [0.73, 2.48] provided by the eigenvalue approach accurately coincides with the flutter region given by the time domain analysis method.

In order to check whether the unstable flutter is caused by the wind turbine blade aeroelatic model itself or accumulating numerical error, the original integration step was divided by half, and the numerical simulation was carried out again, using the time domain analysis method.

The flutter region provided by the new half step is same with the former one, that is to say, is also [0.726, 2.491]. The flutter region doesn’t change at all. And the time domain response given by half step changes only by the magnitude of vertical coordinates. As two examples, Fig. 7 gives the time domain response of the flap displacement when the tip speed ratios are 0.73 and 2.491 respectively. Compared with Fig. 5 and Fig. 6, there are not any differences in addition to the magnitude of the vertical coordinates and the density of the response curve. Therefore, the results simulated with two different integration steps proven that the unstable flutter in responses is just caused by the aeroelastic model wind turbine blade, not by other reasons, such as the accumulating numerical error.

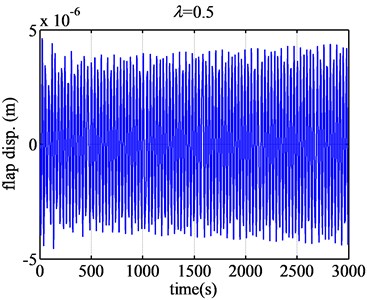
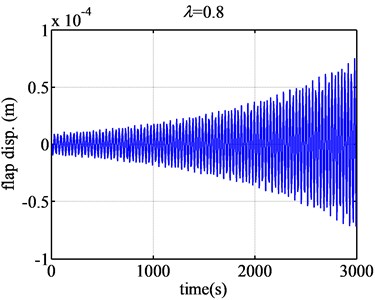
Fig. 8 gives the flap displacement responses of FX77-W-153 when the tip speed ratios are 0.5 and 0.8. When the tip speed ratio is below 0.5, the flap displacement converges. But when the tip speed ration becomes 0.5, the aeroelastic responses will be found between the divergence and convergence, so 0.5 is critical for the blade flutter. And around the tip speed ratio, the divergence and convergence changes smoothly not suddenly. It doesn’t look like that of the airfoil NACA63-418.

Fig. 7The flap displacement responses of airfoil NACA63-418 when λ are 0.73 and 2.491 with half step

a)

b)

Fig. 8The flap displacement responses of airfoil FX77-W-153 when λ are 0.5 and 0.8

a)

b)

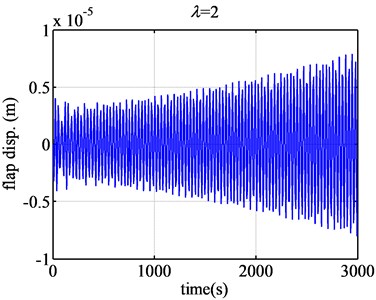
When the tip speed ratio continually grows larger, 0.8 e.g. the flap displacement response will become a little dramatically divergent. However, when the tip speed ratio becomes much larger, such as 2 (Fig. 9), the flap displacement begins to diverge but not so dramatically. However, the flutter extents are very small than that the form airfoil.

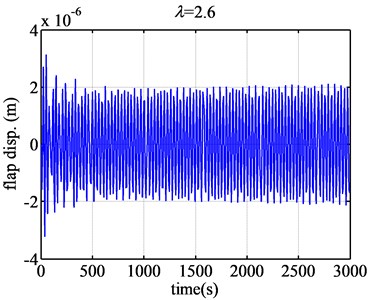
When the tip speed ratio becomes 2.6 (Fig. 9), the aeroelatic responses will become convergent from divergence. So 2.6 is critical condition. Under the condition, the flap displacement and flap velocity converge. From 2.6 on, when the tip speed ratio grows large, the aeroelstic responses will converge. The flutter region of FX77-W-153 airfoil will be obtained as [0.5, 2.6]. 0.5 is the low critical tip speed ratio, and 2.6 is the high critical tip speed ratio.

Based on the eigenvalue solution and the time domain analysis of two different airfoils, NACA63-418 and FX77-W-153, there are many results can be acquired.

The eigenvalue approach gives the flutter region of wind turbine blade directly by the sign of the real part of the eigenvalues of the wind turbine blade. The overall flutter extents can also be judged according to the values of the real part of the eigenvalues. But the flutter detail information and the dangerous tip speed ratio can’t be gotten. While the time domain analysis method can provide the detail information of any tip speed ratio as required and the detail process from stability to flutter and from flutter to stability. And there are two critical tip speed ratios, one is the lower tip speed ratio and another is the higher tip speed ratio. For the two kinds of airfoil, the flutter regions given by these two methods can coincide with each other. In addition, there are some differences between the aeroelasticities of the airfoil NACA63-418 and airfoil FX77-W-153.

Fig. 9The flap displacement responses of airfoil FX77-W-153 when λ are 2 and 2.6

a)

b)

The flutter extent of airfoil NACA63-418 was much larger than that of the airfoil FX77-W-153. The largest magnitude of the vertical coordinate of time response of airfoil NACA 63-418 reaches almost to 10¹⁴⁷, but the largest magnitude of the vertical coordinate of time response of airfoil FX77-W-153 is almost just 10^-4. In addition, the tip speed ratio region which changes from convergence to divergence and from divergence to convergence is quite narrow and sudden for airfoil NACA63-418. The time response converges when the tip speed ratio is 0.726, but diverges when the tip speed ratio is 0.73. The time response diverges when the tip speed ratio is 2.49 with the magnitude of 10⁶¹ of vertical coordinate but converges when the tip speed ratio is 2.491 just with the magnitude of 10^-5of vertical coordinate. So the changes from convergence to divergence or from divergence to convergence occur suddenly. That is why the flutter of wind turbine blade will occur extremely suddenly and cause extreme danger, and airfoil NACA63-418 is better not to be used for the wind turbine blade. As for the airfoil FX77-W-153, the changes from convergence to divergence or from divergence to convergence are very temperate, because the magnitude of the vertical coordinate of the time response changes very stable. And there is no obvious tip speed ratio of danger for the FX77-W-153.

Therefore, the time domain analysis method can be combined with the eigenvalue approach to predict the flutter region of wind turbine blade and to estimate whether the blade airfoil fits for the design of the wind turbine blade.

6. Conclusions

The eigenvalue approach and the time domain analysis method are utilized respectively to solve the flutter problem of two different wind turbine blade airfoils. The eigenvalue method can determine the flutter region directly by judging whether the real part of the characteristic roots is positive or passive. Based on the four-order Runge-Kutta numerical methods, the time domain analysis of flutter of wind turbine blade is analyzed. The time domain analysis can give the changing tread of the aeroelastic responses in great detail than the eigenvalue approach. For the two different wind turbine blade airfoils, the results of the time domain analysis of the flutter of the blade airfoil can accurately coincides with those of eigenvalue approach. The flap displacement of wind turbine blade airfoil of NACA63-418 will change from convergence to divergence, and change from divergence to convergence extremely suddenly. The flutter will occur suddenly too. And during the flutter region, the flutter will occur dramatically. Therefore, the airfoil NACA63-418 is better not to be used for the wind turbine blade, but the airfoil FX77-W-153 is better for the wind turbine blade.