Validation of bucket wheel drive component model through vibration monitoring: a torque arm key study

1. Introduction

The bucket-wheel excavator is a very dynamic system, with an inherently large number of vibration sources. The bucket wheel drive, or the bucket wheel, is the only assembly that comes into direct contact with the material that is being excavated. It is, therefore, extremely important to extract characteristic oscillation excitation frequencies and natural frequencies. The oscillation modes determine the vibration mode of the bucket wheel drive assembly. Robust monitoring of bucket wheel drive performance requires a combined analysis. The vibration analysis confirms the validity of modeling of the existing and/or optimized design of a component. Validation of the model of a bucket wheel drive component through vibration analysis is based on the proper selection of typical test points, as well as on what the engineer/expert can expect from the definition of the model. The real load acting on the bucket wheel drive, accurately or nearly accurately defines the form of deformation and the main oscillation modes. The first oscillation is largely indicative of the performance of the monitored component.

Many papers [1-4] discuss vibration analysis of rotary systems, including excavator bucket wheel drives. A number of papers [2, 5, 6] present experimental results, whose interpretation is accompanied by the relevant theoretical background. Some papers propose a numerical model based on the finite element method [2, 3, 7, 8]. However, numerical modeling often requires experimental validation, as emphasized in [2, 7, 8]. The validation of the bucket wheel drive component model of excavator SRs1300.26/5+VR, through the vibration analysis discussed in this paper, is based on bucket wheel drive oscillation acceleration diagrams.

2. Vibration as a technical condition parameter of a dynamic system

Vibration is caused by an excitation force, which can either be external or internally generated within the machine itself. The vibration mode is determined entirely by the excitation force and frequency, so vibration analysis can determine the condition of the machine (or diagnose its operation). In its simplest form, vibration represents mechanical harmonic oscillatory motion. However, many dynamic systems are extremely complex in the vibration context, if there are a large number of vibration sources. A dynamic system such as a bucket wheel excavator is not infinitely stiff because it features different degrees of flexibility at different frequencies. It vibrates in response to an external force, depending on the nature of the excitation force and the dynamic characteristics of the mechanical structure. The finite element method is used in analyses that explore how a structure reacts to a known force. However, vibration also represents motion that results in a restitution force. If there are several excitation forces acting simultaneously (or periodically) at different frequencies, the resulting vibration graphic is highly intricate and difficult to interpret. However, regardless of the case, in order to understand the complex vibrations of a bucket wheel excavator, one must begin with linear harmonics, the basic parameters of which are: elongation (displacement) $s$, amplitude $A$, linear frequency $f$, natural (circular) frequency ${\omega }_0$, period $T$, velocity $v$ and acceleration $a$. The correlations between these parameters are well known [5]. Given that ${\omega }_0=2\pi f$, vibration velocity is proportional to frequency since $v_{max}=2\pi fA\text{,}$ and acceleration is proportional to the square of frequency because $a_{max}=4{\pi }^2{f}^{2}A$. This means that a large displacement and high frequency result in high velocity and extremely high acceleration. The vibration amplitude depends on two factors: the amplitude of the excitation force $F$ and the dynamic stiffness of the mechanical system $c_d$, or $A=F/c_d$. The dynamic stiffness of a mechanical system is determined by a set of characteristics such as stiffness $k=m{\omega }_0^2$, mass $m$ and damping $\delta$, with which the bucket wheel excavator counteracts the external force. This means that the oscillation amplitude can increase if the intensity of the excitation force increases or if the dynamic stiffness decreases, or it can decrease if the intensity of the excitation force decreases or the dynamic stiffness increases.

Vibrations represented by a displacement, velocity or acceleration function have different forms but carry the same information. Namely, there are three ways to represent oscillation. The displacement function emphasizes the lowest frequencies, but is difficult to read at higher frequencies. The velocity function is generally uniform at frequency level and is mostly used for machine diagnostics. The acceleration function highlights the highest frequencies, which are of interest in the case of a bucket wheel excavator, so this function was used in the present research.

3. Key study: bucket wheel drive torque arm diagnostics

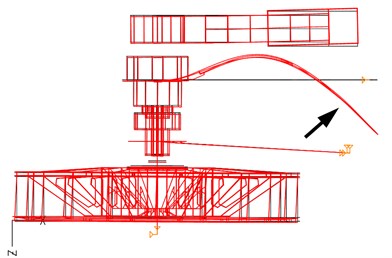
On bucket wheel excavator SRs1300.26/5+VR, which is used for overburden excavation at the Drmno Strip Mine (Kostolac Lignite Basin, East Serbia), the entire bucket wheel drive, including the gearbox, has been replaced. The new 900 kW gearbox, manufactured by the German company Flender, is equipped with a frequency controller. Fig. 1 shows the bucket wheel drive.

Fig. 1Bucket wheel drive of excavator SRs1300

The gearbox, and especially its housing, constitutes an extremely complex assembly, with inter-connected gear pairs, shafts and bearings. Even in the worst-case operating scenario, proper long-term operation of the gearbox requires high stiffness $k$ of the housing. The finite element method enables the determination of stresses and strains through calculations related to complex spatial structures such as gearbox housings. It is the stresses and strains that point to weak structural links that can be eliminated in good time (as early as the design stage), to achieve the required stiffness of the housing. However, there are numerous gearbox optimization requirements in terms of operation. It is a fact that the housing receives and transmits via supports to the boom all the reactive forces and torques generated during the excavation process. Namely, the gearbox has tree supports: two bearings of the gearbox output shaft and one support generally placed in the input shaft zone. One of the basic optimization requirements is the result of this very configuration. The last (third) support needs to be designed and fabricated such that the elastic deformations of the bucket wheel shaft are transmitted to the boom, which is extremely stiff, whereby the gearbox supports should not be subjected to any additional load. Improper housing design, or inadequate supporting, can cause damage to the gearing of the gearbox output shaft.

However, it is a fact that the bucket wheel drive gearbox of excavator SRs1300 features a so-called torque arm, whose function is to transmit the reactive torque generated by the excavation process to the boom before it reaches the gearbox. The housing is thereby largely relieved because the basic load from the gearbox output shaft is directly transferred to the boom support, such that the housing, other than its self-weight, is only loaded by small additional forces. The load goes to the boom structure because the stiffness of the boom is much higher. Fig. 2 is a schematic representation of active and reactive forces.

Fig. 2General schematic of active and reactive forces of a bucket wheel drive

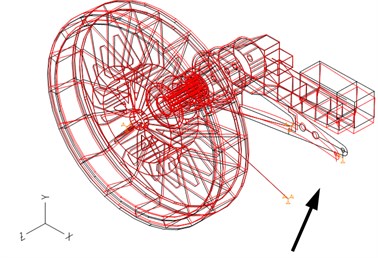
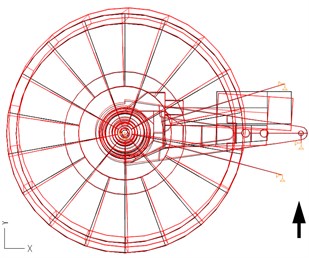
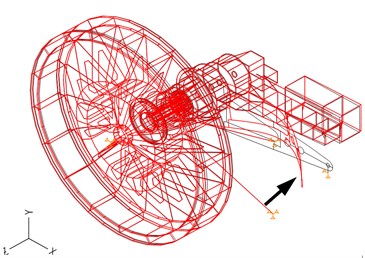
One of the ways to prove that the design of the new drive and torque arm was sound was to develop a mathematical model applying the finite element method and the theory of elasticity. The load of 363 kN declared by the manufacturer corresponds to a torque of 2000 kNm at the bucket wheel; it is transmitted as a reactive force via the torque arm to the structure. Several of the first frequencies, and two characteristic frequencies $f_{11}$ and $f_{12}$, which define the condition and performance of the torque arm (shown in Figs. 3 and 4), were numerically calculated applying the finite element method [2].

Fig. 3Characteristic frequency f11= 17.21 Hz = 1032.6 min-1 – transverse bending of the torque arm

a)

b)

Fig. 4Characteristic frequency f12= 17.22 Hz = 1033.2 min-1 – transverse bending of the torque arm

a)

b)

Transverse bending of the torque arm is another adverse characteristic that dynamic calculations also reveal. The cause of poor performance of the torque arm, which is reflected in the entire excavator drive assembly, is a reactive force.

The validation of (proof for) the poor performance of the torque arm was also obtained experimentally, by recording torque arm vibration acceleration. The measurement was undertaken using instruments and data processing software specially developed for this purpose by the company MikroElektronika from Belgrade. The instruments included a cutting-edge three-component acceleration transducer sensor, an analog/digital signal converter and USB communication with the computer. The frequency signal was derived by FFT analysis, founded upon the Fourier transform. The software supported analysis of time and frequency acceleration signals.

Measurements were performed in three directions (vertical – black line, axial – red line and horizontal – blue line), at three characteristic points (arm support on bucket wheel shaft, middle of arm and arm support on bucket wheel boom structure). The data were measured while the excavator was operating. Typical recorded acceleration signals over time in the three cases are shown in Fig. 5.

Based on the signals shown in Fig. 5, the conclusion was that the lowest acceleration, or displacement or velocity, occurred at the arm support on the bucket wheel shaft. A somewhat higher acceleration rate was recorded at the arm support on the bucket wheel boom structure, and the highest in the middle of the torque arm.

The highest stiffness of the torque arm is achieved at the support of the gearbox output shaft, a somewhat lower stiffness at the support toward the boom, and the lowest stiffness in the middle of the torque arm. The highest elasticity of the torque arm occurs in the middle. At the support of the gearbox output shaft, the torque arm receives all the loads (reactive forces) generated by the excavation process and the operation of the drive assembly (gearbox, electric motor). The increase in the noise caused by excavation (cutting bits going in and out of the excavated material) is depicted in Fig. 5. The amplitudes are small because the stiffness is high.

The middle of the torque arm receives all the loads generated by the excavation forces, but also those coming from the forces produced by the bucket wheel boom. The large amplitudes are a result of the elasticity achieved in the middle of the torque arm, which allows for a certain type of free vibrations with weak damping due to the reactive forces generated by excavation and coming from the boom. This elasticity reduces noise. The increase in the stiffness of the middle of the torque arm (increase in thickness) reduces the elasticity and improves the flow of inner forces to the very stiff component – the bucket wheel boom.

At the support towards the bucket wheel boom, the torque arm receives all the loads coming from the boom (reactive forces of the pulleys, idlers and conveyor belts), but also those generated by the operation of the drive assembly (gearbox, electric motor). The amplitudes are small because of the high stiffness, but still somewhat higher than at the support of the gearbox output shaft. The greater effect of noise due to the rotation of the previously mentioned components (pulleys, idlers) is depicted in Fig. 5.

Fig. 5Vibration acceleration of bucket wheel drive gearbox torque arm over time, recorded at three test points

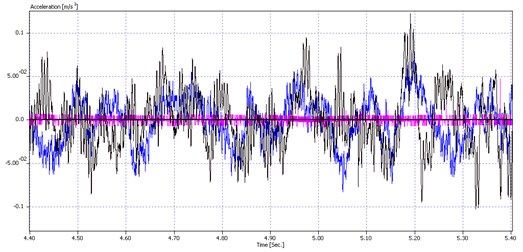
a) Gear reduction output shaft support

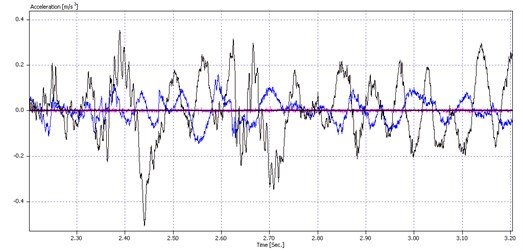
b) Middle of the torque arm

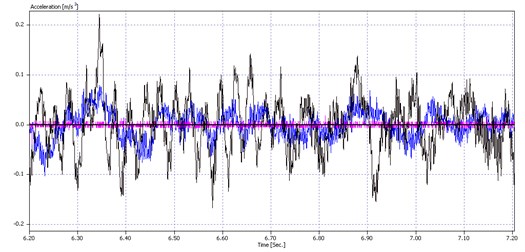
c) Boom structure support

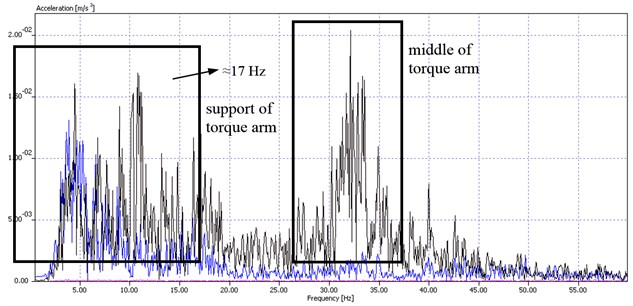
At the torque arm supports, the signals showed that the highest acceleration rate occurred at low frequencies, up to 20 Hz, as opposed to the middle of the torque arm where the highest acceleration rate was in the spectral range from 30 to 40 Hz (Fig. 6).

Vibrations induced by excavation, at a frequency of 2 Hz, exhibit extremely low acceleration. This does not mean, however, that the signal will not be more pronounced when the machine excavates considerably harder material and consequently has to cope with greater resistances. The natural frequencies of the new (replaced) bucket wheel drive assembly, extracted by means of dynamic calculations (shown in Figs. 3 and 4), were related to:

- a poorly sized torque arm (contrary to other components whose stiffness was deemed to be satisfactory);

- the motor support, as part of the structural support of the drive assembly.

The above suggests sound performance of the entire drive assembly. The added RPM controller for the electric motor rotor shaft, or the gearbox input shaft, enables operation over a broad frequency range and allows for excitation variation.

Fig. 6Vibration velocities at a torque arm support and in the middle of the torque arm, at various frequencies

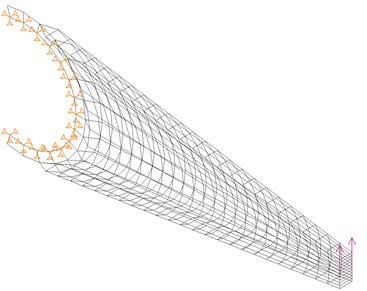
Supporting of the bucket wheel gearbox of excavator SRs1300 vis-a-vis the bucket wheel boom is achieved via the torque arm whose function is to receive reactive forces originating at the bucket wheel during excavation, but also the forces, or oscillations, from the bucket wheel boom. These supports are sinks of sorts, such that the performance of both the supports and the entire drive assembly depends on the geometry and sizing of the torque arm. The bucket wheel torque arm is not stiff enough, and it’s first ($f_{01}=$17.1 Hz) and second ($f_{02}=$17.2 Hz) experimentally determined natural frequencies are extremely close. Since the drive is equipped with a frequency controller, it is highly likely that the first natural frequency (derived from dynamic calculations), will coincide with the excitation from the electric motor rotor shaft RPM, or that of the gearbox input shaft. The solution is to increase the stiffness of the torque arm, or to increase the first natural frequency of the torque arm. By modifying the design of the arm and installing 20 mm-thick dual parallel plates along the entire length of the arm, from one support to the other (creating something like a closed box), the first natural frequency is increased. Fig. 7 shows the proposed reconstruction of the torque arm and its behavior at the first natural frequency.

Fig. 7Proposed design of the torque arm and its behavior at the first natural frequency f01= 30.6 Hz

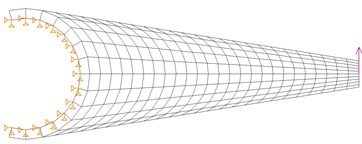
The first natural frequency (in the new design) is considerably higher than the existing frequency (old design), suggesting that a higher level of stiffness is achieved. The consequence of this higher stiffness is that the first natural frequency is also higher, resulting in better overall performance of the drive assembly.

The following conclusions can be drawn from the new solution for the bucket wheel drive assembly of excavator SRs1300, based on dynamic calculations related to the bucket wheel assembly: there are no correlations with excavation frequencies; the model reveals no fractures of the electric motor shaft and gearbox input shaft; and within the operating range of the electric motor, there are undesirable oscillations of the torque arm and electric motor support. Vibrations were measured and analyzed to validate the condition and performance of the torque arm and suggest a potential revitalization approach.

4. Conclusion

The least desirable condition of a structure is the state of resonance, where natural low-frequency vibrations and those induced by external dynamic loading coincide. The component that exhibits technically correct dynamic behavior is that in which the frequency of the first oscillation is high and the interval between adjacent characteristic frequencies large, and vice-versa. Considering the condition and performance of the bucket wheel drive gearbox torque arm, the overall condition of the torque arm was optimized and validated. In order to comply with life cycle and performance requirements for the torque arm, a revitalization approach, based on increasing stiffness, was proposed. Consequently, the first natural frequency of the torque arm is considerably higher and the obtained value is beyond the resonance range.