Health assessment and fault diagnosis for centrifugal pumps using Softmax regression

2.1. Procedures of the methodology

The methodology has two major steps. First is the extraction and selection of features for health assessment and fault diagnosis. The search space is also reduced for fast computation. Second is the use of softmax regression for health assessment and root cause classification.

The process of the methodology can be summarized as Fig. 1.

Fig. 1The process of the methodology

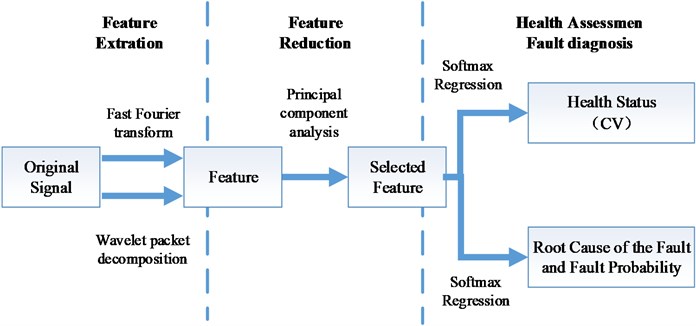
2.2. Feature extraction using wavelet packet decomposition

The fault signals of a centrifugal pump are usually distributed in both high- and low-frequency bands where wavelet packet decomposition can reach a delicate degree. Wavelet packet analysis is a sophisticated method of orthogonal decomposition based on multi-resolution analysis, which can divide the full frequency band of signals in multi-level, so that each band signal contains elaborate information about the original signal. Therefore, wavelet packet decomposition is suitable for extracting both low- and high-frequency features [10-13]. The energy index of all bands reflecting signal characteristics can be constructed by statistically analyzing all bands of signals decomposed by wavelet packet. Determining the scale of wavelet packet decomposition is important. Very low wavelet packet decomposition scale reduces the efficiency of fault feature extraction, whereas very high wavelet packet decomposition scale increases the dimension of feature vector, consequently affecting the calculation rate [14]. Therefore, in centrifugal pump health assessment and fault classification, according to the vibration signal characteristics, the original signal $f\left(t\right)$ can be constructed by the sum of 8 components as Eq. (1), and eight frequency band energy indices $E_{3,j}$ can be calculated by three-layer decomposition:

where $f_8^j\left(t\right)$ is the wavelet packet component signal that can be expressed by a linear combination of wavelet packet functions as:

where $j$ and $k$ are integers and defined as the modulation, scale and translation parameter, respectively;$\mathrm{}{S}_{8,k}^j$ is the wavelet packet coefficients, ${\psi }_{8,k}^j\left(t\right)$ is wavelet packet function:

where $x_{j,k}$ ($j=\text{0,}\text{1,}\text{…}\text{,}\text{7}$; $k=\text{1,}\text{2,}\text{…}\text{,}n$ ) stands for the amplitude of reconstruction signal $S_{3,j}$.

When a centrifugal pump has a fault, the energy of each band signal will have a great impact. Thus, the energy should be normalized into a feature vector $T$:

2.3. PCA-based feature reduction

The PCA procedure employed in this paper will be briefly presented for a more comprehensive data. At a given centrifugal pump operation stage $S$ (in this paper, only the normal machine behavior and machine operation with a worn bearing/impeller are considered), the signal features $X$ are characterized by the multivariate Gaussian distribution with mean ${\stackrel{-}{\mu }}_s$ and the covariance matrix $K_s$. The symmetric matrix $K_s$ can now be represented as:

where $r$ is the rank of the covariance matrix $K_s$, ${\lambda }_i$, $i=\text{1,}\text{2,}\text{...,}r$ are the non-zero eigenvalues of $K_s$, ${\stackrel{-}{\nu }}_i$ are the corresponding unit norm eigenvectors, and:

All eigenvalues of $K_s$ are real and greater than or equal to zero because of its positive semi definiteness. Each eigenvalue ${\lambda }_i$, $i=\text{1,}\text{2,}\text{...,}r$ depicts the amount of the covariance matrix energy projected in the direction of the corresponding eigenvector ${\stackrel{-}{\nu }}_i$ [15]. Only a few of the eigenvalues in $\mathrm{\Lambda }$ account for most of the energy in the covariance matrix $K_s$ when a high degree of correlation exists among the components of $X\text{.}$ Thus, assuming that eigenvalues ${\lambda }_i\text{,}$$i=\text{1,}\text{2,}\text{...,}r$ are arranged in descending order, Eq. (5) can be represented as:

where:

where $p$ is the number of the principal components of $K_s$, ${\lambda }_i$, $i=\text{1,}\text{2,}\text{...,}r$ are the largest $p$ eigenvalues of $K_s$, and ${\stackrel{-}{\nu }}_i$ are the corresponding unit norm eigenvectors.

A query item $\tilde{X}$ can now be transformed into a $p$ component random variable $\tilde{Y}$ given as:

If $\tilde{X}$ belongs to the class of signals from the centrifugal pump state $S$, then $\tilde{Y}$ should be normally distributed with zero mean and variance $I_p$, where $I_p$ is the unity matrix of order $p$. Thus, for each query item $\tilde{X}$, its adherence to the class $S$ can be assessed through the Euclidean norm of the vector $\tilde{Y}$, which in turn corresponds to assessment and classification based on the softmax regression of the query item from the training classes [16].

2.4. Logistic regression method

The machine condition description from daily maintenance records/logs is a dichotomous problem (either normal or failed) that can be represented using an LR function [1]. The goal of logistic regression (LR) is to find the best fitting model to describe the relationship between the categorical characteristics of dependent variables (the probability of an event, constrained between 0 and 1) and independent variables. The logistic function is:

The logistic or logit model is:

where $g\left(x\right)$ is a linear combination of the independent variables $x_1\text{,}{x}_2\text{,}\text{…}\text{,}{x}_k$.

The precondition for figuring out $P\left(x\right)$ is determining parameters $\alpha$ and ${\beta }_1\text{,}\text{…}\text{,}{\beta }_k$ in advance. Dichotomous-dependent variables make estimation using ordinary least squares inappropriate [17]. Hence, estimation in LR chooses the parameters $\alpha$ and ${\beta }_1\text{,}\text{…}\text{,}{\beta }_k$ using the maximum likelihood method rather than those that minimize the sum of squared errors [1]. Then, the probability of failure for each input vector $x$ can be calculated according to Eq. (11).

2.5. Softmax regression method

In the softmax regression setting, multi-class classification (as opposed to only binary classification) is interested, and so the label $y$ can take on $k$ different values, rather than only two. Thus, in training set $\left\{\right(x^{\left(1\right)},y^{\left(1\right)}),\dots ,(x^{\left(m\right)},y^{\left(m\right)}\left)\right\}$ , we now have that $y^{\left(i\right)}\in \{\mathrm{1,2},\dots ,k\}$ .

Given a test input $x$, the hypothesis to estimate the probability that $p(y=j|x)$ for each value of $j=\text{1,}\text{2,}\text{...,}k$ is wanted. I.e., the probability of the class label taking on each of the $k$ different possible values is estimated. Thus, the hypothesis will output a $k$ dimensional vector (whose elements sum to 1) giving $k$ estimated probabilities [18].

Concretely, our hypothesis $h_{\theta }\left(x\right)$ takes the form:

Here ${\theta }_1,{\theta }_2,\dots ,{\theta }_k\in {\mathfrak{R}}^{n+1}$ are the parameters of the softmax regression model. Notice that the term $1/{\sum }_{j=1}^k{e}^{{\theta }_j^T{x}^{\left(i\right)}}$ normalizes the distribution, so that it sums to one.

In the special case where $k=$2, softmax regression reduces to logistic regression. This shows that softmax regression is a generalization of logistic regression. The cost function used for softmax regression is:

where $1\{·\}$ is the indicator function, so that $1\left\{\text{a}\text{true statement}\right\}=\text{1,}$ and $1\left\{\text{a false statement}\right\}=\text{0}$.

There is no known closed-form way to solve for the minimum of $J\left(\theta \right)$, and thus as usual well resort to an iterative optimization algorithm such as gradient descent or L-BFGS. Taking derivatives, the gradient is:

Softmax regression has an unusual property that it has a “redundant” set of parameters. Adding weight decay to the cost function is needed. This will take care of the numerical problems associated with softmax regression's overparameterized representation.

The modified cost function is:

The derivative of the modified cost function is:

By minimizing $J\left(\theta \right)$ with respect to $\theta$, a working implementation of softmax regression is given.

3.1. Data acquisition system description

Three vibration signals were acquired from an installed accelerometer, with a sampling rate of 10.24k Hz.

3.2. Feature extraction and reduction

FFT was used for each vibration signal to obtain the fundamental frequency amplitude. Three-level wavelet packet decomposition using Daubechies wavelet (DB10) was adopted for each vibration signal, and fundamental frequency amplitude and packet energies were used as features. A subset of feature components was determined using PCA. In this case, a four-dimensional feature vector was finally selected as a feature vector for health assessment and fault mode classification after feature reduction.

3.3. Softmax regression models training

• Softmax regression model trained for health assessment.

When Softmax regression model was trained for health assessment, softmax regression reduced to logistic regression. A total of 120 sets of data were used as training data, including 40 sets of data sampled under normal conditions [$P\left(x\right)=$0] versus 80 sets of fault data [$P\left(x\right)=$1]. The parameters $\alpha$ and ${\beta }_1\text{,}\text{…}\text{,}{\beta }_4$ were estimated using the maximum likelihood method to eventually obtain the model for performance assessment as softmax regression model 1.

• Softmax regression model trained for fault diagnosis.

Four fault modes of the centrifugal pump which include bearing roller wearing, bearing inner race wearing, bearing outer race wearing and centrifugal pump impeller wearing, were considered. Four sets of centrifugal pump vibration data (one set for each fault mode of the centrifugal pump) were used for training centrifugal pump fault diagnosis model based on softmax regression.

Set 1 (bearing roller wearing): 40 subsets of bearing roller wearing data ($p(y=1|x)=\text{1}$) versus 40 subsets of non-wearing data ($p(y=1|x)=\text{0}$);

Set 2 (bearing inner race wearing): 40 subsets of bearing inner race wearing data ($p(y=2|x)=\text{1}$) versus 40 subsets of non-wearing data ($p(y=2|x)=\text{0}$);

Set 3 (bearing outer race wearing): 40 subsets of bearing outer race wearing data ($p(y=3|x)=\text{1}$) versus 40 subsets of non-wearing data ($p(y=3|x)=\text{0}$);

Set 4 (centrifugal pump impeller wearing): 40 subsets of centrifugal pump impeller wearing data ($p(y=4|x)=\text{1}$) versus 40 subsets of non-wearing data ($p(y=4|x)=\text{0}$).

The parameters ${\theta }_1\text{,}{\theta }_2\text{,}\text{…}\text{,}{\theta }_k$ were estimated using gradient descent method to eventually obtain the model for fault diagnosis as softmax regression model 2.

3.4. Validation

Four sets of centrifugal pump vibration data (one set for each fault mode) were used for validation of centrifugal pump health assessment and fault diagnosis models based on softmax regression.

• Set 1 (bearing roller wearing): 10 data under normal condition versus 40 bearing roller wearing data;

• Set 2 (bearing inner race wearing): 10 data under normal condition versus 32 bearing inner race wearing data;

• Set 3 (bearing outer race wearing): 10 data under normal condition versus 40 bearing outer race wearing data;

• Set 4 (centrifugal pump impeller wearing): 10 data under normal condition versus 30 impeller wearing data.

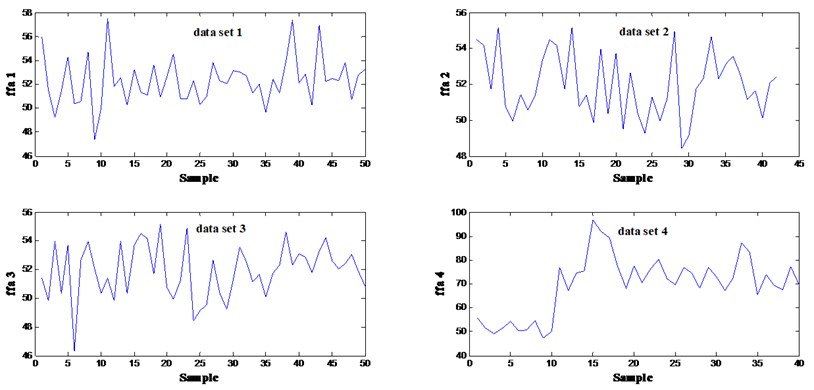
FFT and three-level wavelet packet decomposition using Daubechies wavelet (DB10) were adopted for extracting features from four sets of validation data. The wavelet package energies (E0 to E7) extracted from data set 1 to 4 is respectively show in Figs. 3-6. The fundamental frequency amplitude (or ffa, for short) extracted from data set 1 to 4 (ffa 1, ffa 2, ffa 3 and ffa 4) is show in Fig. 7.

Fig. 3The wavelet package energies extracted from data set 1

Fig. 4The wavelet package energies extracted from data set 2

Fig. 5The wavelet package energies extracted from data set 3

Fig. 6The wavelet package energies extracted from data set 4

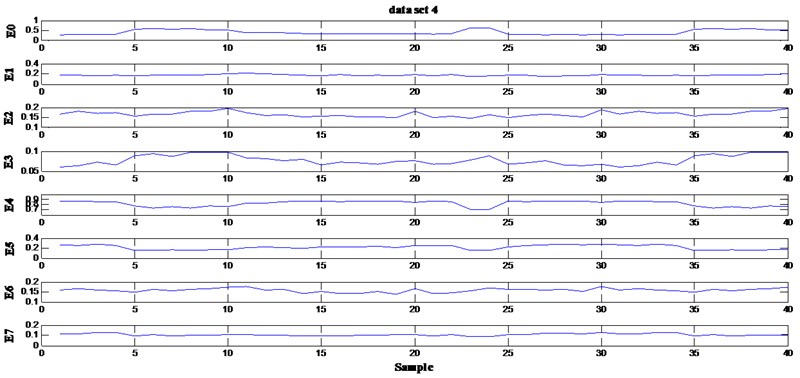
Fig. 7The fundamental frequency amplitude extracted from data set 1 to 4

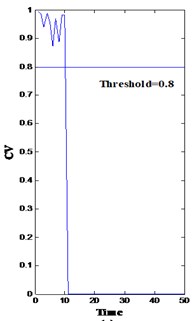
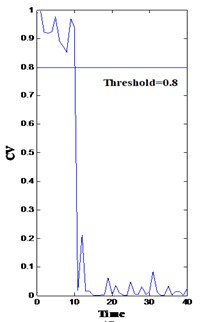
Reduced features are input into softmax regression models to assess the centrifugal pump health condition and identify possible failure modes. The confidence value ($CV$) was calculated based on the probability of failure. Define $CV=1-P\left(x\right)$. When the centrifugal pump operates normally, $CV$ is close to 1; if the centrifugal pump is going to fail, $CV$ is approaching 0 correspondingly; If the confidence value is less than a predetermined threshold (e.g., 0.8), the root fault diagnosis module will be triggered, and features are input into fault diagnosis models to calculate the probability of each fault.

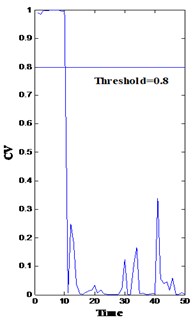
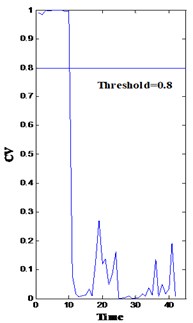
Fig. 8(a)-(d) show the overall health assessment of the four sets of centrifugal pump vibration data using model softmax regression model 1. The probability of different fault modes conducted from softmax regression model 2 is shown in Fig. 9(a)-(d).

Fig. 8Health assessment result of four fault modes

a)

b)

c)

d)

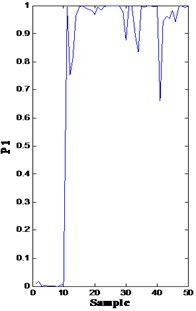
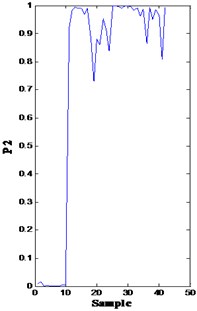
In Fig. 8, both bearing and impeller problems can be detected from the $CV$ drops. However, the difference among the four drops and their cause are difficult to clarify. In this methodology, the fault diagnosis module is triggered as long as the confidence value is below a predetermined threshold (0.8) by inputting the corresponding features into the trained models (the softmax regression model 2) to calculate the probability of fault modes. From time 10, the probability of fault mode 1 (bearing roller wearing, p1), fault mode 2 (bearing inner race wearing, p2), fault mode 3 (bearing outer race wearing, p3), and fault mode 4 (impeller wearing, p4) is very high [solid line in Fig. 9(a)-(d), respectively]. Consequently, the minor probability of the failure of these points is indicated in Fig. 9.

Fig. 9Probability of fault modes 1, 2, 3, and 4

a)

b)

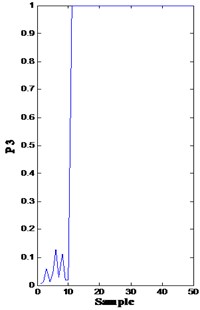
c)

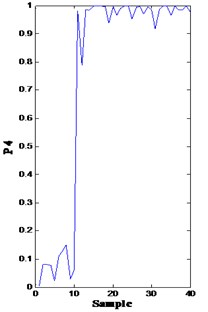
d)

In conclusion, a softmax classifier is more suitable for centrifugal pump fault diagnosis than 4 separate binary classifiers using logistic regression. The four fault modes considered in this paper are mutually exclusive, so softmax regression classifier would be appropriate. Besides that, softmax regression is more simple, useful and easy to implement.