Deformation-compensated modeling of flexible material processing based on T-S fuzzy neural network and fuzzy clustering

Deng, Yaohua; Chen, Sicheng; Chen, Jiayuan; Wu, Jiayi; Zhang, Qiaofen; Wu, Liming; Chen, Hui

Journal of Vibroengineering

Browse Journal

Submit article

Published: 15 May 2014

Check for updates

Deformation-compensated modeling of flexible material processing based on T-S fuzzy neural network and fuzzy clustering

Yaohua Deng¹

Sicheng Chen²

Jiayuan Chen³

Jiayi Wu⁴

Qiaofen Zhang⁵

Liming Wu⁶

Hui Chen⁷

^{1, 2, 3, 4, 5, 6, 7}Guangdong University of Technology, Guangzhou, Guangdong, China

Corresponding Author:

Yaohua Deng

Cite the article Download PDF

Downloads 1097

Abstract

According to the factors that influence flexible material processing (FMP), the deformation compensation modeling method based on T-S fuzzy neural network is proposed. This method combines T-S fuzzy reasoning with a fuzzy neural network. Firstly, fuzzy clustering is introduced to extract fuzzy membership functions and the fitness of fuzzy rules of T-S fuzzy neural network antecedent from the past processing data. Secondly, with the steepest descent method, back-propagation iteration is used to calculate the connection weights of the network. The processing of experiments shows that T-S fuzzy neural network modeling is superior to typical T-S model. The angle error and the straightness error processed by NTS-FNN is 40.4 %, 28.8 % lower than those of STS-FNN. The minimum processing time processed by NTS-FNN is lower by 46.1 % than that of STS-FNN.

1. Introduction

The flexible material processing (FMP) refers to the process that takes various complex graphical processing on a flexible material (combined by multi-layer soft material), and an uneven three-dimensional pattern strayed on the surface of a flexible material [1, 2].

FMP deformation can be caused by multiple factors. Generally, several relevant variables will be regulated in order to reduce processing errors. Essentially, the compensation control of FMP deformation is a multi-input and a multi-output process. At present, the intelligent modeling of FMP is mainly based on the method of regression analysis, fuzzy reasoning and neural network [3, 4]. The method of Neural Network PLSR (NNPLSR) [5]; Kernel PLSR (KPLSR), which is suitable for real-time process modeling, is studied in [6-7]. Regarding the methods of modeling artificial intelligence, in 1993, a Japanese scholar Yasukawa proposed a simplified T-S fuzzy model. Its parameter of conclusion is expressed by a single value, which greatly simplifies the identification process [8]. In 1996, another Japanese scholar Sugeno proposed a T-S fuzzy model of a continuous recognition algorithm, the model parameter adjustment is achieved by the least squares method of weighted round robin [9]. In 2002, S. G. Cao from Australia proposed a fuzzy dynamic model, which consisted of multiple linear equations that smoothly connected global models through fuzzy membership functions. The accuracy of approximation can be arbitrary to any continuous nonlinear functions, which are defined on the compact set [10]. In 2011, Uros Zuperl from Slovenia studied the neural network model cutting force prediction of 3D spherical milling process [11].

Through the analysis of the literature above, it can be concluded that fuzzy, neural network modeling method has a strong non-linear expression. It is suitable for dynamic and complex uncertainty process modeling. A primitive angle, the interpolation rate, the processing direction angle and the flexible parts clamping way influence FMP deformation. Furthermore, some problems exist in the actual machining process, which requires deformation compensation prediction in real-time.

This paper proposes the FMP deformation compensation modeling, which effectively combines T-S fuzzy reasoning and a fuzzy neural network. It also introduces fuzzy clustering in order to achieve antecedent network model identification [12]. Based on fuzzy clustering, it adaptively adjusts the input space clustering center, the radius and the number of clusters, completes the input space fuzzy classification, determines the membership function and the rule fitness of data points, and improves the model training speed and approximation accuracy.

2. FMP deformation compensation modeling based on T-S fuzzy neural network

As the consequent network structure of a typical T-S model is relatively simple, if a new hidden layer is added to the consequent network, it will contribute to improve the universal approximation capacity of the model. Fig. 1 shows a new T-S fuzzy neural network extended model diagram of the standard T-S model. An antecedent network and a consequent network construct the new T-S fuzzy neural network model. The antecedent network is used to match the premise of T-S fuzzy rules. Meanwhile the consequent network generates the fuzzy rules. Then, the non-linear relationship modeling between the compensation output $S = {s_{1}, s_{2}, \dots, s_{r}}$ and the deformation factors $X = {x_{1}, x_{2}, \dots, x_{n}}$ is established through weighted calculations of antecedent and consequent networks.

Fig. 1Construction of T-S fuzzy neural network model after extension

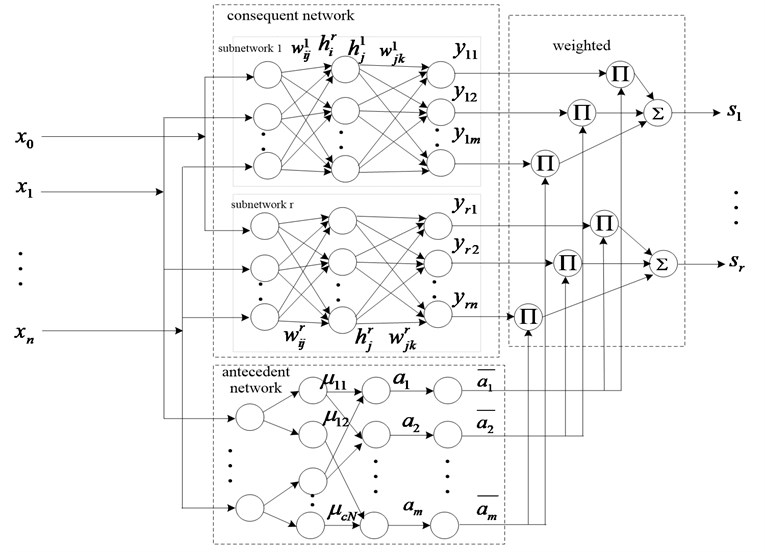
2.1. FMP deformation compensation model constructed by T-S fuzzy neural network

In Fig. 1, the T-S fuzzy neural network structure of FMP deformation compensation includes the function of a structuring membership, the rules of fitness of an antecedent network, and the calculations of the weight parameter of a consequent network [4].

2.1.1. Constructed antecedent network through clustering division of input data

The purpose of the division of FMP input data (FMP deformation influence factors) is to divide the input data fuzzy level, and to identify the coordinates of the center of each clustering and the width of each division district. Introducing the front part of the antecedent of T-S fuzzy neural network extracts input membership functions and the fitness of the fuzzy rules. Fuzzy clustering of the input data is mainly for working out the fuzzy partition matrix and clustering centers. Fuzzy clustering distance measurements are shown by Mahalanobis distance by calculating the minimum objective function (Eq. (1)) of $c$ groups of fuzzy clustering division. This is done in order to obtain the data point $x_{k}$ ’s clustering centers and the fuzzy partition matrix:

1

M i n \{J (X; U, V)\} = \sum_{i = 1}^{c} \sum_{k = 1}^{N} {(u_{i k})}^{β} D_{i k M_{i}}^{2} .

In Eq. (1): $X = {x_{1}, x_{2}, . . ., x_{n}}$ is the $n$ -dimensional input data set. $U = [u_{i k}]$ is the fuzzy partition of $X (u_{k})$ is a $k$ -th sample that about $i$ -th class membership degree), and $\sum_{i = 1}^{c} u_{i k} = 1$ , $k =$ 1, 2,…, $N$ . $D_{i k M_{i}}^{2}$ is the square inner product from the mid-point of $n$ -dimensional data space $x_{k}$ to clustering center $v_{i}$ (Eq. (2)):

2

D_{i k M_{i}}^{2} = {(x_{k} - v_{i})}^{T} M_{i} (x_{k} - v_{i}) .

In Eq. (2), $M_{i} = d e t {(F_{i})}^{\frac{1}{n}} F_{i}^{- 1}$ , where $F_{i}$ is a positive definite symmetric matrix:

3

F_{i} = \frac{\sum_{k = 1}^{N} {(u_{i k})}^{β} (x_{k} - v_{i}) {(x_{k} - v_{i})}^{T}}{\sum_{k = 1}^{N} {(u_{i k})}^{β}} .

In Eq. (1), the minimum objective function is the basis for input data fuzzy clustering. Meanwhile, $\sum_{i = 1}^{c} u_{i k} = 1$ , $k =$ 1, 2,…, $N .$ Eq. (1) use Lagrange multiplier method to get the objective function and constrains. Then, introduced Lagrange multiplier $λ$ :

4

M i n \{\bar{L} (X; U, V, λ)\} = \sum_{i = 1}^{c} \sum_{k = 1}^{N} {(u_{i k})}^{β} D_{i k M_{i}}^{2} + \sum_{k = 1}^{N} λ_{k} (\sum_{i = 1}^{c} u_{i k} - 1) .

The requirement for getting the extreme of $\bar{L} (X; U, V, λ)$ is:

5

\{\begin{array}{l} \frac{\partial \bar{L}}{\partial μ_{i k}} = [β {(μ_{i k})}^{β - 1} {(D_{i k M_{i}})}^{2} + λ] = 0, \\ \frac{\partial \bar{L}}{\partial v_{i}} = \sum_{k = 1}^{N} {(μ_{i k})}^{β} \frac{\partial}{\partial v_{i}} [{(x_{k} - v_{i})}^{T} M_{i} (x_{k} - v_{i})] = 0, \\ \frac{\partial \bar{L}}{\partial λ} = (\sum_{i = 1}^{c} u_{i k} - 1) = 0, 1 \leq i \leq c, 1 \leq k \leq N, \end{array} \Rightarrow \{\begin{array}{l} u_{i k} = \frac{1}{\sum_{j = 1}^{c} {(\frac{D_{i k M_{i}}}{D_{j k M_{j}}})}^{\frac{2}{β - 1}}}, \\ v_{i} = \frac{{\sum_{k = 1}^{N} (u_{i k})}^{β} x_{k}}{\sum_{k = 1}^{N} {(u_{i k})}^{β}} . \end{array}

Therefore, if the values of data set $X$ , the categories number of clustering $c$ , and the fuzzy weighting exponent $β$ are known, the data partitioning, the optimal fuzzy classification matrix and the cluster center all can be calculated by Eq. (5) [13].

Suppose the fuzzy partition matrix of input data is $U = [u_{i k}]$ after the fuzzy clustering division, the fuzzy category of $c$ set is $G_{i}$ (1 $\leq i \leq c$ ), then categories’ center of $G_{i},$ $v_{i q},$ and the corresponding variance $σ_{i q}^{2}$ can be:

6

v_{i q} = \frac{\sum_{k = 1}^{N} {(u_{i k})}^{β} q_{k}}{\sum_{k = 1}^{N} {(u_{i k})}^{β}}, σ_{i q}^{2} = \frac{\sum_{k = 1}^{N} {(u_{i k})}^{β} {(q_{k} - v_{i q})}^{2}}{\sum_{k = 1}^{N} {(u_{i k})}^{β}} .

If the input data space division requires a high fuzzy clustering, in each $G_{i}$ category data $q_{k}$ is very close to the category component of $v_{i, n + 1}$ ( $i = 1, 2,..., c$ ) of the clustering center $V_{i} = {[v_{i, 1}, v_{i, 2}, . . ., v_{i, n + 1}]}^{T}$ (variance is $σ_{i q}^{2} \approx 0$ ), the clustering center corresponds to $G_{i}$ , then the category value $q_{k}$ , which is the shortest distance from the categories’ center $v_{i q}$ can be used as the decision function $D (G_{i})$ :

7

D (G_{i}) = {q_{k} | m i n (| q_{k} - v_{i q} |)} .

Corresponding, relative to $G_{i}$ membership function of $x_{k}$ is presented in Eq. (8), where $i = 1, 2,..., c$ , $j = 1, 2,..., n$ , $| v_{i q} - v_{i q}^{'} |$ is the width of the corresponding input data division region. $v_{i q}^{'}$ is the value of the cluster center, which is closest to the center of the $i$ -th cluster. $γ$ reflects the coefficient of the membership reduction speed when the input sample is away from the cluster center:

8

Z_{j i} (x_{k j}) = E x p (- \frac{|x_{k j} - v_{i q}|}{|v_{i q} - v_{i q}^{'}|} \times γ) .

The physical meaning of the membership function $Z_{j i} (x_{k j})$ can be described as a measuring of a similar relationship between the input sample $x_{k}$ and the fuzzy category $G_{i}$ ’s prototype. If $x_{k}$ is away from the prototype, $Z_{j i} (x_{k j})$ is closer to 0. If $x_{k}$ is closer to prototype, $Z_{j i} (x_{k j})$ moves near 1 [4].

For each fuzzy category $G_{i}$ and its decision category, $R_{i}$ reflects one of the decision rules ( $R_{i} :$ if $x_{k} \in G_{i}$ , then $d (x_{k}) = D (G_{i})$ , $i = 1, 2,..., c$ ). If the multidimensional fuzzy set $G_{i}$ is projected to the whole input data space, then the decision rule $R_{i}^{'}$ is as follows:

9

R_{i}^{'} : i f x_{1} \in G_{i 1} and x_{2} \in G_{i 2} and…and x_{n} \in G_{i n}, then d (x_{k}) = D (G_{i}) .

Respectively, the rule fitness of $x_{k}$ , relative to the rules of $R_{i}^{'}$ , is expressed by Eq. (10):

10

υ_{i} = \prod_{j = 1}^{n} Z_{j i} (x_{k j}), i = 1,2, . . ., c .

Eqs. (8) and (10) are the calculation formula of the membership function and rule fitness when constructing the T-S fuzzy neural network model. Therefore the constructing of T-S fuzzy neural network model follows the below steps: 1) The execution of the fuzzy clustering algorithm in input data space to get category $G_{i}$ ( $1 \leq i \leq c$ ); 2) The category center $v_{i q}$ , corresponding to the variance $σ_{i q}^{2}$ of all fuzzy categories is calculated (by using Eq. (6)); 3) By using the quality indicators parameter $ξ$ , an excellent divided fuzzy category is selected; 4) The fuzzy category decision function $D (G_{i})$ after a filter is calculated (by using Eq. (7)); 5) The membership $Z_{j i} (x_{k j})$ of sample data $x_{k}$ with respect to the fuzzy category $G_{i}$ is calculated; 6) Fuzzy rule sets are generated according to Eq. (9); rule fitness $υ_{i}$ are computed according to Eq. (10).

$ξ$ is introduced as the parameter of the quality standard. Firstly, it assigns one small value to $c$ , calculating all variance of fuzzy division categories. If $σ_{i q}^{2} > ξ$ , $c = c + 1$ , then the fuzzy partition is redone and looped until the condition $σ_{i q}^{2} \leq ξ$ is met. Only then the corresponding fuzzy categories are accepted to construct a membership of a fuzzy neural network model.

2.1.2. Calculation of consequent network parameters $w_{i j}^{r}$ , $w_{j k}^{r}$

The value of the consequent network parameters $w_{i j}^{r}$ and $w_{j k}^{r}$ are calculated based on the steepest descent learning algorithm. Supposed, $S_{r} = {[s_{1}, s_{2}, \dots, s_{r}]}^{T},$ $S_{r}^{'} = {[s_{1}^{'}, s_{2}^{'}, \dots, s_{r}^{'}]}^{T}$ represent the actual and the expected outputs of the consequent neural network. Then, the network output minimum variance of error cost function is $E_{m s e} = \frac{1}{2} \sum_{r = 1}^{p} {(s_{r}^{'} - s_{r})}^{2}$ .

Moreover, supposed $Δ E_{m s e} = \frac{\partial E_{m s e}}{\partial w}$ , $W$ represents the connection weights between nodes, $u \in (0,1)$ is learning rate, neurons coefficient iterative function each layer of consequent neural network is $W (t + 1) = W (t) - u Δ E_{m s e}$ , and calculated by the error back-propagation algorithm, the calculation formulas of $w_{j k}^{r}$ and $w_{i j}^{r}$ are:

11

w_{j k}^{r} (t + 1) = w_{j k}^{r} (t) + u (s_{r}^{'} - s_{r}) \bar{a_{j}} h_{j}^{r},

12

w_{i j}^{r} (t + 1) = w_{i j}^{r} (t) - u (s_{r}^{'} - s_{r}) \bar{a_{j}} w_{j k}^{r} ∙ e^{- \sum_{i} w_{i j}^{r} x_{i}} {(\frac{1}{1 + e^{- \sum_{i} w_{i j}^{r} x_{i}}})}^{2} x_{i} .

3. Processing test experiments

Real measure data of FMP is taken to test the performance of the new deformation compensation model T-S fuzzy neural network (below called NTS-FNN), which was discussed above. The analysis and the calculation is carried out with Intel i5 processor, 2.4 GHz frequency, 2 GB RAM, Microsoft Windows 7 Professional operating system, and MATLAB R2008 software platform.

3.1. Modeling of FMP deformation compensation

The primitive angle $x_{1}$ (°); the feed depth $x_{2}$ (mm); primitive types (circle or line) $x_{3}$ (circle: 1, line: 2); the processing step $L_{s t e p}$ (mm) $x_{4}$ as the deformation influence factors (which are the input parameters of NTS-FNN) are taken, and $s_{1}$ , $s_{2}$ are taken ass the feed compensation parameters of the $X$ , $Y$ direction (which are the output of NTS-FNN) in order to construct NTS-FNN model. This mainly includes: 1) Construction of the antecedent network membership function $Z_{j i} (x_{k j})$ , the fuzzy rule fitness $υ_{i}$ ; 2) Calculation of $w_{j k}^{1}$ , $w_{i j}^{1}$ , $w_{j k}^{2}$ , $w_{i j}^{2}$ of consequent network parameter.

Fig. 2Experiment platform of quilting CNC

Choose five pieces of flexible parts, which length and width is 200 mm×120 mm and the material is polyurethane foam (the modulus of elasticity $E =$ 0.3652 MPa, Poisson’s ratio $μ =$ 0.25). Flexible parts have different thickness. The track machining experiment was conducted on the quilting CNC platform (Fig. 2), and the track angle machining error was controlled within ±2.0 %. 265 samples were gained (flexible parts’ thickness (mm) is 5, 15, 20, 25, 35, the machining track is parallelogram, cure angle is 15°, 30°, 45°, 60°) as test data of NST-FNN.

Assigned $β = 2$ , $ε = 0.00001,$ maximum iteration number $t_{m a x} =$ 400, $c =$ 2, $ξ = 1.3 .$ According to Eq. (8), assigned $γ = 2$ , membership function $Z_{j i} (x_{k j})$ and the fuzzy rule fitness $υ_{i}$ of $x_{1}$ - $x_{4}$ are gained. Furthermore, the number of nodes of each layer of the antecedent network is determined: from 1 to 4 is 4, 40, 10, 10. Finally, according to the Hecht-Nielsen method, it is confirmed that each layer neurons nodes of antecedent network is 4-40-10-10, consequent network is 5-11-10-2.

233 samples are chosen from the original 265 samples to train consequent network. 32 samples are left for the accuracy test, at the learning efficiency initial value $u =$ 0.4, the minimum expected error $e_{m i n} =$ 0.001. The training step is 600, the gain consequent network parameter is $w_{i j}^{2}$ :

w_{i j}^{2} = [\begin{matrix} 0.8633 0.0689 0.7072 0.2858 \\ - 0.4793 1.3544 - 1.0627 - 1.0783 \\ 0.2536 0.1617 0.8223 0.9368 \\ 0.7743 0.1499 0.7620 0.6371 \\ 0.6775 0.7475 0.0382 0.8506 \\ 0.5162 1.5871 0.4567 0.0952 \\ 0.7334 0.5066 0.3355 0.9308 \\ - 0.0908 0.8941 0.3813 0.6295 \\ 0.6717 0.1603 0.3879 0.5664 \\ 0.1247 1.7480 0.3613 0.5867 \\ - 0.6101 1.1671 - 0.7069 - 0.6300 \end{matrix}] .

Furthermore, $w_{i j}^{1}$ , $w_{j k}^{1}$ , $w_{j k}^{2}$ is calculated.

3.2. Processing experiments

The processing track angle error $f_{α}$ , the straightness error $f_{l}$ , and the primitive minimum processing time $t_{p}$ are chosen as the machining performance test indicators. Moreover, performance indicators are compared to the standard-based fuzzy neural network prediction model STS-FNN [4].

Fig. 3Processing track geometry

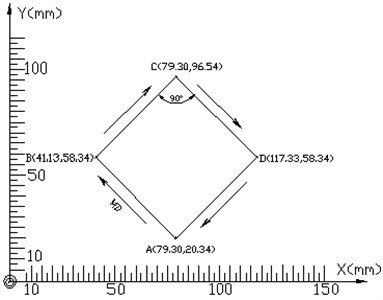
The pattern in Fig. 3 is used as the processing track, polyurethane sponge is used as a flexible material (the modulus of elasticity $E =$ 0.3652 MPa, Poisson’s ratio is 0.25), length, width and height of the flexible material is 150 mm×100 mm×15 mm. The processing experiment is without precompensation (NC), the feedback compensation control based on STS-FNN or NTS-FNN is conducted separately.

1) Process of errors $f_{α}$ , $f_{l}$

Under the control of STS-FNN and NTS-FNN respectively, 14 groups processing samples are received. After data treatment, 3 groups of samples are removed (those with the starting points and end points not closed). Finally, 11 groups samples are selected to respectively measure the processing track angle errors and the straightness errors.

Fig. 4 shows a comparative graph of processing errors of the processing track angle error $f_{α}$ , the straightness error $f_{l}$ (that without precompensation (NC), and with compensation by STS-FNN, NTS-FNN). Processing track angle error: $f_{a - N C}^{}$ , $f_{a - S T S F N N}^{}$ , $f_{a - N T S F N N}^{}$ ; straightness error: $f_{l - N C}^{}$ , $f_{l - S T S F N N}^{}$ , $f_{l - N T S F N N}^{}$ .

Fig. 4Comparative graph of processing errors

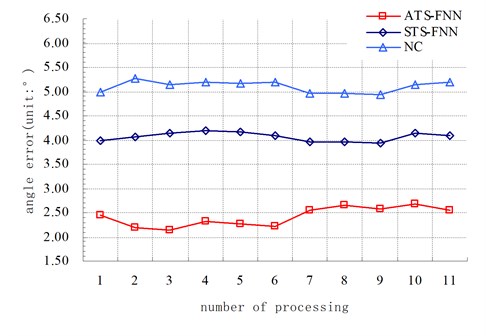
a) $f_{a - N C}^{}$ , $f_{a - S T S F N N}^{}$ , $f_{a - N T S F N N}^{}$

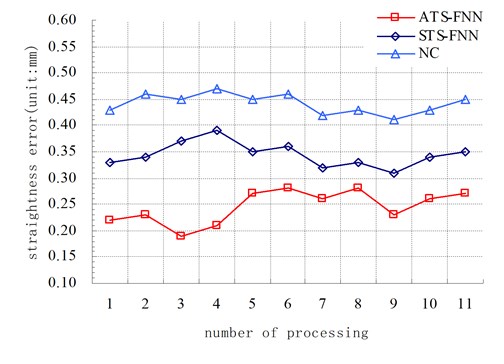
b) $f_{l - N C}^{}$ , $f_{l - S T S F N N}^{}$ , $f_{l - N T S F N N}^{}$

Furthermore, more calculations are made: the processing track angle error of the average without precompensation (NC), compensation by STS-FNN, NTS-FNN are: $f_{a - N C}^{'} =$ 5.09°, $f_{a - S T S F N N}^{'} = 4.06°,$ $f_{a - N T S F N N}^{'} = 2.42°;$ average straightness errors are: $f_{l - N C}^{'} =$ 0.44 mm, $f_{l - S T S F N N}^{'} =$ 0.34 mm, $f_{l - A T S F N N}^{'} =$ 0.25 mm.

2) Primitive minimum processing time $t_{p}$

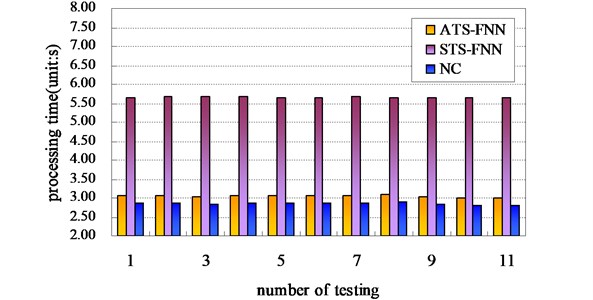
From the testing results shown in Fig. 5, the time-consuming of completing track processing is as below.

The average primitive minimum processing time of process without pre-compensation (NC) $t_{p - N C} =$ 2.86 s; with feedback compensation control based on STS-FNN $t_{p - S T S F N N} =$ 5.66 s; based on NTS-FNN $t_{p - A T S - F N N} =$ 3.05 s.

From the processing experiment results, we can conclude that the processing track on the flexible material of thickness is 15 mm, $f_{a - N T S F N N}^{'}$ is 40.4 %, 52.55 % smaller than $f_{a - S T S F N N}^{'}$ , $f_{a - N C}^{'}$ ; $f_{l - N T S F N N}^{'}$ decreased 28.8 %, 44.45 % relative to $f_{l - S T S F N N}^{'}$ , $f_{l - N C}^{'}$ ; $t_{p - N T S F N N}$ decreased 46.1 % relative to $t_{p - S T S F N N}$ , and increased by 6.65 % more than $t_{p - N C}$ .

Fig. 5Comparative graph of primitive minimum processing time

4. Conclusion

1) In the T-S fuzzy neural network modeling process, pre-optimized input spaces (by using the fuzzy clustering method) ensure an antecedent network membership function, simplify the fuzzy rule number, help save fuzzy reasoning time, and improve model training speed. The testing result shows that the primitive minimum processing time processed by NTS-FNN is lower by 46.1 % than that processed by STS-FNN.

2) FMP deformation compensation modeling method includes the advantage of fuzzy clustering and T-S fuzzy neural network method. Compensated by NTS-FNN, an angle error, the straightness error is 40.4 %, which is 28.8 % lower than these of STS-FNN.

3) The consequent network and the antecedent network are relatively independent. Therefore they can easily realize embedded parallel computing. This is conducive to the application of the model in the prediction of the actual FMP compensation.

References

Yaohua Deng, Sicheng Chen, Bingjing Li, Jiayuan Chen, Liming Wu Study and testing of processing trajectory measurement method of flexible workpiece. Mathematical Problems in Engineering, Vol. 2013, 2013.

Search CrossRef
Yaohua Deng, Bingjing Li, Sicheng Chen, Jiyuan Chen Deformation forecast of flexible material process by spline finite element method and application. International Journal on Smart Sensing and Intelligent Systems, Vol. 6, Issue 1, 2013, p. 333-351.

Search CrossRef
Sun Zengqi, Xu Hongbin Fuzzy-neural network based on T-S model. Journal of Tsinghua University, Vol. 37, Issue 3, 1997, p. 76-80.

Search CrossRef
Deng Yaohua Liu Guixiong ATS-FNN-based modeling and simulation for compensation prediction of fwp machining deformation. Journal of South China University of Technology, Natural Science Edition, Vol. 40, Issue 3, 2012, p. 146-151.

Search CrossRef
J. M. Karthikeya Udayagiri V. R.,Taleb Moazzeni, et al. Detection algorithms for the Nano Nose. 19th International Conference on Systems Engineering, 2008, p. 399-404.

Search CrossRef
Kyungpil Kim, Jong-Min Lee, In-Beum Lee A novel multivariate regression approach based on kernel partial least squares with orthogonal signal correction. Chemometrics and Intelligent Laboratory System, Vol. 79, 2005, p. 22-30.

Search CrossRef
Bai Yifeng, Xiao Jian, Yu Long Kernel partial least-squares regression. International Joint Conference on Neural Networks, 2006, p. 1231-1238.

Search CrossRef
Sugeno M., Yasukawa T. A fuzzy logic based approach to qualitative modeling. IEEE Trans on Fuzzy Systems, Vol. 1, Issue 1, 1993, p. 7-31.

Search CrossRef
Dan A. Ralescu, Michio Sugeno Fuzzy integral representation. Fuzzy Sets and Systems, Vol. 84, 1996, p. 127-133.

Search CrossRef
Feng G., Cao S. G., Rees N. W. Stable adaptive control of fuzzy dynamic systems. Fuzzy Sets and Systems, Vol. 131, 2002, p. 217-224.

Search CrossRef
Zuperl U. F. Cus neural control strategy of constant cutting force system in end milling. Robotics and Computer Integrated Manufacturing, Vol. 27, Issue 3, 2011, p. 485-493.

Search CrossRef
Francisco de A. T. de Carvalho, Camilo P. Tenório Fuzzy K-means clustering algorithms for inter valued data based on adaptive quadratic distances. Fuzzy Sets and Systems, Vol. 161, Issue 23, 2010, p. 2978-2999.

Search CrossRef
Zhang Dong-B., Wang Yao-Nan, Huang Hui-Xian Fuzzy rough model based rough neural network modeling. Acta Automatica Sinica, Vol. 34, Issue 8, 2008, p. 1016-1023.

Search CrossRef

About this article

Received

19 April 2014

Accepted

25 April 2014

Published

15 May 2014

Keywords

flexible material path processing

deformation-compensated modeling

T-S fuzzy neural network

fuzzy clustering

Acknowledgements

This work is partially supported by National Natural Science Foundation of China (No. 51205069), Natural Science Foundation of Guangdong Province China (No. S2013010013288) and Combination project of Industry-university research of Foshan Shunde of Guangdong Province China (No. 2013CXY02). Thank you for all your help.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.