Experimental study of mechanical property for prestressed rubber bearing

Zou, Lihua; Li, Liangfeng; Zhang, Chao; Zhang, Wei; Xu, Zhixu

Journal of Vibroengineering

Browse Journal

Submit article

Published: 30 September 2014

Check for updates

Experimental study of mechanical property for prestressed rubber bearing

Lihua Zou¹

Liangfeng Li²

Chao Zhang³

Wei Zhang⁴

Zhixu Xu⁵

^{1, 3, 4, 5}School of Civil Engineering, Fuzhou University, Fuzhou 350108, China

²Fujian Academy of Building Research, Fuzhou 350001, China

Corresponding Author:

Chao Zhang

Cite the article Download PDF

Downloads 1149

Abstract

To overcome the shortages of existing Rubber Bearings (RBs), an innovative type of isolator, named as Prestressed Rubber Bearing (PRB), is presented in this paper. Base on conventional laminated Rubber Bearing (RB), PRB is developed by increasing the thickness of rubber layers, setting vertical ducts and installing prestress tendons. Through the vertical and horizontal monotonic loading test, the vertical and horizontal stiffness of PRBs are investigated. The empirical formulas for stiffness are proposed. Moreover, the hysteresis behavior and the energy dissipation capacity of PRBs are studied by reversed cyclic loading test. The results show that PRBs not only have the horizontal isolating capacity as conventional RBs, but also have the capacity of horizontal displacement-limitation and improved capacity of energy dissipation.

1. Introduction

The Rubber Bearings (RBs) have been widely installed in isolated structures as effective isolating devices [1]. The conventional RB became a research hot point in earthquake engineering. Li Yang employed quadratic sum-squares error method to identify the conventional RB’s parameter [2]. Animesh Das developed fiber-reinforced elastomeric base isolators to reduce conventional RB’s cost [3]. Dimos C. Charmpis optimized the elevation of seismic isolator to minimize earthquake response of multi-storey buildings in earthquake [4]. Although conventional RBs have been used widely and investigated systematically, they have some disadvantages: i) The capacity of horizontal displacement limitation is inadequate. The earthquake may cause large horizontal displacement in the rubber bearings and result in reduction of effective bearing area, which may leads to overturning of RBs due to the large second order moment; ii) The tensile strength is inadequate. The internal tensile force is forbidden to take place in RBs according to current Chinese Code. However, it is difficult to avoid in some situations such as the bearings installed in the bottom of high rise buildings; iii) The vertical isolating capacity is inadequate. Many earthquake disasters have shown that lots of non-structural damages are due to vertical vibration [6]. The vertical isolation devices will be helpful to reduce the lost in disasters.

To overcome the disadvantages of conventional RBs, several studies have been conducted. Kang et al. proposed fiber reinforced elastomeric isolator which used the carbon fiber and the glass fiber instead of steel plate to improve the vertical isolating capacity of RB [8]. Ismail [9, 10] introduced a new seismic system, named roll-n-cage isolator (RNC). The main bearing mechanism of the RNC is a hollow elastomeric cylinder of a designed thickness around a rolling body. The device incorporates isolation, energy dissipation, and inherent gravity-based restoring force mechanism in a single unit. Nagarajaiah S. et al. [11] proposed a Teflon-disc sliding bearing with built-in uplift restraint devices. Amarnath K. [7] suggested an uplift prevention mechanism which uses prestress to develop sufficient compressive force on the isolator. Roussis P. C. et al. [12] introduced a new XY-FP isolator, which possessed properties as uplift restraint, decoupling of the bi-directional motion along two orthogonal directions, and capability of providing independent stiffness and energy dissipation along the principal horizontal directions of the bearings. Ramallo J. C. et al. [13] introduced “Smart” base isolation system, which was composed of conventional low-damping elastomeric bearings and “smart” controllable (semi-active), to achieve notable decreases in base drifts. Zhang Yongshan [14] and Wei Liushun [15] proposed a new 3-dimensional isolation device, in which the vertical isolation capacity was developed by employing semi-active controlled hydro-cylinder that was parallel connected with vertical spring. However, among these studies, some devices were too complicated to be applied in engineering practice; some were proposed to overcome only one of the conventional RBs’ shortcomings. There is no device that can fully overcome all the disadvantages of conventional RBs.

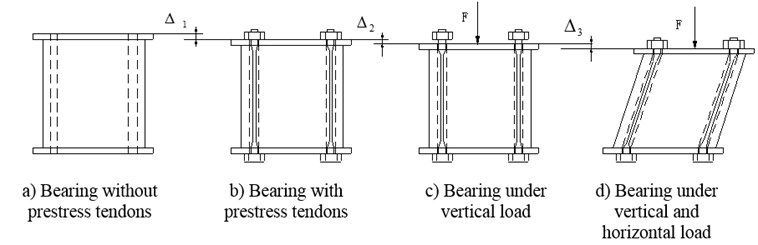
In this paper, an innovative type of rubber bearing, named as Prestressed Rubber Bearing (PRB) [Chinese patent number: ZL201020181364.1] is proposed. As shown in Fig. 1, PRB is developed based on conventional RB. The thickness of rubber layers are increased appropriately to improve the capacity of vertical isolation. Several vertical ducts are set and prestress tendons are installed. Fig. 2 shows the working mechanism of PRB. By applying prestress force, the vertical deformation of bearing takes place before the superstructure is constructed. When superstructure is finished, the prestress tendons are then relaxed. Hence the uneven vertical deformation which is caused by the small vertical stiffness of bearings can be eliminated. The relaxed tendons permit the bearing to deform horizontally in certain displacement range.

Fig. 1Structure of PRB

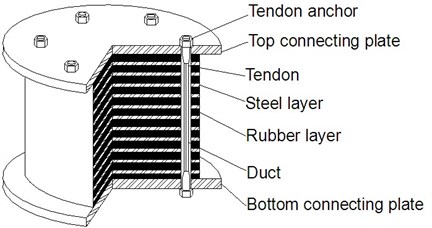
The proposed PRB has the following advantages: i) Due to the existence of prestress tendons, PRB has good capacity of both horizontal displacement limitation and uplift resistance; ii) Because most vertical deformation of bearings take place before applying the vertical load of superstructure, the vertical deformation due to dead load during construction period can be obviously reduced. So the uneven settlement can be eliminated in advance; iii) Since the thickness of rubber layers increase, the capacity of vertical isolation can be improved. Moreover, due to the capacity of horizontal displacement limitation, the effective area of bearing can be guaranteed in earthquake.

To investigate the working mechanism of PRBs, the vertical and horizontal monotonic loading test are conducted. Based on the experimental results, the empirical formulas for vertical and horizontal stiffness are derived. After that, the reversed cyclic loading tests of PRB are carried out. The energy dissipation capacity is discussed.

Fig. 2Working mechanism of PRB

2. The vertical monotonic loading test

The vertical stiffness is one of the important mechanical properties for rubber bearings. Because the rubber layers in proposed PRB are thicker than conventional RB and several ducts are set in the cross section, the formula of vertical stiffness for conventional RB may not be applicable for PRB. The vertical monotonic loading tests of PRB specimens without prestress tendons are conducted to investigate vertical stiffness of PRB.

2.1. Specimen and experimental set-up

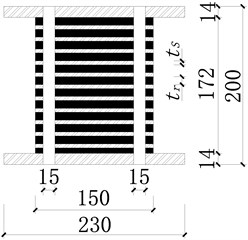
Specimens: There are 6 groups PRBs with 3 specimens in each group are tested. The height of bearings $H$ are 200 mm, the thickness of connecting plates are 14 mm, the diameter of effective cross sections $D$ are 150 mm, and the diameter of ducts $d_{0}$ are 15 mm. The dimensions of specimens are show in Fig. 3 and the detailed parameters are listed in Table 1, in which $t_{r}$ is the thickness of rubber layers; $t_{s}$ is the thickness of steel layers; $S_{1}$ , $S_{2}$ are the first and second shape coefficient, which can express as:

1

S_{1} = \frac{d^{2} - m {d_{0}}^{2}}{4 t_{r} (d + m d_{0})},

2

S_{2} = \frac{d}{n t_{r}},

where, $m$ is the number of the ducts, $n$ is the number of rubber layers.

Fig. 3Dimension of PRB specimens

Set-up: The experiments are conducted by computer controlled compression testing machine with maximum load of 300 kN and maximum stroke of 500 mm. The experimental set-up is shown in Fig. 4.

Fig. 4Experimental set-up of vertical loading test

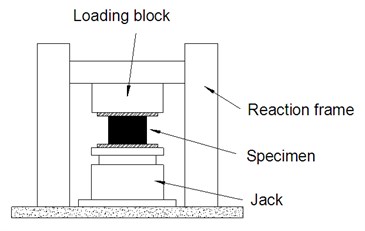
Table 1Parameters of specimens

No.	$t_{r}$ / mm	$t_{s}$ / mm	$S_{1}$	$S_{2}$
PRB-1	10.6	1	2.08	0.94
PRB-2	9.24	1	2.38	0.95
PRB-3	7.7	1	2.86	0.97
PRB-4	9.6	2	2.29	1.04
PRB-5	8.2	2	2.67	1.07
PRB-6	6.7	2	3.29	1.12

2.2. Experiment result

The vertical monotonic loading test is conducted by displacement control with the loading step of 1 mm. Fig. 5 shows the relationship of vertical load and displacement.

Fig. 5Relationship of vertical load and displacement

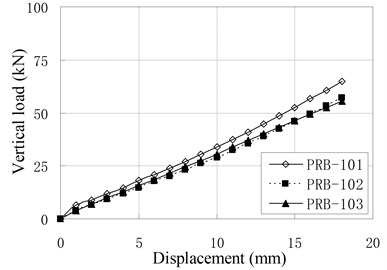
a) PRB-1

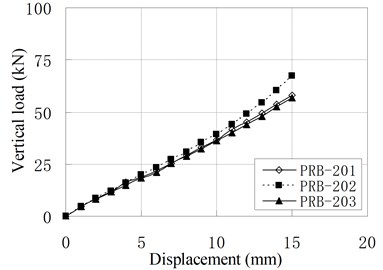
b) PRB-2

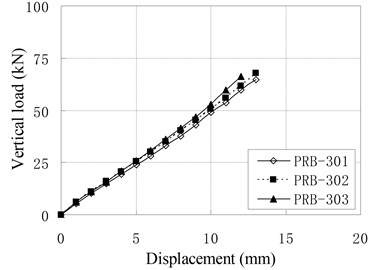
c) PRB-3

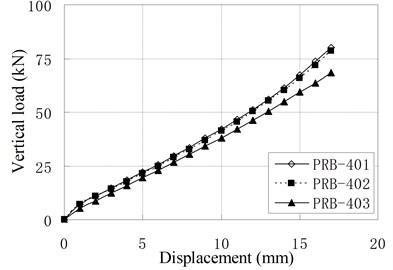
d) PRB-4

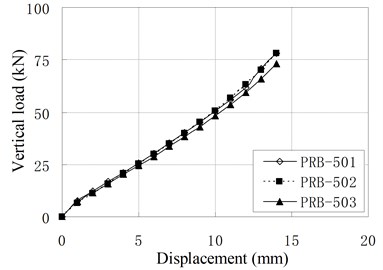
e) PRB-5

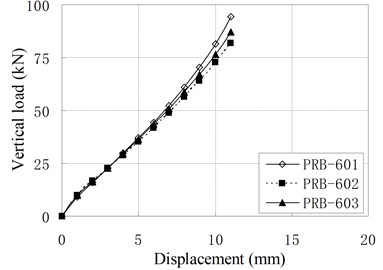
f) PRB-6

It can be seen that the relationships of vertical load and displacement are linear. The value of vertical stiffness is in the range of 3 kN/mm to 8 kN/mm, which is much smaller than conventional RBs of similar dimension. The small vertical stiffness can improve the vertical isolation capacity of bearing. According to Chinese Code, the vertical stiffness for conventional RBs are expressed as [16]:

3

K_{V} = \frac{E_{c b} A}{n t_{r}},

where, $A$ is the effective bearing area of RB; $E_{c b}$ is the compression modulus of RB, $E_{c b} = E_{c} E_{b} / (E_{c} + E_{b})$ ; $E_{b}$ is the constrained elastic modulus of rubber; $E_{c}$ is the corrected elastic modulus of rubber, $E_{c} = E (1 + 2 k S_{12})$ ; $E$ is the elastic modulus of rubber; $k$ is the correcting coefficient according to rubber’s hardness.

Fig. 6Comparison of vertical load-displacement curves corresponding to test result and Chinese Code

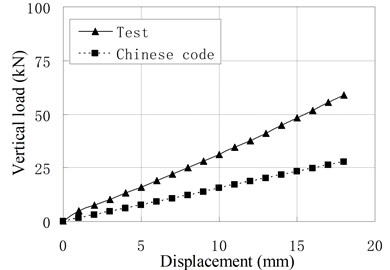
a) PRB-1

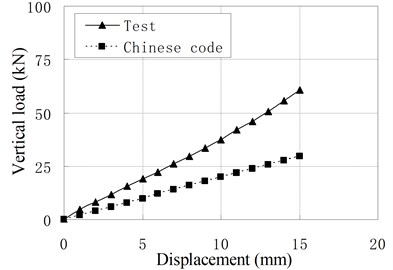
b) PRB-2

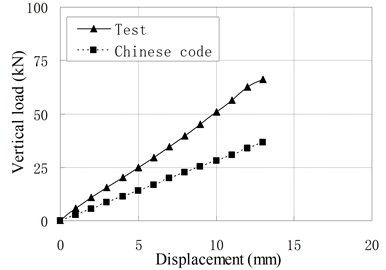
c) PRB-3

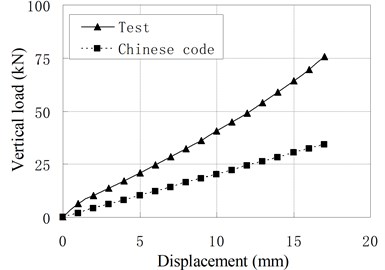
d) PRB-4

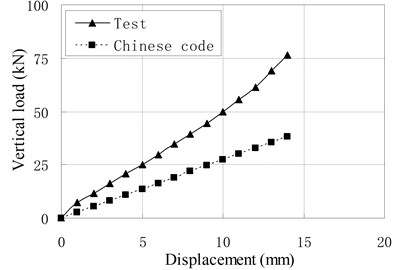
e) PRB-5

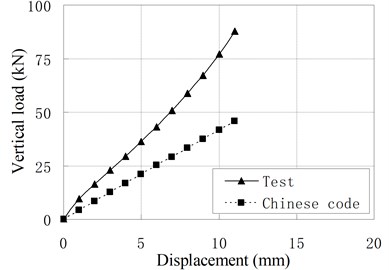
f) PRB-6

Fig. 6 compares vertical load-displacement curves calculated by Eq. (3) with the test results. It shows that the vertical stiffness from test results is much larger than stiffness from code’s formula. The maximum discrepancy is about 1.09 times of the latter. The main reason is that the steel plate’s lateral constraint to rubber layer is changed due to the increase of rubber layers’ thickness and the existing of vertical ducts. The code’s formula underestimates greatly the constraint effect of steel layer on the rubber layers. For PRB, the Eq. (3) can be modified as follows:

4

K_{V} = η \frac{E_{c b} A}{n t_{r}},

where, $η$ is a modifying coefficient of vertical stiffness. By linear regression analysis of test results, the modifying coefficient $η$ can be obtained as:

5

η = - 0.23 S_{1} + 2.56 .

Due to the limitation that only 18 samples are used in regression analysis and only the first shape factor is considered, the formula can only be applied to the PRBs with similar dimension.

3. The horizontal monotonic loading test

To investigate the horizontal stiffness for PRB, the horizontal monotonic loading tests are carried out. The empirical formulas for horizontal stiffness of PRB are then proposed.

3.1. Experimental set-up

Set-up: The experimental set-up and loading system are shown in Fig. 7. The bottom connecting plate is fixed in base and the top connecting plate is fastened to a loading block whose rotation deformation is constrained. The vertical load is generated by a pressure-controlled hydraulic jack, and the horizontal load is generated by a servo-controlled hydraulic actuator with maximum load of 250 kN and maximum stock of ±250 mm.

Fig. 7Experimental set-up of horizontal monotonic loading

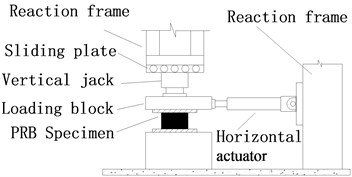
a)

b)

The displacement control method with step of 10 mm is employed in the horizontal loading. Both loading procedure and horizontal displacement measurement are controlled by computer. The specimens which used in the vertical loading test are still used in horizontal loading test.

3.2. Experiment procedure and result

According to the condition of the vertical load, the monotonic horizontal loading tests can be classified as pure shear test and compression shear test.

3.2.1. Pure shear test

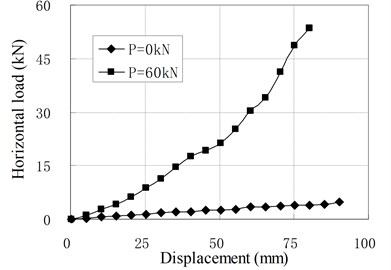
When the vertical load equals to zero, the horizontal loading tests are named as pure shear test. To investigate the influence of prestress tendons, both kinds of bearings with the installation of tendons and without the installation of tendons are tested. The relationships of horizontal resisting force and displacement are shown in Fig. 8, where $P$ is the value of prestress force and the value of zero represents no installation of prestress tendons.

Fig. 8Relationship of horizontal load and displacement for pure shear

a) PRB-1

b) PRB-2

c) PRB-3

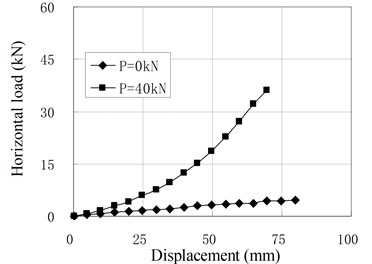
d) PRB-4

When there is no prestress tendon, the horizontal stiffness of the isolators is small and close to a constant, that is similar to conventional RBs. When there is prestress force, the force-displacement curves are not straight lines any longer. Although the initial stiffness of PRB is small, the stiffness increases gradually as increase of the displacement. The main reason is that the prestress tendons can be considered as non-elongated tendons because their elastic modules are much larger than the rubber. Due to the compatibility of deformation, the horizontal deformation of the bearing will lead to vertical deformation of rubber layers. In the initial stage of the horizontal deformation, the prestress tendons are perpendicular to the horizontal direction. The vertical deformation of rubber layers caused by horizontal deformation is small. Therefore, the initial stiffness of PRB is small and close to the value of the conventional RB with same dimensional parameters. In the stage of large horizontal deformation, the angles between the tendons and horizontal direction because smaller. The vertical deformation caused by horizontal deformation is increased. To compress the rubber layers, the tensile force in tendons increase correspondingly, which increases the horizontal resisting force of PRBs. Therefore, the horizontal stiffness of PRB increases as the increase of horizontal displacement.

3.2.2. Compression shear test

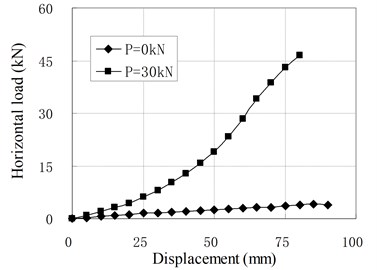
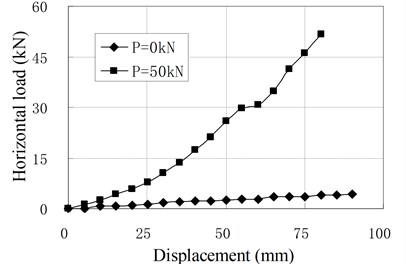
When the vertical load is larger than zero, the horizontal loading tests are called compression shear test. The relationships of horizontal load and displacement under different vertical load are shown in Fig. 9, in which $F$ is the value of vertical load; $P$ is the prestress force.

Fig. 9Relationship of horizontal load and displacement for compression-shear test

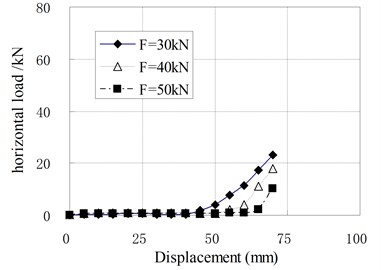
a) PRB-1 with $P =$ 30 kN

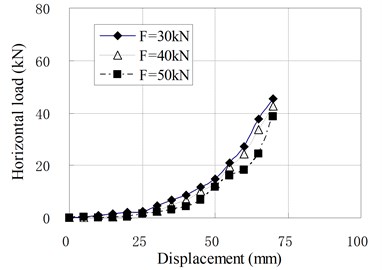
b) PRB-2 with $P =$ 30 kN

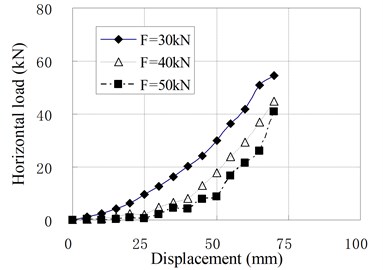
c) PRB-3 with $P =$ 60 kN

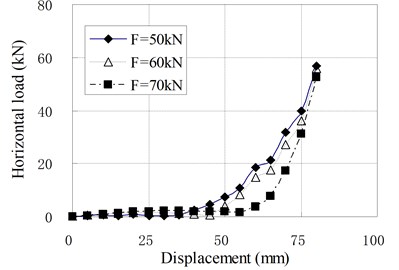
d) PRB-4 with $P =$ 40 kN

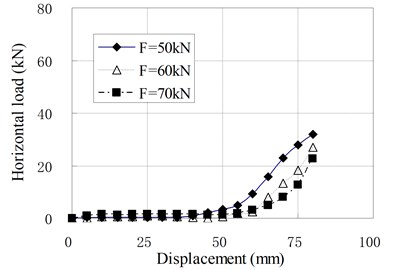
e) PRB-5 with $P =$ 40 kN

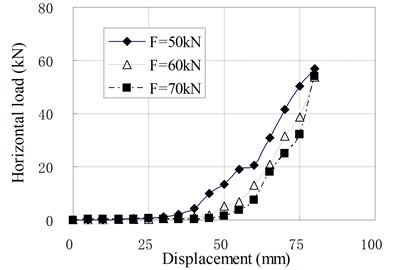
f) PRB-6 with $P =$ 60 kN

The mechanical properties of PRB in the compression shear condition are similar to that in pure shear condition with prestess force. The horizontal stiffness is small and constant at the initial stage of horizontal deformation. When the horizontal displacement exceeds a certain value, the horizontal stiffness begins to increase gradually with increase of the horizontal displacement. There is an obvious inflection point between linear and nonlinear segments of load-displacement curves which is different from curves under the pure shear condition. It can be seen that the position of inflection point is determined by vertical load. The inflection point will appear in larger displacement when a greater vertical load is applied. The reason is that the prestress tendons relax under the vertical load. The relaxed tendons permit the bearing to deform freely in a certain range of displacement. This displacement range increases as the vertical load increases. When the horizontal displacement of top plate reaches the inflection point, the relaxed tendons are tensed again. In this state, the tendons begin to compress the bearing. Because the horizontal force components of tendons participate in the horizontal force balance of bearing, the horizontal stiffness suddenly increases.

3.3. Horizontal stiffness of PRB

According to the horizontal monotonic loading tests, it can be seen that the PRB is a kind of bearings with variable stiffness, which is different from conventional RBs. Therefore the code formula for the stiffness of conventional rubber bearing is not suitable for PRB. The horizontal stiffness for PRB without prestress tendons and with prestress tendons are respectively developed in this paper.

3.3.1. Horizontal stiffness of PRB without tendons

The horizontal stiffness formula for conventional rubber bearing is [16]:

6

K_{h} = \frac{G A}{n t_{r}},

where, $G$ is the shear modulus of rubber. Because of the increase of rubber layers’ thickness, not only the shear deformation but also the flexural deformation takes place under horizontal loading. Hence, the lateral stiffness is smaller than the code formula in which only shear deformation is under consideration. A modified formula by regression analysis is proposed in this paper. Since the flexural deformation is affected by height-diameter ratio of rubber bearings, the second shape coefficient is selected as the variable. The horizontal stiffness of PRB without prestressing force can be expressed as:

7

K_{h} = φ \frac{G A}{n t_{r}},

8

φ = 0.71 S_{2} + 0.16 .

For the PRB with prestressing force, because the horizontal component of tendon’s tension contributes to the horizontal resistance of PRB, Eq. (7) cannot be applied in this situation. The PRB’s horizontal rigidity is changed with the deformation. Base on the compatibility of deformation and the geometrical relationship, the horizontal stiffness formula can be written in two sets of formulas according to the condition of vertical load.

For pure shearing working condition ( $F =$ 0), the horizontal stiffness is expressed as:

9

K_{p h} = K_{h} + α K_{v} \frac{Δ v}{H' - Δ v},

where, $K_{p h}$ is horizontal stiffness for pure shear working condition; $K_{h}$ is the horizontal stiffness without prestressing force which can be computed from Eq. (7); $K_{v}$ is the vertical stiffness of PRB; $H'$ is the height of PRB after prestressing, $H' = H - P / K_{h}$ ; $H$ is the total height of PRB before prestressing; P is the value of prestress force; $Δ v$ is the vertical displacement of top connecting plate, which is calculated as $Δ v = H' - \sqrt{{H'}^{2} - Δ h^{2}}$ ; $Δ h$ is the horizontal displacement of top connecting plate. It can be seen that the value of horizontal stiffness is a function of deformation $Δ h$ . The derivation of Eq. (9) is based on the assumption that only shear deformations are developed and the tendons maintain as straight lines. However, the flexural deformations also take place. The modifying factor $α$ which accounts for this discrepancy between theory and reality is obtained by regression analysis from experimental result and expressed as:

10

α = - 3.21 S_{2} + 4.90 .

For compression shearing working condition ( $F \neq$ 0), the horizontal stiffness is written as:

11

K_{p h}^{'} = K_{h} + β (P + K_{V} Δ v - F_{}) / (H^{'} - Δ v), K_{v} Δ v > F_{},

K_{p h}^{'} = K_{h}, P + K_{v} Δ v - F_{} \leq 0,

where, $β$ is the modifying factor and obtained as:

12

β = - 1.56 S_{2} + 2.74 .

Fig. 10Relationship of horizontal load and displacement corresponding to test and proposed formula

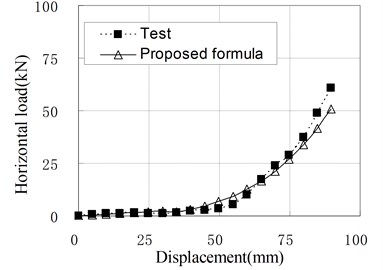
a) PRB-1 with $P =$ 50 kN, $F =$ 60 kN

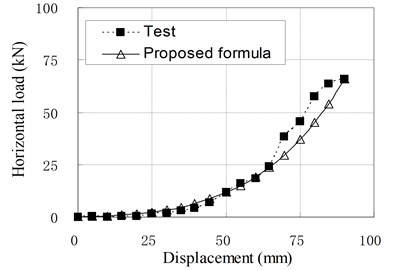
b) PRB-2with $P =$ 50 kN, $F =$ 50 kN

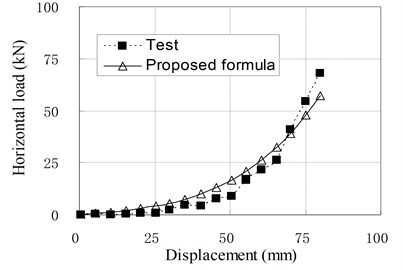
c) PRB-3 with $P =$ 60 kN, $F =$ 50 kN

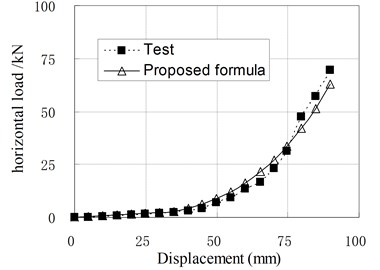
d) PRB-4 with $P =$ 60 kN, $F =$ 70 kN

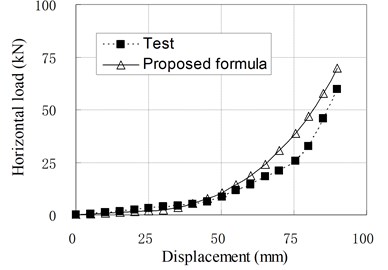
e) PRB-5 with $P =$ 40 kN, $F =$ 50 kN

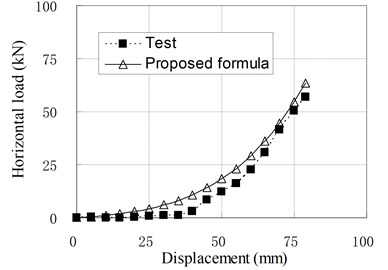
f) PRB-6 with $P =$ 40 kN, $F =$ 30 kN

Since the isolators generally work in compression shear condition, the Eq. (11) is used in common situations. To check the applicability of above formula, the load-displacement curves calculated by Eq. (11) are compared with some test results which are not included in the regression samples, and shown in Fig. 10. It can be seen that they agree well with each other. Therefore, it can be thought that the proposed formulas for horizontal stiffness of PRB are appropriate. However, due to the small number of regression analysis samples, the modifying factors used in the formulas are only applicable to PRB similar to experimental specimens.

4. Reversed cyclic loading test

The reversed cyclic loading test is one of experimental methods to exam the hysteretic property of isolator [17, 18], and it is also adopted in this research. The purpose of reversed cyclic loading test is to investigate the relationship between restoring-force and displacement of PRBs. And the property of viscous damping cannot be investigated.

4.1. Experimental set-up and loading arrangement

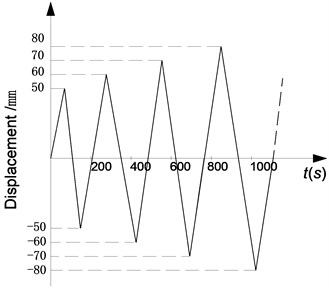
The experimental set-up used in the horizontal monotonic loading test is also used in the reversed cyclic loading tests. A horizontal loading displacement, which has a constant rate of loading and an increased magnitude for every cycle from 50, 60, 70 to 80 mm, is applied to the specimens. Because the loading rate has little effect on the experiment results when the loading rate is very small, the triangle waves as shown in Fig. 11 are employed for the reason of easily operation of actuator. The force and the displacement are measured by the sensor of the actuator and the sampling frequency is 1 Hz.

Fig. 11Cyclic loading arrangement

4.2. Experiment result

Fig. 12 shows hysteresis behavior of PRBs in the reversed cyclic loading. Three groups of specimens (PRB-1, PRB-2, PRB-4) are selected for the tests. The specimens in each group are subjected to same prestressing force but different vertical loads to investigate the influence of vertical loads.

The backbone of the hysteresis curve is similar to the force-displacement relationship of monotonic loading test. The backbone is small and constant at the initial stage, and increase gradually with increase of the horizontal displacement. In the hysteresis curve, the reloading paths almost cover the previous loading paths, and no strength degradation phenomenon is observed. The unloading stiffness is larger than the loading stiffness. When the horizontal force is reduced to near zero value, the unloading stiffness decreases rapidly and the unloading paths become almost parallel to the horizontal axis.

When the displacement is small, the hysteresis curve of PRB is slender and similar to the shape of the conventional RB, in which only small amount of energy is dissipated. The area closed by hysteresis loops increase gradually as increase of loading displacement. So the capacity of energy dissipation increases in the large deformation stage.

Comparing the two curves of same PRB under different vertical loading, it can be found that the areas closed by hysteresis loops are affected by the value of vertical load. The smaller the vertical load is, the more energy the PRBs dissipate. The main reason is that the load-displacement curve of PRB is approximately linear in the small deformation stage. Little energy can be dissipated during the reversed deformation. When the displacement load becomes large, the PRB deforms in the nonlinear stage. Due to the existing of friction, the unloading stiffness is larger than the loading stiffness. So the areas closed by the hysteresis loops become large, and dissipated energy increases. Moreover, when vertical load is reduced, the relaxed length of tendon decreases and the nonlinear deformation will happen in early stage. Therefore, more energy is dissipated under the small vertical load. Compared with conventional RBs, the PRB has better energy dissipation capacity under the same working conditions.

Fig. 12Hysteretic behaviors

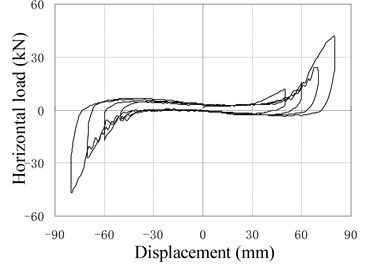
a) PRB-1 with $P =$ 30 kN, $F =$ 30 kN

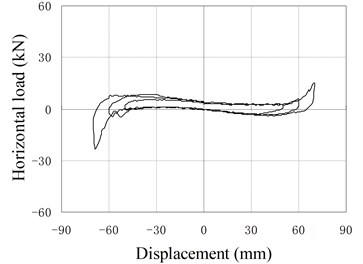
b) PRB-1 with $P =$ 30 kN, $F =$ 40 kN

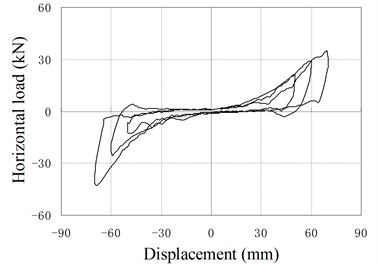
c) PRB-2 with $P =$ 50 kN, $F =$ 30 kN

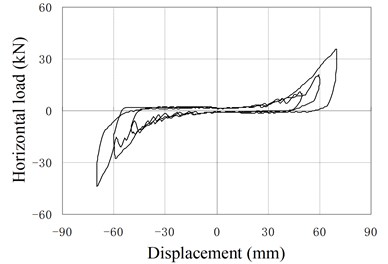
d) PRB-2 with $P =$ 50 kN, $F =$ 40 kN

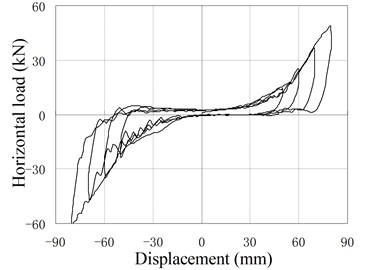
e) PRB-4 with $P =$ 40 kN, $F =$ 30 kN

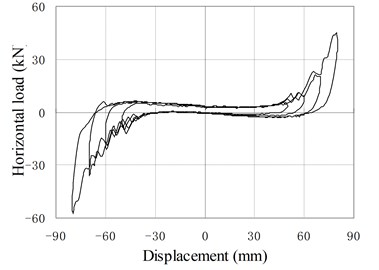
f) PRB-4 with $P =$ 40 kN, $F =$ 50 kN

5. Conclusions

1) PRBs can satisfy the general requirements of seismic isolators and overcome the disadvantages of conventional RBs. Moreover, PRBs also have good capacities of uplift resistance and horizontal displacement limitation.

2) The horizontal stiffness of PRBs is variable. Because the working mechanism of PRBs is different from conventional RBs, the formulas for the stiffness of ordinary RBs can not be applied for PRBs. The mechanic properties of PRBs are tested and modified formulas for the stiffness of PRBs are proposed.

3) Compared with conventional RBs, the PRBs have better energy dissipation capacity under the same conditions.

References

Skinner R. I.,Robinson W. H., Mcverry G. H. An Introduction to Seismic Isolation. John Wiley&Sons. 1993.

Search CrossRef
Li Y., Zhou L. Experimental study on parameter identification of rubber-bearings based on quadratic sum-squares error. Journal of Vibroengineering, Vol. 15, Issue 1, 2013, p. 204-210.

Search CrossRef
Animesh D., Anjan D., Sajal K. D. Performance of fiber-reinforced elastomeric base isolators under cyclic excitation. Structural Control and Health Monitoring, 2014.

Search CrossRef
Charmpis D. C., Komodromos P., Phocas M. C. Optimized earthquake response of multi-storey buildings with seismic isolation at various elevations. Earthquake Engineering & Structural Dynamics, Vol. 41, Issue 15, 2012, p. 2289-2310.

Search CrossRef
Zhou X. Y., Ma D. H., Zeng D. M., Han M. A formula for horizontal stiffness of composited isolators. China Civil Engineering Journal, Vol. 33, Issue 6, 2000, p. 38-44.

Search CrossRef
Gulerce Z., Erduran E., Kunnath S. K., Abrahamson N. A. Seismic demand models for probabilistic risk analysis of near fault vertical ground motion effects on ordinary highway bridges. Earthquake Engineering and Structural Dynamics, Vol. 41, Issue 2, 2012, p. 159-175.

Search CrossRef
Amarnath K., Michael C. C. Testing and modeling of pre-stressed isolators. Journal of Structural Engineering, 2005, p. 857-866.

Search CrossRef
Kang B. S., Kang G. J., Moon B. Y. Hole and lead plug effect on fiber reinforced elastomeric isolator for seismic isolation. Journal of Materials Processing Technology, Vol. 140, 2003, p. 592-597.

Search CrossRef
Ismail M., Rodellar J., Ikhouane F. An innovative isolation device for aseismic design. Engineering Structures, Vol. 32, 2009, p. 345-356.

Search CrossRef
Ismail1 M., Rodellar J., Pozo F. An isolation device for near-fault ground motions. Structural Control and Health Monitoring, Vol. 21, 2014, p. 249-268.

Search CrossRef
Nagarajaiah S., Reinhorn A. M., Constantinou M. C. Experimental study of sliding isolated structures with uplift restraint. Journal of Structural Engineering, Vol. 118, 1992, p. 1666-1682.

Search CrossRef
Roussis P. C., Constantinou M. C. Experimental and analytical studies of structures seismically isolated with an uplift-restraining friction pendulum system. Earthquake Engineering and Structural Dynamics, Vol. 35, 2006, p. 595-611.

Search CrossRef
Ramallo J. C., Johnson E. A., Spencer Jr. B. F. “Smart” base isolation systems. Journal of Engineering Mechanics, Vol. 128, 2002. p. 1088-1100.

Search CrossRef
Zhang Y. S., Yan X. Y., Wang H. D., Wei L. S., Zhao G. F. Experimental study on mechanical properties of three-dimensional base isolation and overturn resistance device. Engineering Mechanics, Vol. 26, Issue 1, 2009, p. 121-126, (in Chinese).

Search CrossRef
Wei L. S., Zhou F. L., et al. Application of three-dimensional seismic and vibration isolator to building and site test. Journal of Earthquake Engineering and Engineering Vibration, Vol. 27, Issue 3, 2007, p. 121-125, (in Chinese).

Search CrossRef
Zhou F. L. Vibration Reduction and Control of Structure Engineering. Beijing, Seismic Press, 1997, (in Chinese).

Search CrossRef
Naghshineh A. K., Akyüz U., Caner A. Comparison of fundamental properties of new types of fiber-mesh reinforced seismic isolators with conventional isolators. Earthquake Engineering and Structural Dynamics, Vol. 43, 2014, p. 301-316.

Search CrossRef
Lu L. Y., Lee T. Y., Yeh S. W. Theory and experimental study for sliding isolators with variable curvature. Earthquake Engineering and Structural Dynamics, Vol. 40, 2011, p. 1609-1627.

Search CrossRef

About this article

Received

06 March 2014

Accepted

22 August 2014

Published

30 September 2014

Keywords

isolator

prestress tendon

horizontal displacement limitation

energy dissipation

Acknowledgements

This work was financially supported by Chinese Housing and Urban-Rural Construction Ministry under Grant No. 2009-R4-8.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.