Research on transverse parametric vibration and fault diagnosis of multi-rope hoisting catenaries

2.1. Transverse vibration model of catenary

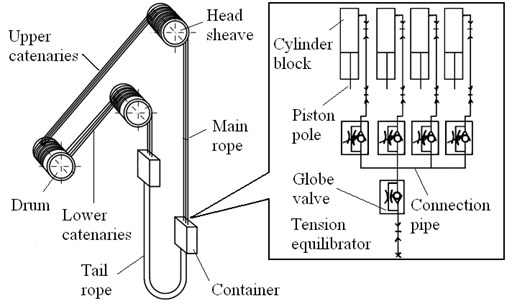
We consider that the gravity difference of catenary can be neglected compared to its large tension. The inclined catenary shown in Fig. 1 can be modeled as a horizontal axially moving string in Fig. 2.

In this diagram $L$represents the length of the string. $\rho$, $c\left(t\right)$ are the line density and the axial moving speed. $y\left(x,t\right)$ is the transverse displacement of the string at position $x$ at time $t$. $e_1\left(t\right)$, $e_2\left(t\right)$ are the axial deflection displacements of the drum or head sheave grooves along the $y$ axis.

Fig. 2Axially moving string model with boundary excitations

The transverse vibration of catenary in the $xy$ plane is governed by:

where $P\left(t\right)$ is the string tension at time $t$. Under the condition of imbalanced tensions, the imbalance coefficient $b_i$ is introduced to take that fact into account. $k$ is the number of the catenaries. $P_k\left(t\right)$ and $P_A\left(t\right)$ are the tension of catenary $k$ and the mean balanced tension of all catenaries. The $P_k\left(t\right)$ and $P_A\left(t\right)$ are given by Eq. (2) and Eq. (3):

where $\sum m\left(t\right)$ is the whole equivalent mass of the hoisting equipments along the catenary side [1]. $m_{er}$ is the equivalent mass of the head sheave. $n_1$ denotes the number of the main ropes. $g$ is the gravitational acceleration. The whole equivalent mass is given by:

where ${\rho }_w\mathrm{}$is the line density and $n_2$ is the number of the tail ropes. $h$ is the hoisting height. $l\left(t\right)$ denotes the time-varying length of main ropes during hoisting process.$\mathrm{}{m}_m$, $m_z$ and $m_q$ are the masses of the hoisting load, the container and the attached parts respectively. The attached parts include the tension equilibrator.

2.2. Boundary harmonic excitations

As shown in Fig. 1 and Fig. 2, the axial deflection displacements of the winder drum or the head sheave grooves generates the transverse displacement excitations to both ends of moving catenary. These inhomogeneous boundary excitations are given by Eq. (5):

where $e_1\left(t\right)$, $e_2\left(t\right)$ are the deflection displacements and can be simulated and give by:

where $c\left(t\right)$ is the axial speed and $R$ is the rotation radius of the drum or the head sheave grooves. The dependent $n$-order displacement amplitudes $a_{1n}$, $a_{2n}$ and phases ${\phi }_{1n}$, ${\phi }_{2n}$ are subjected to equipment faults or deformations.

The vibration function with inhomogeneous boundary conditions can be further decomposed by Eq. (7):

$U\left(x,t\right)$ refers to the function with homogeneous boundary conditions given by:

$W\left(x,t\right)$ is the function with inhomogeneous boundary conditions given by:

The excitations are transferred from the boundary to the domain without losing the generality by Eq. (10):

2.3. Vibration equations solution

Galerkin’s method is used to discretize the governing partial differential Eq. (1). The assumed form of the displacement response of the moving string homogeneous function is:

where $N$ is the number of included modes. $q_j\left(t\right)$ are the generalized coordinates relevant to time $t$. $X_j\left(x\right)$ are the trial functions and defined by Eq. (12):

Substituting Eq. (6), Eq. (7), Eq. (11) and Eq. (12) into Eq. (1), then multiplying the equation by $X_i\left(x\right)$$(i=\mathrm{}$1, 2,…,$N)$, integrating it from $x=0$ to $L$, and using the boundary condition yields the discretized equations as:

where $\mathbf{q}{\left(t\right)=\left(q_1{q}_2\dots q_j\right)}^T$ is the vector of generalized coordinates. The mass, stiffness, damping and force matrices are:

where ${\delta }_{ij}$ is the Kronecker delta. Damping and stiffness matrices $\mathbf{C}$, $\mathbf{K}$ in the discretized equation Eq. (13) are subjected to axial velocity $c\left(t\right)$ of catenaries, where the generalized force matrix is decided by axial velocity $c\left(t\right)$, and deflection displacements of the winder drum and head sheaves grooves $e_1\left(t\right)$, $e_2\left(t\right)$.

Eq. (13) is the coupling coefficient second order ordinary differential equations. The numerical method to solve it is to discretize the movement cycle into time internals, where during each time internal the matrices in Eq. (13) remain constant. The Newmark-beta method was applied into the numerically evaluation of the Eq. (13), with $\beta =$0.25.

3.1. Transverse vibrations displacements test of catenaries

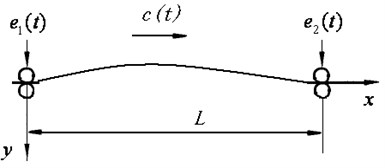
The non-contact video gauge system was used to measure the transverse vibrations displacements of catenaries. The processed images were shown in Fig. 3. The left part of the figure indicates the catenaries’ distribution with marked numbers 1# to 4# and the measurement plane with grids. The right part shows two frames of measured videos.

Fig. 3Non-contact video gauge processed images

The plane appearing as a red grid overlaid in the image in Fig. 3 is the coordinates frame to define the measuring scale of vibration displacements. The $Y$-axis points to the longitudinal direction of catenaries while $X$ axis points to the lateral. The scaling factor to the pixel measurements is calculated by two points over a known distance from 1# to 4# catenary in the image, which appears from origin of plane to the point with “o” mark along the $Y$ axis. With these coordinates for the geometry measurement, the catenaries transverse vibration displacements were recorded and analyzed.

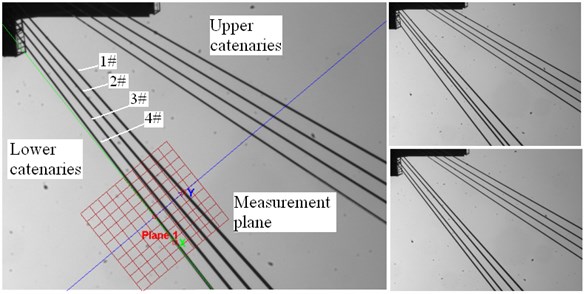
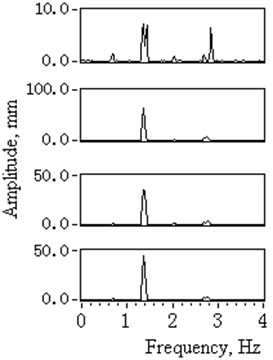
The vibration displacements of four lower catenaries with $x=L/2$ were shown in Fig. 4 and the statistic results were listed in Table 1. Fig. 4(a) shows the measured 42 seconds time domain curves numbered by 1# to 4# with constant high hoisting speed. Fig. 4(b) shows the corresponding zoomed amplitude spectrum with the 0.024 Hz frequency resolution.

The vibration spectrum of 2#, 3# and 4# catenaries under empty container circumstances had the same characteristic of resonance. The main frequency ranged from 1.35 Hz to 1.38 Hz and was close to the 1.34 Hz, which is the 2nd harmonic of the winder drum and head sheaves rotation frequency. The spectrum of 1# catenary had main frequencies such as 1.43 Hz, 1.35 Hz and 2.85 Hz without any characteristic of resonance.

The displacement amplitudes of 1# to 4# catenaries under a fully loaded container circumstance were normal and significantly less than those under empty container circumstances. The amplitude spectrum shows the main vibration frequencies varying from 1.62 Hz to1.64 Hz. Under the fully loaded container circumstances, all four catenaries' vibrations showed no characteristic of resonance.

According to Eqs. (14)-(16), all four catenaries shared the same parameters and should have had the same natural frequencies. The measured vibration displacements had different amplitudes and frequencies. The accountable parameters leading to these conditions could be attributed to excitation amplitudes $a_{ij}$, phases ${\phi }_{ij}$, and imbalance catenaries tension $P\left(t\right)$. Further tests need to be conducted on the axial vibration displacements $e\left(t\right)$ of the winder drum and head sheaves grooves, along with the tension$P\left(t\right)$.

Fig. 4Time domain and spectrum diagram of lower catenaries transverse vibrations (1# to 4#)

a) Time domain signal

b) Amplitude spectrum

3.2. Deflection displacements test of the winder drum and head sheaves

Fig. 1 shows that each catenary has the same numbered separate head sheave, so the axial groove deflection displacement $e\left(t\right)$ was measured through the steel outer ring of the head sheave indicated in Fig. 5.

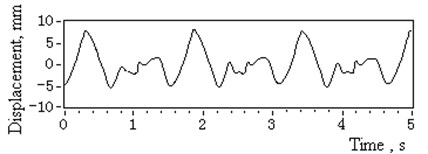
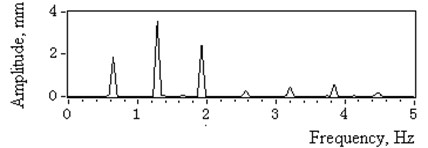
A bearing rod bolstered the CCD laser displacement sensor facing the outer ring. The catenaries shared the same drum so they had the same axial vibration displacement of the drum grooves. The statistical measurement results obtained are listed in Table 2. The measured time domain displacement and its amplitude spectrum of 3# head sheave are illustrated in Fig. 6. The rotation frequency of the head sheaves is 0.67 Hz.

Fig. 5Measurement schematic of head sheaves axial deflection displacement

Fig. 6Deflection displacement and amplitude spectrum of 3# head sheave

a) Time domain signal

b) Amplitude spectrum

See Table 2. Note that the deflection displacement amplitudes of 1# head sheave and the drum are within the normal range, while the others exceed the 2 mm limit and could be identified as a faulty condition. The amplitude of harmonic frequency 1.34 Hz referred as $a_{12}$ or $a_{22}$ in Eq. (6) was listed as the main boundary excitation of catenaries.

3.3. Catenaries tension test

The tension imbalance condition can be derived from the measurement of oil pressure of tension equilibrator. Fig. 7 presents the pressure-time cures of the container downward movements from shaft top to shaft bottom. The thick solid line represents measured tensions $P\left(t\right)$ of certain catenaries, while the thin dot line represents the normal cure of mean balanced tension $P_A\left(t\right)$ recorded before and validated by analytical calculation.

Fig. 7Oil pressure of tension equilibrator under the empty container circumstance

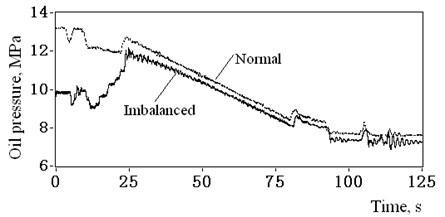
It could be concluded through the comparison of the two cures that the measured data indicated a serious imbalanced tension problem. Some catenary tensions $P\left(t\right)$ are far too low to average balanced tension $P_A\left(t\right)$ with the relative ratio varying from 75 % to 92 %, whereas the others were greater than the $P_A\left(t\right)$.

The tension measurement of each catenary could not be conducted due to practical technical problems. Observations indicated that the piston pole of 1# hydro-cylinder reached the top limit position of cylinder blocks, and, therefore, it had the greater tension. It was clear that the difference in catenaries’ tensions was induced by the malfunction of the tension equilibrator, while the relation of tension variation and vibration resonance still needs to be studied in this case.

4.1. Transverse vibrations displacements simulation

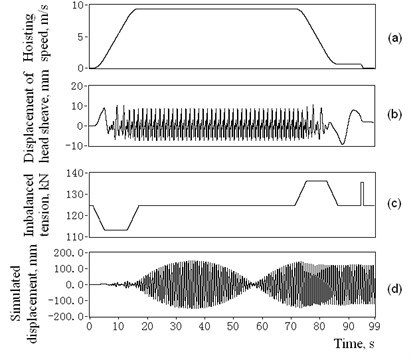
In order to validate the dynamic model of catenaries transverse vibrations in Eq. (1) and to determine the major factor leading to parametric vibration, the practical test data collected in Section 3.2 and Section 3.3 were synthesized into the simulation cures plotted in Fig. 8(a)-(c), which are the hoisting speed $c\left(t\right)$, the deflection displacements $e\left(t\right)$ of 4# head sheave groove, imbalanced tension $P_A\left(t\right)$ of 4# catenary with imbalance coefficient $b_4=$0.9 under the circumstance of empty container. The other parameters required in the simulation are provided in Table 3.

The 4# catenary displacement-time simulation response with $x=L/2$ and the included mode number $N=$16 was shown in Fig. 8(d), which shows a characteristic of resonance with its main frequency as 1.37 Hz. Taking the deflection displacements measured results into account and assuming the tension imbalance coefficients of catenaries 1# to 4# are 1.31, 0.89, 0.91, 0.90, the maximum simulation vibration amplitudes of 1# to 4# catenaries at $x=L/2$ are 17.5 mm, 155 mm, 102 mm and 147 mm. These amplitudes are close to the measured data in Table 1 and are characterized primarily by the same amplitude spectrum. The simulation validates the applicability and reliability of the model in Eq. (11), along with its numerical method.

Fig. 8Simulation of the excitation signals and the response vibration displacements of 4# catenary

4.2. Fault diagnosis

The simulation results in Section 4.1 showed that the transverse displacements of catenaries had different maximum amplitudes with different tension imbalance coefficients. They were constrained by the boundary excitation results from deflection displacements of the head sheaves and drum grooves. The effects of tension and boundary excitation on large vibrations need to be investigated to identify the fault sources.

4.2.1. Tension variation and vibration simulation

Due to the dynamic tension variation of certain catenary, the imbalance coefficient can vary within a given range. Take 4# catenary as the example to illustrate the effect of different imbalance coefficients on its vibration amplitudes. When $b_4$ varies from 0.8 to 1.2, with its boundary excitation of deflection displacements shown in Fig. 8, the 3D surface graph of catenaries vibration amplitudes of descending movement under empty load condition is presented in Fig. 9(a). Also the transverse natural frequencies of 4# catenary during constant speed period are presented in Fig. 9(b), where the dotted lines indicate the 1st to 5th boundary harmonic excitation frequencies. The solid lines indicate the first two natural frequencies of 4# catenary.

Note that when $b_4=$0.86, the first two natural frequencies 1.334 Hz and 2.668 Hz coincide to the 2nd and 4th boundary harmonic excitation frequencies, which eventually leads to the vibration resonance of 4# catenary.

With the same simulation method, the maximum vibration amplitudes of 1# to 4# catenaries are shown in Fig. 10, which are based on the boundary deflection displacements in Table 2 with imbalance coefficient $b_i$ varying from 0.84 to 1.14.

When $b_3=b_4=$0.895, the maximum simulated vibration amplitude of 3# and 4# catenaries are 165 mm and 201 mm. The sum is 366 mm and larger than the 350 mm design distance between 3# and 4# catenaries, subsequently, the 3# and 4# catenaries could collide with each other just as it happened in reality. When the tension equilibrator functions normally and $b_4=$1, even with the largest boundary excitation displacement, the maximum displacements of 4# catenary is 53.6 mm and remains within the safe range of vibration.

Fig. 94# catenary vibration amplitudes and natural frequencies with varying imbalance coefficient

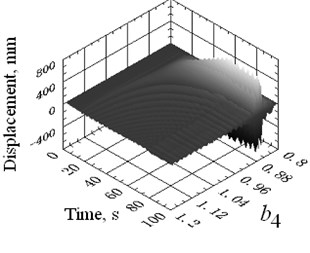
a) 3D surface graph of displacement

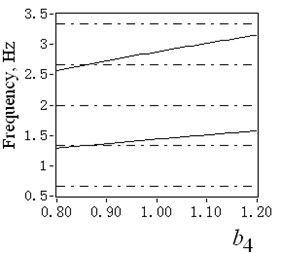
b) Transverse natural frequencies

Fig. 10Maximum displacement amplitudes of 1# to 4# catenaries with varying imbalance coefficient

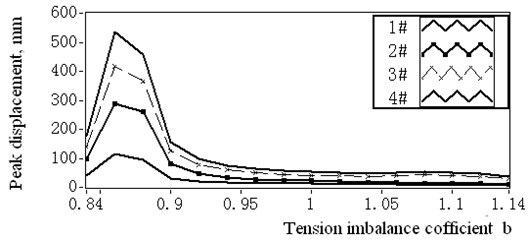
When $b_4$ varies from 0.895 to 1, the first natural frequency of 4# catenary changes from 1.36 Hz to 1.47 Hz and goes away from the boundary harmonic excitation frequency 1.34 Hz. Also the maximum simulated vibration amplitude decreases magnificently from 201 mm to 53.6 mm. It can be interpreted that the tension variation excitation played a vital role to change the resonance status and reduce the vibration displacement.

4.2.3. Fault diagnosis and experimental validation

Considering the above analysis, it is reasonable to assume that the major factor leading to the catenaries' large parametric transverse vibration could be tension variation excitations. In this sense, the malfunction of the tension equilibrator generates tension variation of the four catenaries, and changes its natural frequencies to coincide to boundary harmonic excitation frequencies, which eventually leads to transverse resonance vibration. In order to reduce the vibration amplitude, the tension equilibrator must be repaired even be replaced to maintain the tension balancing status.

After the tension equilibrator was replaced, its oil pressure reflecting the balance condition was measured and proved to be normal. The maximum vibration displacements amplitude of 4 catenaries under the balanced tension circumstance were measured again and listed in Table 5, from 1# to 4# as 22 mm, 35 mm, 51 mm and 67 mm. In order to reduce the transverse vibration amplitude of catenaries to normal level, the head sheave was replaced by a new one to reduce its axial deflection displacement. The vibration displacements of the head shave grooves along with catenary vibration amplitudes were measured again, the time domain and spectrum diagram of catenaries transverse vibrations were shown in Fig. 11. The statistical data were presented in Table 5.

Table 5Measured and simulation results of maximum catenaries vibration amplitudes after the head sheave and the tension equilibrator were replaced

Catenary and head sheave numbers	Measured deflection displacement amplitudes of head sheave (mm)	Simulated maximum amplitudes of catenaries (mm)	Measured maximum amplitudes of catenaries (mm)
1#	1.4	6.1	18
2#	1.8	12.2	30
3#	1.45	10	26
4#	1.5	10.6	25

Fig. 11Time domain and spectrum diagram of catenaries transverse vibrations after the head sheave and tension equilibrator was replaced (1# to 4#)

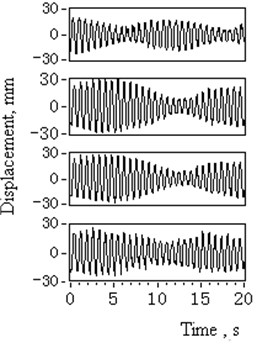
a) Time domain signal

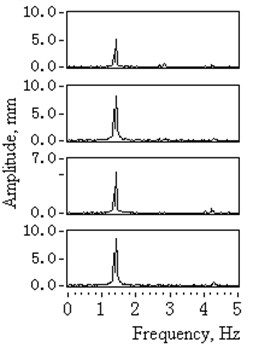
b) Amplitude spectrum

Table 5 and Fig. 11(a) show that even the measured maximum catenary vibration amplitudes differ from that of simulation ones. They have been minimized to normal range. Fig. 11(b) shows that the main vibration frequency has transferred from resonance state frequency 1.34 Hz to its new natural frequency 1.42 Hz. These measured results provide evidence that the resonance vibration of catenaries should be attributed to the severe tension imbalances and boundary displacement excitations, which are caused by the malfunction of the tension equilibrator and the over-limit head sheave groove deflection displacements.