Instability and resonance analysis of a beam subjected to moving mass loading via incremental harmonic balance method

1. Introduction

A substantial variety of practical systems in engineering can be represented as a flexible beam carrying a moving mass. Many applications such as motion of vehicles or trains on bridges, cranes transporting loads along its span, robotic arms, fluid transfer pipe systems, space structures and high speed machining processes are some of these systems, to enumerate a few. Therefore, determining dynamic behavior of a beam subjected to moving mass has been an interesting subject of investigation for a long time. Historically, the first known attempts to solve a moving load problem arose in the study of the collapse of Chester Railway Bridge by Willis [1] and Stokes [2]. After that, there have been a lot of efforts in this field, including the investigations done by Ayre and Jacobson [3] and two well known monographs by Inglis [4] and Hillerborg [5]. Recently, two books have been published by Fryba [6] and Yang et al. [7]. The growing usage of heavy and rapid truck vehicles besides the employment of lighter and more flexible structures have drawn engineers attention on terms which were not considered in the past [8-17].

Studies about the dynamic behavior of transiting objects across flexible beams can be classified into two major groups. The first group studies dynamic behavior of a beam under moving mass transition in time and/or frequency domain, focusing mainly on simulations and numerical methods. The second group mainly focuses on the analysis of system stability. This latter involves identification of system parameters for which system’s instability occurs or finding the resonance frequencies in presence of external excitation. These analyses usually conclude to the determination of stability boundary curves by semi-analytical or numerical methods. Despite numerous published papers for finding dynamic response of such systems, the number of investigations on the conditions for dynamic stability is restricted. Nelson and Conover [18] utilized the Floquet theory to determine the parametric regions of stability of a simply-supported Euler-Bernoulli beam lying on a uniform elastic foundation excited by a continuous series of equally-spaced mass particles. Benedetti [19] pointed out that in Nelson and Conover’s study, multiple separate regions of instability may appear and just for certain combinations of particle intervals and foundation moduli, single instability region occurs. Katz et al. [20] studied the dynamic stability and transverse vibration of a simply supported beam subjected to a deflection dependent moving load caused by the cutting forces in machining operations. Aldraihem and Baz[21] investigated dynamic stability of a stepped beam subjected to a moving mass. They used the impulsive parametric excitation theory to find the stable range for beam’s parameters when subjected to periodic parametric excitations. Verichev and Metrikine [22] studied the stability of vibrations induced by a moving mass along a beam lying on a periodically inhomogeneous continuous foundation using perturbation analysis. Mackertich [23] studied the dynamic stability of an elastically supported Timoshenko beam under travelling masses. He utilized the Floquet theory to determine regions of stability in the parameters plane.

It should be noted that all previous related studies on dynamic stability of the beam-moving mass problem just introduced the boundary curve that separates stable and unstable regions in the parameters plane. Although some references [6, 24-26] studied the problem of repetitive moving forces crossing the beam and identified those velocities of the force that conclude in resonance of the beam, to the best of the author's knowledge, the resonance analysis of a beam excited by moving masses has not been addressed before in open literature.

In this study, the mathematical model for a simply supported beam excited by a continuous sequence of equally-spaced identical masses is presented. The Galerkin method is then used to discretize the spatial domain and to obtain the governing ordinary differential equation of motion. Next, the IHB method is used to analyze the resulted equation and an iterative approach is implemented to determine the boundary of instability and the resonance curves in the plane of moving mass parameters. Numerical simulations are employed to confirm the correctness of the resulted curves.

2. Mathematical modeling and derivation of equation of motion

Fig. 1Schematic of a flexible beam-moving mass problem

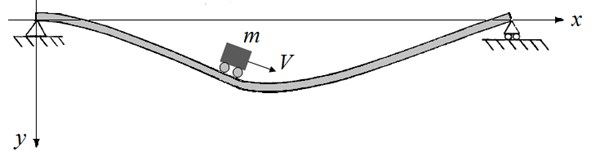
The system under consideration, which is composed of a traversing mass $m$ and a simply supported uniform Euler-Bernoulli beam of length $l$, mass density $\rho$, cross-sectional area $A$ and flexural rigidity $EI$, is schematically shown in Fig. 1. The purpose of investigating a flexible system influenced by repetitive mass transition is to deal with a time-varying system on which stability and parametric resonance studies can be performed comprehensively. Due to time-varying identity, such systems can exhibit unexpected phenomena that may occur in practice.

It is assumed that the mass moves along the beam from left to right with a constant velocity $V$ and remains always in contact with the beam. The governing equation that describes small vertical vibration of the beam represented by $v(x,t)$, can be written as [25]:

where $g$ is the gravitational acceleration and $\delta$ is the Dirac delta function.

In order to apply Galerkin method to discretize Eq. (1), the solution is considered as being expressible by the following expansion:

where $q_i\left(t\right)$ is the corresponding influence coefficient for the $i$th shape function ${\phi }_i\left(x\right)$ of the undamped beam modes (without the moving mass), defined by:

Substituting Eq. (2) into Eq. (1), then multiplying the resultant equation by the $j$th shape function ${\phi }_j\left(x\right)$, next integrating over the beam length and considering the orthogonality condition between modes, the partial differential Eq. (1) is converted to a set of ordinary differential equations on the modal coordinates described by:

where $\mathbf{q}=\left[q_1\right(t),\mathrm{}{q}_2(t),...,q_n(t){]}^T$ is the array of the modal coordinates. The matrix components are expressed as:

where ${\delta }_{ij}$ and ${\omega }_i$ are the Kronecker delta and the $i$th natural frequency of a simply supported beam $\left({\omega }_i={\left(i\pi /l\right)}^2\sqrt{EI/\rho A}\right)$, respectively. Considering one mode, the equation governing the modal coordinate becomes:

To rewrite the governing equation in dimensionless form, non-dimensional parameters are defined as:

Using the chain rule and the non-dimensional parameters given in Eq. (7), the dimensionless equation results as:

where dot denotes derivation with respect to $\tau$.

Eq. (8) consists of a linear equation whose coefficients vary with time up to the moment that the moving mass is still on the beam span. As soon as it leaves the beam span, the mass will have no more influence on the beam and consequently the time-varying coefficients of the governing Eq. (8) will vanish ($\alpha =\text{0}$), resulting in the removal of any vibration amplification factor. By considering the following sequence that once a mass leaves the beam, the next one enters the beam span and consequently results in a repetitive excitation, coefficients of Eq. (8) become periodical with period $T_p=l/V$. Performing Fourier expansion of the coefficients of Eq. (8) leads to:

To study the dynamic stability of the system, the right hand side of Eq. (9) is momentarily disregarded, which follows as:

3. Incremental harmonic balance method

IHB method represents an ingenious technique for establishing dynamic stability, applicable to the most general form of differential systems. According to IHB method, $\text{(}{\alpha }^{\mathrm{*}}\text{,}{\mathrm{\Omega }}^{\mathrm{*}}\text{)}$ is considered as a point on the merge of instability corresponding to a periodic solution $Q^{\mathrm{*}}\left(\tau \right)$ of Eq. (10). A neighboring point on this boundary is denoted by:

Substituting Eq. (11) into Eq. (10) and maintaining linear terms of $\mathrm{\Delta }Q\left(\tau \right)$, $\mathrm{\Delta }\alpha$ and $\mathrm{\Delta }\mathrm{\Omega }$, the linear incremental equation is obtained as:

where:

is the corrective term and will go to zero on instability boundary points [27]. The next step of the IHB method is to find an approximate solution by applying Galerkin's method. The unknown periodic solution $Q^{\mathrm{*}}$ can be expanded into a truncated Fourier series as:

Accordingly, $\mathrm{\Delta }Q$ is expressed as:

For conciseness, the functions $Q^{\mathrm{*}}$ and $\mathrm{\Delta }Q$ can be written as:

where:

Applying the Galerkin procedure to Eq. (12) yields:

Substituting the terse form of Eq. (16) into Eq. (18), a set of linear equations containing $\mathrm{\Delta }\mathbf{A}$, $\mathrm{\Delta }\alpha$ and $\mathrm{\Delta }\mathrm{\Omega }$ as main variables are obtained as:

where:

Eq. (19) is utilized to obtain the instability boundary. It is a set of nonlinear equations in terms of ${\alpha }^{\mathrm{*}}$, ${\mathrm{\Omega }}^{\mathrm{*}}$ and ${\mathbf{A}}^{\mathrm{*}}$. Instead of solving these nonlinear equations for ${\alpha }^{\mathrm{*}}$, ${\mathrm{\Omega }}^{\mathrm{*}}$ and ${\mathbf{A}}^{\mathrm{*}}$, a set of equations which are linear in terms of $\mathrm{\Delta }\mathbf{A}$, $\mathrm{\Delta }\alpha$ and $\mathrm{\Delta }\mathrm{\Omega }$ are solved in a recursive approach.

In Eq. (19) the number of unknown variables exceeds the number of equations by two. Yet, since in vector ${\mathbf{A}}^{\mathrm{*}}$ only the relative values of the coefficients are needed, it is possible to prescribe one of them as a unity reference constant with its corresponding increment in $\mathrm{\Delta }\mathbf{A}$ equal to zero. Also by selecting one parameter out of $\alpha$ or $\mathrm{\Omega }$ as the active parameter and consequently setting its increment equal to zero (i.e., $\mathrm{\Delta }\alpha =\text{0}$ or $\mathrm{\Delta }\mathrm{\Omega }=\text{0}$), two unknowns are already set as zero and the equations can be solved for the rest.

As explained, let us select $\alpha$ as the active parameter and set $\mathrm{\Delta }\alpha$ and the $i$th element of $\mathrm{\Delta }\mathbf{A}$ equal to zero. Then ${\mathrm{\Omega }}^{\mathrm{*}}$ and ${\mathbf{A}}^{\mathrm{*}}$ are found through the following recursive algorithm:

1) Select ${\alpha }^{\mathrm{*}}$.

2) Select initial values for ${\mathrm{\Omega }}^{\mathrm{*}}$ and ${\mathbf{A}}^{\mathrm{*}}$.

3) Solve the following linear equation:

where ${\tilde{\mathbf{S}}}_{\mathrm{\Delta }A}$ is the modified form of ${\mathbf{S}}_{\mathrm{\Delta }A}$ by eliminating its $i$th column and $\mathrm{\Delta }\tilde{\mathbf{A}}$ is the changed form of vector $\mathrm{\Delta }\mathbf{A}$ by removing its $i$th element.

4) Check for convergence of the solution by examining $‖\mathbf{R}‖\le \epsilon$, where $\epsilon$ is an enough small number.

5) Update ${\mathrm{\Omega }}^{\mathrm{*}}$ and ${\mathbf{A}}^{\mathrm{*}}$ as ${\mathrm{\Omega }}_{New}^{\mathrm{*}}={\mathrm{\Omega }}^{\mathrm{*}}+\mathrm{\Delta }\mathrm{\Omega }$ and $A_{New}^{\mathrm{*}}=A^{\mathrm{*}}+\mathrm{\Delta }A$ if needed and repeat the procedure from step 2 if convergence is not reached.

6) Select a new value for ${\alpha }^{\mathrm{*}}$ and repeat steps 1 to 5 to determine the corresponding ${\mathrm{\Omega }}^{\mathrm{*}}$ and ${\mathbf{A}}^{\mathrm{*}}$.

By considering series expansion of different order for the solution, convergence of the instability boundary curve and other resonance curves can be expected with arbitrary accuracy. All these curves are determined through the above-mentioned iterative procedure.

4. Results and discussion

4.1. Dynamic stability

Results of dynamic stability investigation for a simply supported Euler-Bernoulli beam excited by a continuous sequence of identical equally spaced moving masses are presented in this section. According to Floquet theory for $T$-periodic systems, the solutions corresponding to the transition curves that separate stable and unstable regions in the parameters plane are of either $T$ or 2$T$ period. Therefore, the following series expansions are considered for $Q^{\mathrm{*}}\left(\tau \right)$ and $\mathrm{\Delta }Q\left(\tau \right)$ to represent the $T$-periodic solution:

22

$\begin{array}{l}{Q}^{\mathrm{*}}=\sum _{p=0,\mathrm{}2,\mathrm{}4,\mathrm{}...}\left[a_p\mathrm{c}\mathrm{o}\mathrm{s}\left(p\tau \right)+b_p\mathrm{s}\mathrm{i}\mathrm{n}\left(p\tau \right)\right],\mathrm{}\mathrm{}\mathrm{}\\ \mathrm{\Delta }Q=\sum _{p=0,\mathrm{}2,\mathrm{}4,\mathrm{}...}\left[\mathrm{\Delta }{a}_p\mathrm{c}\mathrm{o}\mathrm{s}\left(p\tau \right)+\mathrm{\Delta }{b}_p\mathrm{s}\mathrm{i}\mathrm{n}\left(p\tau \right)\right],\end{array}$

and also the following expansions for the 2$T$-periodic solution:

23

$\begin{array}{l}{Q}^{\mathrm{*}}=\sum _{p=1,\mathrm{}3,\mathrm{}5,\mathrm{}...}\left[a_p\mathrm{c}\mathrm{o}\mathrm{s}\left(p\tau \right)+b_p\mathrm{s}\mathrm{i}\mathrm{n}\left(p\tau \right)\right],\mathrm{}\mathrm{}\\ \mathrm{\Delta }Q=\sum _{p=1,\mathrm{}3,\mathrm{}5,\mathrm{}...}\left[\mathrm{\Delta }{a}_p\mathrm{c}\mathrm{o}\mathrm{s}\left(p\tau \right)+\mathrm{\Delta }{b}_p\mathrm{s}\mathrm{i}\mathrm{n}\left(p\tau \right)\right].\end{array}$

The trend consists of finding those parameters of traversing mass in $(\mathrm{\alpha }-\mathrm{\Omega })$ plane which result to a periodic response for Eq. (10), hence establishing the boundary curve iteratively. This curve, which separates stable and unstable regions in the system parameters plane, is depicted in Fig. 2. As shown, the regions above and below this curve display unstable and stable behavior, respectively. In order to verify the validation of the IHB method, this curve is compared to the one resulted by Floquet theory. Coincidence of these two curves proves the accuracy of the analysis performed by presented procedure.

Fig. 2Stable and unstable regions from IHB method (five term expansion) and Floquet theory

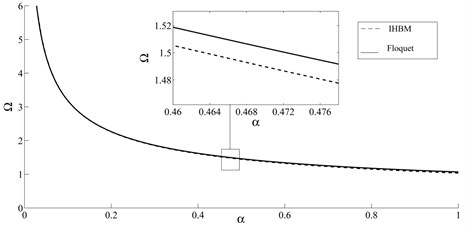
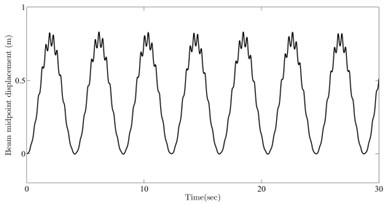
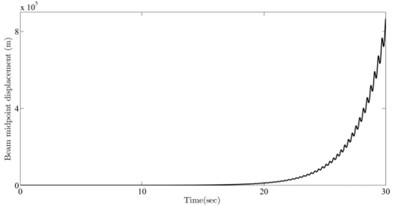
Fig. 3Vibration simulation for parameters selected in the vicinity of the a) stable and b) unstable sides

a)

b)

Fig. 3 depict the numerical simulations of the beam mid-span deflection (i.e. $v\left(0.5l,t\right)={\phi }_1\left(0.5l\right)q_1\left(t\right)$) for two sets of numerical values of $(\mathrm{\alpha }-\mathrm{\Omega })$ from stable and unstable regions. Beam parameters are selected as $EI=$5×10⁵ N.m², $\rho A=\text{10}\text{kg/m}$ and $l=$20 m. The operational set points $\text{(}\mathrm{\alpha }=\text{0.3,}\mathrm{}\mathrm{\Omega }=\text{1.76)}$ and $\text{(}\mathrm{\alpha }=\text{0.3,}\mathrm{}\mathrm{\Omega }=\text{1.86)}$ belong to the stable and unstable regions, respectively. The corresponding stable and unstable behavior of the system can be seen in Fig. 3. It should be noticed that although there is an apparent damping term in the equation, nonetheless the solution in the stable region does not diminish to zero but remains bounded as predicted by Floquet theory.

4.2. Occurrence of resonance in stability region

In this section, the conditions under which the moving mass transition conducts to external resonance in the system are investigated. It is revealed that there are some curves lying in the stable region leading to situations where the beam experiences vibrations of growing amplitudes.

The superposition principle for linear time-varying systems permits us to consider separately each term on the right-hand side of Eq. (27) as a plausible exciting term that may induce resonance in the system. It is claimed that if a solution can be synchronized with one of those excitation terms, similar to time-invariant systems, resonance can occur. Indeed, the definition of natural frequency is extended here for a time-varying system as the frequency of its homogeneous response, like for time-invariant systems. By this way, those parameters of the moving mass are being sought which generate a solution with principal frequency corresponding to one of the excitation frequencies. In order to fulfill this condition, let's consider a periodic solution with the same principal period as the k-th excitation term:

24

$\begin{array}{l}{Q}^{*}=\sum _{p=k,k+1,k+2,...}\left[a_p\mathrm{c}\mathrm{o}\mathrm{s}\left(2p\tau \right)+b_p\mathrm{s}\mathrm{i}\mathrm{n}\left(2p\tau \right)\right],\\ \mathrm{\Delta }Q=\sum _{p=k,k+1,k+2,...}\left[\mathrm{\Delta }{a}_p\mathrm{c}\mathrm{o}\mathrm{s}\left(2p\tau \right)+\mathrm{\Delta }{b}_p\mathrm{s}\mathrm{i}\mathrm{n}\left(2p\tau \right)\right].\end{array}$

As discussed, the IHB method permits to design a response which matches one of the excitation terms and consequently realizes the conditions for resonance. The expected resonance curve can be obtained by following the procedure explained in section 3. Through increasing $k$, different candidate solutions corresponding to other excitation terms can be generated, resulting to multiple resonance curves shown in Fig. 4. More concisely, those values of mass-speed parameters in the $(\mathrm{\alpha }-\mathrm{\Omega })$ plane lying on these curves will cause resonance in the system.

Fig. 4Resonance curves located in the stable region

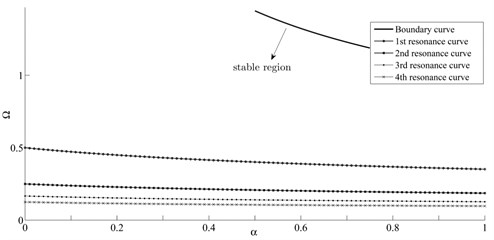
Although these resonance curves have not been addressed in previous studies, their intersection with vertical axis, corresponding to moving load transition $\text{(}\mathrm{\alpha }=\text{0)}$, have been reported in [25] as:

25

${\mathrm{\Omega }}_{\mathrm{r}\mathrm{e}\mathrm{s}.}=\frac{1}{2n},n=1,2,3,\dots ,$

as it is verified in Fig. 4.

In order to further validate the obtained results, numerical simulations of the beam mid-span deflection (i.e. $v\left(0.5l,t\right)={\phi }_1\left(0.5l\right)q_1\left(t\right)$) are provided using four sets of numerical values for $\mathrm{\alpha }$ and $\mathrm{\Omega }$ located on these resonance curves, namely $\text{(}\mathrm{\alpha }=\text{0.3,}\mathrm{\Omega }=\text{0.4302)}$, $\text{(}\mathrm{\alpha }=\text{0.3,}\mathrm{\Omega }=\text{0.2198)}$, $\text{(}\mathrm{\alpha }=\text{0.3,}\mathrm{}\mathrm{\Omega }=\text{0.1480})$ and $\text{(}\mathrm{\alpha }=\text{0.3,}\mathrm{}\mathrm{\Omega }=\text{0.1115)}$. Fig. 5 depicts the simulation results for beam mid-span response. As seen from the figures, selected parameters for the moving mass cause resonant behavior in the beam. It is worth noting that such intermittent resonance conditions appearing for a determined mass ratio were not expected in practice.

Fig. 5Beam midpoint response for parameters selected from a) 1st, b) 2nd, c) 3rd, d) 4th resonance curve

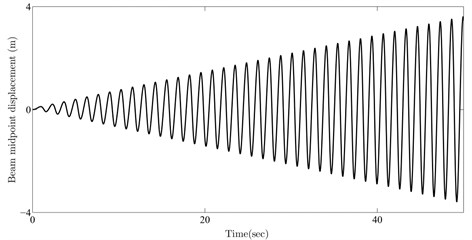
a)

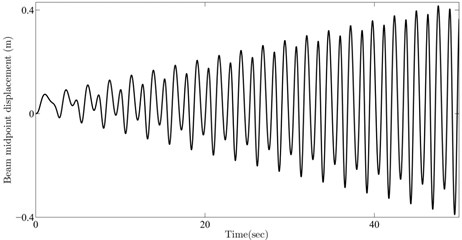
b)

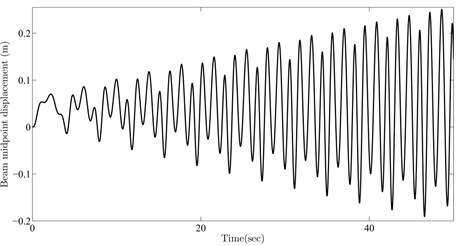
c)

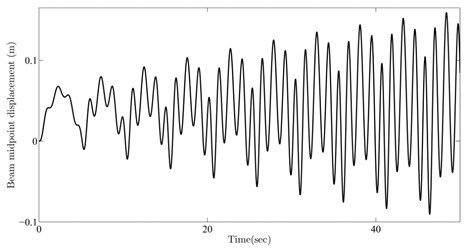
d)

5. Conclusions

In the present study, the problem of dynamic stability of a simply supported Euler-Bernoulli beam under the periodic loading of sequential moving masses is investigated by adopting the IHB method. The resulted instability curve, which separates the stable and unstable regions, is verified by comparing with the one derived by applying Floquet theory. In addition, by employing above method, curves describing resonance conditions in the stable parameter region are depicted. These curves, in fact, represent those moving mass parametric values that yield resonance in the beam response. Numerical simulations verify the occurrence of resonance for the parameters selected on these curves.