Dynamic stress prediction method for rubbing blades

2.1. Centrifugal forces

The modern turbomachinery has characteristics of large-scale and high speed. When the rotor rotates in high-speed, a quite small unbalance can cause quite large centrifugal inertial forces. Therefore, the effect of centrifugal forces on dynamic analysis of blade-rotor systems is indispensable. However, the mathematical model of centrifugal force vector must be given in order to solve conveniently by using the analytic method. So in our study, we proposed a method for obtaining the centrifugal force vector.

Firstly, establishing the finite element model of the blade, and a modal analysis is conducted to export the Harwell-Boeing matrices, which can be formed into the mass matrix $\mathbf{M}$, the damping matrix $\mathbf{C}$, and the stiffness matrix $\mathbf{K}$ using the matrix assembly techniques. Then, applying a rotating speed along axial direction, the static deformation $\left\{{\mathbf{x}}_0\right\}$ of the rotating blade is obtained through a static analysis in ANSYS. Lastly, the centrifugal force vector ${\mathbf{P}}_c$ is follow obtained by ${\mathbf{P}}_c=\mathbf{K}\bullet \left\{{\mathbf{x}}_0\right\}$.

2.2. Rubbing forces

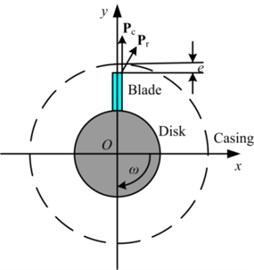
To improve the performance and efficiency of rotating machinery, a widely used way is to reduce the clearance between the blade and the casing. However, the rubbing fault is being liable to happen thereupon. In the paper, a schema of blade-casing rubbing is depicted in Fig. 1, in which $e$ is the static clearance between the moving blade and the static casing. The blade-casing rubbing fault will happen when the radial displacement of blade tip exceeds e with the effects of centrifugal forces at a rotation speed or other factors (misalignment, thermal bending, etc.).

In our study, the fixed-point rubbing is taken into account. The rubbing force is denoted by the piecewise-linear elastic model. The nonlinear resilience can be expressed as the following:

where $k_{ni}$ is the nonlinear contact stiffness; $e_i$ is the rubbing clearance.

Assuming that there is only one rubbing location at the $i$th DOF in the totally $n$ DOFs system, the rubbing force vector can be described as:

Fig. 1Schema of the blade-casing rubbing

2.3. Dynamic model of the rubbing blade system

Considering the effects of rubbing and centrifugal forces, the differential equation of motion of a rotating rubbing blade system can be written as follow:

where $\mathbf{M}$, $\mathbf{C}$, $\mathbf{K}$ and $\mathbf{X}$ respectively denote the mass matrix, the damping matrix, the stiffness matrix, and the displacement vector of the system; ${\mathbf{P}}_c$ is the centrifugal force vector; and ${\mathbf{P}}_r$ is the rubbing force vector. The dynamic model of the rubbing blade is now established for finding a solution of the system.

3.1. Dynamic stress prediction method

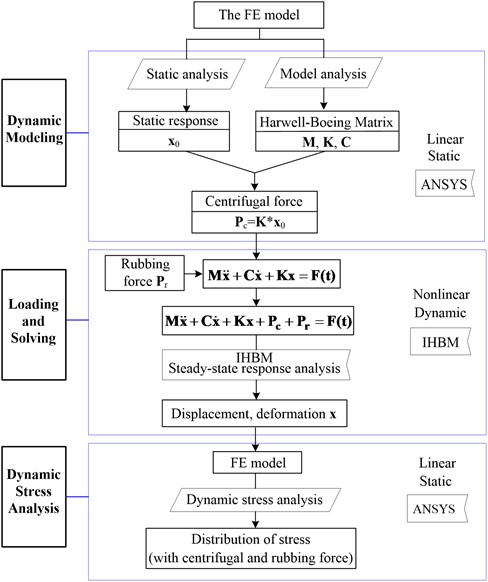
In this section, we present a new way for predicting the dynamic stress on a rubbing blade, which combines the IHB method with the FEM. To describe more clearly, the algorithm flow diagram is established as shown in Fig. 2, and it can be detailed into the following three steps of the solution procedure.

First, dynamic modeling: according to the method referring in Section 2.1, form matrices $\mathbf{M}$, $\mathbf{C}$, $\mathbf{K}$, and static response $\left\{{\mathbf{x}}_0\right\}$ of the system, and the centrifugal force vector is then obtained by ${\mathbf{P}}_c=\mathbf{K}\bullet \left\{{\mathbf{x}}_0\right\}$; the nonlinear equation of motion of the blade system is established by using Lagrange equation considering the effect of centrifugal force and rubbing force, seeing in Section 2.3.

Next, loading and response solving: the steady-state response $\left\{\mathbf{x}\right\}$ at any time of the differential equation was solved by applying the IHB method, that is the transient displacement and deformation at each node of the rubbing blade, is obtained;

Third, dynamic stress determination: taking the transient displacement at each node obtained as initial displacement constraints, imposing the deformation of each point on corresponding node of the blade, then the dynamic stress at any time and location can be predicted through a static analysis in ANSYS, whereas accounting for the effects of centrifugal force and rubbing force.

Since the transient finite element analysis is transformed into the static analysis in the present method, it significantly raises the solution efficiency. Moreover, compared to the numerical integration method employed in ANSYS, the IHB method can easily and directly solve the steady-state response of strongly nonlinear vibrations.

Fig. 2Algorithm flow diagram for dynamic stress prediction of rubbing blades

3.2. IHB method

As the IHB method is an effective tool for obtaining periodic solutions of strongly nonlinear multi-DOF systems, which is applied to conduct the rubbing problem to improve the efficiency of the prediction method.

In this subsection, the IHB method is formulated to analyze $N$ DOF nonlinear system vibrations. The dynamic equation of motion of a rubbing blade system is generally expressed as:

where a dot denotes differentiation with respect to the new dimensionless time variable $\tau$, which is defined as $\tau =\omega t$; the connotations of symbols in the equation as what mentioned before in Eq. (3).

Considering the steady-state response of Eq. (4) and supposing the base frequency of the response is $1/q$, and $q$ is a positive integer. Considering the $r$th order harmonic, the response of node $i$ can be expanded to the form of a Fourier series:

All solutions of the $N$ DOF system are $\mathbf{X}=\sum _{l=0}^r{\mathbf{X}}_l={\left[\begin{array}{lll}{x}_1& \cdots & x_N\end{array}\right]}^{\mathrm{T}}$, where ${\stackrel{-}{\mathbf{X}}}_l$ denotes the $l$th harmonic of $\stackrel{-}{\mathbf{X}}$.

Supposing $\mathrm{\Delta }\mathbf{X}$ is the increment of $\mathbf{X}$ yields:

Then, from Eq. (5), the following can be obtained:

where:

Let $\mathbf{S}=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left[\begin{array}{llll}{\mathbf{C}}_s& {\mathbf{C}}_s& \cdots & {\mathbf{C}}_s\end{array}\right]$ and $\mathbf{A}={\left[\begin{array}{llll}{\mathbf{A}}_1^{\mathrm{T}}& {\mathbf{A}}_2^{\mathrm{T}}& \cdots & {\mathbf{A}}_N^{\mathrm{T}}\end{array}\right]}^{\mathrm{T}}$. Therefore, $\mathbf{X}=\mathbf{S}\mathbf{A}$, and all compositions of unknown quantity are the following:

Substituting Eq. (6) into Eq. (4) and neglecting the high-order harmonic components, this yields:

where ${\mathbf{C}}_n=\partial {\mathbf{P}}_r/\partial \dot{\mathbf{X}}$ and ${\mathbf{K}}_n=\partial {\mathbf{P}}_r/\partial \mathbf{X}$.

Assume that $\delta \mathbf{X}=\mathbf{S}\delta \mathbf{A}$ is the variation of $\mathbf{X}$. Applying the Galerkin’s method, Eq. (9) yields:

Let ${\mathbf{M}}_s=\mathbf{M}\ddot{\mathbf{S}}$, ${\mathbf{C}}_s=\mathbf{C}\dot{\mathbf{S}}$, ${\mathbf{K}}_s=\mathbf{K}\mathbf{S}$, ${\mathbf{C}}_{ns}={\mathbf{C}}_n\dot{\mathbf{S}}$, and ${\mathbf{K}}_{ns}={\mathbf{K}}_n\mathbf{S}$. Based on the variation characteristic, Eq. (4) can be rewritten as:

where:

$\mathbf{A}$ can be solved from Eq. (11) iteratively, following which $\mathbf{X}$ can be obtained.

4.1. Finite element analysis model of the blade

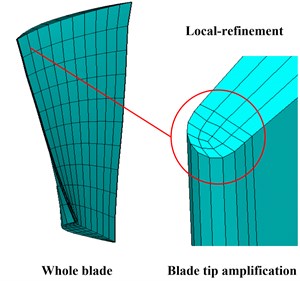
In the paper, the finite element model of a twisted 3D blade was developed by using the ANSA, as shown in Fig. 3. In order to calculate more precise, local mesh refinement at blade edges was adopted. Assuming the rotating speed of the blade is 10000 rpm and its material parameters are detailed in Table 1. The finite element model is divided into 1023 nodes with 720 Solid185 elements, which has three DOFs at each node: translations in the nodal $x$, $y$ and $z$ directions.

Fig. 3Finite element model of the blade

4.2. Algorithm verification

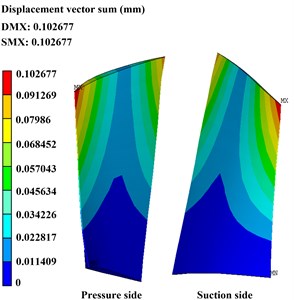
To illustrate the precise of the present method, contrast verification has been carried out. Figs. 4 and 5 show the deformation and stress distribution of the blade with centrifugal force obtained from the ANSYS directly and the present method, respectively. Precise comparison of the two methods is detailed in Table 2.

There are 0.327 % and 0.077 % error percentage in the maximum value of deformation and stress obtained from the present method compare to the ANSYS. The tiny error generally can be neglected and it may be caused by truncation error of calculation, which depends on the selected harmonic terms in the IHB method. Comparison with the ANSYS shows that the calculation results are almost identical, which indicates that this method is a feasible one.

Fig. 4Deformation and stress distribution of the blade with centrifugal force obtain by ANSYS

a) Deformation

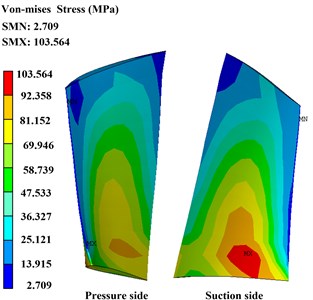
b) Stress distribution

Fig. 5Deformation and stress distribution of the blade with centrifugal force obtain by the present method

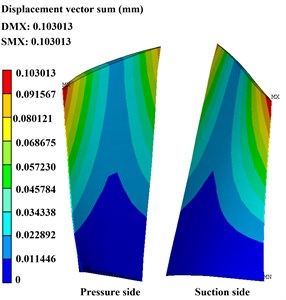
a) Deformation

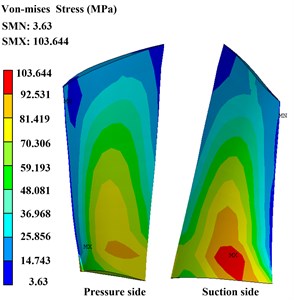
b) Stress distribution

4.3. Effect of contact stiffness

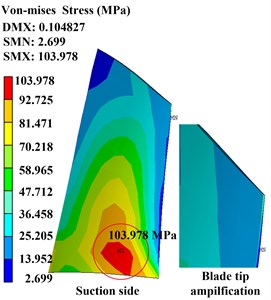
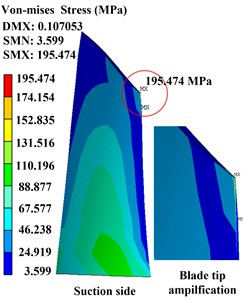
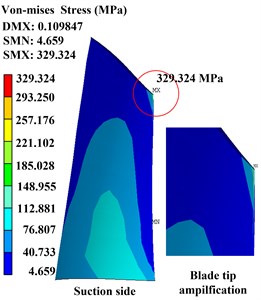
The nonlinear contact stiffness is an important rubbing parameter that can affect the severity of rubbing fault. In this subsection, we firstly study the effects of nonlinear contact stiffness on stress distribution of the system, so the rubbing clearance is fixed as $e=$ 0.015 mm. Periodic solutions are solved by using the IHB method, and then stress distributions of the rubbing blade surface are obtained by the present prediction method. Assuming that the rubbing contact occurs at the left blade tip in the pressure side, which is the max deformation location; the time-domain waveforms of the rubbing node are shown in Fig. 6(a) and the Von-Mises stress of the blade with different contact stiffness are shown in Fig. 6(b) to (d) which corresponding to 1×10³ N/mm, 2×10³ N/mm, and 3×10³ N/mm.

As shown in Fig. 6(a), the obvious distortion is induced by the blade tip rubbing fault in time-domain waveforms. More concretely, the amplitude amplification on one side happens with relatively smaller contact stiffness, whereas the wave clipping phenomenon on one side appears with relatively larger contact stiffness.

It is also found that, from Fig. 6(b) to (d), when the contact stiffness reaches 1×10³ N/mm, stress distribution on blade surface changes seriously due to the rubbing fault. The max Von-Mises stress on the whole blade surface increases about 100 MPa when the contact stiffness increases by 1×10³ N/mm; the max value on blade tip changes from 103.978 MPa to 329.324 MPa when the contact stiffness reaches into 3×10³ N/mm; the high stress area changes from the blade root location to the blade tip location. It is noted that the regions of high stress and dangerous points may occur not only at the blade root but also the blade tip locations.

Fig. 6Time-domain waveforms and distribution of Von-Mises stress with different contact stiffness

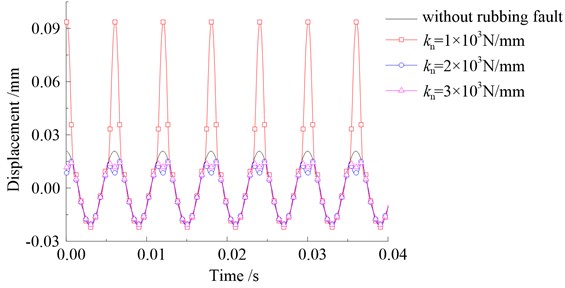
a)

b)$k_n=$1×10³ N/mm

c)$k_n=$2×10³ N/mm

d)$k_n=$3×10³ N/mm

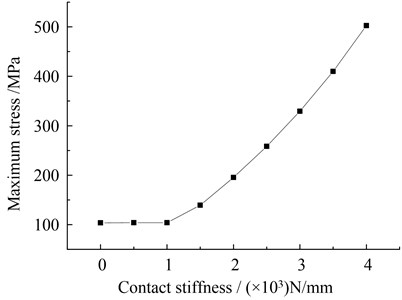
To demonstrate more clearly, the maximum Von-Mises stress curves with different contact stiffness are depicted in Fig. 7. As noted that the max value of the Von-Mises stress becomes larger with the increasing contact stiffness after the rubbing fault occur. It also indicates that the maximum value of Von-Mises stress becomes higher obviously when the rubbing fault becomes more serious.

Fig. 7Maximum Von-Mises stress curves with different contact stiffness

4.4. Effect of rubbing clearance

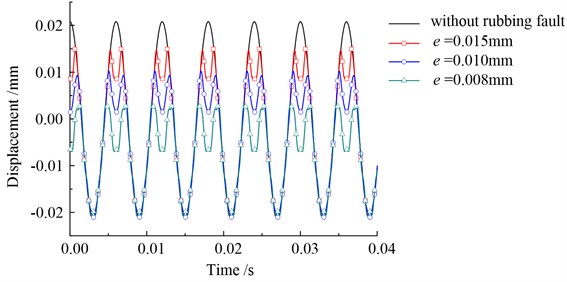
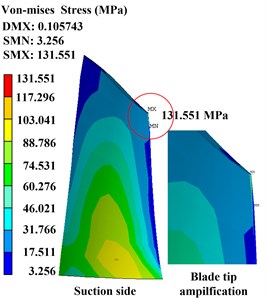
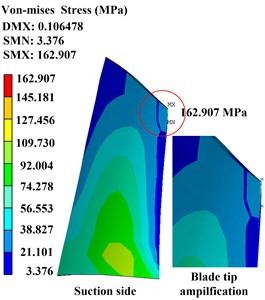
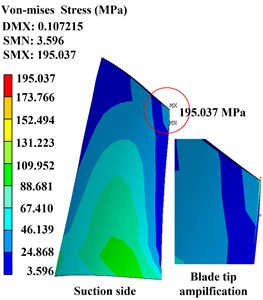
Moreover, the rubbing clearance is another key rubbing parameter, the effect of it on stress distribution is investigated in this subsection. It also assumed that the rubbing contact occurs at the same location, with a contact stiffness of 1×10³ N/mm. Fig. 8(a) displays the time-domain waveforms of the rubbing node with different rubbing clearances of 0.015 mm, 0.010 mm, and 0.008 mm. Fig. 8(b) to (d) presents the Von-Mises stress of the blade with different rubbing clearances of 0.012 mm, 0.010 mm, and 0.008 mm, respectively.

It can be seen from Fig. 8(a) that the wave clipping phenomenon on one side appears more serve with the rubbing clearance becomes smaller; the clearance can also seriously affect the distribution of stress on blade: the max stress on blade surfaces increases from 131.551 MPa to 195.037 MPa with the rubbing clearance changing from 0.012 mm to 0.008 mm; the max stress increases about 30 MPa when the rubbing clearance decreases by 0.002 mm. More obviously, the region of high stress also appears from the blade root location to the blade tip location.

Fig. 8Time-domain waveforms and distribution of Von-Mises stress with different rubbing clearance

a)

b)$e=$0.012 mm

c)$e=$0.010 mm

d)$e=$0.008 mm

Additionally, Fig. 9 displays the max Von-Mises stress curves of the blade with different rubbing clearances. As shown in the graph, the max stress on the blade displays a decreasing tendency with the increase in rubbing clearance. Due to that the rubbing fault is being liable to happen with the decreasing rotor-stator clearance, that is, the dynamic stress becomes larger when the rubbing fault becomes more serious.

4.5. Discussions

Here, we conduct numerical experiments for predicting dynamic stress of a rubbing blade by using the present method. From the preceding analysis, we can infer that the method is an efficient tool for performing dynamic stress analysis of rubbing blades, which combines the IHB method with the traditional FEM and therefore can save time required for solving the nonlinear steady-state response of systems. The advantage of this prediction method is high-efficiency.

Fig. 9Maximum Von-Mises stress curves with different rubbing clearance

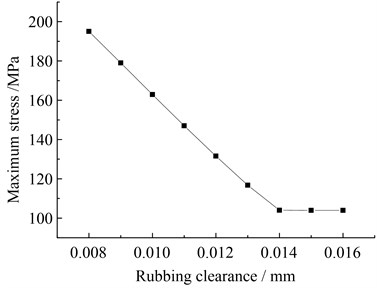
Moreover, the above numerical experiments denote that the blade tip rubbing fault can seriously affect the distribution of stress on blade surfaces. The max Von-Mises stress on the whole blade surface increases about 100 MPa when the contact stiffness increases 1×10³ N/mm; and it also increases about 30 MPa when the rubbing clearance decreases by 0.002 mm. It shows that the stress on blade increases sharply with the rubbing fault becomes serious; the region of high stress occurs from the blade root location to the blade tip rubbing location. Blade tip rubbing fault will not only induce complex nonlinear vibration, but also can cause plastic deformation and even break off if there is an initial crack on the blade, its stress distribution therefore should be predicted accurately. Meanwhile, the stress variation on the part of blade tip and blade root caused by rubbing fault should be given especially notice; it can also provide guidance of strength design according to the stress value in dangerous points.