Study on lateral vibration of rotary steerable drilling system

1. Introduction

In oil and gas drilling engineering, the well is created by drilling a hole 5 to 50 inches (127.0 mm to 914.4 mm) in diameter into the earth with a drilling rig that rotates a drillstring with a bit attached. It has a common problem of severe drillstring vibrations; since the drillstring consists of several drill pipes, drill collars, stabilizers and connections, which are under some heavy and complex dynamic loadings. Three forms of vibrations have been identified for drillstring are axial, torsional and lateral vibrations [1] (Fig. 1). The destructive nature of each type of vibration is different. If drillstring excites near one of its natural frequencies, it starts to absorb the energy. This energy boosts the amplitude of string vibration, increases bending and impacts with the borehole, and leads to early fatigue of tools and reduction of bit life.

Fig. 1Three forms of drillstring vibration

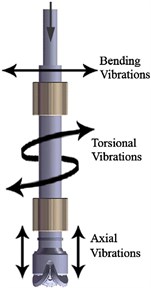
Lateral vibration have been undertaken extensive research since it proposed from mid-1960s, was considered the main reason that caused the fatigue failure of the bottom hole assembly (BHA) [2]. Many studies of the drillstring focused on the determination of natural frequencies [3, 4], bending stress calculation [5, 6], stability analysis [7] and lateral displacement prediction [8], etc. Spanos PD et al. [9] established the finite element model of drillstring lateral vibration, analyzed of nonlinear random vibration. The complexity of the problem and the development of fast new computers have opened the door to versatile numerical techniques. Several researchers have employed effective numerical methods such as finite difference method (FDM) and finite element method (FEM) to treat the problem. Khan [10] used the FDM to solve the axial and torsional vibrations of drillstring, while neglecting the added mass and damping effects. Rey [11] derived the differential equation of motion for lateral vibration of bottom hole assembly (BHA) between the bit and stabilizers, and solved it by FDM.

Additionally, in rotary steerable directional drilling system [12], depth study of the dynamical motion state of the BHA is very necessary and urgent. With the development of measurement while drilling (MWD) technology, it have been become the trend in recent years that the use of downhole measurement data to analyze the mechanical properties and vibration characteristics of the BHA [13]. Especially, we could obtain the data form the near-bit measurement [14], which is the technology that installs the measurement system near the drilling bit. Thus, we can analysis the drilling bit vibration that could be supported by the field data. However, there is no report describe the vibration characteristics of the drillstring with the measurement time series. This paper based on the simulation study of FDM, measured the drill bit lateral vibration real-time, the frequency up to 100 Hz. The system stored sampling data real-time in the drilling process, which could be play backed after drilling. Thus we can obtain the massive time series data of the drillstring vibration. Then we use time series analysis method to further study the dynamics of drillstring with measurement data.

2. Mechanical property of lateral vibration

One of the early attempts at FEM analysis of the drillstring was conducted by Millheim et al. [15], where the drillstring was modeled as a straight beam with beam and gap elements using an FEM package. The nodal displacement was derived using the variational principle to study drillstring deflection and bit forces. Straight and curved beam elements were compared in their model and the results were verified by field data.

The drillstring is assumed as a beam with two cross sections (collars and pipes). A planar wire shape sketch with hollow pipe profiles is used to model the entire drillstring. The “Hermite cubic” beam element is used, which does not account for the shear flexibility, although axial strain is considered. The drillstring-mud interaction effects on the drillstring dynamic analysis are important. The effect of inside-outside drillstring mud flow was investigated by Paidoussis et al. [16]. They found that the effect of internal and external mud flow is sensitive to the annular space between the drillstring and wellbore. When the fluid flow was considered in the dynamic equations, the lateral dynamic response was a bit larger initially. However, steady-state response was unchanged. The effect of fluid flow has not been considered in this study.

The partial differential equations of drillstring lateral vibration will be obtained according to the drillstring bending theory and D’Alembert’s principle [17]:

wherein, $a^2=EIg/A\rho$; $A$ is cross-sectional area of drillstring, $I$ is moment of inertia of drillstring, $\rho$ is density of drillstring material, $y$ is the deflection of the drillstring, $t$ is the time.

Study of the fundamental oscillation mode only, the displacement of each point on the axis is the harmonic function with respect to time, then:

where $X$ is a function of $x$, then:

Simultaneous Eqs. (2)-(5):

The general solution is:

wherein: $K=p^{2}A\mathrm{\gamma }/EIg$.

In the drilling process, assuming that vibration frequency proportional to the rotational speed, that is $n/60$, where $n$ is the rotational speed of drillstring. Then the angular frequency of vibration can be expressed as $n\pi /\text{30}$. Resonance will be occurs when the angular vibration frequency of drillstring is equal to its natural angular frequency $p$ (rad/s). So according to the Equation $p=n\pi /\text{30}$, the critical speed of drillstring will be obtained:

where $p_i$ is $i$th natural frequency of the lateral vibration, (rad/s).

Replaced $p_i$ (rad/s) by another expression $f_i$ (Hz), the Eq. (8) can be expressed as following:

where $f_i$ is $i$th natural frequency of the lateral vibration, (Hz).

3. Analysis of lateral vibration using finite element method

In this study, since the ANSYS software is used, there are two options for setting up the contact condition between the drillstring and the wellbore, as stated above. The analytical and FEM models are solved to derive the natural frequencies and response of the drillstring at certain points of interest. Predicting the resonance frequencies at the early stage of designing a drillstring and before each run is a crucial task to avoid the unwanted resonance states. If the working conditions stay close to the resonance state, the BHA absorbs energy, which amplifies lateral vibrations. These amplified vibrations, as a result of the transferred resonance energy, result in potentially catastrophic collisions of the BHA with the wellbore. Therefore, the very first step to reduce lateral vibrations and avoid successive contacts is to find resonance natural frequencies of the drillstring. The natural frequencies extracted from FEM model along the length of drillstring are shown in Table 1.

As shown in Table 1, the lateral vibration of drillstring at the bottom hole, the lower frequency decreases with the increase of its length. Since the drillstring lateral vibration frequency range is wide, the lateral vibration will definitely happen in the drill process at a certain fixed parameters. Additionally, lateral vibration of drillstring can be occurred in a single drillstring, a plurality of drillstring simultaneously as well.

As shown in Fig. 2, deformation maps of the first four mode shapes of lateral vibration were produced by ANSYS software, and Fig. 3 is the displacement nephogram of the first four mode shapes of lateral vibration. The maximum displacement occurs at node 44906 in the Fig. 2(a), in the position of the global coordinate system are: (7.0365, 0.2644, –0.0284). The maximum displacement occurs at node 35493 in the Fig. 2(b), in the position of the global coordinate system are: (2.81204, 0.3518, 0.121). The maximum displacement occurs at node 26954 in the Fig. 2(c), in the position of the global coordinate system are: (4.4207, 0.3518, 0.0450). The maximum displacement occurs at node 31024 in the Fig. 2(d), in the position of the global coordinate system are: (4.8398, 0.3518, 0.06).

Fig. 2The deformed plot of lateral vibration

a) 1 order

b) 2 order

c) 3 order

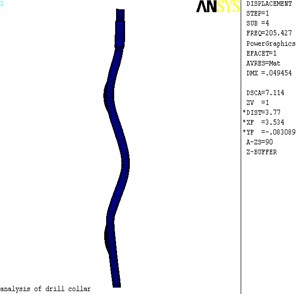
d) 4 order

Fig. 3The displacement nephogram of lateral vibration

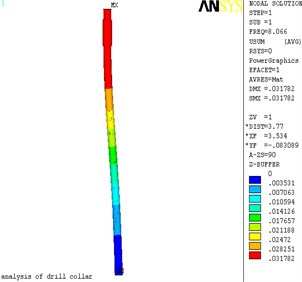
a) 1 order

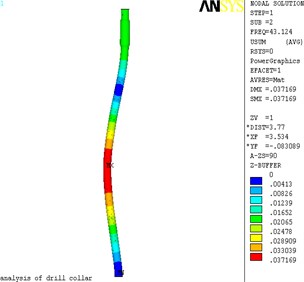
b) 2 order

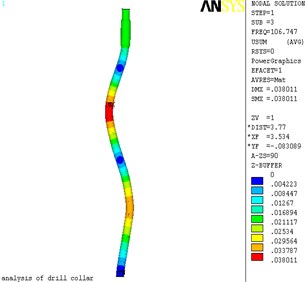
c) 3 order

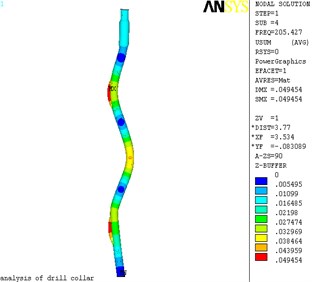
d) 4 order

The above analysis is for the case of weight on bit (WOB) of 150 kN, now applied WOB as 250 kN, simulation results show that: as the WOB increases while drilling, drillstring lateral vibration natural frequency decreases; have a certain impact to low-level (<3 orders) vibration mode, higher order (≥3 orders) vibration mode essentially unchanged.

4. Lateral vibration analysis based on the measurement data

For Rotary Steerable System (RSS) of directional drilling in the oil and gas industry, the whole drillstring is rotated from the surface by a hydraulically driven top drive (typically). It employs the use of specialized downhole equipment to replace conventional directional tools such as mud motors. The methods used to direct the well path fall into two broad categories, these being “push-the-bit” or “point-the-bit”. Push-the-bit tools (Fig. 4(a)) use pads on the outside of the tool which press against the well bore thereby causing the bit to press on the opposite side causing a direction change. The pads of the implementing agencies constantly pushed against the borehole wall, making bottom hole by a cycle of nonlinear damping force, which is lead to the bottom drilling tool movement of chaos and disorder. It is necessary for us to do in-depth research about the bottom drilling tool dynamic state of push-the-bit rotary steerable system.

High-sample-rate downhole dynamics sensors were placed at 1.5 ft above the bit in the BHA. The dynamics sensors (as shown in the Fig. 4(b)) had a sample rate of 100 Hz and consisted of an package measuring lateral, torsional, and axial vibration. The measurement system also included a magnetometer, which was used to calculate downhole drillstring rotating speed. A low-pass filter (<10 Hz) was applied to the magnetometer signal.

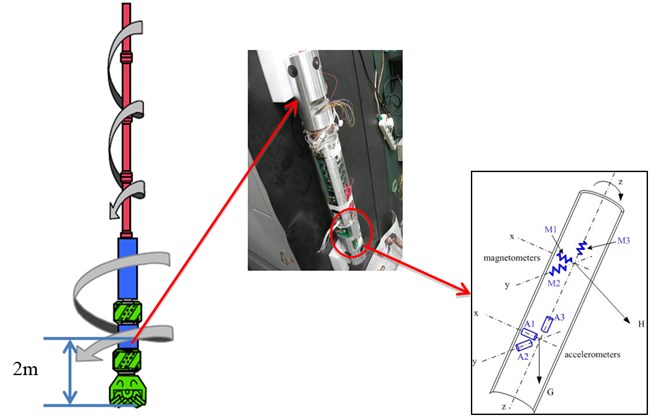
Fig. 5 shows the installing structure of the downhole measurement system developed in this paper. That is conducted by triaxial accelerometer and triaxial magnetometers, and redundancy design is adopted, more additional sensors are installed in case some of them fail.

Fig. 4a) The cross-sectional view of rotary steerable system; b) the configuration of measurement system

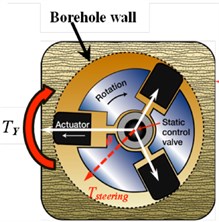
a)

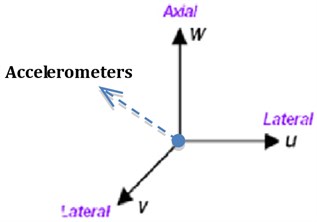
b)

Fig. 5Measurement system (Left is the simplified diagram of bottom-hole assembly; Middle is the construction of measurement system; Right is installed structure of sensors)

$a_x$, $a_y$, $a_z$ are defined as survey signals of triaxial accelerometers on the $xyz$ axis respectively. Under certain sample frequency, measuring signal is time series and can be expressed as time function. We can use:

Define the lateral vibration of the BHA and use $a_z$ express the longitudinal vibration. The survey signals of triaxial accelerometers on the $xyz$ axes as show in the Fig. 4(b) and Fig. 5.

As shown in the Fig. 6, the frequency spectrum of the measurement time series will be obtained. There is no characteristic frequencies in the $a_x$ and $a_y$ surveying signals.

We used Welch’s method [18] approach to spectral density estimation. The method is based on the concept of using periodogram spectrum estimates, which are the result of converting a signal from the time domain to the frequency domain. Welch’s method reduces noise in the estimated power spectra in exchange for reducing the frequency resolution. Due to the noise caused by imperfect and finite data, the noise reduction from Welch’s method is often desired.

The time series of lateral vibration as shown in the Fig. 7(a), frequency spectrum as shown in the Fig. 7(b). Lateral vibration violently amplitude between 0 to 10 G. Since the sampling frequency is 100 Hz, we can obtain frequency spectrum domain at 0-50 Hz, the characteristic frequency of the signal is not significant. It can be inferred that lateral vibration signals are not periodic, essentially a random vibration. The Fig. 7(c) indicate density of amplitude distributing, most of the vibration amplitude concentrated between –5G~+5G. Fig. 7(d) show the spectral density estimation using Welch’s method. The curve of power spectral density did not show significant spikes, indicating that lateral vibration can be regarded as random vibration signals at this time.

Fig. 6The spectrogram of x and y signals of accelerometer

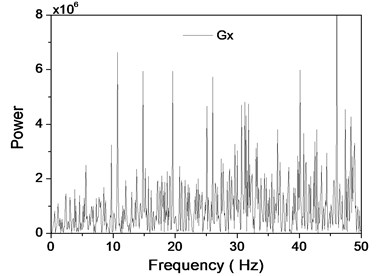
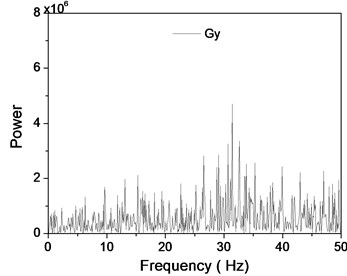
Fig. 7Time-frequency analysis of lateral vibration

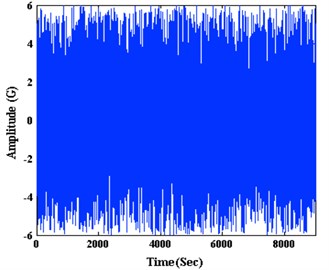
a) Time series

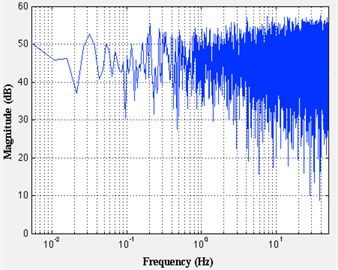
b) Frequency spectrum

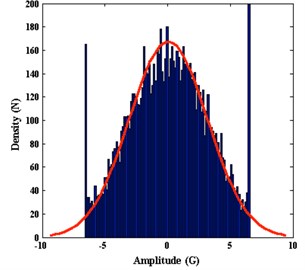
c) Density of distributing

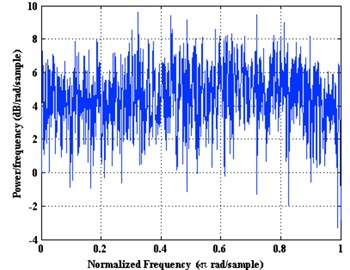
d) Periodogram spectrum estimates

Our treatment of frequency analysis would not be complete without discussing the most up-to-date methods involving dynamic spectral analysis, analyzing how the spectrum of a signal evolves in time. This analysis is carried out with Gabor transforms [19], which are close relatives of wavelet transforms. Gabor transforms are particularly useful in analyzing drillstring vibration signals. It is used to determine the sinusoidal frequency and phase content of local sections of a signal as it changes over time. The function to be transformed is first multiplied by a Gaussian function, which can be regarded as a window function, and the resulting function is then transformed with a Fourier transform to derive the time-frequency analysis.

Using the FFT algorithm, Fourier transforms for the time series of rotational speed is:

Then its power spectral density will be obtained:

We using time-frequency box to express the energy distribution of Gabor function. Time-frequency spectrum of lateral vibration signals as show in Fig. 8, the method of Gabor transform can help us discriminate the rotational movement pattern. Then Fourier transform of the $G_{u,\xi }\left(t\right)$ can be obtain:

As show in Fig. 8(a), when the drillstring does not exhibit stick-slip, the spectrum not particularly has energy concentration point, the signals can be considered as random. However, when the drillstring exhibit as stick-slip, the spectrum particularly occur energy concentration stripe, as shown in the Fig. 8(b). The results show that the stick-slip of the drillstring not only reflecting the change of the rotating speed, but also affecting the lateral vibration of the drillstring, making the drillstring lateral vibration signals lost the characteristics of random. In this case, we use largest Lyapunov exponent as observed parameters to analyze the low-dimensional chaos during the entire drilling process. The results show that the chaotic phenomenon of the drilling bit vibration exists in the whole drilling process. In field measurement data of drillstring vibration, finding chaotic characteristics is helpful to rediscover the drillstring vibration phenomenon and to improve the control algorithm of the drill string vibration in engineering [20, 21].

Fig. 8The energy spectrum of lateral vibration signals: a) non-stick-slip, b) stick-slip

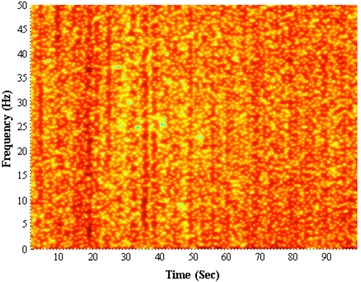
a)

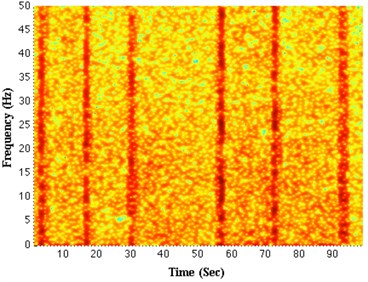
b)

5. Discussion

Drilling string vibration is a very common phenomenon that has attracted great interest of researchers. Create a more accurate theoretical model of the drillstring vibration is difficult due to the impact of complex down hole conditions, it become possibility to study the dynamic characteristics of drillstring by measuring the vibration signal with the development of measurement technology. Nowadays, the downhole-drilling tool can achieve three-dimensional vibration measurements with the development of downhole measurement technology, thus provided convincing data support for the studies of bottom drilling tool dynamics. Some even suggested that the use of the downhole vibration signals in real-time to determine formation lithology, however, these data are generally coming from some commercial companies, because the relationship of the commercial competition, many researchers cannot get the real measurement data from the field test, many studies have also only limited to the laboratory. The data in this paper collected during hundreds of hours of drilling will be a time series with massive data.

This paper obtain the natural frequencies along the drillstring of rotary steerable drilling system using the finite element model, get the deformed plot and displacement cloud map of lateral vibration as well. Additionally, develop a real-time measurement while drilling system near the drilling bit, and extract the lateral vibration time series of bottom rotating drillstring. The results of statistical analysis show that the lateral vibration can be regards as random vibration when the drillstring uniform rotating. However, when the drillstring appear stick-slip phenomenon, the energy concentration appeared in the spectrum of the lateral vibration time series, which should not be considered as random vibration any more.