Fracture toughness prediction of eutectic ceramic composite considering damage effect and transformation toughening

Ni, Xinhua; Chen, Cheng; Zhang, Shuqin

Journal of Vibroengineering

Browse Journal

Submit article

Published: 15 May 2014

Check for updates

Fracture toughness prediction of eutectic ceramic composite considering damage effect and transformation toughening

Xinhua Ni¹

Cheng Chen²

Shuqin Zhang³

^{1, 2, 3}Mechanical Engineering College, Shijiazhuang, 050003, China

Corresponding Author:

Xinhua Ni

Cite the article Download PDF

Downloads 1114

Abstract

The toughness of eutectic ceramic composites is obtained by multiple toughening mechanisms involving crack-bridging and pull-out of rod-shaped eutectics, as well as stress-induced transformation toughening. In the loading procedure, damage will emerge in the rod-shaped eutectic. Firstly, the damage variables are defined by the microstructure of rod-shaped eutectic with aligned nano/micro- fibers. The maximum strain criterion is used for determining the loading function. According to the attenuation characteristic of eutectic rigidity, the critical fracture stress of the damage rod-shaped eutectic is obtained by damage variable maximizing. Secondly, we imagine the bridging load carried by the damage rod-shaped eutectics in the crack wake to produce a crack-closing force. The latter reduces the stress intensity in front of the crack. The pull-out work is given by the integral of the frictional force over the pull-out length. Bridging toughening mechanism and pull-out toughening mechanism of damage rod-shaped eutectics are constructed. Thirdly, defining a parabola transformation yield function, the transformation plastic strain increment is gotten by transformation plastic potential function. The screening impact of transformation particles for mixed-mode I-II crack is gained. And lastly, based on the crack-bridging and pull-out of rod-shaped eutectics, as well as stress-induced transformation toughening mechanisms, the added toughness scale with the inherent matrix toughness, the theoretical formula of fracture toughness of the eutectic ceramics composite is determined. The result shows that the fracture toughness is dependent on the aspect ratio of rod-shaped eutectic: the fracture toughness is minimum as the aspect ratio is equal to 0.3 and maximizing when the aspect ratio is equal to 14. The damages inside eutectics enlarge the incremental range of variation of the fracture toughness. The transformation particles exert a slight influence on the fracture toughness due to its less content.

1. Introduction

In various industrial fields, there is a great need for materials having high strength combined with high toughness. Directionally solidified eutectics contain a large amount of clean interfaces between two strongly-bonded phases with typical inter-phase spacing in the micron range, and these characteristics result in an improvement of some material properties. For instance, rods of oxide/oxide eutectics present a smooth surface and exhibit high strength and toughness, chemical stability in oxidizing environments as well as excellent thermal shock resistance [1]. The increase of the hardness or strength of the ceramics could be attributed to nano-submicron interphase spacing and the refinement of the eutectic grains, whereas high-energy, high-angle boundaries between rod-shaped grains could also introduce strong toughening mechanisms involving crack-bridging and pull-out of rod-shaped grains[2]. Experiments showed that there were two kinds of fracture models – fracture in the rod-shaped eutectics and fracture in inter-eutectics regions. Because of the presence of nano-submicrometer t-ZrO₂ fibers and inter-phase spacing in the colony as well as micrometer t-ZrO₂ spherical grains in the inter-colony region, intensive coupled toughening of residual stress toughening, transformation toughening and transformation-induced microcrack toughening mechanisms was bound to occur [3].

It has been widely recognized that one of the most significant barriers to the increased use of composite materials is inability to predict accurately mechanical properties. The mechanical properties prediction of oxide/oxide eutectic composite is particularly challenging when there were two kinds of fracture models – fracture in the rod-shaped eutectics and fracture in inter-eutectics regions.

The fracture model in inter-eutectics regions is used to predict the strength of oxide/oxide eutectic composited by the maximum stress of matrix equalling to theoretical strength [4] and obtain the bridging toughening mechanism by the micro boundary sliding [5]. Generally, fracture model alone are unable to predict the mechanical properties of oxide/oxide eutectic composite. To predict failure initiation, propagation and final fracture, it is necessary to combine the fracture model in the rod-shaped eutectics with appropriate damage model.

To overcome some of the difficulties in the consideration of the interaction between fracture mechanisms, the objective of this work is to determine the breaking stress of the rod-shaped eutectic and the fracture thenghness of composite creamic by the damage evolution in the rod-shaped eutectic.

2. The breaking stress of the damage eutectic

Composites mainly compose of randomly-oriented rod-shaped eutectic grains, within the rod-shaped grains, aligned nano-micron fibers are embedded. Overlooking the resistance of crystal lattice against dislocation motion, the micro strength formation of rod-shaped eutectics is computed by the dislocation pileup theory [4]:

1

σ_{f u} = \frac{2 E_{22}}{n (A E_{22} + E_{b} υ_{21}) t a n h (n l / d)} \sqrt{\frac{3 E_{0} γ_{0}}{2 d}},

where, $E_{22}$ is the longitudinal (which is perpendicular to the axial direction of fiber) elastic modulus of the eutectic [6], $E_{0}$ the elastic modulus of matrix, $γ_{0}$ free surface energy of matrix, $E_{b}$ the elastic modulus of fibers. $υ_{21} = 1 - E_{22} / 2 μ_{12}$ , and $μ_{12}$ is the longitudinal shear modulus of eutectic [6]. $l$ and $d$ are length and diameter of fiber. Parameters $A$ and $n$ are given as follow:

A = \frac{Γ}{2 (1 + Γ - 2 υ_{12})} [\frac{(1 + Γ) (1 - υ) (1 + υ_{12})}{(1 + υ)} - (1 + Γ + υ_{12} Γ - 3 υ_{12})],

n^{2} = \frac{1}{(1 + υ_{12}) Γ l n (\frac{π}{f_{b}})} .

Here, $Γ = μ_{12} / μ$ , $μ$ is shear modulus of composite [6], $υ$ the Poisson’s ratio of composite [6], $l$ and $d$ are length and diameter of fiber. The fracture strength of eutectics is determined by Eq. (1) which is based on the assumption that the maximum stress equals to the theoretical strength of matrix. In fact, eutectic fracture is the damage accumulation process, so the damage model needs to be built.

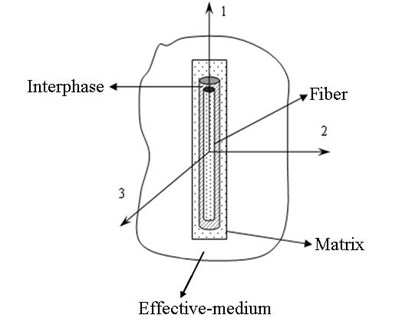
Our study is based on the four-phase model [6] in which a fiber with an interphase is embedded in a finite matrix that is wrapped in an infinite elastic medium, as shown in Fig. 1. Consider a vector $e_{1} = {1, 0, 0}^{T}$ , parallel to the fiber direction. In the transversely isotropic plane, orthogonal to $e_{1}$ , there is a set of orthogonal vectors ${e_{2}, e_{3}}$ that define a plane where the shear strain is zero.

Assuming a constant density, the total complementary free energy is given as $\int_{V} ψ d V$ , where $ψ$ is the complementary free energy per unit volume. The proposed definition for the complementary free energy per unit volume is:

2

\begin{matrix} ψ = \frac{σ_{11}^{2}}{2 (1 - d_{1}) E_{11}} + \frac{1}{2 E_{22}} (\frac{σ_{22}^{2}}{1 - d_{2}} + \frac{σ_{33}^{2}}{1 - d_{3}}) - \frac{υ_{12}}{E_{11}} (σ_{22}^{} + σ_{33}^{}) σ_{11}^{} \\ - \frac{υ_{23}}{E_{22}} σ_{22}^{} σ_{33}^{} + \frac{σ_{12}^{2} + σ_{13}^{2}}{2 (1 - d_{6}) G_{12}} + [α_{11} σ_{11} + α_{22} (σ_{22}^{} + σ_{33}^{})] Δ T, \end{matrix}

where, $E_{11}$ is the elastic modulus that is parallel to the fiber direction [6]. $α_{11}$ and $α_{22}$ are the coefficients of thermal expansion in the longitudinal and transverse direction respectively [7]. $Δ T$ is temperature difference. The damage variable $d_{1}$ represents micro-cracks parallel to the longitudinal of eutectic. The damage variable $d_{2}$ represents micro-cracks parallel to the fiber direction, whereas $d_{3}$ represents micro-cracks normal to the fiber direction and the longitudinal of eutectic. The damage variable $d_{6}$ affects the shear module.

Fig. 1The four-phase model of eutectic

From Eq. (2), the compliance tensor is defined as:

3

S^{'} = \{\begin{matrix} S_{11}^{'} & 0 \\ 0 & S_{22}^{'} \end{matrix}\} .

Here:

S_{11}^{'} = [\begin{matrix} \frac{1}{(1 - d_{1}) E_{11}} & - \frac{υ_{12}}{E_{22}} & - \frac{υ_{12}}{E_{22}} \\ - \frac{υ_{12}}{E_{11}} & \frac{1}{(1 - d_{2}) E_{22}} & - \frac{υ_{12}}{E_{22}} \\ - \frac{υ_{12}}{E_{11}} & - \frac{υ_{23}}{E_{22}} & \frac{1}{(1 - d_{3}) E_{22}} \end{matrix}],

S_{22}^{'} = [\begin{matrix} \frac{1}{(1 - d_{6}) μ_{12}} & 0 & 0 \\ 0 & \frac{1}{(1 - d_{6}) μ_{12}} & 0 \\ 0 & 0 & \frac{1}{μ_{23}^{'}} \end{matrix}],

υ_{23} = \frac{E_{22}}{2 μ_{23}} - 1 .

$μ_{23}^{'}$ is the transverse shear modulus of eutectic. $d_{1}$ , $d_{2}$ and $d_{3}$ are the damage variables in the direction defined by the vectors ${e_{1}, e_{2}, e_{3}}$ . These damage variables depend on the tensional ( $d_{T +}$ ) and compressional ( $d_{T -}$ ) damage variables as:

4

\begin{matrix} d_{1} = d_{T +}^{1} \frac{〈 σ_{11} 〉}{| σ_{11} |} + d_{T -}^{1} \frac{〈 - σ_{11} 〉}{| σ_{11} |}, \\ d_{2} = d_{T +}^{2} \frac{〈 σ_{22} 〉}{| σ_{22} |} + d_{T -}^{2} \frac{〈 - σ_{22} 〉}{| σ_{22} |} \\ d_{3} = d_{T +}^{3} \frac{〈 σ_{33} 〉}{| σ_{33} |} + d_{T -}^{3} \frac{〈 - σ_{33} 〉}{| σ_{33} |}, \end{matrix},

where $〈 x 〉$ is the McCauley operator defined as: $〈 x 〉 = (x + | x |) / 2$ .

Owing to micro heterogeneous plasticity in the eutectic, the micro-cracks paralleled to the fiber direction will nucleate where is nearer the interface [4]. The damage variables paralleled to the longitudinal of eutectic is not able to detect the directionality of micro-cracks, i.e.:

5

d_{T +}^{1} = d_{T -}^{1} = 0, or d_{1} = 0 .

The damage variables related to the micro-cracks paralleled to the fiber direction change when the normal stress switch from positive to negative or vice-versa. When this normal stress is negative, these micro-cracks do not propagate, so $d_{T -}^{2}$ vanishes. It should be noted that the closure effect in the transversely isotropic plane is activated independently in the direction $e_{2}$ and $e_{3}$ . If the stresses in the transversely isotropic plane have the same sign, the damage variables have the same value ( $d_{2} = d_{3}$ ), thus:

6

d_{2} = d_{3} = d_{T +}^{2} \frac{〈 σ_{22} 〉}{| σ_{22} |} = d_{T +}^{2} .

The coaxially of stresses and strains in the transversely isotropic plane is enforced and the correspondent shear modulus is evaluated as:

7

μ_{23}^{'} = \frac{σ_{33} - σ_{22}}{2 (ε_{33} - ε_{22})} .

From Eq. (6), we know that the damage variables have the same value in the transversely isotropic plane, so the shear modulus is transformed as:

8

μ_{23}^{'} = \frac{E_{22}}{2 [1 + υ_{23} (1 - d_{2})]} .

Fig. 2Arrangement of fibers in eutectic

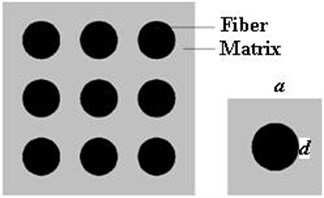
The eutectic is made up of many square cylinder cells and each cell includes a fiber. These cells are evenly arranged in the same direction, as shown in Fig. 2. Assuming the side length of the square is $a$ , the cylinder length is $l$ . The fraction $f_{b}$ of aligned fibers can be expressed as:

9

f_{b} = \frac{π d^{2} l}{4 a^{2} l} = \frac{π d^{2}}{4 a^{2}} .

Obviously, the maximum cracking region is the half circular column between fiber and matrix. Thus, the minimum area of damage region in a cell can be expressed as $A_{m i n} = (a - d) l$ . The corresponding maximum damage variable is satisfied as:

10

d_{2 m a x} = 1 - \frac{A_{m i n}}{A} = 1 - \frac{(a - d) l}{a l} = \frac{d}{a} = \sqrt{\frac{4 f_{b}}{π}} .

The change limit of damage variable $d_{2}$ is $0 \leq d_{2} \leq \sqrt{4 f_{b} / π}$ . The shear damage variable is not influenced by the normal stress, i.e.:

11

d_{6} = 0 .

Substitute Eqs. (5), (6), (8) and (11) into Eq. (3) the compliance tensor of damage eutectic can be obtained.

In the loading procedure, the damage variables paralleled to the longitudinal of eutectic can be neglected, so the elastic modulus parallel to the fiber direction does not change. The shear damage variable is not influenced by the sign of the shear stress components and the normal stress that produce friction between the micro-crack allowing transfer and dissipation, thus, the shear modulus does not change too. When this normal stress along $e_{2}$ directionis compressible, these micro-cracks do not grow. So $d_{L -} = 0$ . Owing the damage in the transversely isotropic plane, the longitudinal elastic modulus of the eutectic will decay.

When damage variable attains maximum, the transverse and longitudinal elastic module of eutectics are:

12

{E_{11}^{'} = E_{11}, E}_{22}^{'} = (1 - \sqrt{\frac{4 f_{b}}{π}}) E_{22} .

The eutectic is suffered from the tension stress $σ$ along with coordinated axis $e_{2},$ i.e. $σ_{11} = σ_{33} =$ 0, $σ_{22} = σ$ . In matrix, the strain along the longitudinal direction of the eutectic is the main factor that causes local damage [8]. The maximum strain can be expressed as:

13

ε_{m a x} = ε_{2} .

The maximum strain criterion is used for loading function:

14

ϕ = \frac{E_{c}}{X_{T}} 〈ε_{c}〉 .

Here, $E_{c}$ is the elastic modulus along the $ε_{c}$ , and $X_{T} = 1 - d_{2}$ . The longitudinal failure of unidirectional eutectic under tensional stress is a far more complex phenomenon. The tensional failure is the result of a complex sequence of damage mechanisms. On basis of Eqs. (13) and (14), we know:

15

ϕ = \frac{E_{22}}{X_{T}} 〈ε_{22}〉 = \frac{E_{22}}{1 - d_{2}} 〈ε_{22}〉 .

Owing to $ε_{22} = \frac{σ}{(1 - d_{2}) E_{22}} > 0$ , so:

16

〈ε_{22}〉 = ε_{22} = \frac{σ}{(1 - d_{2}) E_{22}} .

Substituting Eq. (16) into Eq. (15), we have:

17

ϕ = \frac{σ}{{(1 - d_{2})}^{2}} .

When the rod-shaped eutectic is undamaged, the loading function equals to $σ_{f u}$ . Substituting Eq. (1) into Eq. (17), as damage variable attains maximum, the breaking stress of the damage eutectic is:

18

σ_{d u} = \frac{2 {E^{'}}_{22}}{n (A {E^{'}}_{22} + E_{b} υ_{21}) t a n h (n l / d)} {(1 - d_{2})}^{2} \sqrt{\frac{3 E_{0} γ_{0}}{2 d}} .

The breaking stress of the damage eutectic depends on the fraction, shape and diameter of fiber, and on the elastic modulus and free surface energy of matrix.

3. Damage eutectic toughening

Composite ceramic is mainly constructed by the rod-shaped eutectic with parallel nano/micro-fibers, and a small amount of matrix particles and transformation particles are distributed in the fiber eutectic around. In the loading procedure, damage will emerge in the rod-shaped eutectic. Suppose composite ceramic with cracks, loaded, the crack is limited by the damage rod-shaped eutectic in the crack surface. At the crack surface, the bridging stress is [5]:

19

σ_{f} (L_{s}) = \frac{σ_{f}}{2} (\sqrt{1 + \frac{16 E_{22}^{'} τ u}{R σ_{f}^{2} s i n α}} + 1),

where, $σ_{f}$ is the load undertaken by damage rod-shaped eutectic at far distance from crack, $R$ is the radius of the damage rod-shaped eutectic, $τ$ is the shear stress on the sliding part of the damage rod-shaped eutectic, $u$ is the crack opening displacement. $α$ is the angle between the bridging damage eutectic and crack. While the crack opening is limited by the damage rod-shaped eutectic, some debonding of the damage rod-shaped eutectic takes place. The toughening can be discussed in two ways. In one, the load carried by the rod-shaped eutectic in the crack wake to produce a crack-closing force. This force reduces the stress intensity in front of the crack. Further, because of residual thermal stress, a frictional stress exists across some rod-shaped eutectic. The frictional work of damage eutectic pull-out adds to the material toughness.

The bridging force of the damage rod-shaped eutectic on the crack surface makes cracks arise closure effect, reducing the crack-tip stress concentration. When the crack propagation direction and the longitudinal of damage rod-shaped eutectic are not inconsistent, the crack tip would be continue to expand bypass the damage rod-shaped eutectic. Its elastic strain will be released to consume mechanical energy required to crack propagation. Thereby, it can prevent the further expansion of cracks, induce the crack bridging toughening mechanism.

Consider the orientation and fraction of the damage rod-shaped eutectic. The bridging load can be determined by Eq. (20):

20

T = f_{f} σ_{f} (L_{s}) s i n α = \frac{f_{f} σ_{f} s i n α}{2} (\sqrt{1 + \frac{16 E_{22}^{'} τ u}{R σ_{f}^{2} s i n α}} + 1) .

Here, $f_{f}$ is the fraction of the damage rod-shaped eutectic. The energy dissipation in the process of bridging $Δ J_{1}$ is the function of the bridging load $T$ and the opening displacement $u$ , i.e. $Δ J_{1} = \int_{0}^{u_{m a x}} T d u .$ Suppose that the direction of the damage rod-shaped eutectic is three-dimensional position of completely random distribution. The energy dissipation can be calculated as follow [5]:

21

Δ J_{1} = \frac{χ f_{f} R σ_{d u}^{3}}{E τ} .

Here, $E$ is the elastic modulus of the composite ceramic. The constant $χ$ is determined by $E_{22}^{'}$ and $E$ [5]. According to the point of the energy dissipation, the relationship of break tenacity and energy dissipation is $Δ K_{C} = {(E Δ J)}^{1 / 2}$ . We take aspect ratio $λ = L / (2 R)$ , the bridging toughening value of the damage rod-shaped eutectic is:

22

Δ K_{C 1} = \sqrt{\frac{χ f_{f} L σ_{d u}^{3}}{2 λ τ}} .

Eq. (22) shows that the damage of rod-shaped eutectic decreases the bridging toughening value by decreasing the breaking strength $σ_{d u}$ .

Fractured ceramic often exhibit some structural integrity. That is, failed samples often remain intact and can be completely separated only by application of a post-fracture stress. It is as if there were contacting ligaments between the halves of the fractured sample. The irregular crack path implies that some eutectics to each side of the main crack protrude into the other side. When thermal residual stresses are present, this eutectic pull-out work can be appreciable. The residual stresses are manifested by a clamping force between eutectic and particles that overcome in accomplishing their final separation. The work done in this separation represents additional fracture work.

The additional fracture work can be calculated on the basis of it arising from a frictional clamping force. The pull-out work is given by the integral of the frictional force over the pull-out length, $l$ . The length $l$ is the instantaneous distance over which the eutectic is clamped, and varies with the extent of pull-out. It initially has the value $l_{0}$ and $0 < l_{0} < L / 2$ , the area over which the frictional force operates is:

23

S = 2 π R (L - l_{0}) .

But the pull-out length decreases with the pull-out distance $x$ , as $l = L - l_{0} - x$ . The frictional stress is $τ = μ σ_{n}$ where $μ$ is the coefficient of friction and $σ_{n}$ the gripping pressure, here reasonably taken as the residual compressive stress [9]. Thus, the pull-out work is given by:

24

W = τ \int_{0}^{L_{0}} [2 π R (L - l_{0} - x)] d x .

Dividing Eq. (24) by $d S = π R^{2} / 4$ (the acrossal area of the pulled-out eutectic) yields the fracture work per unit area. This can be equated to $Δ J$ . However, only a fraction $f_{f}$ of eutectics is subject to crack bridging. Thus, the pull-out work per unit area is:

25

Δ J_{2} = f_{f} μ σ_{n} \int_{0}^{L_{0}} \frac{L - L_{0} - x}{2 R} d x,

i.e.

26

Δ J_{2} = f_{f} μ σ_{n} \frac{L_{0} (2 L - 3 L_{0})}{4 R} .

The maximum pull-out distance would be $L / 2$ , the minimum would be zero. We take the average distance as $L / 4$ , then, $L_{0}$ can be replaced by $L / 4$ . The pull-out work per unit area is transformed as:

27

Δ J_{2} = \frac{5 f_{f} μ σ_{n} L^{2}}{64 R} .

According to Eq. (27), maximum pull-out work per unit area is obtained by increasing the fraction and length of rod-shaped eutectics, as well as the friction coefficient of interface and residual compressive stress, reducing eutectic radius.

Analysis of the added toughness proceeds along lines used in analyzing bridging toughening. We use $Δ K_{C} = {(E Δ J)}^{1 / 2}$ and $λ = L / (2 R) .$ The pull-out toughening value of the damage rod-shaped eutectic can be expressed as:

28

Δ K_{C 2} = \sqrt{\frac{5 f_{f} μ σ_{n} E_{22}^{'} λ L}{32}} .

Note that there is an implicit damage effect in Eq. (28). The elastic modulus $E_{22}^{'}$ varies inversely with damage variable. Thus, provided we are in the damage variable domain where pull-out toughening exists, the toughening is smaller for composite ceramic with the damage rod-shaped eutectic.

4. Transformation toughening

In the ceramic composite containing damage eutectics and transformation particles, the transformation may be triggered by the stress field associated with a crack. As the crack advances, tetragonal particles transform to the monoclinic form in a zone above and below the fracture plane. The work expended in effecting this transformation adds to the material toughness.

For the transformation toughening, the comprehensive transformation criterion [10] was used to describe the plastic behavior of partially stabilized zirconias. The transformation yield condition was defined by the macro equivalent stress and average stress. For the tectic ceramic composite, there are rod-shaped eutectics around transformation particles, so the transformation yield condition is not only related to the macro equivalent and average stresses, but also the difference between the maximum tensile stress and compressive stress. Based on the experiment, the parabola transformation yield function is defined as follow:

29

F = a σ_{0} + J_{2} - k^{2} = 0,

where, $a = (σ_{1} - σ_{3}) / 3$ , $σ_{1}$ is the maximum tensile stress and $σ_{3}$ the maximum compressive stress determined by the stress field associated with a crack. $σ_{0}$ is the bulk stress, i.e. $σ_{0} = σ_{1} + σ_{2} + σ_{3}$ . $k$ is material constant. $J_{2}$ is the second stress invariant, i.e. $J_{2} = S_{i j} S_{i j} / 2$ , and $S_{i j} = σ_{i j} - \frac{1}{3} σ_{0} δ_{i j}$ , the stress deviator tensor.

According to potential function method, the gradient of plastic strain tensor is gotten from Eq. (29):

30

d ε_{i j}^{p} = d λ \frac{\partial F}{\partial σ_{i j}} = d λ (a δ_{i j} + S_{i j}) .

In the general case of material fracture, the stress field is associated with a crack involves I-II combination:

31

\{\begin{array}{l} σ_{x} = \frac{K_{I}}{\sqrt{2 π r}} c o s \frac{θ}{2} [1 - s i n \frac{θ}{2} s i n \frac{3 θ}{2}] - \frac{K_{II}}{\sqrt{2 π r}} s i n \frac{θ}{2} [2 + c o s \frac{θ}{2} c o s \frac{3 θ}{2}], \\ σ_{y} = \frac{K_{I}}{\sqrt{2 π r}} c o s \frac{θ}{2} [1 + s i n \frac{θ}{2} s i n \frac{3 θ}{2}] + \frac{K_{II}}{\sqrt{2 π r}} c o s \frac{θ}{2} s i n \frac{θ}{2} c o s \frac{3 θ}{2}, \\ τ_{x y} = \frac{K_{I}}{\sqrt{2 π r}} c o s \frac{θ}{2} s i n \frac{θ}{2} c o s \frac{3 θ}{2} + \frac{K_{II}}{\sqrt{2 π r}} c o s \frac{θ}{2} [1 - s i n \frac{θ}{2} s i n \frac{3 θ}{2}], \\ σ_{z} = υ (σ_{x} + σ_{y}) . \end{array}

Substituting Eq. (31) into Eq. (29), we can obtain the radius of transformation region of stationary crack:

32

r = {(\frac{K_{I}}{a})}^{2} \frac{e^{2}}{2 π [2 {(1 + υ)}^{2} g^{2} + b^{2} e - 2 (1 + υ) g \sqrt{{(1 + υ)}^{2} g^{2} + b^{2} e}]},

where:

b = \frac{k}{a}, e = e_{1} + α e_{2} + α^{2} e_{3}, α = \frac{K_{I I}}{K_{I}}, g = c o s \frac{θ}{2} - α s i n \frac{θ}{2},

e_{1} = \frac{1}{3} (4 υ^{2} - 4 υ + 1) {c o s}^{2} \frac{θ}{2} + \frac{1}{4} {s i n}^{2} θ, e_{2} = \frac{1}{3} (- 4 υ^{2} + 4 υ - 1) s i n θ + \frac{1}{2} s i n 2 θ,

e_{3} = \frac{1}{3} (4 υ^{2} - 4 υ + 1) {s i n}^{2} \frac{θ}{2} - \frac{3}{4} {s i n}^{2} θ + 1 .

As the crack advances, tetragonal particles transform to the monoclinic form in a zone lying $\pm H$ above and below the fracture plane. The $H$ can be determined for Eq. (32). Let $d (r s i n θ) / d θ = 0$ , we get $θ = θ_{m}$ . Then $H = {(r s i n θ)}_{θ = θ_{m}}$ . The radius of transformation region of steady-state growing crack is given:

33

r = \{\begin{array}{l} {(\frac{K_{I}}{a})}^{2} \frac{e^{2}}{2 π [2 g^{2} + b^{2} e - 2 g \sqrt{g^{2} + b^{2} e}]}, & 0 \leq θ \leq θ_{m}, \\ \frac{H}{s i n θ}, & θ_{m} \leq θ \leq π . \end{array}

On base of weighted function, the transformation fracture enhancements of mode I and mode II are calculated as follow [11, 12]:

34

d K_{I} = \int_{s} {\vec{h}}_{I} (s, c) \vec{T} (s) d s,

35

d K_{II} = \int_{s} {\vec{h}}_{I I} (s, c) \vec{T} (s) d s .

Here $s$ is the boundary of transformation region. $c$ is the length of crack. ${\vec{h}}_{I} (s, c)$ and ${\vec{h}}_{I I} (s, c)$ are the weight functions of mode I and II respectively. The components of surface force $\vec{T} (s)$ on the boundary are expressible in the form:

36

T_{i} = \frac{E}{3 (1 - 2 υ)} ε_{k k}^{p} δ_{i j} n_{j} + \frac{E}{1 + υ} e_{i j}^{p} n_{j},

where $n_{j}$ is the direction consine. The plastic strain tensor are gotten:

37

\{\begin{array}{l} ε_{k k}^{p} = f_{t} ε_{k k}^{T}, \\ e_{i j}^{p} = \frac{f_{t} ε_{k k}^{T} S_{i j}}{3 a} . \end{array}

In equation $ε_{k k}^{T}$ is the corresponding martensite transformation strain, $f_{t}$ is the fraction of the triclinic phase in the distance $\pm H$ above and below the fracture plane that transforms martensitically.

We can acquire the weight function of mode I [11]:

38

{\vec{h}}_{I} = \frac{1}{2 (1 - υ) \sqrt{2 π r}} \{\begin{matrix} c o s \frac{θ}{2} (2 υ - 1 + s i n \frac{θ}{2} s i n \frac{3 θ}{2}) \\ s i n \frac{θ}{2} (2 - 2 υ - c o s \frac{θ}{2} c o s \frac{3 θ}{2}) \end{matrix}\} .

The weight function of mode II is [12]:

39

{\vec{h}}_{I I} = \frac{1}{2 (1 - υ) \sqrt{2 π r}} \{\begin{matrix} s i n \frac{θ}{2} (2 - 2 υ + c o s \frac{θ}{2} c o s \frac{3 θ}{2}) \\ c o s \frac{θ}{2} (1 - 2 υ + s i n \frac{θ}{2} s i n \frac{3 θ}{2}) \end{matrix}\} .

Substituting Eqs. (36) and (38) into Eq. (34), we have:

40

Δ K_{I} = \frac{f_{t} E ε_{k k}^{T}}{6 (1 - υ) \sqrt{2 π}} \iint_{A} \{r^{- \frac{3}{2}} c o s \frac{3 θ}{2} + (\frac{K_{I I}}{a}) \frac{r^{- 2}}{3 (1 + υ) \sqrt{2 π}} (e_{11} + e_{12})\} d A .

Here:

e_{11} = - \frac{9}{4} c o s θ + (8 υ^{2} - 3 υ - 2) {c o s}^{2} θ + (2 υ^{2} - \frac{3}{2} υ + \frac{13}{4}) c o s θ + \frac{3}{2} v + 1,

e_{12} = \frac{K_{II}}{K_{I}} [\frac{27}{4} {c o s}^{3} θ - (8 υ^{2} - 3 υ - 2) {c o s}^{2} θ + (2 υ^{2} - \frac{5}{2} υ - \frac{15}{4}) c o s θ + 4 υ^{2} - \frac{3}{2} υ - 1],

where, $A$ is the area of transformation region.

Substituting Eqs. (36) and (39) into Eq. (35), we obtain:

41

Δ K_{I I} = \frac{f_{t} E ε_{k k}^{T}}{6 (1 - υ) \sqrt{2 π}} \iint_{A} \{r^{- \frac{3}{2}} s i n \frac{3 θ}{2} + (\frac{K_{I I}}{a}) \frac{r^{- 2}}{3 (1 + υ) \sqrt{2 π}} (e_{21} + e_{22})\} d A,

where:

e_{21} = [\frac{9}{4} {c o s}^{2} θ - (8 υ^{2} - 3 υ - 2) c o s θ - 2 υ^{2} + 2 υ - \frac{5}{4}] s i n θ,

e_{22} = \frac{{\bar{K}}_{II}}{{\bar{K}}_{I}} [\frac{27}{4} {c o s}^{3} θ - (8 υ^{2} - 3 υ - 2) {c o s}^{2} θ + (2 υ^{2} - \frac{5}{2} υ - \frac{15}{4}) c o s θ + 4 υ^{2} - \frac{3}{2} υ - 1] .

For the giving $K_{II} / K_{I}$ and $k / a$ , Eq. (40) is integrated in the transformation region of steady-state growing crack given by Eq. (33). We gain to the toughening effects of mode I crack:

42

Δ K_{I} = Δ_{1} f_{t} E ε_{k k}^{T} \sqrt{H} .

On integrating Eq. (41) in the transformation region of steady-state growing crack given by Eq. (33) the transformation region, we get the toughening effects of mode II crack:

43

Δ K_{I I} = Δ_{2} f_{t} E ε_{k k}^{T} \sqrt{H} .

Here $Δ_{1}$ and $Δ_{2}$ are constants relating to $υ$ , $K_{II} / K_{I}$ and $k / a$ . For mixed-mode I-II crack, using the strain energy release rate criterion, we obtain the fracture enhancement of transformation:

44

Δ K = \frac{Δ K_{I} + (K_{II} / K_{I}) Δ K_{II}}{\sqrt{1 + {(K_{II} / K_{I})}^{2}}} .

Substituting Eqs. (42) and (43) into Eq. (44), the expression for the transformation-effected toughness can be written as:

45

Δ K_{C 3} = Δ f_{t} E ε_{k k}^{T} \sqrt{H} .

In Eq. (22), $∆_{1}$ is a constant relating to $υ$ , $K_{II} / K_{I}$ and $k / a$ . For Al₂O₃-ZrO₂ ceramic composite containing damage Eutectics and transformation Particles, $υ = 0.31$ , $K_{II} / K_{I} =$ 0.5, $k / a =$ 2.5. We can determine $∆ =$ 0.0732, i.e.:

46

Δ K_{C 3} = 0.0732 f_{t} E ε_{k k}^{T} \sqrt{H} .

The transformation toughening is associated with the fraction of the transformation particles, the elastic modulus of composite ceramic and the half width of transformation region. Under the unidirectional tension load, the half width of transformation region can be determined by $H = 4.3 {(2 K_{m} / σ_{c})}^{2}$ . Here, $K_{m}$ is the inherent matrix toughness, and $σ_{c}$ is the stress initiating the martensite transformation.

5. Fracture toughness of ceramic composite

Experiments showed that there were two kinds of fracture models – fracture in the rod-shaped eutectics and fracture in inter-eutectics regions. Because of presence of nano-submicrometer fibers and inter-phase spacing in the eutectic as well as micrometer transformation particles in the inter-eutectic region, intensive coupled toughening of damage eutectic-induced crack bridging toughening, eutectic pull-out toughening and transformation toughening. For the coupled toughening mechanisms discussed above, the added toughness scales with the inherent matrix toughness (i.e. $K_{m}$ ). Thus, the fracture toughness $K_{C}$ of ceramic composite is:

47

K_{C} = K_{m} + Δ K_{C 1} + Δ K_{C 2} + Δ K_{C 3} .

$Δ K_{C 1}$ , $Δ K_{C 2}$ and $Δ K_{C 3}$ can be given by Eqs. (22), (28) and (48) respectively. According to Eq. (22) and (28), we can make out that the bridging toughening value and pull-out toughening value have a bearing on the aspect ratio of damage eutectics which are main structure of the ceramic composite. Thus, we analyse the relation between the fracture toughness of the ceramic composite and the aspect ratio of damage eutectics quantitatively as follow. For the ceramic composite mainly constructed by Al₂O₃/ZrO₂ eutectics, the fraction $f_{f}$ of the damage rod-shaped eutectic equals to 0.9, the friction coefficient between eutectics and particles is 0.2, eutectic length is 200 μm, the fraction $f_{t}$ of the triclinic phase is 0.04, martensite transformation strain is 1.05, the inherent matrix toughness is 4.5 MPa·m^1/2, the stress initiating the martensite transformation is 900 MPa. To discuss the effect of transformation particles on the fracture toughness, we analyse quantitatively the fracture toughness under two circumstances of $Δ K_{C 3}$ vanishing and calculated by Eq. (48). The description of the toughness-aspect ratio relation under two circumstances is provided in the schematic Fig. 3.

Fig. 3Schematic illustrates the variation of the fracture toughness with eutectic aspect ratio and the effect of transformation particles on the fracture toughness

$Schematic illustrates the variation of the fracture toughness with eutectic aspect ratio and the effect of transformation particles on the fracture toughness$

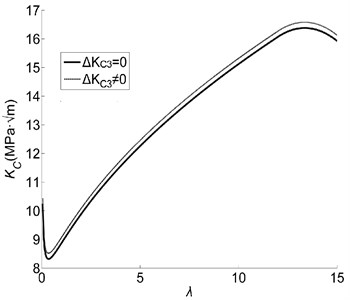
As shown in Fig. 3, the fracture toughness is dependent on the aspect ratio of damage rod-shaped eutectic: the fracture toughness is minimum as the aspect ratio is equal to 0.3 and maximizing when the aspect ratio is equal to 14. Comparing the fracture toughness of the composite with damage to that with no damage [5], the damages inside eutectics enlarge the incremental range of variation of the fracture toughness. The transformation particles exert a slight influence on the fracture toughness due to its content is less.

6. Conclusions

1) The damage variables are defined by the microstructure of rod-shaped eutectic with parallel nano/micro-fibers. The maximum strain criterion is used for determining the loading function. According to the attenuation characteristic of eutectic rigidity, the critical fracture stress of the damage rod-shaped eutectic is obtained by damage variable maximizing.

2) Bridging toughening mechanism and pull-out toughening mechanism of damage rod-shaped eutectics are constructed. The damage of rod-shaped eutectic decreases the bridging toughening value and pull-out toughening value.

3) Defining a parabola transformation yield function, the transformation plastic strain increment is gotten by transformation plastic potential function. The screening impact of transformation particles for mixed-mode I-II crack is gained.

4) Based on the crack-bridging and pull-out toughening mechanisms of damage rod-shaped eutectics, as well as stress-induced transformation toughening mechanism, the added toughness scale with the inherent matrix toughness, the theoretical formula of fracture toughness of the eutectic ceramics composite are determined. The result shows that the fracture toughness is dependent on the aspect ratio of rod-shaped eutectic: the fracture toughness is minimum as the aspect ratio is equal to 0.3 and maximizing when the aspect ratio is equal to 14. The damages inside eutectics enlarge the incremental range of variation of the fracture toughness. The transformation particles exert a slight influence on the fracture toughness due to its content is less.

References

Lorca J., Orera V. M. Directionally solidified eutectic ceramic oxides. Progress in Materials Science, Vol. 51, 2006, p. 711.

Search CrossRef
Zhao Z. M., Zhang L., Song Y. G., Wang W. G., Wu J. Microstructures and properties of rapidly solidified Y₂O₃ doped Al₂O₃/ZrO₂ composites prepared by combustion synthesis. Scripta Materialia, Vol. 55, 2006, p. 819.

Search CrossRef
Zhao Z. M., Zhang L., Song Y. G., Wang W. G. Al₂O₃/ZrO₂(Y₂O₃) self-growing composite prepared by combustion synthesis under high gravity. Scripta Materialia, Vol. 58, 2008, p. 207.

Search CrossRef
Ni X. H., Sun T., Liu X. Q., Gu Q. H., Meng X. F. Size dependent strength of fiber eutectics and transformation particles composite ceramic. Applied Mechanics and Materials, Vol. 44-47, 2011, p. 2264.

Search CrossRef
Ni X. H., Liu X. Q., Han B. H., Zhong G. H., Sun T. Bridging toughening mechanism of fiber eutectics and transformation particles composite ceramic. Advanced Materials Research, Vol. 177, 2011, p. 178.

Search CrossRef
Li B. F., Zheng J., Ni X. H., Ma Y. C., Zhang J. Effective elastic constants of fiber-eutectics and transformation particles composite ceramic. Advanced Materials Research, Vol. 177, 2011, p. 182.

Search CrossRef
Ni X. H., Li B. F., Zhong G. H., Zhao L. Size dependent thermal expansion coefficient of rod-shaped oxide eutectic ceramic. Advanced Material Research, Vol. 105-106, 2010, p. 146.

Search CrossRef
Sun T., Ni X. H., Liu X. Q., Han B. H., Cheng Z. G. Analysis of damage strain field for ceramic composite with eutectic interphases. Chinese Journal of Computational Mechanics, Vol. 29, 2012, p. 527.

Search CrossRef
Liu X. Q., Ni X. H., Cheng Z. G., Li B. F., Zhao L. Size dependent residual stress field of composite ceramic with eutectic interphases. Transferability and Applicability of Current Mechanics Approaches, Fracture Mechanics and Structural Integrity, 2009, p. 397.

Search CrossRef
Chen I. W., Reyes-Morel P. E. Implication of transformation plasticity in ZrO₂ – containing ceramics: I, shear and dilation effects. J. Am. Ceram., Vol. 69, 1986, p. 181.

Search CrossRef
Lambropoulos J. C. Shear, shape and orientation effects in transformation toughening. Int. J. Solids Structure, Vol. 22, 1986, p. 1083.

Search CrossRef
Ni X. H., Liu X. Q., Wang J. Y., Lu X. B. The toughing action of comprehensive transformation on mixed mode II-III ceramics. Key Engineering Materials, Vol. 280-283, 2005, p. 1779-1782.

Search CrossRef

About this article

Received

06 April 2014

Accepted

03 May 2014

Published

15 May 2014

Keywords

damage rod-shaped eutectic

transformation particle

crack bridging toughening mechanism

pull-out toughening mechanism

stress-induced transformation toughening mechanism

fracture toughness

Acknowledgements

This work is supported by the National Natural Science Foundation of China under Grant No. 11272355.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.