Abstract
Empirical mode decomposition (EMD), a self-adaptive time-frequency analysis methodology, is particularly suitable for processing the nonlinear and non-stationary time series, which can decompose a complicated signal into a series of intrinsic mode functions. Although it has the attractive features, the approach to construct the envelop-line in EMD has obvious shortcomings. A suggested improvement to EMD by adopting the optimized rational Hermite interpolation is proposed in this paper. In the proposed method, it adopts rational Hermite interpolation to compute the envelope-line, which has a shape controlling parameter compared with the cubic Hermite interpolation. In the meantime, one parameter determining criterion is introduced to guarantee the shape controlling parameter selection performs optimally. Besides the empirical envelope demodulation (EED) is introduced and utilized to analyze the IMFs derived from the improved EMD method. Hence, a new time-frequency method based on the optimized rational Hermite-based EMD combined with EED is proposed and the effectiveness was validated by the numerical simulations and an application to the reciprocating compressor fault diagnosis. The contributions of this paper are three aspects: Firstly, the definition of the best envelope is non-existent, some light is given about which envelope maybe better in this paper. Secondly, the optimal shape controlling parameter selection combined with rational Hermite interpolation is developed, leading to the significant performance enhancement. Thirdly, little research has been carried out on the fault diagnosis of the reciprocating compressor using EMD, the proposed method is a good start.
1. Introduction
Vibration analysis techniques have been widely used in detecting faults in rotating machinery in recent years [1]. However, the applications of the vibration to the reciprocating compressor fault diagnosis are rare, which is mainly due to the nature of the vibration generated by reciprocating compressor is strongly transient and non-stationary and presents a multiple impulse source property. Also, a number of methods are applied to process the vibrations signal of the reciprocating compressor. Wang et al. applied wavelet transform to diagnose the compressor valve [2]. A probabilistic neural network was proposed for automatic classification of a reciprocating compressor with seeded faults by Lin et al. [3]. Information entropy and SVM method was proposed to classify five types of valve faults by Cui et al. [4]. Wang et al. used wave matching and support vector machine to detect the reciprocating compressor valves fault [5]. Nevertheless, these advanced techniques represent their own limitations on the compressor oversized bearing fault diagnosis.
Empirical mode decomposition (EMD), proposed by N. E. Huang, is mainly used to analyze the nonlinear and non-stationary date [6]. EMD can adaptively decompose a multicomponent signal into a sum of simple components defined as intrinsic mode functions (IMFs), and due to the decomposition is only according to the inherent characteristics of the original signal, EMD is a fully self-adaptive analysis method. What’s more, the combination EMD with the Hilbert transform (known as the Hilber-Huang Transform, HHT) has been proved to be a powerful time-frequency technique and applied to many applications [7-9].
However, the major drawbacks of EMD method are to fit the local extrema of the signal with the cubic spline interpoaltion. The cuibc spline-envelope exists outstanding over and undershoot problems, which needs to further study. Spline type selection is the key step in the EMD method, which will influence the results directly [10]. Many reasearches have been carried out on the spline type. Alternating taut spline with cubic spline indicates slightly improvement was noted by Huang et al. (1998). Cubic spline interpolation is better than the liner was suggested by Rilling et al. (2003) [11]. To change the extreme interpolation, Hawley et al. replaced the cubic spline with trigonometric interpolation. Rather than fitting the maxima and minima to construct the upper and lower envelopes, Chen et al. used the B-splined to fit the combined extrema and then obtained the local mean [12]. Qin et al. introduced a new envelope algorithm of Hilbert-Huang Transform to fit the envelope of a signal with the extreme points [13]. Pegram et al. proposed an alternative spline methodology called rational spline, which has a tension parameter compared with the traditional cubic spline [14]. Yannis Kopsinis, et al. analyzed how to select better interpolation points to get the best envelope possible approximation and introduced the GA-based optimization of the piecewise polynomials interpolation [15].
All of the above-mentioned alternating methods have demonstrated the validity and effectiveness in the practical signal or synthetic signals analysis. However, litter research has been carried out on the optimum of the envelope-line selection of EMD. Since the piecewise cubic Hermite depends on the first derivatives of the interpolation points which exhibits more flexibility than the cubic spline interpolation and high computation efficiency [16, 17], appling the cubic Hermite to fit the local extrema can not only ensure the continuity and smoothness of the successive points but also have the excellent characteristic of shape preservation, which is especially suitable for processing the strongly non-strongly and non-linear signal.
However, the cubic Hermite interpolation can’t adaptively adjust the shape of the curve with the changing local feather of the waveform in the sifting process, which needs further research and improvement. Focused on the above problems, the optimized rational spline-based EMD is proposed in this paper, which uses an alternative interpolation methodology called rational Hermite to construct envelope curves between extreme points. Compared with the cubic Hermite, it has a shape controlling parameter. The rational Hermite can control the shape of the curve by the parameter Therefore, when using the rational Hermite interpolation to construct the envelope, the shape controlling parameter can be varied in the sifting process. Furthermore, one fitness function combined with Genetic Algorithm is used to automatically select the shape controlling parameter in each sifting process. To further investigate the performance of the proposed method, three assess indicators are introduced. At last, the optimized rational Hermite-based EMD method is introduced into the simulation signal analysis and a comparison is made with the cubic Hermite-based EMD and the cubic spline-based EMD method. The comparison results show the superiority of the proposed method. Furthermore, the vibration signal of the reciprocating compressor with the oversized bearing clearance fault is analyzed by the optimized rational Hermite-based EMD method. The practical signal analysis results demonstrate the validity and effectiveness of the proposed method in reciprocating compressor fault diagnosis.The rest of this paper is organized as follows: the main steps of EMD and the over and undershoot problems of the cubic spline interpolation are discussed in section 2. In section 3 the rational Hermite interpolation is introduced. The shape controlling parameter selection process and three assessing indicators are described. Simultaneously, the comparisons of simulation signal analysis between optimized rational Hermite-based EMD, cubic Hermite-based EMD and the traditional EMD method are discussed in section 4, which show that the better decomposition results can be obtained by the improved method. The analysis results of the reciprocating compressor vibration signal with oversized bearing fault are given in section 5. Finally, the conclusions about the diagnostics capability of the optimized rational Hermite-based EMD method are drawn in section 6.
2. Review of the envelope problem in HHT
EMD is an adaptive decomposition method proposed by Huang [6]. The main idea of the EMD method is using the mean value of the upper and lower envelopes of the original signal to describe the “instantaneous equilibrium position”. And then extract the intrinsic mode functions of the signal.
There are three main steps to get IMF from signal :
1) Find out all the extreme points of the signal and then construct the upper and lower envelopes with the local maxima and minima by using cubic spline interpolation.
2) Set the mean of the upper and lower envelopes to be .
3) Subtracting from , we obtain :
If satisfies the following two conditions, we consider it as an IMF.
a) In the whole date set, the number of zero crossings and the number of extrema must be equal or differ at most by one;
b) At any time, the mean between the local maxima envelope and the local minima envelope is zero.
Otherwise take as a new signal and repeat the process above until the is an IMF, and set the as . Usually, the repeating subtracting process will stop until the standard deviation (SD) value, which evaluate the repetitiveness of the signal, is less than a determined value between 0.2 and 0.3:
Then, note that and consider as a new . We can decompose other IMFs from the original signal one by one. The decomposition is terminated until the residual becomes a monotonic function.
Finally, the original signal can be expressed as:
For each IMF, we obtain their significant instantaneous frequency by the following formula:
where is the analytic signal of component calculated by Hilbert Transform:
The Hilbert Spectrum can be defined as:
Respectively, where:
From the above sifting process, it can be known that the envelope-line can influence the whole process. When the cubic spline interpolation is applied to produce the envelope-line, the over and undershoots problems will often occur, which will has an adverse impact on the decomposition results. Mathematically, given the +1 points, in each interval , the piecewise cubic spline expression can be written as:
The boundary condition is:
From the fitting function, due to the first and second derivatives at each point can’t guarantee that the first derivatives of and equal to zero or have the same value, the over and undershoots problems would not be avoided [18]. The envelope error will transfer into the local mean and the whole signal by the iterative nature of the sifting process, which will result in inaccuracy and unreliable decomposition results.
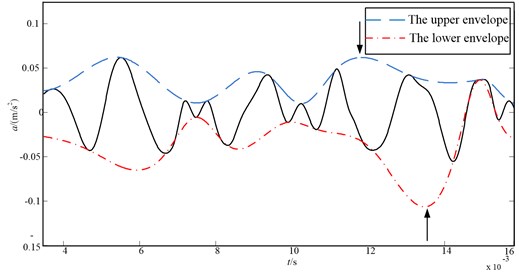
The cubic spline fits the maxima to construct the upper envelope (blue line) and fits the minima to construct the lower envelope (red line) in Fig. 1. The upper and lower envelopes have both over and undershoot problems denoted by arrows. The reason of the over and undershoot problems often occurring in the cubic spline interpolation is that the cubic spline lacks the adequate flexibility when fitting the local extrema [13]. Therefore the envelope algorithm needs further research.
Fig. 1Section of nonlinear and non-stationary signal
3. A new envelope interpolation algorithm
3.1. Cubic Hermite interpolation
Considering that the cubic spline interpolation is of second-order smoothness (second-order derivable), while the cubic Hermite is only first-order smoothness. Therefore the piecewise cubic Hermite interpolation algorithm is often proposed as potential improvement to the EMD method [16, 17]. The detailed mathematical cubic Hermite interpolation is as follows:
Given a series of discrete date and the is the value at time ( 0, 1, 2,…, ), is the first derivative at each time , , and is any real numbers. Then in each , can be written as:
where , , and are basis function of the cubic Hermite interpolation and can be expressed as [17]:
From the Eq. (11), the defined basis functions satisfy the following condition:
Also , .
The cubic Hermite is used in place of cubic splines for interpolating the maxima and minima envelopes within the EMD sifting process. However, after the experiments the author find that sometimes the cubic Hermite interpolation algorithm is too flexible which may even cause the obvious break points. What’s more, once the interpolation conditions are given, the shape of the curve is fixed which also means the curve approximation effectiveness is unchangeable. Since the fluctuant trend of the extrema of the produced new time series is uncertain, which requires the shape of the curve is changeable, the shape of the cubic Hermite interpolation can’t be adjusted with the changing local feather of the waveform in the sifting process. It needs further study and improvement.
3.2. Rational Hermite interpolation
Based on the discussion above, the cubic spline interpolation lacks adequate flexibility due to the second-order smoothness, the cubic Hermite interpolation can satisfy the flexibility requirement depending on the first derivatives of the interpolation points. However it lacks enough smoothness. To overcome the shortcomings of cubic Hermite interpolation, the alternative spline interpolation approach called rational Hermite interpolation is proposed.
The rational Hermite interpolation has a shape controlling parameter compared with the cubic Hermite interpolation which can control the shape of the spline as well as retain the desirable characteristics of the cubic Hermite interpolation. The basis function selection is key step to construct the rational Hermite interpolation. This paper proposed a four quartic polynomial basis function which has the advantages of simple structure, efficiency of computation and reliable outcomes.
Definition 1. Given 0 1, and is the real number, then the four quartic polynomial can be described as the basis function of the rational Hermite interpolation:
Also some property of the defined basis functions can be obtained after the calculations, which satisfied followings:
and , .
The results show that: the defined basis functions have the absolutely same properties with the basis function of piecewise cubic Hermite interpolation. Especially, when the 0, the rational Hermite interpolation defaults to the cubic Hermite interpolation. So the four quartic polynomial can be considered as the extension of the basis function of piecewise cubic Hermite interpolation. What’s more, the defined basis functions can be taken as the definition of the rational Hermite interpolation. Due to the parameter , the shape of the splines constructed by the rational Hermite can be adjusted by changing the value of the parameter, which is an improvement of the cubic Hermite interpolation.
Definition 2. Given a series of discrete date (, , ) (), the is the local maxima and minima at time and the is the first derivative at each time (). The aim is to fit the two points to interpolate the segments. The rational Hermite interpolation can be constructed in each [ ():
where , , is the parameter used to control the shape of the spline and , , and are the basis functions of the rational Hermite interpolation. It has been proved that the proposed interpolation is first-order smooth continuous and derivable.
Fig. 2The first sift of the IMF1(t) for the synthetic signal, a range of parameter λ combined with rational Hermite interpolation to construct the upper and lower envelopes
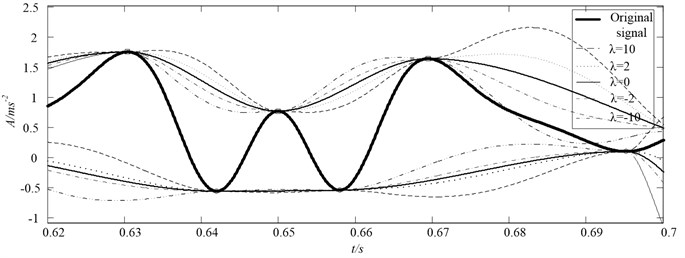
The rational Hermite spline has a variable parameter , which allows the shape of the spline can be controlled. In Fig. 2, the rational Hermite interpolation is applied to a section of the synthetic signal. The figure shows the first sift of for a range of parameter . The envelopes constructed by the rational Hermite with ranging from –10, –2, –1, –0.5, 0 (cubic), 0.5, 1, 2, 10 are presented in the figure. The shapes of the envelopes are progressively changed as is varied. Also from the figure we can get the conclusion that: where the cubic Hermite performs well, the rational Hermite performs similarly across the range of parameter settings.
3.3. The selection of shape controlling parameter
As mentioned above, the rational Hermite interpolation formula possesses a parameter that enable the user to select the shape of the interpolation in the sifting process. Different shape controlling parameter of rational Hermit interpolation will produce different EMD decomposition results. To realize accurate decomposition and be more user friendly, it is necessary to find ways of automatically selecting the shape controlling parameter. There is no objective way to determine the shape controlling parameter, since there is no definition of the best envelope in Huang [10]. However, some hidden information embedded in the signal sifting process can inform which envelope may be better.
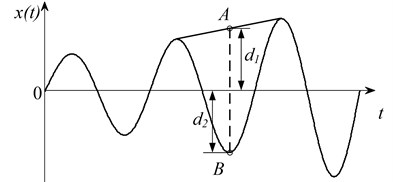
Recently, Cheng [19] investigated the typical single component signals that have the physical meaning of instantaneous frequency, such as amplitude modulated signal shown in Fig. 3. One conclusion can be obtained from Fig. 3. Connecting the extremum with straight line and then it intersects the vertical axis line which is through the mid-extreme at point A. The distance of A to axis, , is equal or approximated equal to the distance of B to axis, , which means A and B is symmetric or approximated symmetric about the horizontal axis. Furthermore, the conclusion is also suitable for sine (or cosine) signal, frequency modulation (FM) signal and amplitude and frequency modulated (AM-FM) signal.
Fig. 3The amplitude modulated waveform and the A and B point is symmetric or approximated symmetric about the horizontal t
For a series of extrema of a signal which has a group of three successive extrema (), () and () (). To locate the calculated point () of a signal connect each pair of two extrema (two minima or two maxima) points () and () by straight lines, and then denote the calculated point at the middle extremum points () time by .
Mathematically, at each time can be written as [20]:
Then the obtained point () can be seen as the criterion point of the analyzed signal [20].
The theorem can be simply explained in the following way. The EMD method can decompose a complicated signal into a sum of IMFs, which should satisfy the two conditions mentioned in section 2. In fact the two IMF condition is aim to ensure the obtained IMFs have meaning in instantaneous frequency. Cheng [19] put forward a new approach which describe the definition of the monocomponent with physical meaning signal (called intrinsic scale components (ISC)) in another way. Due to the two definitions can also describe the monocomponent, it is necessary to combine them together. The description of ISC is introduced in the EMD sifting process. Namely, the envelope interpolation of the any two adjacent maxima (or two adjacent minima) should try to be close to or pass through the calculated symmetric point of middle minimum point (middle maximum point), and then it enhances the description of the local geometrical information based on the original monocomponent definition of EMD. As a result, it will enhance the reliability of interpolation to get better envelope interpolation. Based on the above analysis, the symmetric point of middle extremum can be considered as the criterion point used to select shape controlling parameter of the rational Hermite interpolation.
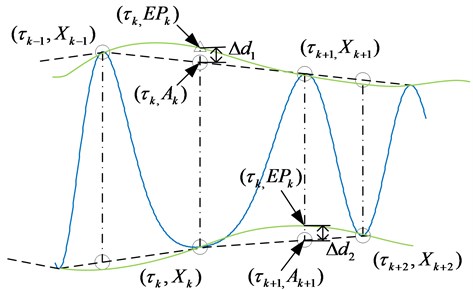
The illustration of the parameter selection criterion can be expressed as:
where and are the envelope interpolation point at the middle extrema points () time and criterion point respectively. For further explanation, and are described as “△” and “○” respectively in Fig. 4. The parameter determining index is defined to minimize the distance between the criterion point by in Eq. (16) and the envelope point , ().
Fig. 4Illustration of the parameter determining index theory
4. The optimized rational Hermite-based EMD method
4.1. The optimized rational Hermite-based EMD scheme
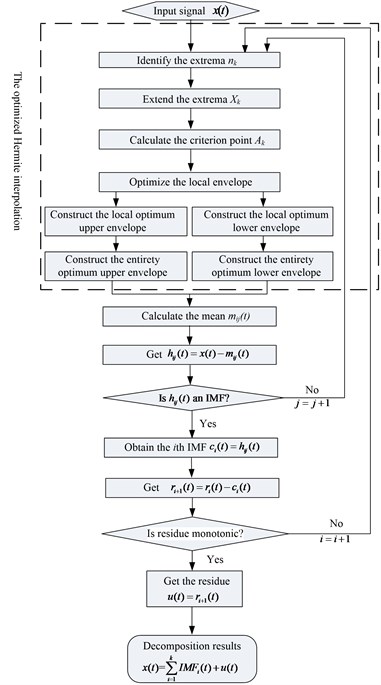
As discussed above, the crux of the optimized rational Hermite-based EMD method is applying the rational Hermite interpolation to substitute the original cubic spline interpolation, and the corresponding symmetric points are used to fulfill the shape controlling parameter automatic selection. The detailed procedures are as follows.
Denote all local extrema of the original signal as (), and calculate the (). Since the calculate reference value of is rang from 2 to , it is need to extend the boundary of the data, which is done by the mirror-symmetric extension method. By doing this, two end extrema can be got and written as (, ) and (, ). And then by Eq. (16), we can got and .
Connect any adjant extrema by the rational Hermite interpoaltion to constuct the peicewise envelope, in which the shape controlling paremeter is varied by a given step. The calculated point is utilized as the criterion point and according to the Eq. (17), the optimum local upper envelope interpoaltion and loweer envelope interpoaltion can be got.
Repeat step (2), until all the local optimum envelope interpoaltion of the adjant maxima , and all the local optimum envelope interpoaltion of the adjant minma are calculated. Then connect all the and to construct the entirety upper envelope and , respectively.
Design the mean of upper and lower envelopes as :
After we obtain the local mean function, continue to fulfill the following steps of EMD, then the optimized rational Hermite-based EMD method can be realized.
A flow chart of the optimized rational Hermite-based EMD algorithm sifting process is presented in Fig. 5.
Fig. 5Flow chart of optimized rational Hermite-based EMD method
4.2. Three assessing indicators
4.2.1. Orthogonal index
An important property of the EMD algorithm is that the IMFs and the final residual are expected to be mutually orthogonal. The index is proposed to evaluate the orthogonality, which can be written as [21]:
where is the number of . is the length of the IMF. and are the th and th IMF at sifting step , respectively. is the original signal and is the residual after the EMD decomposition.
4.2.2. RMSE
Since the first two components obtained by ICD and LMD are in accordance with and , respectively. The root mean squared error (RMSE) is utilized to assess the decomposition accuracy. And the smaller RMSE value indicates the higher accuracy:
where and are the original defined component and the corresponding decomposed component, respectively.
4.2.3. The sifting steps of each IMF
Another significant aim of EMD decomposition is to minimize the number of sifts per IMF. Since least sifts per IMF would reduce the sifting iterative error. The sifts per IMF is less, the IMF can be considered better.
4.3. Empirical envelope demodualtion (EED)
To obtain the time-frequency distribution, the demodulation analysis is needed, among which the Hilbert transform (HT) is widely used to demodulate each IMF componment, then the instantaneous frequency (IF), instantaneous amplitude (IA) can be obtained. However, HT is restrincted by the Bedrosian and Nuttall theorems and also has heavy end effect caused by energy leakage for an incomplete waveform [22]. To overcome the shortcomings of HT, the empirical AM-FM decomposition is put forward by Huang and Wu. Based on the AM-FM decomposition, Cheng proposed a new demodulation technique called empirical envelope demodulation (EED) [23]. In this paper, the EED is applied to demodulate the derived IMFs.
5. Application to simulation signals
In this section, to validate the effectiveness of the proposed optimized rational spline-based EMD and EED method, considering the numerical simulations on multi-components signal as:
The simulation signal consists of two AM-FM components. Set sampling frequency 1000 Hz and the time is 2 s. The waveform of , , , are shown in Fig. 6. In order to identify the decomposition ability and superiority of the optimized rational spline-based EMD method, firstly, the multi-component signal given by Eq. (21) is decomposed by the optimized rational Hermite-based EMD method, and then replace the proposed method by the traditional EMD to decompose the same simulation signal. In addition, the range of the shape controlling parameter of the rational Hermite-based EMD is from –50 to 50 and the IMF criteria in the sifting process is the three threshold criterion which was proposed by Rilling and Flandrin [24] and the thresholds used in this paper are , and . The decomposition results are illustrated in Figs. 7, 8 respectively.
As we see from Fig. 7, the second and third IMF of original EMD method which are corresponding to the , of the simulation signal has slight distortion in the left and right end. While in the Fig. 8, the corresponding second and third IMF of optimized rational Hermite-based EMD method are much more close to the real components and has less distortion phenomenon. Additionally, the components of original EMD are more than the defined original components, which will lead to the decomposition error. In generally, the derived IMFs of the two methods are both close to the real components and have little difference, therefore, it is necessary to apply the three assessing indicators to illustrate which method is better, and the results are shown in Table 1.
Fig. 6Simulation signal and its three components
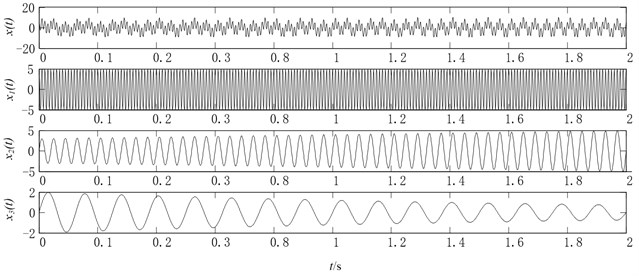
Fig. 7Original EMD decomposition results of simulation signal x(t)
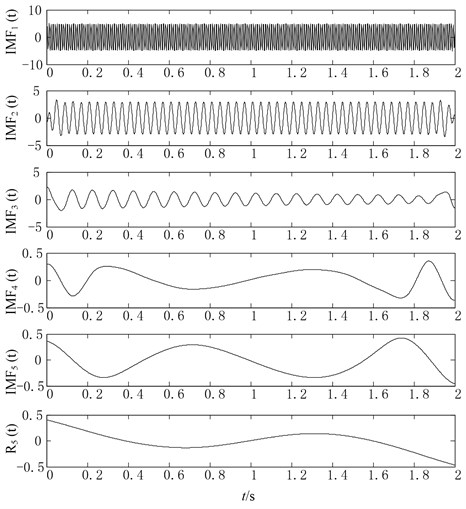
The following conclusion can be got from Table 1. To begin with, the RMSE of , and generated by improved EMD are all smaller than that of original EMD, which illustrate that the optimized rational Hermite-based EMD method (for convenience, called improved EMD method) can obtain the better approximations to the real components of the defined signal . Secondly, the number of sifts of each IMF generated by improved EMD (3, 2, 2) are also smaller than that of IMF’s generated by original EMD (5, 3, 2). At last, the improved EMD has a smaller value of OI compared with original EMD as well. In summary, the comparison analysis demonstrates the improved EMD is super to original EMD in components’ accuracy, iteration times and orthogonality.
Fig. 8The optimized rational Hermite-based EMD decomposition results of simulation signal x(t)
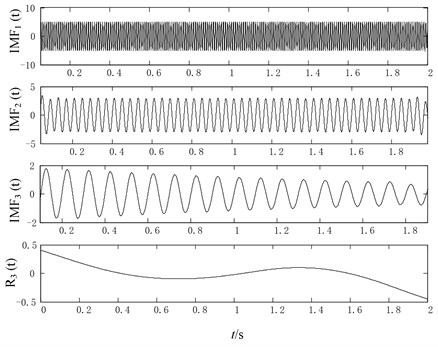
Table 1Three assessing indicators comparison for the original EMD and Optimized Hermite spline – EMD method
Methods | Orthogonal index | ||||||
RMSE | The number of sifts | RMSE | The number of sifts | RMSE | The number of sifts | ||
Original EMD method | 0.0852 | 5 | 0.0893 | 3 | 0.0120 | 2 | 0.0220 |
Optimized rational Hermite – EMD method | 0.0478 | 3 | 0.0574 | 2 | 0.0018 | 2 | 0.0189 |
The above analysis results can be explained in the following way. The optimized rational Hermite interpolation can adapt to the fluctuation of the extrema better than the cubic spline interpolation. In other words, the better envelopes can be obtained by the proposed interpolation approach, then the less iteration times will be needed to satisfy the IMF criteria. What’s more, the less iteration times will lead to less iteration error and the end effect will not spread into the signal.
Fig. 9The time-frequency distribution of the IMFs derived from the original EMD method
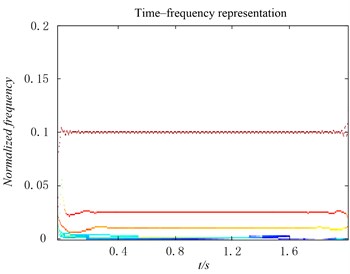
Fig. 10The HHT spectrum of the IMFs derived from the optimized rational Hermite-based EMD
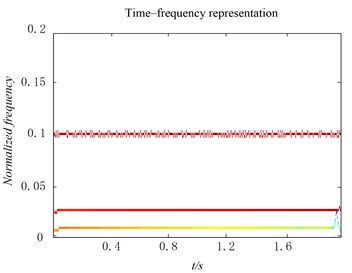
To do further research on the decomposition ability of the optimized rational Hermite-based EMD method, the EED demodulation technique is utilized to calculate the instantaneous frequency and instantaneous amplitudes, and the time-frequency distribution of the IMFs obtained by the two methods are shown in Figs. 9, 10, respectively. Compare the two figures, we can find that the time-frequency distribution with second and third IMF of original EMD are anamorphic and lose the physical meaning. On the contrary, the time-frequency distribution of IMFs derived from the improved EMD distort slightly, also the second IMF, whose IF is 25 Hz has a narrower bandwidth than that of original EMD method.
From the above analysis, it is clear that the optimized rational Hermite-based EMD method has advantage of decomposing more precise components, restraining the mode mixing and obtaining more accurate time-frequency distribution.
6. Applications to the reciprocating compressor fault diagnosis
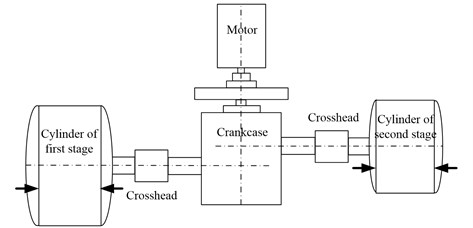
In order to validate the effectiveness of the proposed method, the optimized rational Hermite-based EMD is applied to diagnostic the reciprocating compressor fault. The experiment was conducted on the double-acting reciprocating compressor of 2D12 in a large-scale in Da Qing, China, whose structure are shown in Fig. 11. The location of the accelerometer is on the bottom of slide on the first crosshead, where the fault frequency is easy to find. The rating power of the reciprocating compressor is 500 kW, and the rotating speed is 496 r/min with sample frequency 50000 Hz. At that time, the shell bearings vibrated so intensely that the amplitude of the vibration value exceeded the safety threshold, which leaded to the online monitoring system giving alarm. A few days later, the vibration of the reciprocating compressor was even more violent, and the gas compressor station was stopped for repairmen. It was found that the shell bearings was broken which resulted in the oversized bearing fault of the big – end bearing, and the clearance value was 0.35 mm. To do further research of the fault patterns, EMD method was used to analyze the vibration signal.
Fig. 11The structure of the reciprocating compressor and the sketch of the air valve
The vibrations of the reciprocating machines usually show a transient nature and undergo interference which is generated by the transient moving impacts and contacting with other components [16]. Also when the clearance fault happens, the measured vibration signal represents complex, multi-component and non-stationary characteristics, the EMD method can decompose a complicated signal into a serial of IMFs adaptively. Moreover, the optimized rational Hermite interpolation has advantage of computing the more accuracy envelope-line by fitting the highly non-stationary signal. Therefore, the optimized rational Hermite-based EMD method is especially suitable for processing the oversized bearing clearance fault signal. Firstly, the EMD method is applied to decompose the signal into a number of IMFs, and then the fault frequency of gear was found through the amplitude spectrums of the IMF components [25]. In order to process the modulated features of the reciprocating compressor fault vibration signal, the optimized rational Hermite-based EMD combined with the amplitude analysis method is applied to the reciprocating compressor fault diagnosis.
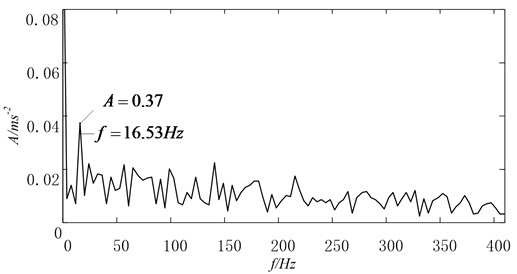
Application to the oversized bearing clearance fault diagnosis of the reciprocating compressor. Typical oversized bearing clearance fault vibration signal of the reciprocating compressor is illustrated in Fig. 12. Also the spectrum is shown in Fig. 13. As seen from the frequency domain, the energy is mainly concentrated in the high frequency, any further detailed information can’t be obtained from the spectrums.
Fig. 12The vibration acceleration signal of the reciprocating compressor
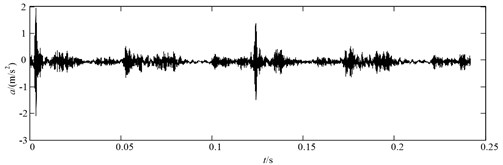
Fig. 13The spectrum of the reciprocating compressor vibration
Applying the optimized rational Hermite-based EMD method to the vibration signal with clearness fault condition, 8 IMFs and a residual were obtained. Since the IMFs with different oscillatory modes are listed from high frequency to low frequency, and the fault information are mainly embedded in the high frequency, only the first three IMFs are shown in Fig. 14. As a comparison, the original EMD method is also applied on the vibration signal with clearness fault condition, the decomposition results are shown in Fig. 15.
Fig. 14Optimized Hermite-based EMD decomposition results of the vibration acceleration
Fig. 15Original EMD decomposition results of the vibration acceleration
The vibration signals of the reciprocating compressor measured by the senior present multi-component AM-FM feather. The vibration signal can be decomposed into a set of mono-component IMFs by the EMD method, and then the demodulation technique is used to extract the fault signature. Since the Hilbert transform has many defects, the EED is proposed [23]. The modulated feather could be extracted effectively by performing the spectrum analysis of the instantaneous amplitudes of each IMF component.
Moreover, in order to effectively compare the three methods, the normalized amplitude spectrums of decomposed by three methods are illustrated in Figs. 16, 17. Seen from the figures, although the two methods can identify the fault frequency of the reciprocating compressor, the optimized rational EMD method shows the clearest fault signature and the least interference frequency. The amplitude spectrum of the first IMF decomposed by the traditional EMD method is smaller than the optimized Hermite-based EMD method, which means the optimized Hermite-EMD method can improve the quality of the decomposition and get the more accurate component than the original EMD method. Simultaneously, it can be seen that the amplitude spectrum of the decomposed by the cubic Hermite-based EMD has a bigger value compared with the original EMD method, which indicates the Hermite interpolation combined with EMD is more suitable than the cubic spline interpolation in the diagnosis of reciprocating compressor. The detailed explanation is due to the rational Hermite interpolation has lower restrains and excellent characteristic of shape preservation than cubic spline interpolation. Due to the optimum adjustable curve shape with parameter , the envelope approximation accuracy be further improved, which can avoid the over and undershoot problems of cubic spline interpolation effectively.
Fig. 16The first IMF with amplitude spectrum by the optimized Hermite-based EMD method
Fig. 17The first IMF with amplitude spectrum by original EMD method
Moreover, Fig. 18 gives a section of data intercepted from the reciprocating vibration signal in the sifting process and the upper and lower envelopes of the two approaches interpolation are compared with each other. From the Fig. 18, it can be found that the cubic spline interpolation (red dashed line) to construct the envelopes has severe over-and undershoot problems, whereas, the optimized Hermite (blue line) is better fitting the extrema than the cubic spline interpolation, which can overcome the over and undershoot shortcomings of cubic spline interpolation effectively.
Fig. 18The envelopes of the optimized Hermite interpolation (blue line) and cubic spline (red dashed line) interpolation
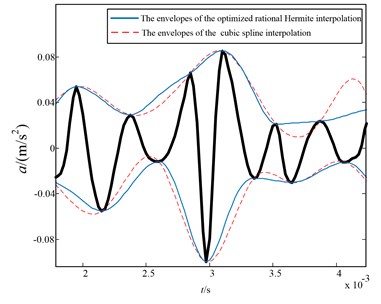
The analysis results of practical reciprocating compressor vibration signal demonstrate that the optimized rational spline interpolation is more flexible than the cubic spline interpolation and smoother than the cubic Hermite interpolation which can improve the reliability and accuracy significantly compared with the original cubic spline interpolation.
7. Conclusions
This paper put forward a new envelope algorithm for EMD, the optimized rational Hermite interpolation approach, which inherits the advantage of good smoothness and flexibility compared with the cubic spline interpolation. Also a proper value selection criterion for is introduced which can guarantee the rational Hermite interpolation performs optimally. Besides the demodulation technique EED is introduced which can avoid the drawbacks of HT. Therefore, a new time-frequency analysis based on the optimized rational Hermite-based EMD and EED is proposed, which is super to original HHT in processing the nonlinear and non-stationary time series.
References
-
Staszewski W., Tomlinson G. Application of the wavelet transform to fault detection in a spur gear. Mechanical Systems and Signal Processing, Vol. 8, 1994, p. 289-307.
-
Wang Y., Liao M., Zhao T. Application of the wavelet transform to fault diagnosis in compressor valves. Zhongguo Jixie Gongcheng/China Mechanical Engineering, Vol. 14, 2003, p. 1046-1048.
-
Yih-Hwang Lin, Wen-Sheng Lee, Chung-Yung Wu A novel signal processing approach for valve health condition classification of a reciprocating compressor with seeded faults considering time-frequency partitions. Journal of Marine Science and Technology, Vol. 21, 2013, p. 578-585.
-
Cui H., Zhang L., Kang R., Lan X. Research on fault diagnosis for reciprocating compressor valve using information entropy and SVM method. Journal of Loss Prevention in the Process Industries, Vol. 22, 2009, p. 864-867.
-
Qin Q., Jiang Z. N., Feng K., He W. A novel scheme for fault detection of reciprocating compressor valves based on basis pursuit, wave matching and support vector machine. Measurement, Vol. 45, 2012, p. 897-908.
-
Huang N. E., Shen Z., Long S. R., Wu M. C., Shih H. H., Zheng Q. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proceedings of the Royal Society of London, Series A: Mathematical, Physical and Engineering Sciences, Vol. 454, 1998, p. 903-995.
-
Li L., Xu G., Wang J., Cheng X. Automatic detection of epileptic slow-waves in EEG based on empirical mode decomposition and wavelet transform. Journal of Vibroengineering, Vol. 15, 2013.
-
Jikun B., Chen L., Zhipeng W., Zili W. An approach to health assessment for tools in milling machine. Journal of Vibroengineering, Vol. 15, 2013.
-
Yang Y., Chang K. Extraction of bridge frequencies from the dynamic response of a passing vehicle enhanced by the EMD technique. Journal of Sound and Vibration, Vol. 322, 2009, p. 718-739.
-
Huang N. E., Shen Z., Long S. R., Wu M. C., Shih H. H., Zheng Q. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proceedings of the Royal Society of London, Series A: Mathematical, Physical and Engineering Sciences, Vol. 454, 1998, p. 903-995.
-
Rilling G., Flandrin P., Goncalves P. On empirical mode decomposition and its algorithms. Eurasip Workshop on Nonlinear Signal and Image Processing, 2003, p. 8-11.
-
Chen Q., Huang N., Riemenschneider S., Xu Y. A B-spline approach for empirical mode decompositions. Advances in Computational Mathematics, Vol. 24, 2006, p. 171-195.
-
Qin S., Zhong Y. M. A new envelope algorithm of Hilbert-Huang transform. Mechanical Systems and Signal Processing, Vol. 20, 2006, p. 1941-1952.
-
Peel M., Pegram G., McMahon T. Empirical mode decomposition: improvement and application. Congress on Modelling and Simulation, 2007, p. 2996-3002.
-
Kopsinis Y., McLaughlin S. Investigation and performance enhancement of the empirical mode decomposition method based on a heuristic search optimization approach. Transactions on Signal Processing, Vol. 56, 2008, p. 1-13.
-
Tang Y. F., Li S. L. Time-frequency feature extraction from multiple impulse source signal of reciprocating compressor based on local frequency. Journal of Vibroengineering, Vol. 15, 2013.
-
Zhu W., Zhao H., Chen X. Improving empirical mode decomposition with an optimized piecewise cubic Hermite interpolation method. International Conference on Systems and Informatics, 2012, p. 1698-1701.
-
He Q., Liu Y., Kong F. Machine fault signature analysis by midpoint-based empirical mode decomposition. Measurement Science and Technology, Vol. 22, 2011, p. 15-17.
-
Cheng J. Y. Local characteristic-scale decomposition method and its application to gear fault diagnosis. Journal of Mechanical Engineering, Vol. 48, 2012, p. 64-71.
-
Frei M. G., Osorio I. Intrinsic time-scale decomposition: time-frequency-energy analysis and real-time filtering of non-stationary signals. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Science, Vol. 463, 2007, p. 321-342.
-
Peel M., McMahon T., Pegram G. Assessing the performance of rational spline-based empirical mode decomposition using a global annual precipitation dataset. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Science, Vol. 465, 2009, p. 3-52.
-
Feldman M. Theoretical analysis and comparison of the Hilbert transform decomposition methods. Mechanical Systems and Signal Processing, Vol. 22, 2008, p. 509-519.
-
Cheng J., Zheng J., Yang Y. Empirical envelope demodulation approach based on local characteristic-scale decomposition and its applications to mechanical fault diagnosis. Chinese Journal of Mechanical Engineering, Vol. 48, 2012, p. 87-94.
-
Rilling G., Flandrin P., Goncalves P. On empirical mode decomposition and its algorithms. Workshop on Nonlinear Signal and Image Processing, 2003, p. 8-11.
-
Huang N. E., Shen Z., Long S. R., Wu M. C., Shih H. H., Zheng Q., et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proceedings of the Royal Society of London, Series A: Mathematical, Physical and Engineering Sciences, Vol. 454, 1998, p. 903-995.
About this article
The research is supported by National Natural Science Foundation of China (No. 11172078) and Important National Basic Research Program of China (973 Program-2012CB720003), and the authors are grateful to all the reviewers and the editor for their valuable comments.
