Estimation of mode shapes expanded from incomplete measurements

1. Introduction

The information on complete mode shapes is necessary for the subsequent analysis and design of a dynamic system. However, it is not practical to collect a full set of mode shapes, and the data obtained from vibration testing cannot be used to measure all of the modes. The problem can be overcome by modal reduction or data expansion, i.e., either reduce the system matrices to the number of measured DOFs or conversely expand the measured modal vectors to the full size of the finite element model matrices. A full set of mode shapes should be expanded in the satisfaction of measured data.

Most of the utilized expansion techniques involve the use of the finite element model as a mechanism to complete the unmeasured DOFs from the experimental model. Imregun and Ewins [1] presented mode shape expansion methods to estimate the modal displacements at unmeasured coordinates using the incomplete set of measured data together with a corresponding finite element model. Levine-West et al. [2, 3] evaluated the robustness and reliability of the Guyan static expansion method, the Kidder dynamic method, the Procrustes method, and the penalty method along with least-squares minimization techniques. Dubbaka and Houghton [4] provided a correction method to modify the measured mode shapes by restricting the orthonormality and by applying the constraint rules. Based on a dynamic modal expansion that minimizes the residual error in the eigenvalue equation for each measured mode, Kenneth and Francois [5] presented an algorithm for expanding the measured mode shapes obtained from modal testing of the full set of DOFs of a corresponding finite element model. Ewins [6] presented some definitions and a very concise summary of each of the major algorithms for the updating problem together with some discussion of how and when each of these might be considered for use in practice. Chen [7] introduced an approach for expanding incomplete experimental mode shapes to consider the modeling errors and the uncertainties. Liu [8] presented a method for expanding incomplete experimental mode shapes by measured data for master DOFs and constant values for slave DOFs. Skafte et al. [9] introduced an expansion method to predict the mode shape coordinates and responses in unknown DOFs based on the local correspondence principle. Liu et al. [10] proposed a non-iterative mode shape expansion method based on coordinate decomposition and modeling errors between the finite element model and the experimental structure.

The analytically derived eigenmodes of a modal model do not match with the experimental results so that they cannot be utilized in the analytical model. The discrepancies result from the measurement, equipment, and manufacturing errors. Thus, the analytical eigenmodes should be modified for observing the dynamic characteristics of the system. The updated modal data cause the mass and stiffness matrices of the dynamic system to be modified.

Friswell and Mottershead [11] provided a comprehensive overview that illustrates many of the different techniques and issues involved in updating a finite element model. They showed the importance of several areas in model updating dedicated to modal methods. Baruch [12, 13] proposed a method in which the stiffness matrix based on the measured mode shapes obtained from vibration tests is corrected by minimizing a norm to use the positive definite symmetric mass matrix as the weighting matrix. Berman [14] described the change in the mass matrix required to satisfy the orthogonality relationship using a minimum-weighted Euclidean norm and the method of Lagrange multipliers. Berman and Nagy [15] proposed a direct method to identify a set of minimum changes in the analytical matrices that force the eigensolutions to agree with the test measurements. Kabe [16] adjusted the stiffness matrix such that the percentage change to each stiffness coefficient is minimized. The method preserved the physical configuration of the analytical model and reproduced the modes used in the identification. Caesar and Peter [17] discussed two methods for the direct updating of mathematical models based on modal test data. Minimizing the cost functions of the difference between analytical and desired physical parameter matrices, Lee and Eun [18, 19] derived the corrected parameter matrices by utilizing the Moore-Penrose inverse matrix.

The eigenmodes of the finite element model are expanded by minimizing the discrepancies between the measured modal data and those obtained by the analytical model. The expansion process is performed in the satisfaction of measured data contaminated by external noise. The method is performed under the assumption that the analytical mass and stiffness matrices are consistently maintained during the expansion. The inconsistency between the analytical and estimated mode shapes due to the external noise can be expressed by the variation in the parameter matrices perturbed from the analytical parameters. This study presents the mathematical forms to correct the parameter matrices utilizing the expanded mode shapes. A numerical experiment illustrates the validity of the proposed method.

2. Formulation

Developing an initial theoretical model constructed for analyzing the dynamics of a structure can be refined, corrected, or updated, using measurements on the actual structure, has become one of the most demanding and demanded applications for modal testing. The number of measured DOFs does not usually match with a full set of model DOFs, so expansion of the mode shapes is necessary. The estimated mode shape data provide the basic information required to predict the parameter matrices of mass and stiffness.

The dynamic behavior of a structure of free vibration without damping that is assumed to be linear and approximately discretized for $n$ DOFs can be described by the equation of motion as:

where $\mathbf{M}$ and $\mathbf{K}$ denote the $n\times n$ analytical mass and stiffness matrices, and $\mathbf{u}={\left[\begin{array}{llll}{u}_1& u_2& \cdots & u_n\end{array}\right]}^{\mathrm{T}}$. Assuming harmonic motion, the eigenfunction can be written by:

where ${\omega }^2$ is an eigenvalue and $\widehat{\mathbf{\varphi }}$ denotes the corresponding eigenvector obtained by eigenfunction.

The eigenmodes at unmeasured DOFs should be estimated using the measured modes and the analytical parameter matrices, such as the mass and stiffness matrices. Assume the experimental mass and stiffness matrices satisfy the eigenfunction during the data expansion. Assuming that the mode shapes corresponding to $m$ DOFs at the first $r$ eigenvalues were measured, it can be written by:

where $\mathbf{A}$ represents an $m\times n$ Boolean matrix to define the measurement DOFs, $\mathbf{\varphi }$ is the $n\times r$ actual mode shape matrix, and $\mathbf{B}$ denotes the $m\times r$ measured data matrix. The mode shape matrix can be divided into the $m\times r$ measured and the $\left(n-m\right)\times r$ unmeasured mode shape matrices.

The actual mode shape $\mathbf{\varphi }$ in Eq. (3) does not agree with the analytical mode shape $\widehat{\mathbf{\varphi }}$ in Eq. (2). Importing the analytical mass matrix as the weighting matrix, the mode shape $\mathbf{\varphi }$ is such that the performance index defined as:

is minimized over all $\mathbf{\varphi }$ that satisfy the constraint equation. In this work, the measurement data set of Eq. (3) for data expansion is utilized as the set of constraint conditions.

The measurement data set is modified as:

Solving Eq. (5) with respect to ${\mathbf{M}}^{1/2}\mathbf{\varphi }$, it results in:

where $\mathbf{y}$ is an arbitrary matrix and the superscript ‘+’ denotes the Moore-Penrose inverse matrix. Imposing the minimization condition on the performance index of Eq. (4), it leads to:

Solving Eq. (7) with respect to the arbitrary matrix $\mathbf{y}$, we obtain:

where $\mathbf{z}$ is another arbitrary matrix. Inserting Eq. (8) into Eq. (6), it is derived as:

Premultiplying both sides of Eq. (9) by ${\mathbf{M}}^{-1/2}$, the expanded mode shape matrix can be obtained as:

Eq. (10) represents the measured mode shape matrix as well as the unmeasured mode shape matrix to be estimated. The estimated mode shapes include the effect of the measured data as well as the external noise.

The mode shape data perturbed by the external noise can be utilized in updating the mass and stiffness matrices. Substituting the estimated mode shape $\mathbf{\varphi }$ and the perturbed parameter matrices into Eq. (2), it can be written as:

where $\mathrm{\Delta }\mathbf{K}$ and $\mathrm{\Delta }\mathbf{M}$ represent the variation in stiffness and matrices, respectively, caused by the change of analytical mode shape due to the external noise. Considering the first s modal data and arranging Eq. (11), it can be written by:

Solving Eq. (12) with respect to the variation in stiffness and mass matrices, it yields that:

where the superscript ‘+’ denotes the Moore-Penrose inverse matrix. The solution of Eq. (13) denotes the variation in parameter matrices due to the existence of external noise. Eq. (13) can be widely utilized in updating the parameter matrices perturbed by other causes, such as structural damage, except the external noise. The validity of the proposed method is illustrated in a numerical experiment.

3. A numerical experiment

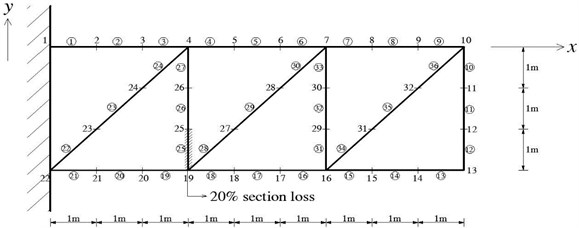
The expansion of measured mode shapes and the update of parameter matrices of a two dimensional three-story building structure model, shown in Fig. 1, were performed to investigate the applicability of the proposed method. The frame was modeled by 32 nodes and 36 elements, and the nodal points and the members of the frame model are numbered in the figure. Each node of the element possesses three degrees of freedom: displacement $u$ in the $x$ direction; displacement $v$ in the $y$ direction; a rotation about $z$-axis, $\theta$. The element ○25 in the frame was modeled as a 20 % area loss section. The planar frame element includes both axial and bending deformation. The measurement data on the rotations were not collected because of the measurement difficulty. The parameter values of the structure were chosen to be elastic modulus $E=\text{2.1×1}{\text{0}}^{\text{5}}$, cross-section area $A=\text{2}$, second moment of inertia $I=\text{200}$, mass per unit length $\stackrel{-}{m}=\text{0.02}$ in dimensionless unit. As a numerically simulated result, the 16 mode shape data corresponding to the $x$ and $y$ directions at 8 nodes (4, 7, 10, 13, 16, 19, 23, 29) were measured, and the others should be estimated by the proposed method.

Fig. 1A two dimensional frame structure model

The numerical experiment began with measurement data contaminated by 5 % external noise. The actual mode shapes, ${\mathbf{\varphi }}_i^m$, can be calculated for the simulated noise-free mode shapes, ${\mathbf{\varphi }}_i^0$, as follows:

where $\alpha$ denotes the relative magnitude of the error, and ${\sigma }_i$ is a random number variant in the range [–1, 1]. The noise includes the modeling and measurement errors.

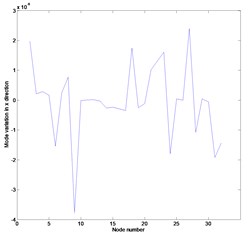
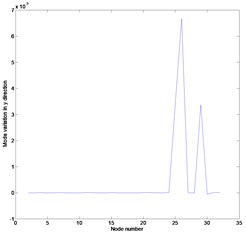
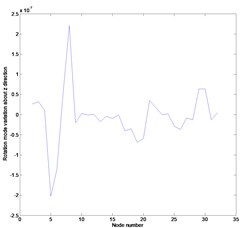
Fig. 2Mode variation in the first mode: a) mode variation in x direction, b) mode variation in y direction, c) rotation mode variation about z direction

a)

b)

c)

Fig. 3Mode variation in the second mode: a) mode variation in x direction, b) mode variation in y direction, c) rotation mode variation about z direction

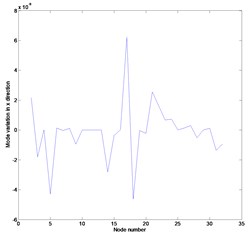
a)

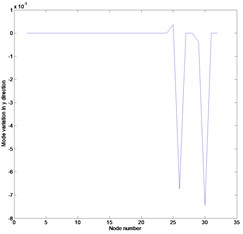
b)

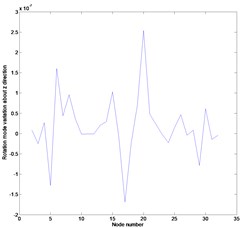
c)

Figs. 2 and 3 represent the mode variations between the actual and expanded mode shapes proposed by this work corresponding to the first and second mode, respectively. The mode shape expanded by Eq. (10) is found to be nearly identical with the actual one. It is shown that the measurement data given as the constraints coincide with the numerically obtained results and the other data are predicted in a small discrepancy. It is expected that the local increase in the mode variation in $y$ direction is caused by the section loss of the element ○25 as shown in Figs. 2(b) and 3(b). The proposed method provides enough information on the mode shape despite the external noise.

The discrepancies in the mode shapes due to the external noise can be expressed by the modification of the parameter matrices. Fig. 4 represents the variation in parameter matrices obtained by Eq. (13). The plots were obtained using the first two eigenvalues and the corresponding expanded mode shapes. The variations exhibit the values corresponding to the row and column arrays of stiffness and mass matrices. The mode shapes of the updated parameter matrices, including the variation in parameter matrices, lead to the expanded mode shapes shown in Figs. 2 and 3.

Fig. 4Variation in parameter matrices: a) stiffness variation, b) mass variation

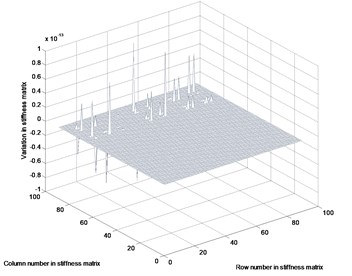
a)

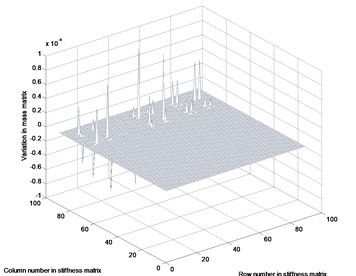
b)

4. Conclusions

Analytical mode shapes do not match with experimental results due to external noise, including modeling and measurement errors. Because it is impractical to measure the data at a full set of DOFs, the incomplete data set should be expanded to the full set. This work provided the expansion method to describe the full set of mode shapes in the satisfaction of measured mode shape data. The existence of external noise can result in the variation in parameter matrices, which were derived using the Moore-Penrose inverse matrix. The update method of parameter matrices was demonstrated to properly describe the variation in the parameter matrices. The proposed method can be widely utilized in updating the parameter matrices perturbed by other causes, such as structural damage, except the external noise. The numerical example illustrated the validity of the proposed method.