A reduced polynomial chaos expansion model for stochastic analysis of a moving load on beam system with non-Gaussian parameters

3.1. Theory [18]

Let $u(x,\theta )$ be a second-order random process and $\stackrel{-}{u}\left(x\right)$ denote the expected value of $u(x,\theta )$. The covariance function $C(x_1,x_2)$ of $u(x,\theta )$ is bounded, symmetric and positive definite and has the following spectral decomposition:

where ${\lambda }_n$ and ${\phi }_n\left(x\right)$ are the eigenvalues and the eigenvectors of the covariance function, respectively. They can be proved to be solution of the following integral equation:

Due to symmetry and the positive definiteness of the covariance kernel, the eigenfunctions are orthogonal and they form a complete set representing the covariance function. The eigenvectors can then be normalized according to the following criterion:

where ${\delta }_{ij}$ is the Kronecker delta. The random process $u(x,\theta )$ can then be written as:

where ${\xi }_n\left(\theta \right)$ is a group of uncorrelated random variables. As a special case, when $u(x,\theta )$ is a Gaussian random process, ${\xi }_n\left(\theta \right)$ is a set of standard Gaussian random variables with the following orthogonal properties:

where $E(\bullet )$ denotes the expectation value.

4.1. Theory [19]

For an element $u\left(\theta \right)$ from a set in the space spanned by the orthogonal basis, it has been proved that $u\left(\theta \right)$ can be written in the following form as:

where ${\mathrm{\Psi }}_i$ are the Hermite polynomials of ${\xi }_1\left(\theta \right)$, ${\xi }_2\left(\theta \right)$,…, ${\xi }_j\left(\theta \right)$, and ${\mathrm{\Psi }}_0=$ 1.0, ${\xi }_0\left(\theta \right)=$ 1.0. $b_k$ are the generalized Fourier coefficients with $k=$ (0, 1,…, $N$) and $N=1+\left(p+q\right)!/\left(p!q!\right)$. The series in Eq. (13) can be refined along the random dimension $\theta$ either by increasing the total number of random variables $q$ or the maximum order of polynomials $p$ included in the Polynomial Chaos (PC) expansion. The first refinement takes into account higher frequency random fluctuations of the underlying stochastic process, while the second refinement captures strong nonlinear dependence of the solution of this stochastic process [20].

The polynomials ${\mathrm{\Psi }}_k$ are orthogonal satisfying the relationship:

where $⟨\bullet ⟩$ denotes the inner product and the value of $⟨{\mathrm{\Psi }}_i^2⟩$ can be calculated analytically [19].

The generalized Fourier coefficients $b_k$ in Eq. (13) can be evaluated from:

4.2. Polynomial Chaos coefficients

Numerous approaches have been proposed to obtain the coefficients in the PCE model for a random process. Field et al. [21] proposed two methods with Monte Carlo simulation and numerical integration, respectively, to evaluate the coefficients. Non-intrusive method and Intrusive method were adopted by Reagan et al [22] for the analysis. The method using Latin Hypercube sampling and Fitting Regression model [23] will be introduced as follows due to its high efficiency and great accuracy, and it will be adopted in this paper to evaluate the coefficients in a one-dimensional PCE in the proposed reduced PCE model.

For a one-dimensional problem, i.e. $q$ in Eq. (13) equals to unity, consider the PCE truncated at the $p$th level:

where $b_i$, $i=$ 0, 1, 2,…, $p$, are the regression coefficients, and $\epsilon$ is the error of the model equation. Functions $f_1\left(\xi \right)=\xi$, $f_2\left(\xi \right)={\xi }^2-1$,…, $f_p\left(\xi \right)$ are the $p$th one-dimensional Hermite polynomials of $\xi \left(\theta \right)$.

It is noted that Eq. (16) can be regarded as a linear regression model. To evaluate the coefficients $b_i$, $n$ sample values, e.g. $z_1$~$z_n$, should be drawn from the standard random variable $\xi \left(\theta \right)$. With these sample values, the matrix form can be formulated as:

where $\mathbf{Y}={\left\{\begin{array}{llll}{y}_1& y_2& \cdots & y_n\end{array}\right\}}^T$, $\widehat{\mathbf{B}}={\left\{\begin{array}{llll}{b}_0& b_1& \cdots & b_q\end{array}\right\}}^T$, $\mathbf{e}={\left\{\begin{array}{llll}{\epsilon }_1& {\epsilon }_2& \cdots & {\epsilon }_n\end{array}\right\}}^T$ and:

and $y_1$ to $y_n$ are the sample values drawn from $u\left(\theta \right)$. Vector $\mathbf{e}$ includes the error terms. The sample values of $f_i\left(z_k\right)$ ($i=$ 1, 2,…, $p$) in Eq. (17) can be obtained from the Cumulative Density Function (CDF) of the random variables.

Using the least-squares method, the regression coefficients can be calculated as:

The fitted model and the residuals are:

5.1. The reduced PCE model

The KLE of a non-Gaussian process results in a set of deterministic coefficients multiplied by the corresponding uncorrelated non-Gaussian random variables $\left\{{\xi }_i\right(\theta \left)\right\}$. In the PCE of a non-Gaussian process, these uncorrelated non-Gaussian random variables are projected on the Polynomial Chaos basis. The dimension of PCE, denoted as $K_R$,to represent the stochastic response of a beam structure is determined according to the following [20]:

where $p$ is the maximum order of the Polynomial Chaos in PCE; $k_s$ is the number of K-L components required in the representation of the response which depends on the number of K-L components adopted in the representations of excitation forces and system parameters. For example, if the randomness in elastic modulus, mass density and excitation forces are independent and the Rayleigh damping is assumed, then $k_s=k_E+k_{\rho }+k_F$. Variables $k_E$, $k_{\rho }$, $k_F$ are the number of K-L components in the KLE of the Gaussian distributed elastic modulus, mass density and the excitation forces, respectively.

When a large number of K-L components is required inthe KLE of the excitation force, an extremely large number of Polynomial Chaos will be included in the PCE of the non-Gaussian random responses according to Eq. (20), and this leads to computation problem due to the limited capability of computer. This drawback limits the application of the SSFEM in the case with relatively simple excitation.

For the case with complex excitation forces, a reduced PCE model is proposed to avoid the curse of dimensionity of PCE in the response representation. The uncorrelated random variables in the KLE of the non-Gaussian random processes are assumed to be “uncoupled”. The spaces spanned by these “uncoupled” random variables are assumed to be mutually orthogonal, which results in keeping the terms of ${\mathrm{\Psi }}_i\left({\xi }_j\left(\theta \right)\right)$ in Eq. (13) and eliminating the terms of ${\mathrm{\Psi }}_i\left({\xi }_1\left(\theta \right),{\xi }_2\left(\theta \right),\dots ,{\xi }_j\left(\theta \right)\right)$ in the new reduced model. For example, when $p=$ 2 and $q=$ 2, Eq. (13) has the following form:

and in the new reduced model, the terms $b_4{\xi }_1{\xi }_2$, $b_7\left({\xi }_1^2{\xi }_2-{\xi }_2\right)$ and $b_8\left({\xi }_1{\xi }_2^2-{\xi }_1\right)$ are eliminated while other terms are retained. It is noted that the variance of a non-Gaussian system parameter is derived from the following equation:

Since the variance of terms retained are larger than those of the eliminated ones when they are of the same order [19], e.g. the variance of ${\xi }_1^3-3{\xi }_1$ and ${\xi }_1^2{\xi }_2-{\xi }_2$ are equal to 6 and 2, respectively, when the total number of the random variables $q$ increases, the summation of the variance of terms retained will be much larger than that of the eliminated ones. Therefore, the accuracy in the variance representation in Eq. (22) may still be maintained.

The reduced PCE approach on a non-Gaussian random process is implemented as follows: After the decomposition of a non-Gaussian random process $u(x,t,\theta )$ along the dimension $x$ and $t$ using the finite element method and KLE respectively, each uncorrelated random variable ${\xi }_i\left(\theta \right)$, which is assumed as “uncoupled” in this reduced PCE model, can be expanded as shown in Eq. (16) with a one-dimensional Polynomial Chaos. The dimension of PCE, $K_r$, required in a reduced PCE of order $p$ for the stochastic response becomes:

It is noted from Eqs. (20) and (23) that the dimension of PCE under this “uncoupled” assumption is significantly reduced compared with that in the “full” PCE. This allows the proposed algorithm to include a large number of K-L components in the PCE of the excitation force or the system parameters, with a trade off in the accuracy.

5.2. Modeling of the non-Gaussian system

5.3. Response statistics

Eq. (37) can be solved by employing the Newmark-$\beta$ method to obtain the deterministic coefficients in the reduced PCE for the responses, and the first two response statistics of the stochastic nodal displacement vector can be evaluated as:

where the subscript “$R$” denotes the random nodal displacement vector of the beam structure. The stochastic displacement of the beam structure at position $x$ and time $t$ can be derived according to Eqs. (7) and (38) as:

The mean and variance of the stochastic displacement at position $x$ and time $t$ can be respectively obtained as:

where the subscript “$w$” denotes the random displacement of the beam. The mean value and variance of the stochastic velocity and acceleration at position $x$ and time $t$ can also be obtained by substituting the first and second derivatives ${\dot{\mathbf{y}}}_j^{\mathrm{\text{'}}}\left(t\right)$ and ${\ddot{\mathbf{y}}}_j^{\mathrm{\text{'}}}\left(t\right)$ obtained from Eq. (37) into Eq. (40). Samples of the stochastic displacement of the beam structure at position $x$ and time $t$ can be generated from Eq. (39) with any available sampling techniques, e.g. the Latin Hypercube sampling [24], to simulate the Gaussian random variables ${\xi }_i\left(\theta \right)$ in the Polynomial Chaos ${\mathrm{\Psi }}_j\left(\theta \right)$. The probabilistic density function of the stochastic displacement of the beam structure at position $x$ and time $t$ can then be obtained from Eq. (39) after the coefficients ${\mathbf{y}}_j^{\mathrm{\text{'}}}\left(t\right)$ are calculated.

6.1. Coefficients in the one-dimensional Polynomial Chaos expansion

According to the proposed method, the one-dimensional PCE for each uncoupled non-Gaussian random variable should be performed. A numerical study is conducted to compare the efficiency and accuracy of different existing techniques, such as, the Latin Hypercube sampling and the Fitting Regression model proposed by Choi et al. [23]. Considering the two functions $Y_1$ and $Y_2$ including the normal random variable $\xi$ with a zero mean value and unit standard deviation as:

The coefficients in the one-dimensional PCE of the two functions are calculated with different existing techniques and with different order of PC up to four. The relative error and the time required in the calculation of coefficients of PCE using MCS method [21] with 10000 samples, the Latin Hypercube Sampling (LHS) method [22] with 300 samples, and Fitting Regression Model (FRM) method [23] using 300 samples respectively are shown in Table 1. The programme runs on a computer with Intel Core 2, Quad CPU 2.40 Hz and 8 GB RAM. Results show that the Fitting Regression Model method has both high efficiency and accuracy comparing with the other two methods especially for random variables which can be approximated as Polynomial functions of Gaussian random variables. Therefore, this method will be adopted in the following study to calculate the coefficients in the one-dimensional PCE in the reduced PCE model.

6.2. Effect of the level of randomness in system parameters

Different levels of randomness in the system parameters, i.e. different $\mathrm{C}\mathrm{O}{\mathrm{V}}_{\rho }$ and $\mathrm{C}\mathrm{O}{\mathrm{V}}_E$ are investigated. Different orders of Polynomial Chaos are adopted to represent the lognormal random processes of system parameters. To highlight the effect of the level of randomness in system parameters on the accuracy of the non-Gaussian model, the two excitation forces are assumed as deterministic ($\mathrm{C}\mathrm{O}{\mathrm{V}}_F=$ 0%) in this Section as defined in Eqs. (41) and (42).

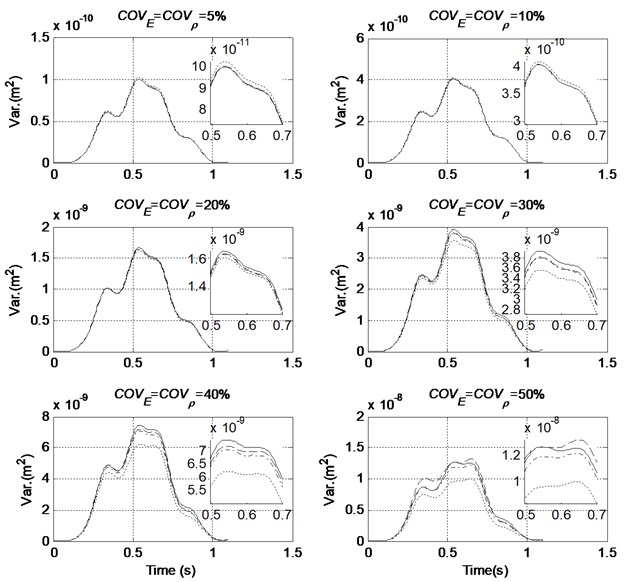
The mean value and variance of the mid-span displacement of the beam structure calculated with the proposed method under different order of PC and the MCS are compared in Figs. 2 and 3, respectively. The detail informations from 0.5 s to 0.7 s are also demonstrated to achieve a better understanding of the results.

The relative errors of the results compared with those from the MCS according to Eq. (43) are listed in Table 2.

Results show that the calculated mean values for all the cases are very accurate and the relative error increases slightly with the increase of level of randomness in system parameters. The order of PC adopted has little effect on the accuracy of calculated mean value in general. For the variance of the mid-span displacement, the use of a low order of PC such as an order of 2, can achieve a high accuracy as noted in Table 2 when the $\mathrm{C}\mathrm{O}{\mathrm{V}}_E$ and $\mathrm{C}\mathrm{O}{\mathrm{V}}_{\rho }$ are small and below 0.2. The results from large COV values can, however, be improved with the use of 3rd and 4th order PC, and the result from a 4th-order representation is better that that from a 3rd-order representation. Large error exists in the calculated variance when only a 2nd-order PCE is adopted for the cases with $\mathrm{C}\mathrm{O}{\mathrm{V}}_E$ and $\mathrm{C}\mathrm{O}{\mathrm{V}}_{\rho }$ larger than 0.2.

Fig. 2Comparison of the mean mid-span displacement with different order of PC (COVF= 0 %, — MCS, ----- Order 2, –·– Order 3, – – Order 4)

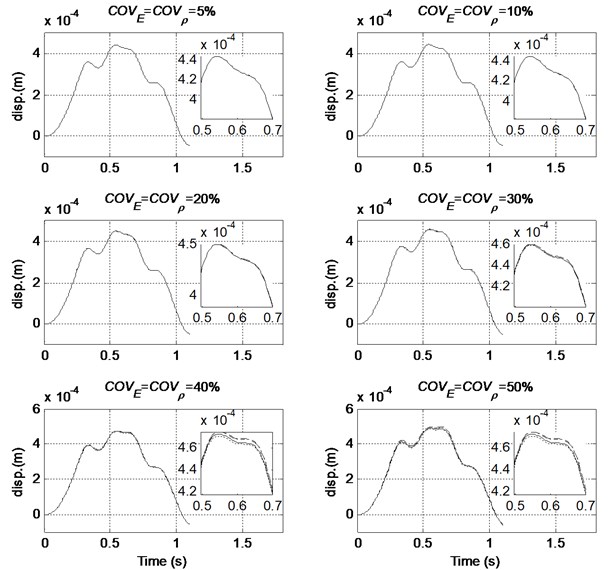
Fig. 3Comparison of variance of mid-span displacement with different order of PC (COVF= 0 %, — MCS, ----- Order 2, –·– Order 3, – – Order 4)

Another observation noted in Table 2 is that for a very large $\mathrm{C}\mathrm{O}{\mathrm{V}}_E$ and $\mathrm{C}\mathrm{O}{\mathrm{V}}_{\rho }$, e.g. larger than 0.4, the mean and variance from a 3rd-order representation are better that that from a 4th-order representation. This phenomenon can be explained as follows: the error in the coefficient calculation from the one-dimensional polynomial chaos expansion will be amplified by the K-L components of the random processes, and it will propagate into the reduced PCE model causing larger errors. It may be concluded that when more coefficients in the one-dimensional PCE are included in the calculation with higher order Polynomial Chaos, the computation error will be amplified and accumulated affecting the accuracy of the calculated response statistics.

Via the comparison of response statistics with the MCS method in Table 2, the accuracy of the proposed method is proved. The proposed method also has good efficiency, for example, in the case when $\mathrm{C}\mathrm{O}{\mathrm{V}}_E=\mathrm{C}\mathrm{O}{\mathrm{V}}_{\rho }=\mathrm{}$20 %, 10 min is required for 10000 runs of MCS to obtain the response statistics and only 15 s is needed for the proposed method.

6.3. Effect of the distance of interest

It is noted that a refined distance between two points in a spatial domain of interest $\left|x_1-x_2\right|$ will increase the number of K-L components in the PCE of a non-Gaussian system parameter. According to Section 5.1, to increase the total number of K-L components in the reduced PCE can improve the accuracy of variance representation of the non-Gaussian parameter. Although the number of the KLE increases in this reduced PCE, yet the total number of Polynomial Chaos adopted under the assumption of “uncoupled” $\left\{{\xi }_i\right(\theta \left)\right\}$ is much smaller than that in a “full” PCE.

Fig. 4Comparison of variance of mid-span displacement with different distance of interest (Order of PC = 3, COVF= 0 %, — MCS, -*- 0.5 m, ----- 1 m, –·– 2.5 m, – – 5 m)

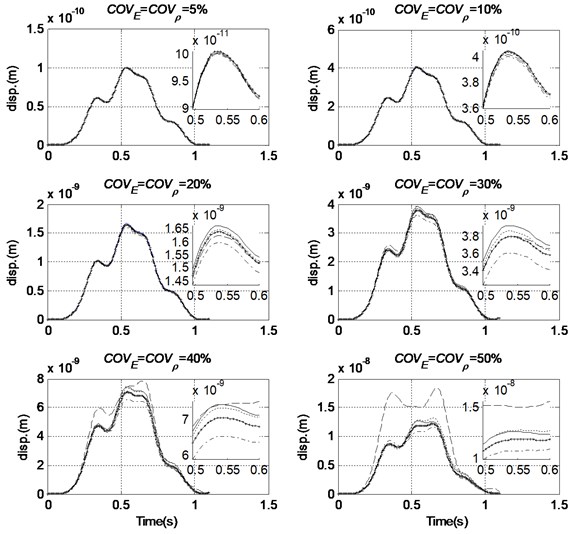
A numerical study is carried out on the moving load on beam system with ${\mathrm{C}\mathrm{O}\mathrm{V}}_F=$0 % and the order of PCE equals to three in this sub-section to show the effect of the distance of interest on the accuracy of the predicted variance of the response. A comparison between the predicted variance of response using MCS and the reduced PCE method with different distance of interest are shown in Fig. 4, and the corresponding relative errors are shown in Table 3. The detail informations from 0.5 s to 0.6 s are also demonstrated in Fig. 4 to achieve a better understanding of the results.

Results show that when the level of randomness in the system parameters is not large, e.g. $\mathrm{C}\mathrm{O}\mathrm{V}\le$ 0.2, with a relative large distance of interest $\left|x_1-x_2\right|=$5.0 m, that is 1/8 of the total length of the beam, the relative error in the predicted variances of the response is less than 4 % indicating a good accuracy. When the level of randomness increase, with $\left|x_1-x_2\right|=$5.0 m, larger error exists in the predicted variance of response. By decreasing the distance of interest, the relative error in the predicted variance of the response can be significantly reduced. For example, when the level of randomness in the system parameters has a $\mathrm{C}\mathrm{O}\mathrm{V}=$0.5, and the distance of interest is decreased from 5.0 m to 1.0 m, the relative error in the predicted variance of response reduced from 57.3 % to 3.68 % according to results in Table 3. The relative error in the predicted variance of response decreases with smaller distance between two points of interest. It is noted from Table 3 that such reduction can be achieved favourably when $\left|x_1-x_2\right|=$1.0 m. Due to the “uncoupled” assumption made in the proposed reduced PCE model, the relative error in the predicted variance of response is not linearly decreasing with the distance of interest.

6.4. Effect of the level of randomness in excitation

Investigations on the effect of the level of randomness in excitation is similarly conducted with ${\mathrm{C}\mathrm{O}\mathrm{V}}_E={\mathrm{C}\mathrm{O}\mathrm{V}}_{\rho }=$20 % in this section. Different levels of randomness of the lognormal distributed excitation forces are adopted with different order in the Polynomial Chaos.

The mean and variance of the mid-span displacement of the beam structure obtained using the proposed method with different order of PCE and from the MCS are compared in Figs. 5 and 6, respectively. The detail informations from 0.5 s to 0.7 s are also demonstrated to achieve a better understanding of the results.The relative errors according to Eq. (43) from both methods are listed in Table 4.

Results show that the order of Polynomial Chaos has little effect on the accuracy of the mean mid-span displacement. When the ${\mathrm{C}\mathrm{O}\mathrm{V}}_F$ are equal or larger than 0.2, a relatively large error exists in the calculated variance from a 2nd-order representation. When the ${\mathrm{C}\mathrm{O}\mathrm{V}}_F$ becomes large, e.g. at 0.4 or 0.5, a 3rd-order representation has better performance than a 4th-order representation. The reason for this phenomenon has been explained in the last paragraph in Section 6.2.

Fig. 5Comparison of mean mid-span displacement with different level of randomness in excitation and different order of PC used (COVE=COVρ= 20 %, — MCS, ----- Order 2, –·– Order 3, – – Order 4)

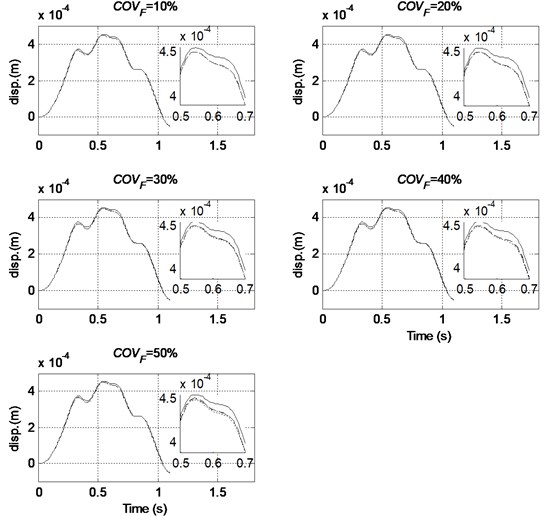
Fig. 6Comparison of variance of mid-span displacement with different level of randomness in excitation and different order of PC used (COVE=COVρ= 20 %, — MCS, ----- Order 2, –·– Order 3, – – Order 4)

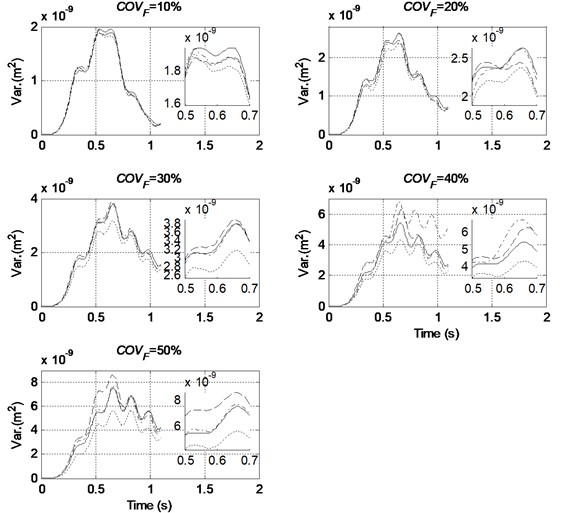
It may be concluded that when a system with the coefficients of variation of both the system parameters and excitation forces smaller than 0.2, a 2nd-order representation of the Polynomial Chaos should be sufficient to obtain accurate response statistics of the system. In other cases with larger coefficients of variation, a 3rd-order representation of Polynomial Chaos is recommended. When the coefficient of variation of the excitation forces attains a large value of 0.5, the response statistics of the non-Gaussian model with a reduced PCE could still maintain a good accuracy.