Bending of inhomogeneous sandwich plates with viscoelastic cores

1. Introduction

Sandwich structure is widely used in modern applications, especially in civil, marine and mechanical engineering industries due to its light weight and high rigidity. Sandwich plates are basically a special form of fiber-reinforced rectangular plates composed of alternative arrangement of thin stiff layers and thick flexible cores. They also made up of two thin strong, stiff face layers which resist bending bonded to a relatively thicker, less dense core layer to resist shear force. There has recently been a great interest to study the behavior of sandwich structures subjected to static or dynamic loads [1-4]. Whitney [5] and Vinson [6] have discussed the structure of sandwich plates and emphasized the importance of including shear flexibility of their cores. Pagano [7] and Pagano and Hatfield [8] have presented exact 3-D elasticity solutions for the stresses in the composite laminates and sandwich plates. In fact, Zenkour [9] has presented recent results more general than the well-known of Pagano [7] and Pagano and Hatfield [8] and they served as benchmark solutions for other researchers. Zenkour and his colleagues [10-15] have presented a 2-D solution for the bending and/or free vibration of functionally graded (FG) sandwich rectangular plates. They have investigated the thermo-mechanical bending analysis of FG sandwich plates. In addition, they have presented much elastic foundation analyses of uniformly loaded FG viscoelastic sandwich plates.

The classical plate theory (CPT) gives inaccurate results for thick or may be moderately thick rectangular plates because it ignores transverse shear effects. However, it provides reasonable results for thin plates. The first-order shear deformation plate theory (FPT) [16] is an improvement on the CPT. It accounts for transverse shear effects but needs a shear correction factor to give reasonable results. Higher-order shear deformation plate theory (HPT) [17] can represent the kinematics behavior of most laminated plates better. It does not require shear correction factors and can be used to compute inter-laminar stresses more accurately.

In this article, the sinusoidal shear deformation theory of plate (SPT) [18] as well as other familiar plate theories (CPT, FPT and HPT) is used to study the static bending of a viscoelastic rectangular sandwich plate. The faces of this sandwich plate made of the same elastic isotropic material while its core is made of a viscoelastic one. With the help of Illyushin approximation method [19], and the effective-moduli method [20], a wide range of deflections and stresses is presented to the bending of sandwich plates. A comparison between the various theories of plates is investigated. Additional results for the bending of fiber-reinforced inhomogeneous viscoelastic sandwich plates are added to serve as benchmarks for future comparisons with other researchers.

2. Basic equations

Let us consider a symmetric sandwich plate of uniform thickness $h$, length $a$, and width $b$ and composed of three inhomogeneous layers (see Fig. 1). To describe infinitesimal deformations of the three-layer sandwich plate one can used the Cartesian coordinates $(x,y,z)$. The plane $z=\text{0}$ represents the mid-plane of the plate while $z=\pm h/2$ represent its external bounding planes. The upper surface is subjected to a normal traction ${\sigma }_z=-q(x,y)$, while its lower surface is traction free. Different types of symmetric sandwich plate are considered according to the thickness of the core and faces. For example, the (1-5-1) sandwich plate is given when the core thickness of the plate is equal to five times the face thickness, i.e., $h_1=-5h/14$ and $h_2=+5h/14$. In the (2-1-2) sandwich plate, the core thickness is half the face thickness, i.e., $h_1=-h/10$ and $h_2=+h/10$. The (1-1-1) sandwich plate is made of three layers with equal thickness, i.e., $h_1=-h/6$ and $h_2=+h/6$. Also, the coreless sandwich plate (1-0-1) is considered with two face layers of equal thickness, i.e., $h_1=h_2=0$.

Fig. 1Coordinates and geometry for the viscoelastic sandwich plate

The material properties of the inhomogeneous layers are smoothly varying in the thickness $z$-direction only. That is:

where $n$ is the inhomogeneity parameter and ${\stackrel{-}{c}}_{ij}^{\left(k\right)}$ are the transformation elastic coefficients that depending on the material properties of the homogeneous $k$th layer:

in which $E_k$ is Young’s modulus of layer $k$ and ${\nu }_k$ is its Poisson’s ratio. The displacement field of a point at $(x,y,z)$ in the plate may be written as [18]:

where $(V_1,V_2,V_3)$ are functions of the spatial co-ordinate that represent the displacements corresponding to the co-ordinate system; $(u_1,u_2,u_3)$ are the displacements along the axes $x$, $y$ and $z$, respectively, and $u_4$ and $u_5$ are the rotations about the $x$- and $y$-axes. The generalized displacements $u_i$ are functions of $x$ and $y$. The shape function $\psi \left(z\right)$ may be chosen such that:

The first condition in Eq. (4) means that the transverse shear strain vanishes on the bounding planes $z=\pm h/2$. The shear deformation theory that satisfies this condition dose not requires any shear-correction factors. In general, the second condition in Eq. (4) may be satisfied for most two-dimensional theories. In more details, there is no shape function for CPT, i.e. $\psi \left(z\right)=0$ while $\psi \left(z\right)=z$ for FPT, $\psi \left(z\right)=z\left[1-\frac{4}{3}{\left(\frac{z}{h}\right)}^2\right]$ for HPT, and $\psi \left(z\right)=h/\pi \sin \left(\pi z/h\right)$ for SPT [20].

The strain-displacement relations are given by:

where:

Each layer of the present sandwich plate may be treated as an individual inhomogeneous plate. So, the stress-strain relations for the $k$th layer, according to the inclusion of the transverse shear deformation, can be expressed as:

The principle of virtual displacement may be expressed for this case as:

or:

where $N_i$ are the stress resultants, $M_i$ are the stress couples, $Q_j$ are the transverse shear stress resultants, and $S_i$ are stress couples added to associate with the transverse shear effects:

in which $h_{k-1}$ and $h_k$ are the bottom and top $z$-coordinates of the layer $k$.

3. Governing equations

Eq. (8) is used to obtain the governing equilibrium equations by integrating the displacement gradient in ${\epsilon }_i$ by parts and setting the coefficients of $\delta u_i$ to zero separately. In this case, we get:

Substituting Eq. (7) into Eq. (10), the resultants $N_i$, $M_i$, $Q_j$ and $S_i$ can be represented in terms of the total strains:

where:

The stiffness coefficients $A_{ij}$, $B_{ij}$, … etc., are defined as:

where $K_4$ and $K_5$ represent the shear correction factors for FPT only. Their suitable values for FPT are $K_4=K_5=\text{5/6}$. Otherwise, they should be unity.

4. Closed-form solution

The closed-form solution of Eq. (11) for the sandwich plate may be obtained here. The simply-supported boundary conditions at the side edges are imposed as follows:

To solve the present problem, the external force is represented according to Navier-type in the form of a sinusoidally distributed load as:

where $\lambda =\pi /a$ and $\mu =\pi /b$. The plate-center intensity of the load is denoted by $q_0$. In addition, one can assume the following solution forms for $u_i$ that satisfies the boundary conditions:

where $U_i$ are arbitrary parameters to be determined. Substituting Eqs. (16) and (17) into Eq. (11), one obtains:

where $\left\{\mathrm{\Delta }\right\}$ and $\left\{F\right\}$ denote the columns:

where “$T$” denotes the vector transpose of $\left\{F\right\}$ and $\left\{\mathrm{\Delta }\right\}$. The elements $C_{ij}=C_{ji}$ of the coefficient matrix $\left[C\right]$ are given by:

The stress components may be obtained by substituting Eq. (17) into Eq. (6). They are appeared in terms of the arbitrary parameters $U_i$ and the material properties as:

5. Viscoelastic solution

In this problem, the core is made of a viscoelastic isotropic material while the face sheets are made of an isotropic material with $E_1=E_3=E$ and ${\nu }_1={\nu }_3=\nu$. However, the viscoelastic properties are given by:

where $K$ is the bulk modulus (the coefficient of volume compression) and $\stackrel{-}{\omega }$ is the dimensionless kernel of relaxation function. It is assumed that $K$ is not relaxed, i.e. $K=$ constant.

Firstly, the corresponding elastic problem is solved numerically for variable values of $\stackrel{-}{\omega }$. Then, one can use the realization method of elastic solution for solving the problem of quasi-static linear viscoelastic composite. In the elastic case $u_i$ are functions of $x$, $y$ and $\stackrel{-}{\omega }$ while in the viscoelastic case, they are operator functions of $x$, $y$ and time $t$. According to Illyushin’s approximation method (see Pobedrya [19]), the displacement functions $u_i$ can be represented for layer $k$ in the form:

where ${\mathrm{\Phi }}_j\left(\stackrel{-}{\omega }\right)$ are five known kernels. They constructed on the basis of $\stackrel{-}{\omega }$ and one can choose them in the form:

where ${\stackrel{-}{g}}_{{\beta }_2}=1/1+{\beta }_m\stackrel{-}{\omega }$, $m=\text{1, 2}$. The coefficients $A_{ij}^{\left(k\right)}\left(x,y\right)$ may be determined from the following algebraic equations system:

where:

The viscoelastic solution can now record to get explicit unified form for the displacements $u_i^{\left(k\right)}\left(x,y,t\right)$ as:

Taking $q_0\left(t\right)={\stackrel{-}{q}}_{0}H\left(t\right)$ where $H\left(t\right)$ is the Heaviside’s unit step function:

then, Eq. (27) for the two problems takes the form:

where $\omega \left(t\right)\equiv \stackrel{-}{\omega }$, $\pi \left(t\right)\equiv \stackrel{-}{\pi }$, and $g_{{\beta }_m}\left(t\right)\equiv {\stackrel{-}{g}}_{{\beta }_m}$.

Assuming an exponential relaxation function:

where $c_1$ and $c_2$ are constants, $\alpha =1/t_s$ and $t_s$ is the relaxation time. The functions $\pi \left(t\right)$ and $g_{{\beta }_m}\left(t\right)$ can be determined by deducing their Laplace-Carson transforms from the known ones of $\omega \left(t\right)$ [21, 22]. They take the following forms:

where:

So, the displacements are given in the final form, in terms of the time $t$ or the time parameter $\tau$, by:

Once again, the same technique is used to obtain the stresses by replacing only $u_i^{\left(k\right)}\left(x,y,t\right)$ with ${\stackrel{-}{\sigma }}_i^{\left(k\right)}\left(x,y,z,t\right)$. So, the bending stresses in terms of the time $t$ or the time parameter $\tau$ are given by:

6. Numerical examples and discussions

Numerical examples are obtained for the deflections of and stresses in viscoelastic sandwich plates. The relaxation time $\alpha$ is still unknown and the time parameter $\tau =\alpha t$ is given in terms of it. The constitutive parameter is given by $\zeta =E/K$. In addition, it is assumed, unless otherwise stated, that $\nu =\text{0.3}$, $b=\text{3}a$, $\zeta =\text{0.2}$, $a=\text{10}h$, $n=\text{4}$, $c_1=\text{0.1}$, and $c_2=\text{0.9}$.

The following dimensionless quantities are used throughout the calculations ($Z=z/h)$:

Table 1 contains the dimensionless deflections $w$ of inhomogeneous (1-5-1) viscoelastic sandwich plates. The effect of the side-to-thickness ratio $a/h$, the constitutive parameter $\zeta$, and the aspect ratio $b/a$ is presented. The results show that the dimensionless deflection $w$ increases as the side-to-thickness ratio $a/h$ and aspect ratio $b/a$ increase while it decreases as the constitutive parameter $\zeta$ increases. The HPT yields results closer than FPT to those obtained using SPT. The CPT failed to give reliable results for thicker plates $\text{(}a/h=\text{5)}$.

Tables 2-4 contain the stresses in the inhomogeneous (1-5-1) viscoelastic sandwich plates at different values of side-to-thickness ratio $a/h$, constitutive parameter $\zeta$ and aspect ratio $b/a$, respectively. The results given in Table 2 show that the stresses, except ${\sigma }_6$, increase as the side-to-thickness ratio $a/h$ increases. Table 3 shows that the stresses ${\sigma }_1$ and ${\sigma }_6$ increase with the increase of $\zeta$ while the rest of stresses are decreasing. Table 4 shows that the stresses increase with the increase of the aspect ratio $b/a$. In these figures, CPT gives similar results as FPT and may be ignore. Once again, HPT yields results closer than FPT to those obtained using SPT.

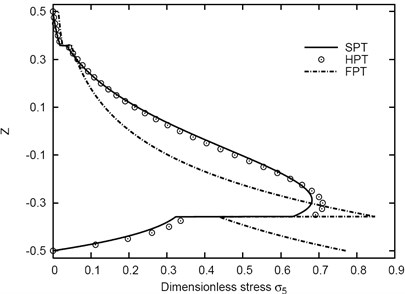
Figs. 2 and 3 illustrate the transverse shear stresses ${\sigma }_4$ and ${\sigma }_5$ through-the-thickness of the (1-5-1) sandwich plate using various theories. It can be seen that the shear stresses take larger values at the core (viscoelastic) layer and the HPT yields results very close to those obtained using SPT. The FPT gives non-zero shear stresses at the top and bottom surfaces of the plate. Also, the SPT gives accurate results, especially transverse shear stresses, compared with other theories including HPT. This is an expected because SPT is the generalized one.

In Figs. 4 and 5, the SPT is used to plot the shear stresses ${\sigma }_4$ and ${\sigma }_5$ through-the-thickness of different kinds of the sandwich plates. It is seen that, both of ${\sigma }_4$ and ${\sigma }_5$ take different behaviors according to the thickness of the core layer compared with the thickness of the other faces. If there is no core as in the case of (1-0-1) plate, this means that the plate becomes fully elastic and the shear stresses take the same curve-related shape with maximum points near the lower faces. For other sandwich plates, the maximum values of the shear stresses occur at the first interface. The values of ${\sigma }_5$ may be three times those of ${\sigma }_4$.

Fig. 2Distribution of σ4 through-the-thickness of the (1-5-1) sandwich plate

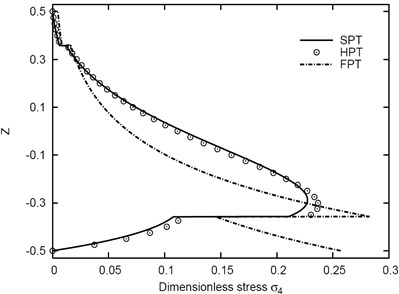
Fig. 3Distribution of σ5 through-the-thickness of the (1-5-1) sandwich plate

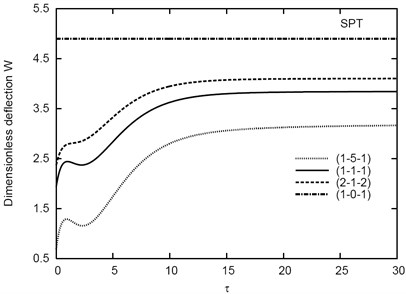
Figs. 6-8 plot the deflection $w$ vs the time parameter $\tau$ of the inhomogeneous (1-5-1) sandwich plate using various theories for different values of aspect ratio $b/a$, side-to-thickness ratio $a/h$, and the constitutive parameter $\zeta$, respectively. It is seen that $w$ increases as $b/a$ and $a/h$ increase and decreases as $\zeta$ increases (see also Table 1). In addition, $w$ increases to get its local maximum at $\tau \cong \text{1}$, then it decreases to get its local minimum at $\tau \cong \text{2.3}$. After that the deflection is directly increasing as the time parameter $\tau$ increases and become constant at $\tau >\text{15}$.

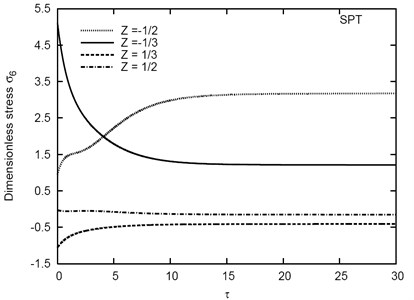
Fig. 9 illustrates the variation of $w$ vs the time parameter $\tau$ for different types of inhomogeneous viscoelastic sandwich plates. It can be seen that, the deflection increases with the decrease of the thickness of the core compared with the thickness of the two faces. The deflection becomes constant in the case of the (1-0-1) fully elastic plate. This is expected since there is no viscoelastic fore for this plate. Finally, Figs. 10-12 illustrate the variation of in-plane stresses ${\sigma }_1$, ${\sigma }_2$, and ${\sigma }_6$ vs $\tau$ for different values of thickness $Z$ of the (1-5-1) sandwich plates. The variations of stresses are appears clearly with the variation of the time parameter $\tau$ and becomes constant for $\tau >\text{12}$.

Fig. 4Distribution of σ4 through-the-thickness of different sandwich plates

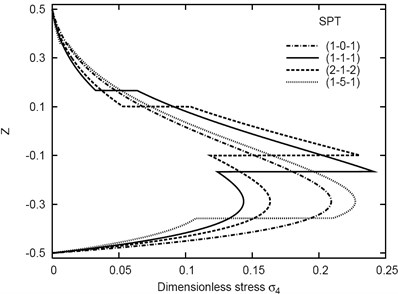
Fig. 5Distribution of σ5 through-the-thickness of different sandwich plates

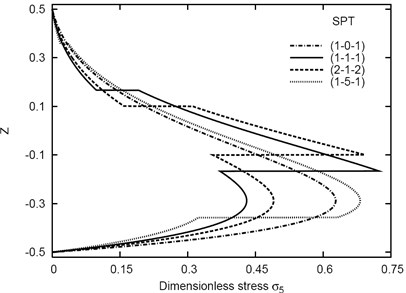
Fig. 6Variation of w vs τ for different b/a of the (1-5-1) sandwich plate

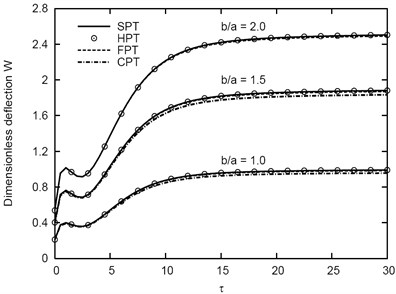
Fig. 7Variation of w vs τ for different a/h of the (1-5-1) sandwich plate

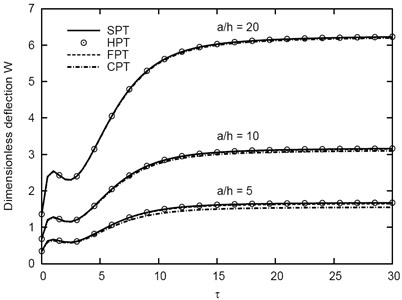
Fig. 8Variation of w vs τ for different ζ of the (1-5-1) sandwich plate

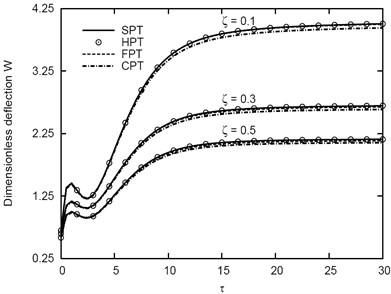
Fig. 9Variation of w vs τ for different sandwich plates

7. Conclusions

Bending response of inhomogeneous viscoelastic sandwich plates is investigated by using various plate theories. The governing equations of the sinusoidal (SPT), higher-order (HPT), first-order (FPT) and classical (CPT) plate theories are converted into a single system of equations. Analytical solutions are developed using the Navier’s procedure and separation of variable technique. The results of SPT are compared with those obtained by HPT, FPT and CPT. The SPT and HPT contain the same number of dependent variables as in FPT, but results are more accurate prediction of deflections and stresses, and satisfy the zero tangential traction boundary conditions on the surfaces of the plate. However, both SPT and HPT do not require the use of shear correction factors. Numerical computations were carried out to study the effect of time parameter $\tau$ on deflections and stresses at different values of aspect ratio $b/a$, side-to-thickness ratio $a/h$ and constitutive parameter $\zeta$. The obtained results show how the dimensionless stresses and deflection affected with the elastic properties of the layers. It is to be noted that, the variation of dimensionless stresses and deflection versus the time parameter has the high sensitivity at viscoelastic layer. The CPT yields identical stresses with the FPT. In conclusion, the HPT yields results very close to those obtained using SPT which gives accurate results, especially transverse shear stresses, than other theories including HPT.

Fig. 10Variation of σ1 vs τ for different Z in the (1-5-1) sandwich plate

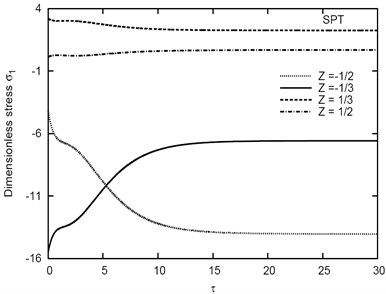
Fig. 11Variation of σ2 vs τ for different Z in the (1-5-1) sandwich plate

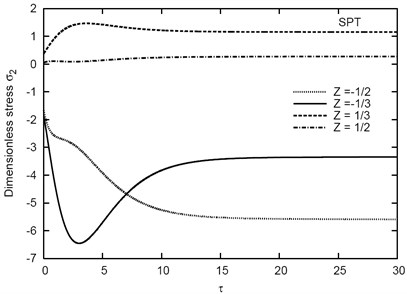
Fig. 12Variation of σ6 vs τ for different Z in the (1-5-1) sandwich plate