Three dimensional wave propagation in axially loaded pressurized FG cylindrical shells using Frobenius power series and Rayleigh-Ritz methods

Adnani, Amir Ali Tabatabai; Talebitooti, Roohollah; Morovati, Mehdi

Journal of Vibroengineering

Browse Journal

Submit article

Published: 15 May 2015

Check for updates

Three dimensional wave propagation in axially loaded pressurized FG cylindrical shells using Frobenius power series and Rayleigh-Ritz methods

Amir Ali Tabatabai Adnani¹

Roohollah Talebitooti²

Mehdi Morovati³

¹Mathematics Department, Islamic Azad University, Central Tehran Branch, Tehran, Iran

²School of Mechanical Engineering, Iran University of Science and Technology, Tehran, Iran

³Young Researches and Elite Club, Central Tehran Branch, Islamic Azad University, Tehran, Iran

Corresponding Author:

Amir Ali Tabatabai Adnani

Cite the article Download PDF

Downloads 1166

Abstract

In the present study, the behavior of vibratory cylindrical shells composed of functionally graded material (FGM) containing copper and tungsten under internal pressure and axial compression loads is investigated. An exact solution of free harmonic wave propagation using the theory of three dimensional elasticity is extracted. Then, the dispersion equation is analyzed in conjunction with a Frobenius power series method and natural frequency (eigenvalue) of the shell is obtained using Rayleigh-Ritz method. Furthermore, the present analysis is validated by comparing results with those available in the literature.

1. Introduction

A Functionally Graded Material (FGM) is a material whose composition is changed over volume to perform a certain function(s). Thus, the material properties including chemical, mechanical, thermal, and electrical properties depend on the spatial position in the structure. FGM materials provide opportunities to take the benefits of different material systems. Multi-functionality, ability to control deformation, dynamic response, wear, corrosion as well as the ability to remove stress concentrations are the main advantages of these materials.

During recent years, FGM cylindrical shells are come into considered by many researches from different cases. Z. S. Shao [1] carried out Three-dimensional thermo-elastic analysis of a functionally graded cylindrical panel with finite length and subjected to non-uniform mechanical and steady-state thermal loads. They assumed thermal and mechanical properties of the functionally graded material to be temperature independent and continuously vary in the radial direction of the panel. P. Malekzadeh et al. [2] studied the three-dimensional (3D) free vibration of laminated cylindrical panels with finite length and functionally graded (FG) layers. K. Daneshjou et al. [3] presented an analytical solution for acoustic transmission through relatively thick FGM cylindrical shells using third order shear deformation theory (TSDT). G. G. Sheng et al. [4] presented an analytical method based on Hamilton’s principle, Von Kármán non-linear theory and the first-order shear deformation theory, to investigate the FG (functionally graded) cylindrical shells subjected to thermal and axial loads. Guoyong Jin et al. [5] presented a simple yet efficient solution approach based on the Haar wavelet using the first-order shear deformation shell theory to investigate the free vibration analysis of FG cylindrical shell. M. J. Ebrahimi et al. [6] analyzed free vibration of a two-dimensional functionally graded circular cylindrical shell. They derived the equations of motion based on the Love’s first approximation classical shell theory. M. Asgari et al. [7] investigated natural frequencies characteristics of a thick hollow cylinder with finite length made of two dimensional FGM based on three-dimensional equations of elasticity. M. Shakeri et al. [8] studied the analysis of functionally graded thick hollow cylinders under dynamic load. S. M. Hasheminejad et al. [9] investigated the steady-state non-axisymmetric sound radiation characteristics of an arbitrarily thick functionally graded hollow cylinder of infinite length subjected to arbitrary time-harmonic on-surface concentrated mechanical drives by employing the linear three-dimensional elasticity theory in conjunction with the powerful transfer matrix solution technique. S. M. Hosseini [10] calculated the velocity of elastic wave propagation in functionally graded materials (FGMs) by using a hybrid mesh-free method based on generalized finite difference (GFD) and Newmark finite difference (NFD) methods. G. Taj M. N. A. et al. [11] investigated the dynamic response of functionally graded skew shell using $C_{0}$ finite element formulation. In continue, they applied Reddy’s higher order theory to perform the analysis. Also, their studies focus mainly on the influence of skew angle on frequency parameter and displacement of shell panel with various geometrics. In addition to the literature reviewed above, many researches used the Rayleigh-Ritz method to predict the natural frequency of the system. K. K. Pradhan et al. [12] used Rayleigh-Ritz method to extract governing equations of system. They also analyzed free vibration of FG beams subjected to different sets of boundary conditions. Their analysis was based on the classical and first order shear deformation beam theories. S. Sun et al. [13] employed the Rayleigh-Ritz method to derive the frequency equations of rotating cylinders with classical homogeneous boundary conditions. They also utilized artificial springs to simulate the elastic constraints imposed on the cylinders’ edges. In other word, they derive the frequency equations of rotating cylindrical shells with more general boundary conditions by considering the strain energy of artificial springs during the Rayleigh-Ritz procedure. M. Biglar et al. [14] applied the Rayleigh-Ritz method for deriving dynamic modeling of cylindrical shell and piezoelectric sensors and actuators based on the Donnel-Mushtari shell theory. G. Jin et al. [15] obtained an exact solution based on Rayleigh-Ritz procedure by the energy functions of the plate since the displacement fields were constructed adequately smooth throughout the entire solution domain. Most of analytical studies surveyed above, have not considered 3D wave propagation in their works. Furthermore, in a few one which consider the 3D wave propagation, the effectes of internal pressure and axial load are completely ignored.

In this paper, the behavior of cylindrical shell consists of two different functionally graded material (copper and tungsten) is studied using three dimensional elasticity theory. The governing equations of motion are analyzed with the aid of Frobeninus power series method. Then, the natural frequency of the system is obtained using Rayleigh-Ritz method. In addition, the buckling loads due to axial compression on the cylindrical shell for both copper and tungsten FG material are discussed. Finally, the presented results compared with those of other authors, indicte the good accuracy of the presented work.

2. Governing equations of the system

A cylindrical shell with a radius $r$ , length $L$ and thickness $h$ is considered. The isotropic material is employed with one plane of symmetry. The displacement filed is expressed in the cylindrical coordinates system as follows:

1

u_{r} = u_{r} (r, θ, z, t), u_{θ} = u_{θ} (r, θ, z, t), w = w (r, θ, z, t),

where $u_{r}$ , $u_{θ}$ , $w$ , $t$ are the components of the radial, circumferential, axial displacements and time, respectively. The generalized Hooke’s law in each layer of the shell can be written as follows [16]:

2

[\begin{array}{l} σ_{r} \\ σ_{θ} \\ σ_{z} \end{array}] = (\begin{matrix} C_{11} & C_{12} & 0 \\ C_{12} & C_{22} & 0 \\ 0 & 0 & C_{33} \end{matrix}) [\begin{array}{l} ε_{r} \\ ε_{θ} \\ ε_{z} \end{array}], [\begin{array}{l} τ_{θ z} \\ τ_{r z} \\ τ_{r θ} \end{array}] = (\begin{matrix} C_{44} & C_{45} & 0 \\ C_{45} & C_{55} & 0 \\ 0 & 0 & C_{66} \end{matrix}) [\begin{array}{l} γ_{θ z} \\ γ_{r z} \\ γ_{r θ} \end{array}],

where $σ_{r}$ , $σ_{θ}$ , $σ_{z}$ are stresses, $ε_{r}$ , $ε_{θ}$ , $ε_{z}$ are strains, $τ_{θ z}$ , $τ_{r z}$ , $τ_{r θ}$ are shear stresses and finally $γ_{θ z}$ , $γ_{r z}$ , $γ_{r θ}$ are shear strains. In adittion, each matrix elements in Eq. (2) are defined as follows:

3

C_{11} = C_{22} = \frac{E h}{1 - υ^{2}}, C_{12} = C_{21} = \frac{E h υ}{1 - υ^{2}}, C_{33} = \frac{E h (1 - υ)}{2 (1 - υ^{2})},

C_{44} = C_{55} = \frac{E h^{3}}{12 (1 - υ^{2})}, C_{45} = C_{54} = \frac{E h^{3} υ}{12 (1 - υ^{2})}, C_{66} = \frac{E h^{3} (1 - υ)}{24 (1 - υ^{2})},

where $E$ , $υ$ and $h$ are Young’s modulus, Poisson’s ratio and shell thickness, respectively. Also, the engineering strain-displacement relation can be expressed as:

4

ε_{r} = \frac{\partial u_{r}}{\partial r}, ε_{θ} = \frac{1}{r} \frac{\partial u_{θ}}{\partial θ} + \frac{u_{r}}{r}, ε_{z} = \frac{\partial w}{\partial z}, γ_{θ z} = \frac{1}{r} \frac{\partial w}{\partial θ} + \frac{\partial u_{θ}}{\partial z},

γ_{r z} = \frac{\partial w}{\partial r} + \frac{\partial u_{r}}{\partial z}, γ_{r θ} = \frac{1}{r} \frac{\partial u_{r}}{\partial θ} + r \frac{\partial}{\partial r} (\frac{u_{θ}}{r}) = \frac{1}{r} \frac{\partial u_{r}}{\partial θ} - \frac{u_{θ}}{r} + \frac{\partial u_{θ}}{\partial r} .

The equilibrium equations for a cylindrical shell subjected to internal pressure and axial compression loads in a cylindrical coordinate system can be written as follows:

5a

\frac{\partial σ_{r}}{\partial r} + \frac{1}{r} \frac{\partial τ_{r θ}}{\partial θ} + \frac{\partial τ_{r z}}{\partial z} + \frac{σ_{r} - σ_{θ}}{r} = ρ \frac{\partial^{2} u_{r}}{\partial t^{2}},

5b

\frac{\partial τ_{r θ}}{\partial r} + \frac{1}{r} \frac{\partial σ_{θ}}{\partial θ} + \frac{\partial τ_{θ z}}{\partial z} + \frac{2 τ_{r θ}}{r} + σ_{θ} = ρ \frac{\partial^{2} u_{θ}}{\partial r^{2}},

5c

\frac{\partial τ_{r z}}{\partial r} + \frac{1}{r} \frac{\partial τ_{θ z}}{\partial θ} + \frac{\partial σ_{z}}{\partial z} + \frac{τ_{r z}}{r} + σ_{z} = ρ \frac{\partial^{2} w}{\partial t^{2}},

where $r$ and $ρ$ are shell radius and density of the materials, respectively. Substitution of Eqs. (1), (2) and (4) into Eqs. (5a)-(5c) leads to the following displacement equations of motion as follows:

6a

u_{r} \{C_{11} \frac{\partial^{2}}{\partial r^{2}} + C_{11} \frac{1}{r} \frac{\partial}{\partial r} + C_{66} \frac{1}{r^{2}} \frac{\partial^{2}}{\partial θ^{2}} + C_{55} \frac{\partial^{2}}{\partial z^{2}} - C_{22} \frac{1}{r^{2}}\}

+ u_{θ} \{C_{12} \frac{1}{r} \frac{\partial^{2}}{\partial r \partial θ} - C_{66} \frac{1}{r^{2}} \frac{\partial}{\partial θ} + C_{66} \frac{1}{r} \frac{\partial^{2}}{\partial r \partial θ} + C_{45} \frac{\partial^{2}}{\partial z^{2}} + C_{12} \frac{1}{r^{2}} \frac{\partial}{\partial θ} - C_{22} \frac{1}{r^{2}} \frac{\partial}{\partial θ}\}

+ w \{C_{45} \frac{1}{r} \frac{\partial^{2}}{\partial θ \partial z} + C_{55} \frac{\partial^{2}}{\partial r \partial z}\} = ρ \frac{\partial^{2} u_{r}}{\partial t^{2}},

6b

u_{r} \{C_{66} \frac{1}{r} \frac{\partial^{2}}{\partial r \partial θ} + C_{12} \frac{1}{r} \frac{\partial^{2}}{\partial r \partial θ} + C_{22} \frac{1}{r^{2}} \frac{\partial}{\partial θ} + C_{45} \frac{\partial^{2}}{\partial z^{2}} + C_{66} \frac{2}{r^{2}} \frac{\partial}{\partial θ} + C_{12} \frac{\partial}{\partial r} + C_{22} \frac{1}{r}\}

+ u_{θ} \{- C_{66} \frac{1}{r^{2}} + C_{66} \frac{1}{r} \frac{\partial}{\partial r} + C_{66} \frac{\partial^{2}}{\partial r^{2}} + C_{22} \frac{1}{r^{2}} \frac{\partial^{2}}{\partial θ^{2}} + C_{44} \frac{\partial^{2}}{\partial z^{2}} + C_{22} \frac{1}{r} \frac{\partial}{\partial θ}\}

+ w \{C_{44} \frac{1}{r} \frac{\partial^{2}}{\partial θ \partial z} + C_{45} \frac{\partial^{2}}{\partial r \partial z}\} = ρ \frac{\partial^{2} u_{θ}}{\partial t^{2}},

6c

u_{r} \{C_{55} \frac{\partial^{2}}{\partial r \partial z} + C_{45} \frac{1}{r} \frac{\partial^{2}}{\partial θ \partial z} + C_{55} \frac{1}{r} \frac{\partial}{\partial z}\} + u_{θ} \{C_{45} \frac{\partial^{2}}{\partial r \partial z} + C_{44} \frac{1}{r} \frac{\partial^{2}}{\partial θ \partial z} + C_{45} \frac{1}{r} \frac{\partial}{\partial z}\}

+ w \{C_{45} \frac{1}{r} \frac{\partial^{2}}{\partial r \partial θ} + C_{55} \frac{\partial^{2}}{\partial r^{2}} + C_{44} \frac{1}{r^{2}} \frac{\partial^{2}}{\partial θ^{2}} + C_{45} \frac{1}{r} \frac{\partial^{2}}{\partial r \partial θ} + C_{33} \frac{\partial^{2}}{\partial z^{2}} + C_{45} \frac{1}{r^{2}} \frac{\partial}{\partial θ}

{+ C}_{55} \frac{1}{r} \frac{\partial}{\partial r} + C_{33} \frac{\partial}{\partial z}\} = ρ \frac{\partial^{2} w}{\partial t^{2}} .

It is assumed that the propagation of free harmonic waves with three components of wave propagation have a solution formed as follows:

7

u_{r} = U (r) s i n (n θ + ζ z + ω t),

u_{θ} = V (r) c o s (n θ + ζ z + ω t),

w = W (r) c o s (n θ + ζ z + ω t),

where $n =$ 1, 2, 3... is the integer number of waves around the circumference and the wavenumber $ζ = π / l$ is defined as the number of waves over $2 π$ in the axial direction and also, $ω$ is the natural frequency of the waves. The solution for $U (r)$ , $V (r)$ , $W (r)$ can be obtained using a Frobenius power series method which is defined as follows:

8

[U (r), V (r), W (r)] = \sum_{k = 0}^{\infty} [u_{k}, v_{k}, w_{k}] r^{k + λ},

where in Eq. (8) $λ$ is the characteristic parameter that should be determined. The amounts of $u_{0}$ , $v_{0}$ , $w_{0}$ are assumed not equal to zero. Substitution of the solution from Eqs. (7) and (8) into the displacement differential Eqs. (6a)-(6c) yields the following equations:

9a

(C_{11} λ^{2} - C_{66} n^{2} - C_{22}) u_{0} + (- C_{12} n λ + C_{66} n - C_{66} n λ - C_{12} n + C_{22} n) v_{0} = 0,

9b

(C_{66} n λ + C_{12} n λ + C_{22} n) u_{0} + (- C_{66} + C_{66} λ^{2} - C_{22} n^{2}) v_{0} = 0,

9c

(- C_{45} n + C_{55} λ^{2} - C_{44} n^{2}) w_{0} = 0 .

In order to determine the characteristic parameter of the system, the determinant of coefficients in Eqs. (9a)-(9c) should set to zero. Therefore, the generated matrix is:

10

|\begin{matrix} C_{11} λ^{2} - C_{66} n^{2} - C_{22} & n (- C_{12} λ + C_{66} - C_{66} λ - C_{12} + C_{22}) & 0 \\ n (C_{66} λ + C_{12} λ + C_{22} & - C_{66} + C_{66} λ^{2} - C_{22} n^{2} & 0 \\ 0 & 0 & n (- C_{45} - C_{44} n) + C_{55} λ^{2} \end{matrix}| = 0 .

The above determinant results into the following polynomial equation:

11

a_{1} λ^{6} + a_{2} λ^{4} + a_{3} λ^{3} + a_{4} λ^{2} + a_{5} λ + a_{6} = 0,

where $a_{i}$ ; $i =$ 1, 2,..., 6 are the coefficients of Eq. (11) obtained as follows:

a_{1} = C_{11} C_{55} C_{66},

a_{2} = C_{12}^{2} C_{55} n^{2} - C_{11} C_{55} C_{66} - C_{22} C_{55} C_{66} - C_{11} C_{22} C_{55} n^{2} - C_{11} C_{44} C_{66} n^{2}

+ 2 C_{12} C_{55} C_{66} n^{2} - C_{11} C_{45} C_{66} n,

a_{3} = C_{12}^{2} C_{55} n^{2} - C_{55} C_{66}^{2} n^{2},

a_{4} = - C_{12}^{2} C_{44} n^{4} - C_{12}^{2} C_{45} n^{3} + C_{55} C_{66}^{2} n^{2} + C_{22} C_{55} C_{66} + C_{11} C_{22} C_{44} n^{4} + C_{11} C_{22} C_{45} n^{3}

+ C_{12} C_{22} C_{55} n^{2} + C_{11} C_{44} C_{66} n^{2} - 2 C_{12} C_{44} C_{66} n^{4} - 2 C_{12} C_{45} C_{66} n^{3} + C_{22} C_{44} C_{66} n^{2}

- C_{22} C_{55} C_{66} n^{2} + C_{22} C_{55} C_{66} n^{4} + C_{11} C_{45} C_{66} n + C_{22} C_{45} C_{66} n,

a_{5} = - C_{12}^{2} C_{44} n^{4} - C_{12}^{2} C_{45} n^{3} + C_{44} C_{66}^{2} n^{4} + C_{45} C_{66}^{2} n^{3},

a_{6} = - C_{45} C_{66}^{2} n^{3} - C_{44} C_{66}^{2} n^{4} - C_{12} C_{22} C_{44} n^{4} - C_{12} C_{22} C_{45} n^{3} - C_{22} C_{44} C_{66} n^{2}

+ C_{22} C_{44} C_{66} n^{4} - C_{22} C_{44} C_{66} n^{6} + C_{22} C_{45} C_{66} n^{3} - C_{22} C_{45} C_{66} n^{5} - C_{22} C_{45} C_{66} n .

The relationship between zero and first components of displacement field including $u_{0}$ , $v_{0}$ , $w_{0}$ , $u_{1}$ , $v_{1}$ , $w_{1}$ are also as follows:

12a

(C_{11} (λ + 1)^{2} u_{1}) - C_{22} u_{1} - 2 C_{12} n v_{1} - C_{12} n λ v_{1} - C_{66} n λ v_{1} + C_{22} n v_{1} - C_{45} n z w_{0}

- C_{55} ζ λ w_{0} = 0,

12b

C_{66} n λ u_{0} + 3 C_{66} n u_{1} + C_{66} n λ u_{1} + C_{12} (λ + 1) (n + 1) u_{1} + C_{12} λ u_{0} + C_{22} n u_{1} + C_{22} u_{0}

- C_{66} λ^{2} v_{1} - C_{22} n^{2} v_{1} - C_{22} n v_{0} - C_{44} n ζ w_{0} - C_{45} ζ λ w_{0} = 0,

12c

C_{55} ζ λ u_{0} + C_{55} ζ u_{0} - C_{45} n ζ u_{0} - C_{45} ζ λ v_{0} - C_{45} ζ v_{0} - C_{44} n ζ v_{0} - 3 C_{45} n w_{1} - 2 C_{45} n λ w_{1}

+ C_{55} (λ + 1)^{2} w_{1} - C_{44} n^{2} w_{1} = 0 .

Finally the recurrence equations are written as:

13a

[C_{11} (k + λ)^{2} - C_{66} n^{2} - C_{22}] u_{k} + [ρ ω^{2} - C_{55} ζ^{2}] u_{k - 2} + [- C_{12} n (k + λ) + C_{66} n

{- C}_{66} n (k + λ)] v_{k} - C_{45} ζ^{2} v_{k - 2} + [- ζ (C_{45} n + C_{55} (k + λ)] w_{k - 1} = 0,

13b

[C_{66} n (k + λ) + C_{12} n (k + λ) + C_{22} n + 2 C_{66} n] u_{k} + [C_{12} (k + λ) + C_{12}] u_{k - 1}

{- C}_{45} ζ^{2}] u_{k - 2} + [- C_{66} + C_{66} (k + λ)] v_{k} + [C_{22} [n - C_{44} n ζ - C_{45} ζ (k + λ)] v_{k - 1}

+ ρ ω^{2} v_{k - 2} = 0,

13c

[C_{55} ζ (k + λ) - C_{45} n ζ + C_{55} ζ] u_{k - 1} + [- C_{45} ζ (k + λ) - C_{44} n ζ - C_{45} ζ] v_{k - 1}

+ [- 2 C_{45} n (k + λ) + C_{55} (k + λ) (k + λ - 1) - C_{44} n^{2} - C_{45} n + C_{55} (k + λ)] w_{k}

+ [- C_{33} ζ^{2} - C_{33} ζ + ρ ω^{2}] w_{k - 2} = 0 .

3. Eigenvalues extraction of FGM cylindrical shells

To determine the natural frequency of the system, the Rayleigh-Ritz method is used. The energy functional $η$ defined by Lagrangian function which is written as follows:

14

η = T_{m a x} - U_{m a x},

where $T_{m a x}$ and $U_{m a x}$ are the maximum kinetic energy and strain energy of a cylindrical shell respectively and are defined as follows:

15

U_{m a x} = \frac{1}{2} \int_{0}^{L} \int_{0}^{2 π} [σ_{z} {(- \frac{\partial w}{\partial z})}^{2} + σ_{θ} {(\frac{1}{r} (u_{θ} - \frac{\partial w}{\partial θ}))}^{2}

{+ (σ}_{z} + σ_{θ}) {(\frac{1}{2} (- \frac{1}{r} \frac{\partial u_{r}}{\partial θ} + \frac{\partial u_{θ}}{\partial z}))}^{2}] r d θ d z,

16

T_{m a x} = \frac{1}{2} \int_{0}^{L} \int_{0}^{2 π} ρ h [{(\frac{\partial u_{r}}{\partial t})}^{2} + {(\frac{\partial u_{θ}}{\partial t})}^{2} + {(\frac{\partial w}{\partial t})}^{2}] r d θ d z .

Now, the lagrangian function $η$ should be minimized with respect to unknown coefficients of the cylindrical shell $u_{0}$ , $v_{0}$ and $w_{0}$ as follows:

17

\frac{\partial η}{\partial u_{0}} = \frac{\partial η}{\partial v_{0}} = \frac{\partial η}{\partial w_{0}} .

Performing the minimization as in Eq. (17) yields a set of equations that can be expressed in matrix form as follows:

18

[\begin{array}{l} Q_{11} & Q_{12} & Q_{13} \\ Q_{12} & Q_{22} & Q_{23} \\ Q_{13} & Q_{23} & Q_{33} \end{array}] \{\begin{array}{l} u_{0} \\ v_{0} \\ w_{0} \end{array}\} = \{\begin{array}{l} 0 \\ 0 \\ 0 \end{array}\},

where in Eq. (18) $Q_{i j}$ are some coefficients defined as follows:

Q_{11} = (ρ h r r^{2 λ} ω^{2}) (π L + \frac{1}{8 n ζ}) + (\frac{p_{z}}{8 π} - \frac{p_{m} r^{2}}{8}) (\frac{2}{r^{2}} n^{2} r^{2 λ} (π L + \frac{1}{8 n ζ}))

+ (- \frac{p_{z}}{8 π} + \frac{p_{m} r^{2}}{8}) (\frac{1}{4 ζ r^{2}} n r^{2 λ}) Q_{12} = (\frac{p_{z}}{8 π} - \frac{p_{m} r^{2}}{8}) (- \frac{1}{8 n ζ} \frac{2}{r} n ζ r^{2 λ})

+ (- \frac{p_{z}}{8 π} + \frac{p_{m} r^{2}}{8}) (\frac{1}{4 r} r^{2 λ}),

Q_{13} = 0,

\begin{array}{l} Q_{22} = (ρ h r r^{2 λ} ω^{2}) (π L - \frac{1}{8 n ζ}) - p_{m} r^{2 λ} (π L + \frac{1}{8 n ζ}) \end{array}

+ (\frac{p_{z}}{8 π} - \frac{p_{m} r^{2}}{8}) (4 ζ^{2} r^{2 λ} (π L + \frac{1}{8 n ζ}) + \frac{1}{8 n ζ} p_{m} r^{2 λ}) + (- \frac{p_{z}}{8 π} + \frac{p_{m} r^{2}}{8}) (\frac{1}{2 n} ζ r^{2 λ}),

Q_{23} = p_{m} n r^{2 λ} (\frac{1}{8 n ζ}) + (\frac{p_{z}}{8 π} - \frac{p_{m} r^{2}}{8}) (\frac{p_{m}}{8 ζ} r^{2 λ}),

\begin{matrix} Q_{33} = ρ h r r^{2 λ} ω^{2} [π L - \frac{1}{8 n ζ}] + \frac{p_{z}}{2 π} ζ^{2} r^{2 λ} (π L + \frac{1}{8 n ζ}) - p_{m} n^{2} r^{2 λ} (π L + \frac{1}{8 n ζ}) \end{matrix}

+ (\frac{p_{z}}{8 π} - \frac{p_{m} r^{2}}{8}) (\frac{p_{z}}{2 π} ζ^{2} r^{2 λ} (\frac{1}{8 n ζ}) - \frac{p_{m}}{8 ζ} n r^{2 λ}) .

Eq. (18) is solved by imposing the condition of non-trivial solutions and equating the characteristic determinant $[Q_{i j}]$ to zero. In order to obtain natural frequency of system, the amount of $λ$ should be obtained. For this purpose, solving the Eq. (11) will result in six $λ$ which the positive and smallest one is desired for obtaining the natural frequency of system. For the specification presented in this paper these calculated $λ$ are obtained as follows:

λ = \pm 3738.4, \pm 17.1, \pm 0.6 .

Therefore, the smallest and positive one, i.e. 0.6, is substituted into the Eq. (18) to calculate the coefficients of the Eq. (19). Expanding the characteristic determinant will result in a polynominal defined as follows:

19

α_{0} ω^{6} + α_{1} ω^{4} + α_{2} ω^{2} + α_{3} = 0,

where $α_{i}$ ; $i =$ 0, 1, 2, 3 are some constants. The roots of Eq. (19) can be obtained using the MATLAB software. Solving the Eq. (19) yields six natural frequencies that the smallest of these six natural frequencies is of interest to the presented study. In adittion, Fig. 1 shows the algorithm applied for calculating the natural frequency of the system.

4. Numerical results

In this paper, studies are presented on vibration of a simply supported functionally graded cylindrical shell as depicted in Fig. 2.

The functionally graded material (FGM) considered is composed of copper and tungsten and their properties are graded in the thickness direction according to power law distribution. The effects of the FGM configuration are studied by studying the frequencies of two FG cylindrical shells as follows:

• Type I: FG cylindrical shell has copper on its outer surface and its property vary in the thickness direction.

• Type II: FG cylindrical shell has tungsten on its outer surface and its property vary in the thickness direction.

Fig. 1The algorithm of calculating the natural frequency of the system

Fig. 2Geometry of a cylindrical shell

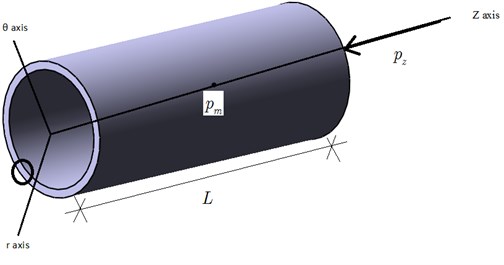
The material properties for both copper and tungsten are presented in Table 1.

Also, Table 2 shows general geometry data for cylindrical shell composed of both copper and tungsten materials.

Table 1General properties of material

Material I (copper)		Material II (tungsten)
$E_{c u}$	115 Gpa	$E_{w}$	400 GPa
$ρ_{c u}$	8.96 gr/cm³	$ρ_{w}$	15.63 gr/cm³
$υ_{c u}$	0.31	$υ_{w}$	0.28

Table 2General geometry data for cylindrical shell

Characteristics	Value	Unit
$h$	20	mm
$L$	200	mm
$r$	50	mm

The natural frequencies of the shell are discussed here. Table 3 shows variation of natural frequency versus circumferential wave number for copper FG material for different internal and external pressure. It is obvious that internal pressure increases the natural frequency of the system while external pressure decrease the natural frequency of the system.

The variation of the first lowest frequency as a function of circunferential wave number ( $n$ ) for FG cylinderical shell composed of copper and tungsten with $h / L =$ 0.02 and 0.2 and also $p_{m} = p_{z} =$ 50 Pa are shown in Fig. 3. It is noted that the frequencies in both copper and tungsten FG cylinderical shells increases as the wave number is increased. It is also easily seen from Fig. 3 that the frequency values in both copper and tungsten FG cylindrical shells increase as the $h / L$ ratio decrease. Moreovere, at the same $h / L$ ratio, the frequency value in copper FG cylindrical shell is higher than tungsten FG cylindrical shell.

Fig. 4 shows the effects of increasing axial compression force at constant internal pressure ( $p_{m} =$ 900×10³ Pa) on behavior of the natural frequency of the system for different $h / L$ ratios. According to this figure, the natural frequency of the system is enhanced as the $h / L$ ratio increases. Also, with increasing the axial compression force, the system tends to show an instability behavior which leads into buckling of the FG cylindrical shell. The critical axial compression force can be predicted where the natural frequencies curve intersect the abscissa while it can be estimated as $p_{c r} =$ 7065 N.

Table 3Variation of natural frequency (Hz) against circumferential wave number n for different internal pressure and external pressure made by copper

Natural frequency of FG cylindrical shell made by copper (Hz)
Internal pressures			External pressure
$n$	$p_{m} =$ 10⁵ (Pa)	$p_{m} =$ 10³ (Pa)	$p_{m} =$ –200 (Pa)
2	18.74	18.24	14.43
3	28.18	21.86	14.47
4	37.62	26.07	14.55
5	47.06	30.57	14.66
6	56.51	35.30	14.76
7	65.95	40.15	14.87
8	75.39	45.09	14.96
9	84.83	50.11	15.05
10	94.27	55.17	15.13

Fig. 3Effect of circumferential wave number (n) on the lowest frequency for copper and tungsten FG cylindrical shells for pm=pz= 50 Pa

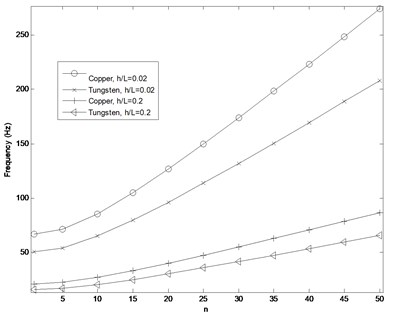
Fig. 4Variation of natural frequency VS axial compression force (N) at different h/L ratios for copper FG cylindrical shell under internal pressure pm= 900×103 Pa

Variation of natural frequency VS axial compression force (N) at different h/L ratios for copper FG cylindrical shell under internal pressure pm= 900×103 Pa

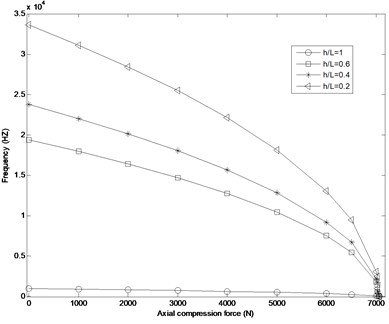
Fig. 5 shows the variation of natural frequency versus axial compression force ( $N$ ) for different $h / L$ ratios. But, the internal pressure at this case is $p_{m} =$ 50×10³ Pa. Comparing the results presented in Figs. 4 and 5, indicate that with decreasing the internal pressure, the natural frequencies of the shell are significantly decreased. The results also reveal that the critical buckling of the shell will be happened more rapidly as the internal pressure of the shell is decreased.

Table 4 shows variation of natural frequency against circumferential wave number made of tungsten FG material for different internal and external pressure. It is obvious that increasing the internal pressure leads to increasing the natural frequency of the system while increasing the external pressure behaves in opposite way.

In Fig. 6 the FG cylindrical shell that is composed of tungsten allays. It is clear that in the absence of axial compression, the natural frequency of the system composed of copper FG material (Fig. 4) at different $h / L$ ratios are greater than that of composed from tungsten FG material at the same internal pressure ( $p_{m} =$ 50×10³ Pa). Furthermore, the corresponding critical buckling load for copper FG material is a bit greater than tungsten FG cylindrical shell.

Fig. 5Variation of natural frequency VS axial compression force (N) at different h/L ratios for copper FG cylindrical shell and pm= 50×103 Pa

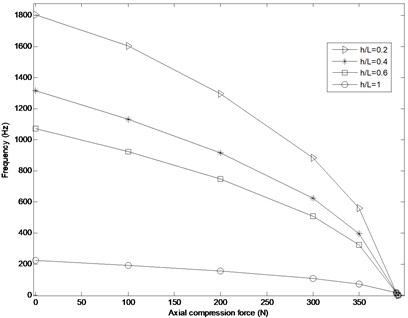
Fig. 6Variation of natural frequency VS axial compression force (N) at different h/L ratios for tungsten FG cylindrical shell and pm= 900×103 Pa

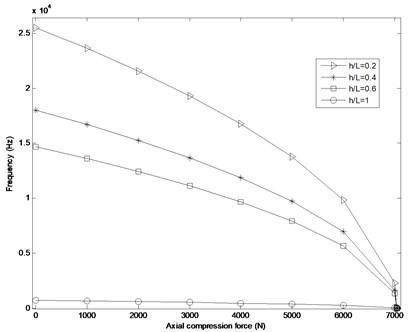
Table 4Variation of natural frequency (Hz) against circumferential wave number n for different internal pressure and external pressure made by tungsten

	Natural frequency of FG cylindrical shell made by tungsten (Hz)
Internal pressures			External pressure
$n$	$p_{m} =$ 10⁵ (Pa)	$p_{m} =$ 10³ (Pa)	$p_{m} =$ –200 (Pa)
2	47.7	13.81	10.93
3	71.8	16.55	10.95
4	95.8	19.71	11.02
5	119.9	23.15	11.10
6	143.9	26.72	11.18
7	167.9	30.40	11.26
8	192	34.14	11.33
9	216	37.94	11.40
10	240.1	41.77	11.46

Comparing Figs. 5 and 7 reveals that the buckling load in system composed of copper FG material is a bit greater than that those of composed of tungsten FG material at the same internal pressure. It means that both of these systems have the same durability under the similar axial load. However, the system made from tungsten is more expensive than copper one.

In order to verify the results, a comparison has been done between the presented work and the work done by Vodentitcharova [17] for an isotropic shell without axial load. The results are listed in Table 5. Comparing the results indicate the good agreement specially in lower $L / r$ . The Flugge theory, which is essentially a non-symmetric classical theory, was used in the work done by Vodentitcharova [17]. This as, according to Leissa [18], the Flugge theory, differs from the other classical theories, specially for $n \geq 2$ in lower frequencies. Therefore, as listed in Table 5, as the $L / r$ ratio increases, or $r / h$ ratio decreases, the difference between the two sets of results increases.

Fig. 7Variation of natural frequency VS axial compression force (N) at different h/L ratios for tungsten FG cylindrical shell and pm= 50×103 Pa

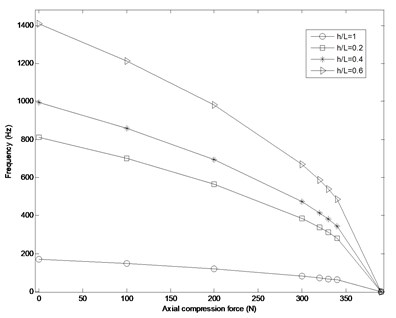
Table 5Buckling pressure and mode number for simply-simply supported end

$L / r$	$r / h$	$n$	$P_{c r}$ (Pa)	$P_{c r}$ (Pa) Ref. [17]
0.5	300	17	249438.82	332430
	3000	33	841.15	1083.1
1	300	13	190683.77	168520
	500	15	48063.78	47412
	1000	18	8710.41	8468.1
	1500	20	5127.71	3089.7
	2000	22	1006.96	1512
	3000	24	453.59	550.4
2	300	10	101146.62	86917
	3000	17	231.18	277.9
3	300	8	87902.27	57674
	3000	14	175.87	185.6
5	300	6	35557.94	34769
	3000	11	98.15	111.3

5. Conclusion remarks

In this paper, vibration of two types of functionally graded (FG) cylindrical shells under combined uniform internal pressure and axial compression load was investigated. The governing equation of the system was extracted using an exact three dimensional elasticity theory. Then, the analysis was carried out with Frobenius power series method. Also, the Rayleigh-Ritz method was used to predict the natural frequency of the system. The critical bucking loads for copper and tungsten FG cylindrical shells were computed. A comparison of the analysis was carried out by comparing the presented results with those in the literature which shows good agreement with other analytical data. The results will be differed as the $L / r$ ratio increases, or the $r / h$ ratio decreases. It is due to the fact that the presented work used 3D wave propagation which completely considers all the wave components. Furthuremore, under identical internal pressure for both copper and tungsten FG cylindrical shells, the copper FG cylindrical shell is a bit stronger than the tungsten FG cylindrical shell. Although, for different $h / L$ ratios, the frequency values in copper FG cylindrical shell are more than tungsten FG cylindrical shell.

References

Shao Z. S., Wang T. J. Three-dimensional solutions for the stress fields in functionally graded cylindrical panel with finite length and subjected to thermal/mechanical loads. International Journal of Solids and Structures, Vol. 43, Issue 13, 2006, p. 3856-3874.

Search CrossRef
Malekzadeh P., Ghaedsharaf M. Three-dimensional free vibration of laminated cylindrical panels with functionally graded layers. Composite Structures, Vol. 108, 2014, p. 894-904.

Search CrossRef
Daneshjou K., Shokrieh M. M., Ghorbani Moghaddam M., Talebitooti R. Analytical model of sound transmission through relatively thick FGM cylindrical shells considering third order shear deformation theory. Composite Structures, Vol. 93, 2010, p. 67-78.

Search CrossRef
Sheng G. G., Wang X. An analytical study of the non-linear vibrations of functionally graded cylindrical shells subjected to thermal and axial loads. Composite Structures, Vol. 97, 2013, p. 261-268.

Search CrossRef
Jin Guoyong, Xie Xiang, Liu Zhigang The Haar wavelet method for free vibration analysis of functionally graded cylindrical shells based on the shear deformation theory. Composite Structures, Vol. 108, 2014, p. 435-448.

Search CrossRef
Ebrahimi M. J., Najafizadeh M. M. Free vibration analysis of two-dimensional functionally graded cylindrical shells. Applied Mathematical Modelling, Vol. 38, Issue 1, 2014, p. 308-324.

Search CrossRef
Asgari M., Akhlaghi M. Natural frequency analysis of 2D-FGM thick hollow cylinder based on three-dimensional elasticity equations. European Journal of Mechanics A/Solids, Vol. 30, Issue 2, 2011, p. 72-81.

Search CrossRef
Shakeri M., Akhlaghi M., Hoseini S. M. Vibration and radial wave propagation velocity in functionally graded thick hollow cylinder. Composite Structures, Vol. 76, Issues 1-2, 2006, p. 174-181.

Search CrossRef
Hasheminejad Seyyed M., Ahamdi-Savadkoohi Ali Vibro-acoustic behavior of a hollow FGM cylinder excited by on-surface mechanical drives. Composite Structures, Vol. 92, Issue 1, 2010, p. 86-96.

Search CrossRef
Seyed Mahmoud Hosseini Analysis of elastic wave propagation in a functionally graded thick hollow cylinder using a hybrid mesh-free method. Engineering Analysis with Boundary Elements, Vol. 36, Issue 11, 2012, p. 1536-1545.

Search CrossRef
Taj M. N. A. G., Chakrabarti A. Dynamic response of functionally graded skew shell panel, Latin American. Journal of Solids and Structures, Vol. 10, Issue 6, 2013, p. 1243-1266.

Search CrossRef
Pradhan K. K., Chakraverty S. Free vibration of Euler and Timoshenko functionally graded beams by Rayleigh-Ritz method. Composites: Part B, Vol. 51, 2013, p. 175-184.

Search CrossRef
Sun S., Cao D., Han Q. Vibration studies of rotating cylindrical shells with arbitrary edges using characteristic orthogonal polynomials in the Rayleigh-Ritz method. International Journal of Mechanical Sciences, Vol. 68, 2013, p. 180-189.

Search CrossRef
Biglar M., Mirdamadi H. R., Danesh M. Optimal locations and orientations of piezoelectric transducers on cylindrical shell based on gramians of contributed and undesired Rayleigh-Ritz modes using genetic algorithm. Journal of Sound and Vibration, Vol. 333, Issue 5, 2014, p. 1224-1244.

Search CrossRef
Jin G., Su Z., Shi S., Ye T., Gao S. Three-dimensional exact solution for the free vibration of arbitrarily thick functionally graded rectangular plates with general boundary conditions. Composite Structures, Vol. 108, 2014, p. 565-577.

Search CrossRef
Toorani M. H., Lakis A. A. General equation of anisotropic plates and shells including transverse shear deformation, rotary inertia and initial curvature effects. Journal of Sound and Vibration, Vol. 237, Issue 4, 2000, p. 561-615.

Search CrossRef
Vodenitcharova T., Ansourian P. Buckling of circular cylindrical shells subject to uniform lateral pressure. Engineering Structures, Vol. 18, Issue 8, 1996, p. 604-614.

Search CrossRef
Leissa W. Vibration of Shells. National Aeronautics and Space Administration, Washington D.C., 1973.

Search CrossRef

About this article

Received

06 August 2014

Accepted

20 December 2014

Published

15 May 2015

SUBJECTS

Modal analysis

Keywords

functionally graded material (FGM)

Frobenius power series method

Rayleigh-Ritz method

eigenvalue

Acknowledgements

This paper is extracted from the Research Project called “Three Dimensional Wave Propagation in FG Cylindrical Shells“ which is supported by Islamic Azad University, Central Tehran Branch in Iran. The authors would like to express their gratitude to that research centre for their support and also the referees for many valuable comments which improve the presentation of this paper.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.