Fractional order generalized thermoelasticity with variable thermal conductivity

1. Introduction

Biot introduced the first coupled theory of thermoelasticity in which the equations of heat conduction and elasticity became coupled and agree with physical behavior of the elastic materials, where any change of the temperature gives a certain amount of strain in an elastic body and vice versa [1]. The equations of this theory consist of the equation of motion, which is a hyperbolic partial differential equation, and the heat equation, which is parabolic and implies that if an elastic medium is extending to infinity subjected to a thermal or mechanical disturbance, the effect will vanish instantaneously at infinity, which contradicts physical experiments. Hence, a new equation of energy with hyperbolic type is needed.

Lord and Shulman constructed the theory of generalized thermoelasticity with one relaxation time for the particular case of an isotropic body [2]. Dhaliwal and Sherief extended this theory to include the anisotropic case [3]. According to this theory, a modified law of heat conduction including both the heat flux and its time rate of change, which is called Cattaneo’s heat conduction, replaces the conventional Fourier’s law. Now, the heat equation is hyperbolic and hence it introduces finite speeds of propagation for mechanical and thermal waves.

The physical property of a solid body related to application of heat energy is defined as a thermal property. Thermal properties explain the response of a material to the application of heat and one of the most important thermal properties is the thermal conductivity. Thermal conductivity $K$ is ability of a material to transport heat energy through it from high temperature region to low temperature region and it is a microstructure sensitive property its value range for metals 20-400, for ceramics 2-50 and for polymers order of 0.3. Heat is transported in two ways – electronic contribution, vibrational (phonon) contribution. In metals, electronic contribution is very high. Thus metals have higher thermal conductivities. Thermal conductivity of iron initially decreases then increases slightly; thermal conductivity decreases with increase in temperature for aluminium; while it increases for platinum and gold [4]. Godfrey has reported decreases of up to 45 % in the thermal conductivity of various samples of silicon nitride between (1 and 400.0 C). The question arises: what are the effects of these variations on the stress and displacement distributions in metal components [5]?

Youssef used the state-space approach to solve a problem of generalized thermoelasticity for an infinite material with a spherical cavity and variable thermal conductivity subjected to ramp-type heating [6].

Recently, the fractional calculus has been used to modify many existing models of physical processes. Abel is the first one who gives an application of fractional derivatives by applied fractional calculus in the solution of an integral equation. The connection between fractional derivatives and the theory of linear viscoelasticity has been found by Caputo [7]. The theory of fractional calculus introduced mathematical modeling to simulate the polymers materials successfully.

A new formula of heat conduction has been considered in the context of the fractional integral operator definition by Youssef [8]. This new consideration generated the fractional order generalized thermoelasticity which was cited by Youssef who approved the uniqueness of its solutions [9].

Youssef solved one dimensional problem in the context of the fractional order generalized thermoelasticity and discussed the effects of the fractional order parameter on all the studied fields in [8] and with Al-Leheabi in [9]. Youssef and Al-Leheabi get the variational principal of the theorem [10]. Kumar et al. discussed the plane deformation due to thermal source in fractional order thermoelastic media [11], while Abo-Dahab and Abbas solved a problem of LS model on thermal shock problem of generalized magneto-thermoelasticity for an infinitely long annular cylinder with variable thermal conductivity [12]. Abbas and Abo-Dahab got the numerical solution of thermal shock problem for generalized magneto-thermoelasticity for an infinitely long annular cylinder with variable thermal conductivity [13].

The counterparts of our problem in the contexts of the thermoelasticity theories have been considered by Sharma and Marin [14] and Marin et al. [15, 16].

In the present work, the solution of thermoelastic medium thermal loaded by thermal shock is developed in the context of fractional order generalized thermoelasticity with variable thermal conductivity. Laplace transform methods are used to determine the temperature, the displacement, the strain and the stress. The effect of the variability of thermal conductivity has been studied together with the fractional order parameter and represented graphically with some comparisons.

2. Basic formulations

In the context of the fractional order generalized thermoelasticity, the displacement and the thermal fields as well as the stress-strain-temperature relations for a linear homogeneous and isotropic medium are in the forms [8, 9].

The equations of motion take the form:

where $\lambda \text{,}$$\mu$ are Lame’s constants, $u_i$ is the displacement component, $F_i$ is the body force component, $\gamma ={\alpha }_T\left(3\lambda +2\mu \right)$ and ${\alpha }_T$ is the thermal expansion, $T$ is the temperature of the body, $T_o$ is the reference temperature, $\theta =\left(T-T_o\right)$ is the increment of the temperature, $\rho$ is the density, the subscript $i$ and $j$ give the order of the component tensor of a function in three dimensions and $u_{i,j}=\partial u_i/\partial \mathrm{}{x}_j$ which means the derivative of the component of the displacement $u_i$ with respect to the $x_i$-axis.

The heat equations take the form [7]:

where ${\tau }_o$ is the relaxation time, $K$ is the thermal conductivity, $\kappa$ is called the thermal diffusivity, and the fractional integral operator defined as follows [8, 9]:

where $\mathrm{\Gamma }\left(\alpha \right)$ is the Gamma function.

The constitutive equations take the form:

where ${\sigma }_{ij}$ is the stress tensor and ${\delta }_{ij}$ is the Kronecker delta function.

The strain-displacement equations take the form:

For one-dimensional half-space $0\le x<\mathrm{\infty }$ of an elastic medium as in Fig. 1 without any body forces with variable thermal conductivity and displacement components $u_i=\left(u\left(x,t\right),\mathrm{0,0}\right)$, the equations in (1), (2), (4) and (5) take the forms:

Fig. 1One-dimensional half-space of an elastic medium

We will consider the thermal conductivity has the following linear form of thermo-dynamical temperature as follows [6]:

where $K_o$ is constant and gives the thermal conductivity of the material when it does not depend on $\theta$, and $K_1$ small constant parameter.

Now, we will use the following mappings [6]:

Differentiating Eq. (6) with respect to $x$ yields:

Differentiating again the above equation with respect to $x$ we obtain:

Differentiating Eq. (11) with respect to the time $t$, we get:

Substituting from Eqs. (13) and (14) in Eq. (7), we obtain:

From Eqs. (10) and (12) we have:

Thus Eq. (6) will take the form:

From Eqs. (10) and (12), we obtain:

Hence, we have:

Now, if we consider that $D^{\alpha -1}$ is the fractional derivative as an inverse operator of the integral operator $I^{\alpha -1}$, then we can write Eq. (12) in the form:

where $D^{\alpha }={\partial }^{\alpha }/\partial \mathrm{}{t}^{\alpha }$.

For simplicity we use the following non-dimensional variables:

Now, we have the following system of coupled equations:

where $a=\gamma \mathrm{}{T}_o/\mu \mathrm{}{\beta }^2$ and $g=\gamma \mathrm{}\mathrm{}\kappa /K_o$.

To solve the above system we have to determine a certain boundary conditions, so we will consider the bounding plane of the half-space ($x=$ 0) is thermally shocked and has a rigid foundation, so we have:

where $H\left(t\right)$ is the Heaviside unite step function which gives after using Eq. (18) that:

3. Governing equations in the Laplace transform domain

Applying the Laplace transforms for Eqs. (21)-(24) define by the formula:

Hence, we obtain the following system of differential equations:

Eqs. (25) and (26) can be written in a vector-matrix differential equation as follows [20]:

where:

where:

4. Solution of the vector-matrix differential equation

Let us now proceed to solve Eq. (29) by the eigenvalue approach proposed by [17]. The characteristic equation of the matrix $A$ takes the form:

The roots of the characteristic Eq. (15) which are also the eigenvalues of matrix $A$ are of the form $\lambda =\pm {\lambda }_1$, $\lambda =\pm {\lambda }_2$.

The eigenvector $\overrightarrow{X}={\left[x_1,x_2,x_3,x_4\right]}^T$, corresponding to eigenvalue $\lambda$ can be calculated as:

From Eqs. (33), we can easily calculate the eigenvector ${\overrightarrow{X}}_j$, corresponding to eigenvalue ${\lambda }_j$, $j=\mathrm{}$1, 2, 3, 4.

For further reference, we shall use the following notations:

The solution of Eq. (26) can be written from as follows:

where the terms containing exponentials of growing nature in the space variable $x$ have been discarded due to the regularity condition of the solution at infinity, $B_1$ and $B_2$ are constants to be determined from the boundary condition of the problem. Thus, the field variables can be written for $x$ and $s$ as:

To complete the solution we have to know the constants $B_1$ and $B_2$, by using the boundary conditions Eqs. (27) and (28) we obtain:

where $R_{11}=x_3^1$, $R_{12}=x_3^2$, $R_{21}=x_4^1$, $R_{22}=x_4^2$.

5. Numerical inversion of the Laplace transform

In order to determine the conductive and thermal temperature, displacement and stress distributions in the time domain, the Riemann-sum approximation method is used to obtain the numerical results. In this method, any function in Laplace domain can be inverted to the time domain as:

where $\mathrm{R}\mathrm{e}$ is the real part and $i$ is imaginary number unit. For faster convergence, numerous numerical experiments have shown that the value of $\epsilon$ satisfies the relation $\epsilon t\approx \text{4.7}$ [18].

6. Numerical results and discussion

The copper material was chosen for purposes of numerical evaluations and the constants of the problem were taken as following [6]:

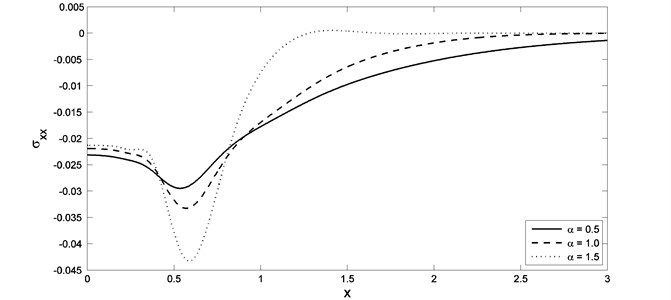
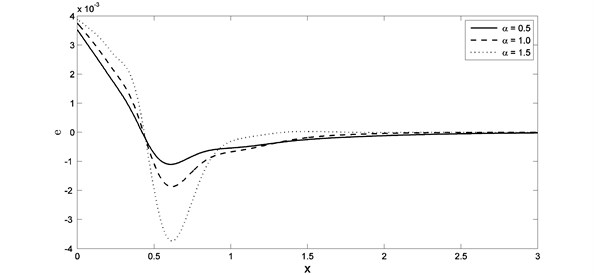
The computations were carried out for $t=\text{0.2}$ and the temperature, the stress, the displacement and the strain distributions are represented graphically for wide range of $x$$\left(\text{0}\le x\le \text{3}\right)$ and for different values of the fractional order parameter $\alpha$ ($\alpha =$ 0.5, 1.0, 1.5) when $K_1=\text{0.0}$ which gives the normal case of thermal conductivity and when $K_1=\mathrm{}$–0.5 which gives variable thermal conductivity. In Figs. 2 and 3, we found that, the parameter $\alpha$ and $K_1$ have significant effects on the temperature distributions. Fig. 2 shows that, the temperature values starting form 1.0 as the boundary condition been set, and then the waves decrease till vanish at large value of $x$ and when the value of the parameter $\alpha$ increases, the lack of temperature faster when values for distance less than. In Figs. 4 and 5, we found that, the parameter $\alpha$ and $K_1$ have significant effects on the stress distributions. When the value of the parameter $\alpha$ increases the lack of stress faster when values for distance less than. The absolute value of the maximum points of the stress increase when the value of the parameter $\alpha$ increases, while it decreases when the value of the parameter $K_1$ increases.

Fig. 2The temperature distribution with different value of fractional order parameter when K1=0.0

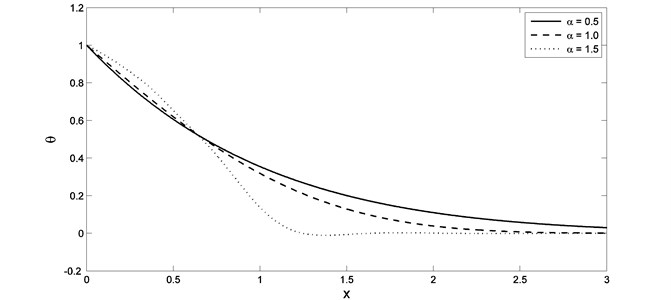
Fig. 3The temperature distribution with different value of fractional order parameter when K1= –0.5

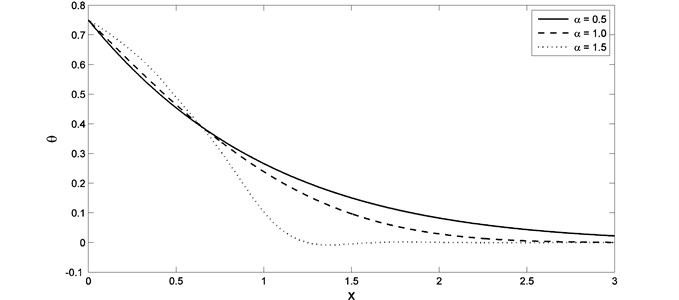
Fig. 4The stress distribution with different value of fractional order parameter when K1=0.0

In Fig. 6 and 7, we noticed that, the parameter $\alpha$ and $K_1$ have significant effects on the displacement distributions. When the value of the parameter $\alpha$ increases the lack of displacement faster when values for distance less than. The value of the maximum points of the displacement increase when the value of the parameter $\alpha$ increases, while it decreases when the value of the parameter $K_1$ increases. In Figs. 8 and 9, we noticed that, the parameter $\alpha$ and $K_1$ have significant effects on the strain distributions. When the value of the parameter $\alpha$ increases the lack of strain faster when values for distance less than. The absolute value of the maximum points of the strain increase when the value of the parameter $\alpha$ increases, while it decreases when the value of the parameter $K_1$ increases.

Fig. 5The stress distribution with different value of fractional order parameter when K1= –0.5

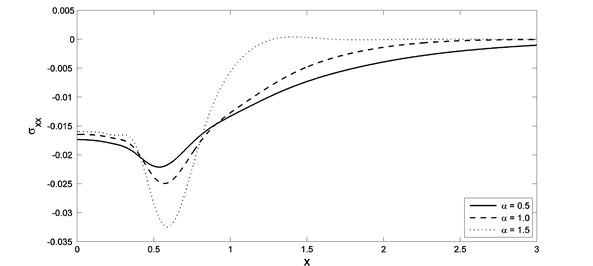
Fig. 6The displacement distribution with different value of fractional order parameter when K1=0.0

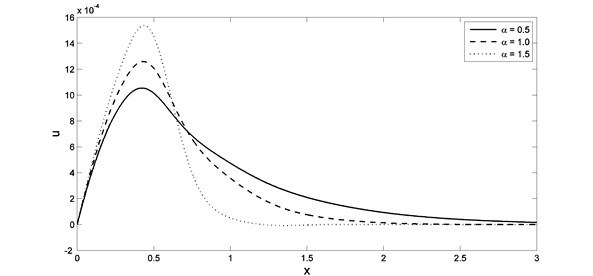
Fig. 7The displacement distribution with different value of fractional order parameter when K1= –0.5

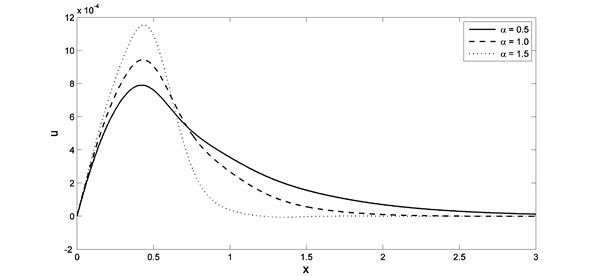
Fig. 8The strain distribution with different value of fractional order parameter when K1=0.0

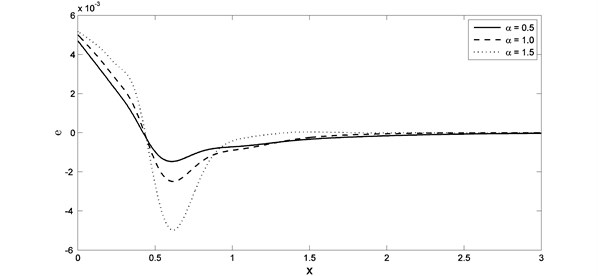
Fig. 9The strain distribution with different value of fractional order parameter when K1= –0.5

7. Conclusion

In this work, the solution of thermoelastic medium thermal loaded by thermal shock has been developed in the context of fractional order generalized thermoelasticity with variable thermal conductivity. The effect of the variability of thermal conductivity has been studied together with the fractional order parameter and represented graphically with some comparisons and we obtain that; the fractional order parameter and the variability of the thermal conductivity play a vital role on the speed of the propagation each of the thermal wave and the mechanical wave, increasing the value of the fractional order parameter makes the value of the thermal wave and the mechanical wave vanishes in shorter distance from the bounding plane, changing of the thermal conductivity causes significant changing of the values of the maximum points of the thermal wave and the mechanical wave.