Comparison of dynamic behaviors and strength among three versions of face gear drives with high contact ratios

2.1. Tooth modeling solution

A face gear tooth can be considered as a sequence in which modified involute gears are superimposed along its face width, and at the extreme outer radius, the tooth is pointing, namely positive modifications, as well as at the extreme inner radius, the tooth is undercut, mean to negative modifications. Therefore, a face gear tooth can be divided into two parts: one is a positive modification area, the other is a negative modification area. Thus, a non-modified position along face widths, that is a pitch, must be existed, and it can be expressed as:

Meanwhile, extreme inner and outer radiuses can be derived in a piecewise form as:

and modified coefficients of the extreme radiuses can be deduced in a piecewise form as:

where $\gamma$ is a shaft angle, $m$ is a module, $r_f$ and $r_b$ are dedendum and base radiuses of generative gear respectively, $\alpha$ is a pressure angle of reference circles, ${\alpha }_t^{\text{'}}$ is an addendum pressure angle, $z_g$ is the number of generative gear teeth, $z_f$ is the number of face gear teeth, $h_a^{*}$ is an addendum coefficient, $c^{*}$is a clearance coefficient and a drive ratio for generation $i_{gf}$ can be written in:

2.2. Dynamic analysis solution

In this study, a three dimensional structure of face gear drives and its four DOF lumped parameter dynamic model, which are given in Fig. 1, are established for analyzing dynamic behaviors of standard version of face gear drives and three versions of face gear drives with high contact ratios.

Fig. 1A full structure of face gear drives and its four DOF lumped parameter dynamic model

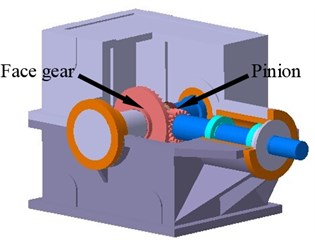
a) A three dimensional structure of face gear drives

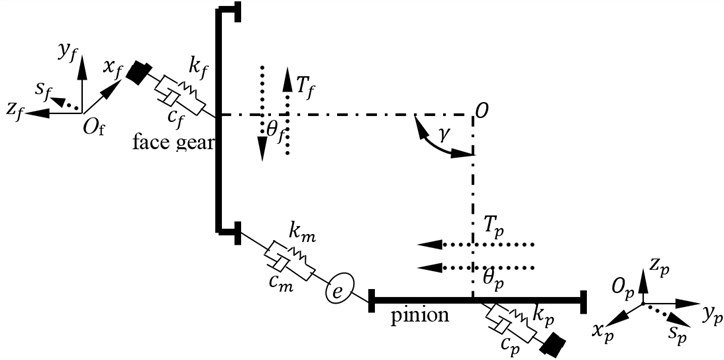
b) A four DOF dynamic model

As shown in Fig. 1, $\theta$ is a torsion degree of freedom, $s$ is a bending degree of freedom, $T$ is a torsion, $k$ is a bending stiffness, $c$ is a bending damping, subscript $f$ and $p$ express a face gear and a pinion respectively. In addition, $k_m$ is mesh stiffness, $c_m$ is mesh damping, and $e$ is a comprehensive meshing error.

Mathematic formulas of the four DOF dynamic model can be derived by:

where $m$ is a quality, $I$ is a moment of inertia, $R_b$ is a radius of base circles, $\text{'}$ is first derivative, $\text{'}\text{'}$ is second derivative, and mesh force $F_m$ can be deduced as:

2.3. Strength analysis solution

Strength analysis solution of face gear drives is constructed by ISO 6336 standard associated with an equivalent face gear tooth, which is based on the proposed tooth modeling.

Typically, the tooth number of pinion, which meshes with a face gear, is less one to three teeth than a generative gear, which is employed to generate face gears, in order to avoid offset load phenomenon. Thus, the contact position of face gear drives can not be the pitch, but on the negative modification area due to the reason of fewer teeth. A modified coefficient of the contact position can be extracted as:

where $z_p$ is the number of pinion teeth.

The spacing between the pitch and the contact position along face widths can be derived by:

where $r_{fp}$ is a pitch radius on face gears. Therefore, the contact radius on face gears can be given as:

According to Eq. (7) to Eq. (9), a contact position and its cross section on face gears are shown in Fig. 2.

Fig. 2A contact position and its cross section on face gears

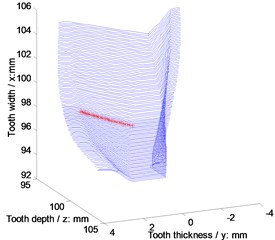
a) A contact position on face gears

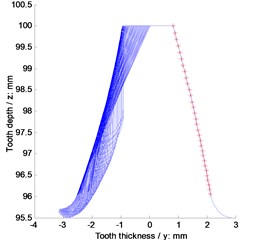
b) Contact cross section on face gears

In Fig. 2, face gear tooth profiles on contact cross sections are modified involute profiles. Thus, based on contact viewpoints, face gear drives can be equivalent to involute gear drives. An equivalent face width of face gear teeth can be considered as the minimum diameter among long axles of contact ellipses of face gear drives. According to Hertz formulas [17], an equivalent face width of face gear teeth can be deduced as:

where $F$ is a loaded force, $\gamma$ is Poisson ratio, $E$ is the elastic modulus, $r$ is a contact radius, $\mu$ and $\nu$ are elliptic integral factors.

2.4. Contact ratios of face gear drives

According to the proposed equivalent face gear drives as illustrated in Fig. 2, and the reference [18], contact ratios of face gear drives can be expressed as:

where ${\alpha }_a$ is an addendum pressure angle, ${\alpha }_{pitch}$ is a pitch pressure angle. According to the reference [18], addendum and pitch pressure angles can be written in:

where $a$ and $a\text{'}$ are theoretical and operating center distances respectively. Thus, under the same conditions of drive ratios and installation distances, high contact ratio solutions of face gear drives can be constructed by three versions, namely increasing addendum coefficients, decreasing pressure angles of reference circles, and combination with the first methods, based on Eq. (11) to Eq. (13).

3.1. Tooth geometry simulation

Geometric parameters of example cases of face gear drives are listed in Table 1. In addition, simulative face gear teeth are obtained, as shown in Fig. 3, and contact ratios of the example cases are calculated as listed in Table 2.

According to the analysis of contact ratios in Table 2, standard version is a face gear drive with a normal contact ratio, and other three versions, namely first version, second version and third version, are face gear drives with high contact ratios, which are greater than two.

Fig. 3Simulations of face gear teeth

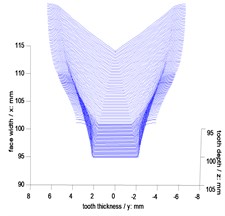
a) Standard version

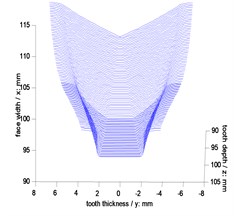
b) First version

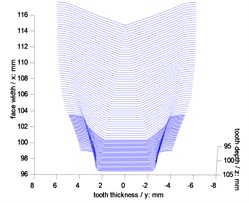
c) Second version

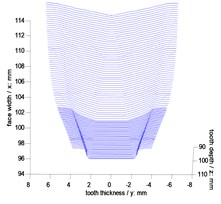
d) Third version

3.2. Dynamic behavior analysis

For the analysis of dynamic behaviors of these example cases, operating conditions and material characteristics of gears are listed in Table 3.

Fig. 4Time-varying mesh stiffness of the example cases

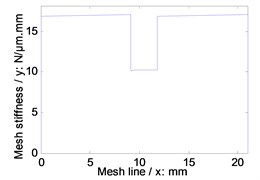
a) Standard version

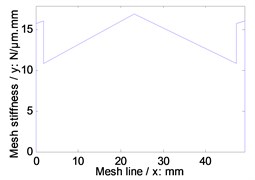
b) First version

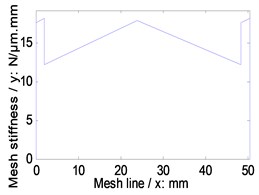
c) Second version

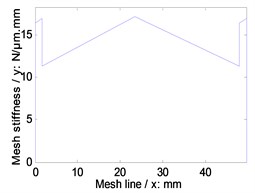
d) Third version

Simulations of time-varying and average mesh stiffness of face gear drives, which is based on the proposed tooth geometry modeling, are given in Fig. 4 and listed in Table 4, and static transmission errors under the operating conditions listed in Table 3, are calculated as shown in Fig. 5.

Fig. 5Static transmission error of the example cases

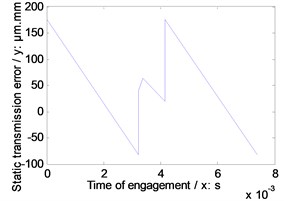
a) Standard version

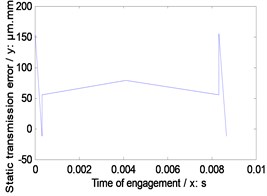
b) First version

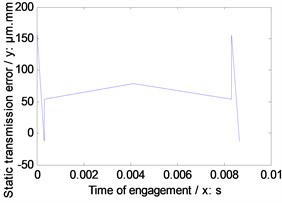
c) Second version

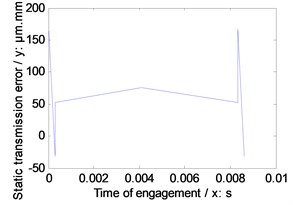
d) Third version

As illustrated in Fig. 4, Table 4 and Fig. 5, among three versions of face gear drives with high contact ratios, the best effect of decreasing average mesh stiffness is conducted by first version, and the best effect of decreasing maximum amplitude of static transmission errors is produced by second version.

Further, natural frequencies of each version are simulated in Fig. 6, gear dynamic responses and face gear dynamic mesh forces of each version are given in Fig. 7, and dynamic accelerations of bearings of each version are shown in Fig. 8.

In the case of Fig. 6 to Fig. 8, firstly, three versions of face gear drives with high contact ratios can improve vibrations of face gear drives effectively. Secondly, first version expresses a trend of increasing natural frequencies. Oppositely, second version shows that of decreasing natural frequencies, and the impact of second version on natural frequencies is greater than that by first version. Thirdly, mesh force of face gear drives would be reduced by three versions, and among three versions, the effect of second version on mesh force is best, and the impact of second version on mesh force is greater than that by first version. Furthermore, dynamic responses of bearings would be improved by three versions, specially in pinion bearings. However, the absolute difference among dynamic accelerations of bearings of three versions, which can be measured, is very small. Thus, although the effects of reducing vibrations of three versions of face gear drives with high contact ratios are excellent, which is the best among three versions is determined only by the analysis of dynamic behaviors is difficult.

Fig. 6Natural frequencies of the example cases

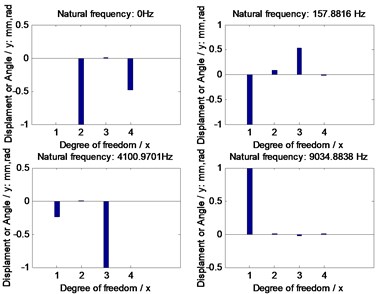
a) Standard version

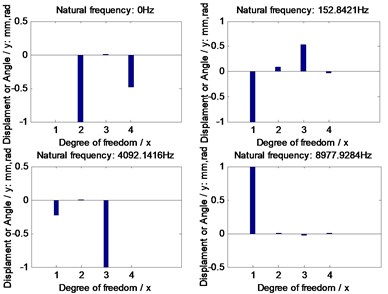
b) First version

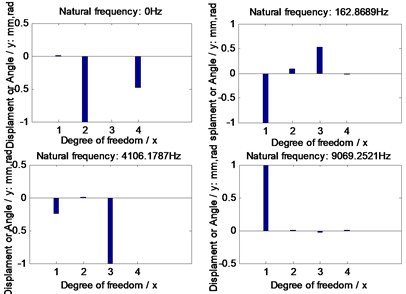
c) Second version

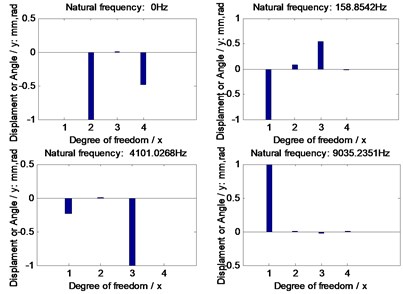
d) Third version

3.3. Strength analysis

Strength results of the example cases, which is based on ISO 6336 standard associated with the proposed equivalent face gear teeth, are calculated in Table 5.

Fig. 7Dynamic behaviors

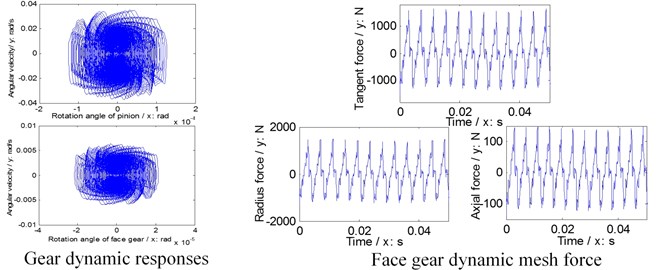
a) Standard version

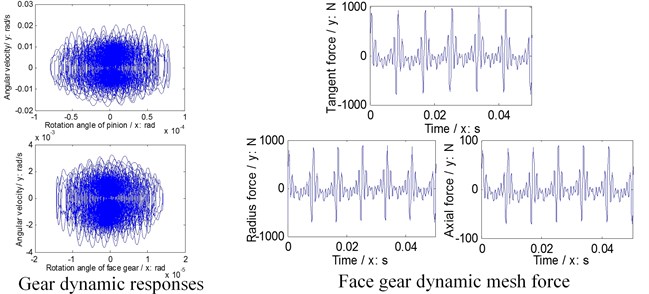
b) First version

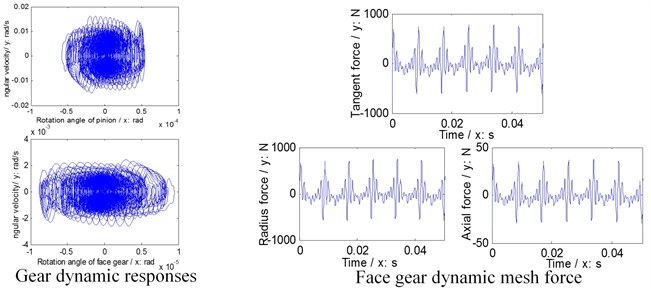
c) Second version

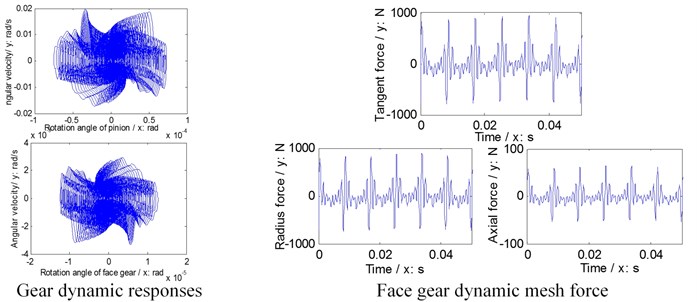
d) Third version

Fig. 8Dynamic accelerations of bearings

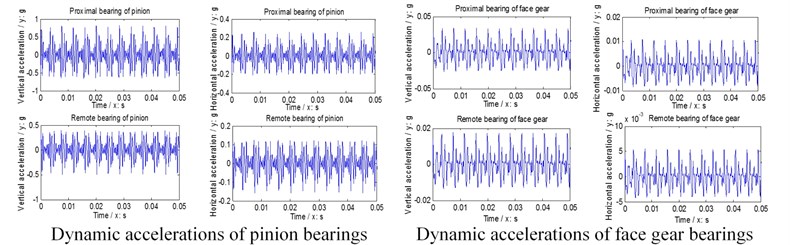
a) Standard version

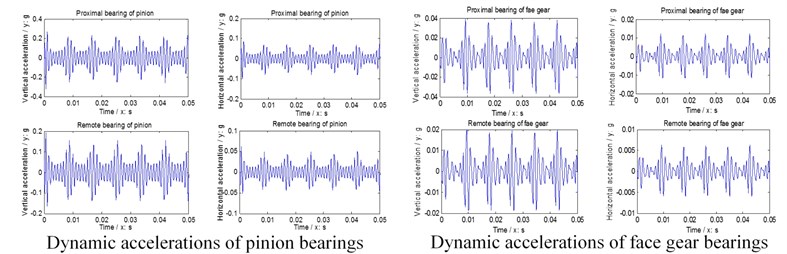
b) First version

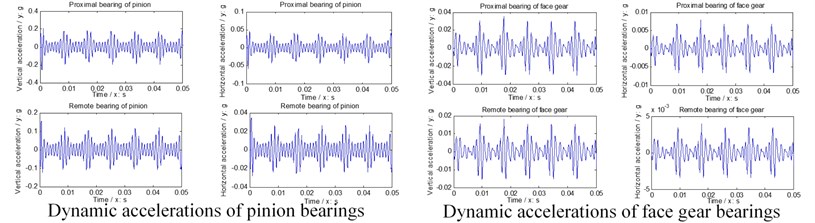
c) Second version

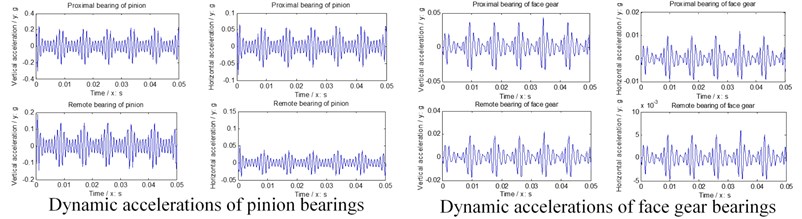
d) Third version

As illustrated in Table 5, first version would be benefit to decrease bending and contact stresses but not good for bulk temperatures. Second version would deteriorate strength of face gear drives. Third version indicates the impact of second version on strength is greater than that by first version.

According to comprehensive analysis of the dynamic behaviors and strength simulated in this issue, a result, which is three versions are effective for reducing dynamic responses of face gear drives, and the differences among three versions for dynamic behaviors of face gear drives are very small, but first version is better than other two versions for the strength of face gear drives, can be extracted. Thus, an optimization design solution of face gear drives with high contact ratios, which is the implementation of first version, namely increasing addendum coefficients of face gear drives, is recommended.