Modified cam-clay model with dynamic shear modulus under cyclic loads

Luo, Junhui; Miao, Linchang; Wang, Zhengxin; Shi, Wenbo

Journal of Vibroengineering

Browse Journal

Submit article

Published: 15 February 2015

Check for updates

Modified cam-clay model with dynamic shear modulus under cyclic loads

Junhui Luo¹

Linchang Miao²

Zhengxin Wang³

Wenbo Shi⁴

^{1, 2, 4}Institute of Geotechnical Engineering of Southeast University, Nanjing, 210096, China

³Nantong Bureau of Housing and Urban-Rural Development, Nantong, Jiangsu, 226006, China

Corresponding Author:

Linchang Miao

Cite the article Download PDF

Downloads 1632

Abstract

In order to study the dynamic characteristics of clay under metro loads, a dynamic triaxial test for clay was conducted. The function formula between the dynamic shear modulus and the number of oscillation periods was presented to calculate and analyze the dynamic characteristics of clay, then the function formula applicability was verified for different regional clays. In addition, the relationship between dynamic shear modulus and the parameters of cam-clay was established. The function formula for calculating dynamic shear modulus can be generalized to apply to the cam-clay model. The results show that the dynamic shear modulus function formula can be well applied. This modified cam-clay model can not only describe hysteresis loops, but also consider the effects of loading frequency on the dynamic characteristics of clay. Therefore, it is convenient to study the dynamic characteristics of clay under metro loads for theoretical analysis and verification.

1. Introduction

In general, the engineering characteristics of soft clays include low shear strength, high compressibility, and low permeability, but soft clay characteristics are particular to various regions [1, 2]. The Yangtze River Delta was mainly formed by erosion of sediment with a thickness of alluvium from tens of meters to 400 m from west to east. The consolidation settlement and creep deformation of the soft clay are very large in the subway under metro loads in the flood plain region of Nanjing. Under this condition, larger settlement will not only affect metro operations, but may also cause cracking of the lining structure and security problems, which induce severe mud leakage and eventually leads to secondary settlement [3]. Studying the dynamic characteristics of soft clay under cyclic loads provides evidence for the necessity of early warning and prevention of accidents in projects.

Numerous studies on the dynamic characteristics of clay have been carried out. Evaluating the dynamic characteristics of clay consists of determining the dynamic shear modulus and damping ratio. Hardin-Drnevich [4] proposed an equivalent linear visco-elastic hyperbolic model and established a dynamic shear modulus function formula on the basis of this model. Ishibashi and Zhang [5] proposed an exponential-type dynamic shear modulus-strain formula. In addition, Li [6] studied a dynamic shear modulus function formula under the fewer number of oscillation periods for low strain. Wichtmann and Triantafyllidis [7, 8] analyzed the stress history impact of dynamic characteristics within the range of small strain, and took place the normalization processing of dynamic shear modulus [9]. Additionally, they established the relationship between the dynamic shear modulus and soil physical and mechanical properties. Subramaniam [10] analyzed the relationship between the dynamic shear modulus and the plasticity index, then proposed and verified an empirical prediction formula. However, those studies mainly focused on the dynamic shear modulus function formula considering the strain. Since these studies did not consider the relationship between the dynamic shear modulus and the number of oscillation periods, they cannot be used to calculate the system settlement of the metro foundation.

The constitutive relation of soil is nonlinear [11]. Much of the existing research focuses on the dynamic shear modulus in the application of the constitutive model. Hardin [12, 13] introduced the original dynamic shear modulus empirical formula into classical elastic-plastic theory and recommended the improved maximum dynamic shear modulus of the empirical formula by considering particle shape and particle size distribution of the soil in elastic-plastic theory. Indris et al. [14] defined the ratio of initial stiffness to the corresponding arbitrary times as the dynamic softening index. Narashimha [15] introduced the dynamic softening index to the Iwan model and established a variable parameters nonlinear model considering stiffness degradation. Wang [16] proposed a combination of factors to consider for the softening index empirical formula, and introduced it to the Iwan model. These models have a few disadvantages: (1) they have excess model parameters that are difficult to be determined; (2) the constitutive models under cyclic loads do not reflect the loading frequency on soil; and (3) the models fail to describe the hysteresis loop [17, 18].

To overcome these disadvantages, a dynamic shear modulus function formula considering the number of oscillation periods has been constructed. In addition, this research proposes the concept of stable dynamic shear modulus, analyzes and validates parameters compared with other clays, and then analyzes the dynamic shear modulus softening law based on the soil mechanics theory. By analyzing the test results, an interconnection of the dynamic shear modulus and the cam-clay model are found. The function formula for calculating dynamic shear modulus can be generalized to apply to the cam-clay model. This study can provide theoretical guidance to projects with dynamic characteristics of clay under metro loads.

2. Dynamic triaxial test

2.1. Test material

The sampling site was located in the Nanjing Hexi region. Muddy clay was used as the soft clay and was more than 22 m thick. It was evenly distributed throughout the region. The characteristics of soft clay include flow plastic, local soft plastic and high natural water content. Table 1 shows the physical and mechanical properties of soft clay.

Table 1Physical and mechanical properties of soft clay

$w$ / %	$G_{s}$	$I_{p}$	$ρ$ (g/cm³)	$e_{0}$
37.3	2.72	17	1.877	0.99

2.2. Test instrument

The tests under static loads and cyclic loads were conducted by standard dynamic triaxial of the GDS companies (Geotechnical Digital Systems Instruments Ltd), as shown in Fig. 1.

Fig. 1GDS triaxial apparatus

2.3. Sample and preparation

The samples were prepared. The dynamic triaxial test operation was performed as follows:

Saturation: The samples are saturated by outdoor pumping, and mount the sample with 25 kPa confining pressure to preload, then are saturated with back-pressure of 100 kPa and confining pressure of 110 kPa.

Consolidation: Samples are performed isotropic consolidation. Depending on the overburden depth of undisturbed soil to determine the confining pressure, alternately use 75 and 150 kPa to consolidate. The dissipation of excess pore pressure is basically considered as complete primary consolidation. (This test does not consider secondary consolidation.)

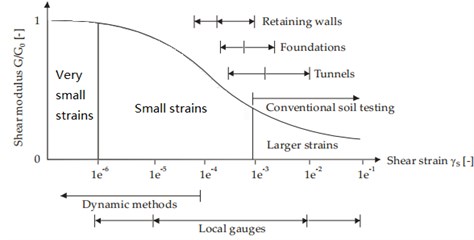
Load: In this test, half-sine wave is used to load as shown in Fig. 2. According to the results in Fig. 3 [19], different strain ranges correspond to varied types of soil projects, among which, subway tunnel foundation settlement is between 0.05 % and 1 %. The cyclic loads are set to 10, 15, and 20 N. In the case of loading, the number of oscillation periods are set to 10,000 times. When loading, some fixed measures are taken to avoid the triaxial chamber being driven by vertical bars. Fig. 1 shows the components that fix the triaxial chamber to prevent it from being driven when loading.

Fig. 2Dynamic loading mode

Fig. 3Characteristics of stiffness-strain behavior of soil with typical strain ranges for laboratory tests and structures

3. Analysis of dynamic shear modulus

3.1. Original dynamic shear modulus

The original shear modulus are calculated by the method of equivalent linear visco-elastic hyperbolic model in [4]. The data are processed based on dynamic triaxial test results. Table 2 shows the original dynamic shear modulus at different confining pressures and frequencies when the cyclic deviator loads are $F_{d} =$ 20 N.

Table 2Test values of original dynamic shear modulus

Confining pressure / kPa	Frequency / Hz	Original dynamic shear modulus Gmax / MPa
75 kPa	0.5	26.4
	1	32.5
	2	38.6
150 kPa	0.5	41.2
	1	45.4
	2	54.2

3.2. Dynamic shear modulus

Existing dynamic shear modulus functions can be divided into two categories: One type of function is dynamic shear modulus hyperbolic equations considering the strains. There are more empirical formulae of this kind, but they show no contact with time [4]. The other type of function is a dynamic shear modulus function formula considering the number of oscillation periods in [20]. This formula provides a reference for Shanghai Soft clay, but it is an empirical formula, and does not discuss the physical significance of the parameters. Additionally, it lacks application. Therefore, this paper aims to solve these problems.

3.2.1. Construction of formula

By establishing the formula, the dynamic shear modulus with the development of the number of oscillation periods of soft clay can be analyzed under the metro loads during the operation stage, so as to avoid the strain measurement. It is a simple and effective method of determining the dynamic shear modulus, and is used to facilitate the study of soil dynamics theory and rail design as well as for safety evaluation.

Fig. 4 shows the comparison of dynamic shear modulus test values and predicted values considering the number of oscillation periods. The Fig. 4 only presents one out of every ten test values. It can be observed in the figure that the test values and predicted values are well consistent. Under cyclic loads, the test values show a range of fluctuation. Eq. (1) is the calculation result:

1

G_{d} = \frac{m - k}{1 + (N / N_{0})^{p}} + k,

where $m$ is the original dynamic shear modulus; $k$ is the stable dynamic shear modulus.

Fig. 4Predicted and test values of the dynamic shear modulus

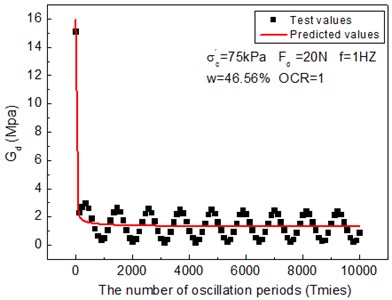
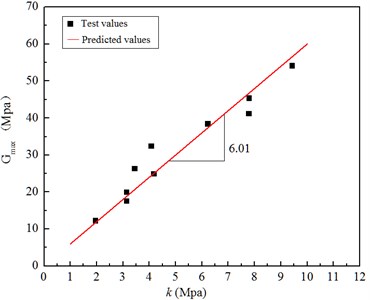
Fig. 5Relation curves between the original dynamic shear modulus and the stable dynamic shear modulus

3.2.2. Parametric analysis

In the Eq. (1):

When $N \to 0$ , $G_{d} = G_{m a x} = m$ ;

When $N \to \infty$ , $G_{d} = k$ is the stable dynamic shear modulus, namely the dynamic shear modulus of clay when the strain reaches infinity. According to [21, 22] based on the theory of critical state soil mechanics, $E_{s, O C} / E_{s, N C i} = (O C R)_{q}^{n_{0}^{*}}$ was derived. It is concluded that different soil dynamic shear modulus ratios $E_{s, O C} / E_{s, N C i}$ are used as given values in critical state. According to the critical soil mechanics, Fig. 5 shows the relationship between the original value and the stable value of the dynamic shear modulus as follows: $G_{m a x} / k = 6.01$ .

The parameters $N_{0}$ and $p$ show a relationship between stress amplitude, confining pressure, and frequency in Eq. (1). When $p =$ 1, Eq. (1) is consistent with [12] in the form, and it can be normalized.

Eq. (1) can be finally converted to:

2

G_{d} = \frac{0.83 G_{m a x}}{1 + (N / N_{0})^{p}} + 0.17 G_{m a x},

where $G_{m a x}$ is the original dynamic shear modulus.

3.2.3. Experimental analysis

Eq. (2) is used to analyze and calculate the relationship between dynamic shear modulus and the number of oscillation periods. Considering the effects of different frequencies, the results are shown in Fig. 6.

As can be seen from Fig. 6, the curve is divided into two parts. The first part experiences rapid softening; after evolving into the steady-state process, it ultimately stabilizes. There is a turning point between sharp and steady softening. The turning point corresponds to a critical number of oscillation periods. Overall, the dynamic shear modulus decreases with increasing the number of oscillation periods and increasing frequency of loads. Clay under cyclic loads produces excess pore water pressure. The effective stress of clay decreases with an increase in the number of oscillation periods that cause strain, strength, and dynamic shear modulus softening.

Fig. 6Relation curves between the dynamic shear modulus and the number of oscillation periods under different frequencies

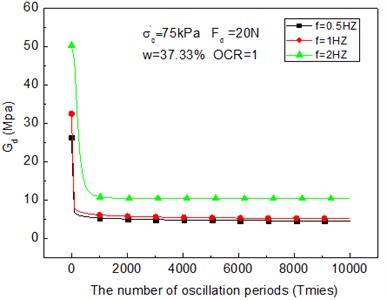
Fig. 7Predicted and test values between the dynamic shear modulus and the number of oscillation periods σA=20 kPa, σs=40 kPa, σ3=200 kPa

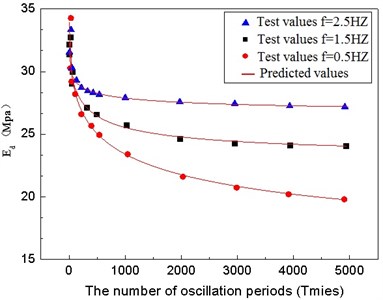
3.2.4. Recognized analysis of dynamic shear modulus function formula

The test data in [20] are verified by the recognized formula proposed in this paper. $G_{d}$ is translated by $E_{d} = G_{d} ∙ 2 (1 + μ)$ , and the parameters are shown in Table 3.

Table 3Parameters of dynamic shear modulus function formula

Confining pressure / kPa	frequency / Hz	Parameters
Confining pressure / kPa	frequency / Hz	$G_{m a x}$	$N_{0}$	$p$
200	0.5	30	352	0.45
	1.5	30.2	259	0.66
	2.5	31.6	152	0.49

The results of the previous analysis are in agreement with the test values, and indicate that the improved formula works well in projects and will likely be widely used. The formula is beneficial to analyzing the dynamic characteristics of clay.

Fig. 7 shows that the dynamic shear modulus can be divided into sharp soft stages and smooth phases. But the critical number of oscillation periods is less clearly defined and difficultly stabilized.

4. Applications in cam-clay model

Statistics show that subway field trials can be conducted with the measuring acceleration method and arranging reference points to monitor the internal soil dynamic pore pressure and soil pressure [23, 24]. The proposed improved formula can be used to evaluate the dynamic characteristics of clay about the number of oscillation periods; indoor trials also suggest that the development of the appropriate methods match the site results [25]. Dynamic shear modulus can be used to evaluate the law of the dynamic characteristics of clay [26].

4.1. Interconnection of dynamic shear modulus function and parameters for cam-clay model

When metro loads act on clay, the additional settlement arising from the operation stage of the metro can be analyzed [27]. The cam-clay model is regarded as a widely used constitutive model, but it has the following disadvantages when simulating cyclic loads [28]:

1) If the initial loading stress is greater than the yield surface on clay, it is likely to produce large plastic deformation, and the subsequent cyclic loads, as long as the current loading surface does not exceed the yield surface at this time, does not produce plastic deformation, and then the cyclic loads are taken as an elastic process.

2) Unable to consider the impact of load frequency.

In order to solve the above two problems and more effectively simulate cyclic loads, assuming the cam-clay model is studied only in a small strain range. Because $M$ has nothing to do with the stress path, it is constant and so is the initial void ratio $e_{0}$ .

$λ = 0.01 0.9$ and $κ = 0.01 0.9$ are obtained by collecting data from the literature. Based on the calculating and analyzing results, the cam-clay model parameters $λ$ , $κ$ , and the dynamic shear modulus $G_{d}$ show the following relationship [29].

According to the definition, the compression index is:

3

C_{c} = - \frac{Δ e}{Δ l o g 1 0^{p}} \approx - \frac{d e}{d (l o g 1 0^{p})} = - \frac{p}{0.434} \cdot \frac{Δ e}{Δ p} .

The coefficient of compressibility is:

4

a_{v} = - \frac{Δ e}{Δ p} .

The relation between $a_{v}$ and $C_{c}$ is found by combining Eq. (6) and (7):

5

C_{c} = a_{v} \cdot \frac{p}{0.434} .

By equation:

6

d (l o g 1 0^{p}) = \frac{1}{p} (l o g 1 0^{e}) d p = \frac{0.434 d p}{p} .

By definition:

7

a_{v} = \frac{1 + e_{0}}{E_{s}} .

The relation is:

8

E_{0} = (1 - \frac{2 μ}{1 - μ}) E_{s} = β E_{s},

where $E_{s}$ is the compress modulus with lateral confinement; $E_{0}$ is the compress modulus without lateral confinement.

After Eq. (8) is introduced into Eq. (7), then:

9

a_{v} = \frac{β (1 + e_{0})}{E_{0}} = \frac{β (1 + e_{0})}{[G_{d (l o a d)} \cdot 2 (1 + μ)]} .

The relation between $C_{c}$ and dynamic shear modulus and dynamic shear modulus $G_{d (l o a d)}$ under loading is acquired by combining Eqs. (6) and (7), where $E_{d} = G_{d} \cdot 2 (1 + μ)$ :

10

C_{c} = \frac{β (1 + e_{0}) p}{0.434 [G_{d (l o a d)} \cdot 2 (1 + μ)]} .

Similarly, the relation between $C_{c}$ and dynamic shear modulus $G_{d (u n l o a d)}$ under unloading is:

11

C_{s} = \frac{β (1 + e_{0}) p}{0.434 [G_{d (u n l o a d)} \cdot 2 (1 + μ)]} .

By the equation: $λ = 0.434 C_{c}$ and $κ = 0.434 C_{s}$ , thus:

12

λ_{d} = \frac{(1 - \frac{2 μ}{1 - μ}) (1 + e_{0}) p}{[G_{d (l o a d)} \cdot 2 (1 + μ)]},

13

κ_{d} = \frac{(1 - \frac{2 μ}{1 - μ}) (1 + e_{0}) p}{[G_{d (u n l o a d)} \cdot 2 (1 + μ)]},

where $p$ is effective stress, as can be seen from Fig. 8, and $p = A s i n x + B$ is half-sine under cyclic loads.

Fig. 8Relation curves between the effective stress and the number of oscillation periods under cyclic loads

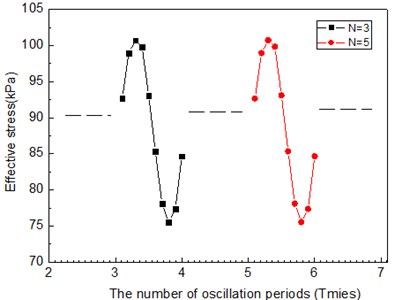
Fig. 8 illustrates the relationship between effective stress and the number of oscillation periods. As shown in the figure, cyclic loads collect 10 points in one period, where the relationship is a half-sine and periodic curve.

Computational analysis found that the formula in the small strain range shows some applicability. Among them, the parameter $ν$ has greater impact on $λ_{d}$ and $κ_{d}$ .

When loading, the changing law of cam-clay model parameters $λ_{d}$ and $κ_{d}$ with the variation of the number of oscillation periods can be calculated. The modified cam-clay model with variable parameters can be constructed [30]. Fig. 9 shows the comparison of test data and predicted values calculated by Eqs. (2), (12), (13) between the variable parameters of modified cam-clay model and the number of oscillation periods. The Fig. 9 only presents one out of every ten test values. It can be observed in the figure that the predicted values and test values are consistent.

Fig. 9Predicted and test data between the variable parameters of modified cam-clay model and the number of oscillation periods

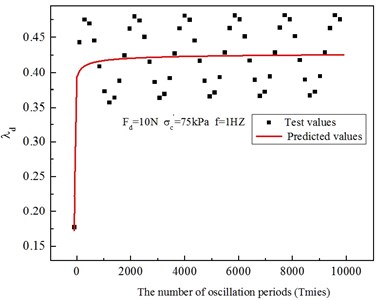
a)

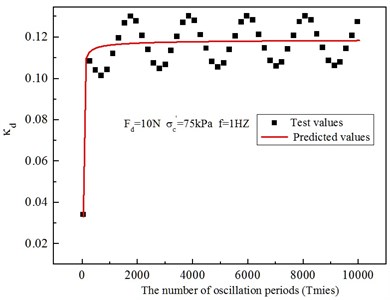
b)

Meanwhile, the parameters $λ_{d}$ and $κ_{d}$ for various frequencies are calculated. Fig. 10 shows that parameters increase along with the number of oscillation periods, it also reflects the soft soil softening phenomenon with the increasing number of oscillation periods. Because the soil is in-homogeneity material, the curve in Fig. 10 is somewhat irregular, but the regularity is also obvious. Under the same conditions, the frequency increases and the parameters ( $λ_{d}$ and $κ_{d}$ ) decreases. Model parameters that vary with the number of oscillation periods can be substituted into the cam-clay model.

Fig. 10Variable parameters of cam-clay model – the number of oscillation periods curve

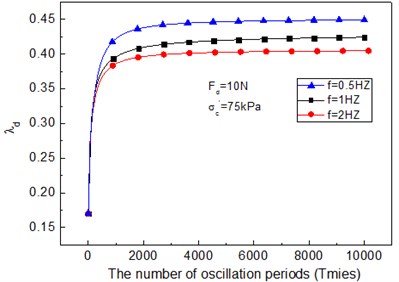
a)

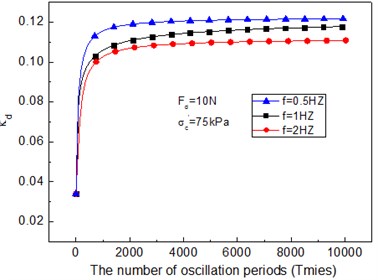
b)

The variable parameters with the number of oscillation periods are introduced into the cam-clay model. The constitutive relation of cam-clay model is described as:

14

\{\begin{array}{l} d ε_{v} \\ d ε_{d} \end{array}\} = [D^{e p}] \{\begin{array}{l} d p \\ d q \end{array}\} = \frac{1}{p} [\begin{array}{l} D_{p p} \\ D_{q p} \end{array} \begin{array}{l} D_{p q} \\ D_{q q} \end{array}] \{\begin{array}{l} d p \\ d q \end{array}\},

where:

D_{p p} = c_{κ} + c_{p} \frac{M^{2} - η^{2}}{M^{2} + η^{2}}, D_{p q} = c_{p} \frac{2 η}{M^{2} + η^{2}}, D_{q p} = c_{p} \frac{2 η}{M^{2} + η^{2}},

D_{q q} = \frac{2}{9} c_{κ} \frac{1 + ν}{1 - 2 ν} + c_{p} \frac{4 η^{2}}{M^{4} - η^{4}}, c_{κ} = \frac{κ}{1 + e_{0}}, c_{p} = \frac{λ - κ}{1 + e_{0}},

η = \frac{q}{p}, p = \frac{σ_{1} + 2 σ_{3}}{3}, q = (σ_{1} - σ_{3}) .

According to the consolidated undrained triaxial test, the $d ε_{v} = 0$ , $d ε_{3} = - d ε_{1} / 2$ can be substituted into Eq. (14).

4.2. Verification of the modified cam-clay model

In order to verify the modified cam-clay model, the dynamic triaxial test is conducted. For the sake of contrastive analysis, the data when the strain reaches the peak value are chosen. The test results of the two kinds of model simulation are compared as follows. When the cam-clay model with invariable parameter is set, the parameters are obtained through indoor CU test (consolidated undrained triaxial test) and CD test (consolidated drained triaxial test) as well as conventional indoor tests; they are: $M =$ 1.42, $e_{0} =$ 0.99, $ν =$ 0.3, $λ =$ 0.34, and $κ =$ 0.08. The predicted values are shown in Fig. 11. The test results and predicted values of the modified cam-clay model with variable parameters are shown in Fig. 12.

Fig. 11Predicted values of the cam-clay model with invariable parameter under cyclic loads

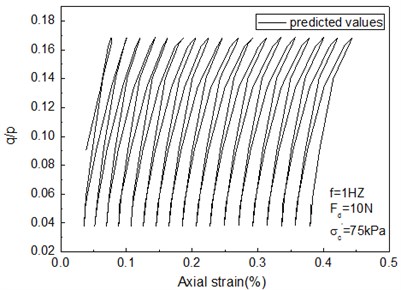
In Figs. 11-12, the $q / p$ is defined as the cyclic stress ratio. Fig. 11 shows the predicted values of the cam-clay model with invariable parameter, there is no hysteresis loop, and the influence of loading frequencies on soil stress-strain curve cannot be taken into account. In Fig. 12, the modified cam-clay model with variable parameters can not only describe the hysteresis loops of soil under cyclic loads, but also predict the effects of different loading frequencies.

Comparison of Fig. 12(a), (c), and (e) and Fig. 12(b), (d), and (f) shows that the modified cam-clay model with variable parameters can better simulate the plastic deformation of saturated clay under cyclic loads, the stress-strain relation hysteresis characteristics, and accumulation of permanent deformation. In addition, the stress-strain hysteresis loops tilt to strain axis with an increase of cycles and the secant stiffness is reduced, which is in line with the stiffness softening phenomenon.

Fig. 12Comparison between test results and predicted values of the modified cam-clay model with variable parameters under cyclic loads

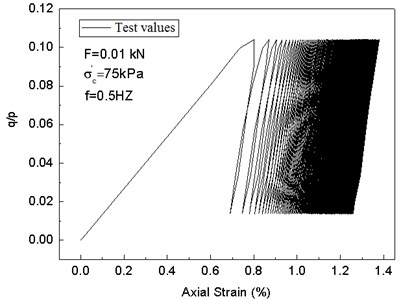
a)

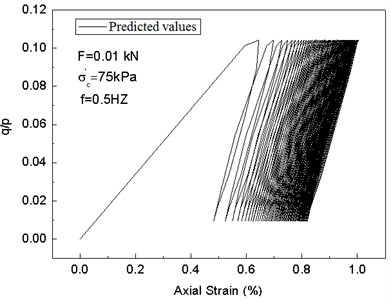
b)

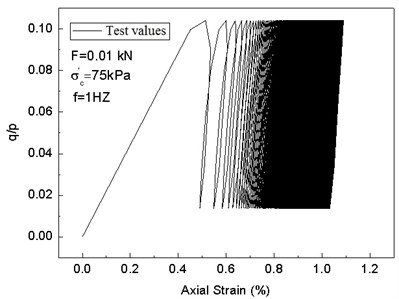
c)

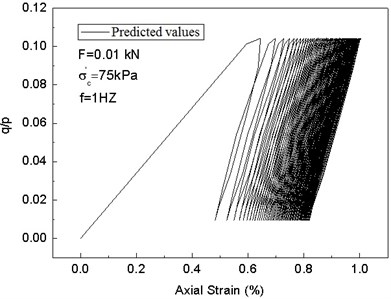
d)

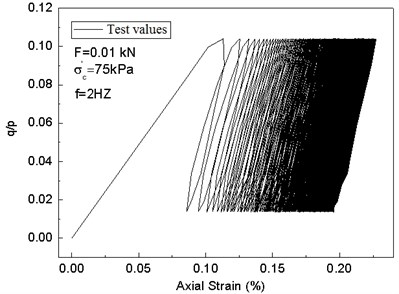
e)

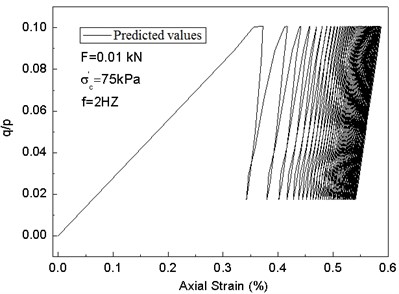
f)

4.3. Applications of the modified cam-clay model for different clays

This method can be applied to soils in different areas. This is because, based on the definitions of basic physical parameters including the compression index (Eq. (3)) and the coefficient of compressibility (Eq. (4)) of soil mechanics, the method establishes relationship among Eqs. (3) and (4). In this way, the relationship between the coefficient of compressibility and elasticity modulus can be established. Then according to $λ = 0.434 C_{c}$ and $κ = 0.434 C_{s}$ , the parameters of the cam-clay model are associated with the dynamic shear modulus.

Fig. 13(a) demonstrates the results of the dynamic triaxial test on the soil in the United States given in [31]. Fig. 13(b) shows the predicted results of the proposed method here, frequency $f =$ 1 Hz is taken into account. Apparent hysteresis loops are observed in the predicted curve and are close to the test values. This proves that the proposed method can be applied widely for calculating and analyzing the soils of different countries.

Fig. 13Comparison of test results and predicted values of the modified cam-clay model with variable parameters under cyclic loads

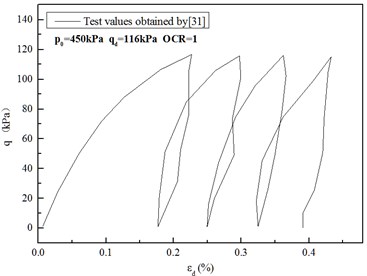
a)

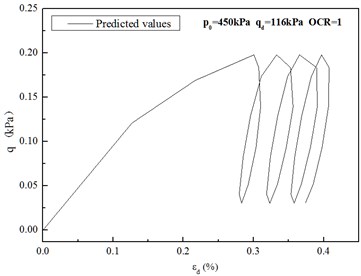
b)

5. Conclusions

In this paper, clay was analyzed using indoor GDS multi-purpose dynamic cyclic triaxial tests under consolidated undrained and stress control. The following conclusions can be obtained by analyzing the dynamic characteristics of clay:

1. A formula is constructed to calculate the dynamic shear modulus and to present the concept of stable dynamic shear modulus. Considering the effects of frequency, the data in different parts of clay can be verified. The dynamic shear modulus function formula is proven. The evaluation of dynamic characteristics of clay under metro loads by changing the number of oscillation periods is revealed.

2. By introducing the dynamic shear modulus function formula into the cam-clay model, a modified cam-clay model with variable parameters is then constructed. The modified cam-clay model can be used to overcome the problems of describing hysteresis loops by considering the effect of loading frequency on the dynamic characteristics of clay.

3. By verifying the proposed modified cam-clay model and theoretically analyzing its applicability, the results of testing soils of different countries verify that the method is effective.

References

Cui Y. J., Delage P. Yielding and plastic behaviour of an unsaturated compacted silt. Geotechnique, Vol. 46, Issue 2, 1996, p. 291-311.

Search CrossRef
Qubain Bashar S., Li Jianchao, Chang Kristen E. Cam clay-coupled consolidation analysis of field instrumented preloading program. Journal of Geotechnical and Geoenvironmental Engineering, Vol. 140, Issue 4, 2014.

Search CrossRef
Zhang Jun-Feng, Chen Jin-Jian, Wang Jian-Hua Prediction of tunnel displacement induced by adjacent excavation in soft soil. Tunneling and Underground Space Technology, Vol. 36, 2013, p. 24-33.

Search CrossRef
Hardin B. O., Drnevich V. P. Shear modulus and damping in soils: design equations and curves. Journal of the Soil Mechanics and Foundations Division, Vol. 98, Issue 7, 1972, p. 667-692.

Search CrossRef
Isao Ishibash Unified dynamic shear moduli and damping ratios of sand and clay. Soil and Foundation, Vol. 33, Issue 1, 1993, p. 182-191.

Search CrossRef
Li X. S., Cai Z. Y. Effects of low-number previbration cycles on dynamic properties of dry sand. Journal of Geotechnical and Geoenvironmental Engineering, Vol. 125, Issue 11, 1999, p. 979-987.

Search CrossRef
Wichtmann T., Triantafyllidis Th. Influence of a cyclic and cyclic loading history on dynamic properties of dry sand, part I: cyclic and dynamic torsional prestraining. Soil Dynamics and Earthquake Engineering, Vol. 24, Issue 2, 2004, p. 127-147.

Search CrossRef
Wichtmann T., Triantafyllidis Th. Influence of a cyclic and cyclic loading history on dynamic properties of dry sand, part II: cyclic axial preloading. Soil Dynamics and Earthquake Engineering, Vol. 24, Issue 11, 2004, p. 789-803.

Search CrossRef
Wichtmann T., Triantafyllidis T. Effect of uniformity coefficient on G/Gmax and damping ratio of uniform to well-graded quartz sands. Journal of Geotechnical and Geoenvironmental Engineering, Vol. 139, Issue 1, 2012, p. 59-72.

Search CrossRef
Subramaniam P., Banerjee Sunbhadeep Shear modulus degradation model for cohesive soils. Soil Dynamics and Earthquake Engineering, Vol. 53, 2013, p. 210-216.

Search CrossRef
Pavlenko Olga V. Nonlinear seismic effects in soils numerical simulation and study. Bulletin of the Seismological Society of America, Vol. 91, Issue 2, 2001, p. 381-396.

Search CrossRef
Hardin Bobby O., Blandford George E. Elasticity of particulate materials. Journal of the Geotechnical Engineering, Vol. 115, Issue 6, 1989, p. 788-805.

Search CrossRef
Hardin Bobby O., Kalinski Michael E. Estimating the shear modulus of gravelly soils. Journal of Geotechnical and Geoenvironmental Engineering, Vol. 131, Issue 7, 2005, p. 867-875.

Search CrossRef
Idriss I. M., Dobry R., Singh R. D. Nonlinear behavior of soft clays during cyclic loads conditions Journal of the Geotechnical Engineering, Vol. 26, 1978, p. 1427-1447.

Search CrossRef
Narasimha Rao S., Panda A. P. Non-linear analysis of undrained cyclic strength of soft marine clay. Ocean Engineering, Vol. 26, Issue 3, 1999, p. 241-253.

Search CrossRef
Wang Jun, Cai Yuan Qiang, Yang Fang Effects of initial shear stress on cyclic behavior of saturated soft cla. Marine Georesources and Geotechnology, Vol. 31, Issue 1, 2013, p. 86-106.

Search CrossRef
Wood D. M. Soil Behavior and Critical Soil Mechanics. Cambridge University Press, 1990.

Search CrossRef
He Zhen-jun, Zhang Jia-xing Strength characteristics and failure criterion of plain recycled aggregate concrete under triaxial stress states. Construction and Building Materials, Vol. 54, 2014, p. 354-362.

Search CrossRef
Alpan I. The geotechnical properties of soils. Earth-Science Reviews, Vol. 6, Issue 1, 1970, p. 5-49.

Search CrossRef
Xu Yiqing, Tang Yiqun Experimental study on dynamic elastic modulus of reinforced soft clay around subway tunnel under vibration loading. Engineering Mechanics, Vol. 29, Issue 7, 2012, p. 250-269.

Search CrossRef
Yasuhara Kazuya, Hyde Adrian F. L. Method for estimating post-cyclic undrained secant modulus of clays. Journal of Geotechnical and Geo-environmental engineering, Vol. 123, Issue 3, 1997, p. 204-211.

Search CrossRef
Yasuhara Kazuya Post-cyclic undrained strength for cohesive soils. Journal of Geotechnical Engineering, Vol. 120, Issue 11, 1994.

Search CrossRef
Zhang Jun-Feng, Chen Jin-Jian, Wang Jian-Hug Prediction of tunnel displacement induced by adjacent excavation in soft soil. Tunneling and Underground Space Technology, Vol. 36, 2013, p. 24-33.

Search CrossRef
Shen Shui-Long, Wu Huai-Na, Cui Yu-Jun Long-term settlement behaviour of metro tunnels in the soft deposits of Shanghai. Tunneling and Underground Space Technology, Vol. 40, 2014, p. 309-323.

Search CrossRef
Ng C. W. W., Liu G. B., Li Q. Investigation of the long-term tunnel settlement mechanisms of the first metro line in Shanghai. Canadian Geotechnical Journal, Vol. 50, Issue 6, 2013, p. 674-684.

Search CrossRef
Tan Yong, Wang Dalong Characteristics of a large-scale deep foundation pit excavated by the Central-Island technique in Shanghai Soft Clay. I: Bottom-up construction of the central cylindrical shaft. Journal of Geotechnical and Geoenvironmental Engineering, Vol. 139, Issue 11, 2013, p. 1875-1893.

Search CrossRef
Tan Yong, Wang Dalong Characteristics of a large-scale deep foundation pit excavated by the Central-Island technique in Shanghai Soft Clay. II: Top-down construction of the peripheral rectangular pit. Journal of Geotechnical and Geoenvironmental Engineering, Vol. 139, Issue 11, 2013, p. 1894-1910.

Search CrossRef
Mašín D. Hypoplastic cam-clay model. Geotechnique, Vol. 62, Issue 6, 2012, p. 549-553.

Search CrossRef
Donald G. Jorgensen Relationships between Basic Soils-Engineering Equations and Basic Ground-Water Flow Equations. United States Government Printing Office, Washington, 1980.

Search CrossRef
Mašín D. A hypoplastic constitutive model for clays. International Journal for Numerical and Analytical Methods in Geomechanics, Vol. 29, Issue 4, 2005, p. 311-336.

Search CrossRef
Li Tao, Meissner Helmut Two-surface plasticity model for cyclic undrained behavior of clays. Journal of Geotechnical and Geoenvironmental Engineering, Vol. 128, Issue 7, 2002.

Search CrossRef

About this article

Received

18 September 2014

Accepted

13 January 2015

Published

15 February 2015

SUBJECTS

Mechanical vibrations and applications

Keywords

clay

cyclic loads

dynamic triaxial test

dynamic characteristics

dynamic shear modulus

Acknowledgements

The authors gratefully acknowledge the financial support for this research from the National Natural Science Foundation of China (Grant Nos. 51278099), Postgraduate Research and Innovation Plan Project in Jiangsu Province (Grant Nos. CXLX13_098). We thank LetPub (www.letpub.com) for its linguistic assistance during the preparation of this manuscript.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.