Abstract
This paper proposes an automatic diagnostic scheme without manual feature extraction or signal pre-processing. It directly handles the original data from sensors and determines the condition of the rolling bearing. With proper application of the new technique of shift invariant sparse coding (SISC), it is much easier to recognize the fault. Yet, this SISC, though being a powerful machine learning algorithm to train and test the original signals, is quite demanding computationally. Therefore, this paper proposes a highly efficient SISC which has been proved by experiments to be capable of representing signals better and making converges faster. For better performance, the AdaBoost algorithm is also combined with SISC classifier. Validated by the fault diagnosis of bearings and compared with other methods, this algorithm has higher accuracy rate and is more robust to load as well as to certain variation of speed.
1. Introduction
Traditional fault diagnosis procedure contains signal pre-processing, feature extraction, feature selection and pattern recognition [1]. Many approaches have been developed for different machines, and much success has also been achieved in machinery fault diagnosis [2]. However, due to the complicate steps and a large number of parameters to setting, it involves sufficient professional knowledge and experience. When the fault mechanism of the new equipment is unknown, or when the worker lacks experience, it will be a challenge to diagnose the rolling bearing efficiently. Therefore, a desirable diagnostic system should be able to automate the fault detection process without requiring any prior knowledge, so that it can be easily used even by those without experience [3]. In order to automate fault recognition and satisfy the demand for high accuracy, this paper designed a diagnostic scheme with the help of some improved machine learning algorithms.
When mechanical fault features are weak or relatively similar, it is hard to achieve condition monitor through traditional signal processing or pattern recognition techniques. Recently, sparse coding evolving from compress sensing has been a fundamental and effective technique in such fields as neurology, signal processing and pattern recognition [4, 5]. It represents signals as sparse linear combination of over complete bases, and achieves the simplest signal representation through the adaptive learning of the best bases and coefficients. This automatic learning algorithm does not require manual selection of features, and the features learned from original signals tend to represent the essence of signals [5]. Sparse coding is also a robust and adaptive pattern recognition algorithm [6]. Sparse coding for pattern recognition has been successfully applied in many fields such as face recognition and sound processing [7].
Due to the fact that the feature in the section of a signal may locate at any time, it is necessary to use many bases to represent the same feature for conventional sparse coding. The technique of shift invariant sparse coding (SISC) [8, 9] could represent such features sparsely, which describes a signal as the convolutions of bases and coefficients. Liu [10] is the first to apply SISC to rolling bearing fault diagnosis for feature extraction, and to demonstrate that its accuracy, robustness and adaptability are superior to traditional diagnostic methods. Tang [11] used SISC to find out and extract, at the early failure stage, the latent fault features which are submerged or distorted by relatively strong background noise. Therefore, it can be reasoned that SISC is an excellent approach to feature extraction for fault detection.
However, some drawbacks still exist in practical application for SISC. Due to the convolution of bases and coefficients, SISC adds a dimension to the coefficient matrix compared to conventional sparse coding, and thus increases computation in solving the best coefficients and bases. Conventional approaches for solving SISC may easily be trapped into local optimal solution. In such case, an efficient SISC with better performance is necessary. Therefore, this paper proposes an improved shift invariant sparse coding (ISISC). In dictionary learning procedure, the optimum problem is simplified into a small linear equation, and thus can be solved directly by Cholesky decomposition. What’s more, an improved orthogonal matching pursuit (OMP) and an online learning algorithm are also adopted for higher efficiency.
In practice of fault diagnosis, the normal and abnormal signals are very similar at the early failure stage. The strong background noise and variety of operating condition lead to more latent discriminating features, which requires that the performance of machine learning method for fault diagnosis be enhanced as much as possible, and that the classifiable ability of SISC be further improved. In order to improve the classifiable performance of conventional sparse coding, some researchers add discrimination constraint to the sparsity in dictionary learning process [7], so that the same classes have similar sparse codes and different classes have discriminating codes. But this method will make some fast dictionary learning algorithm unavailable and the optimization no longer convex. Ensemble learning is an accepted effective algorithm of machine learning [12], and AdaBoost algorithm [13] is a valid approach to ensemble learning. AdaBoost algorithm does not change the optimization function of ISISC, therefore, this paper introduces AdaBoost algorithm into ISISC for better pattern recognition.
2. ISISC ensemble
2.1. Introduction of SISC
In the theory of SISC [9], by using an over complete dictionary matrix which contains prototype bases for columns, a signal can be represented as the sum of the convolutions of these bases and coefficients:
where indicates convolution, coding coefficient is sparse, is a normalized Gaussian noise, , , and .
To make the optimization convex, the basis and coefficient are optimized repeatedly. The cost function for evaluating the representation of the signal set containing signals is as follows [14]:
where is norm, is a parameter, which determines the degree of sparsity. The basis needs to be normalized, namely . If and are solved at the same time, then the optimization problem is no-convex, making it more difficult to get a stable and convergent solution. As a result, the basis and coefficient are optimized iteratively and repeatedly according to the maximum posterior probability estimation until convergence. Many experiments have validated this approach as highly effective [4]. Many scholars have studied how to solve and simplify this problem. Smith [9] and Blumensath [8] proposed the most common optimization procedure. They directly updated the bases based on gradients, and successfully employed this way in voice and music processing. Grosse [14] and Tang [11] transformed signals into frequency domain, and used the gradients to solve the optimal bases. The gradient-based SISC (GSISC) method by Smith and Blumensath is as follows:
Let , the derivation of a given cost function with respect to the th element of basis is [8, 9]:
where , , .
Similarly, the derivation of a given cost function with respect to the th element of coefficient vector is as [8, 9]:
where , .
After using the gradients in Eq. (3) and (4) to optimize the bases and coefficients iteratively until convergence is reached, the original signals can be sparsely represented by learned bases and coefficients. Besides, the coding coefficients could be also solved by OMP, FOCUSS algorithm, etc. As outlined above, the gradients used in these optimization algorithms are estimated through the numerical difference, and so the exact step length per iteration is hard to be taken, and the best evaluation in each iteration shall not guaranteed.
2.2. The procedure of ISISC
The efficient K-SVD algorithm [4] updates the bases one by one, rather than all at once. Inspired by this idea, the bases of ISISC are also updated one by one in the dictionary learning process. First, due to the sparsity of coefficients, the nonzero coefficients are extracted to markedly reduce the scale of the optimization problem. Then, the convolution problem is converted into a small scale symmetric positive linear equation, which can be directly solved by Cholesky algorithm without being influenced by former iterative result. So this scheme converges faster than GSISC. In the coefficient update stage, higher efficiency is achieved by the employment of OMP, fast convolution algorithm and extraction of only nonzero coefficients.
2.2.1. Dictionary update
In dictionary updating phase the coefficients are unchanged, and only the bases are updated. The cost function is simplified as:
where the matrix stands for the error of all the bases except the th basis with respect to the th signal.
Here is introduction on how to convert updating into solving a linear equation with regard to . Because , the optimum problem with only the th signal is analyzed first. The optimization of Eq. (5) equals to the solution of Eq. (6):
If the left matrix of Eq. (6) is taken as a special Toeplitz matrix with regard to coefficient , then Eq. (6) can be rewritten as . In view of the sparsity of coefficient , many rows in the matrix are all zeros and these zero rows have no effect on the update of bases. Delete these zero rows from matrix and those corresponding rows in matrix , then Eq. (6) can be rewritten as . When all the signals are taken consideration, the optimization of the cost function is represented as:
When Eq. (7) is abbreviated as , and based on the least square method, the updated basis can be obtained as . Because matrix , and in general, the above equation is transformed into a small scale of linear equation, which can be directly solved by Cholesky factorization, or LU factorization for the optimal value. In theory, during the process of dictionary learning, the update relation of basis given in Eq. (7) is the best that can be achieved provided that coefficients and other bases are fixed, and the solution will not affected by the former iterative result. But since it is hard to choose the step length accurately, GSISC converged relatively slower, and the update is affected by the former iterative result.
All the bases are randomly updated one by one so as to get the best solution of the basis in this round. Afterwards each basis is normalized as .
2.2.2. Shift invariant OMP
OMP is chosen to solve the coding coefficients, and in this process all the bases are fixed, so that only the coefficients are optimized. As a new version of matching pursuit, OMP is also an iterative greedy algorithm [15]. After choosing the best suitable basis in each iteration, OMP would make all the bases to be orthogonal to each other and project them on the original signal again.
The points translation of the basis is padded with zeros so that the new basis is as long as original signal, which is represented as , and . is the over complete dictionary for sparse representation. The procedure of shift invariant OMP is as follows [15]:
(1) Set as the signal for representation, initialize the index set , the iteration counter , and the residual .
(2) Find the index of the basis that satisfies:
The fast convolution can be applied for fast calculation when calculating .
(3) Augment the matrix of chosen bases: .
(4) Because of the sparsity of the chosen bases (namely column vectors), the matrix has many rows composed of zeros. The nonzero rows of matrix are extracted from original matrix , and the corresponding elements of signal are extracted as the vector . This technique will significantly reduce the size of the matrix and enhance the efficiency. According to the least square method, the coefficients are estimated: , and the residual is .
(5) Increment , and return to Step 2 if is smaller than the maximum iterations. Otherwise output the estimated reconstructed signal and its residual .
In addition, the procedure can also be accelerated by batch-OMP [16] for more efficiency. Worked with proposed OMP, the sparse coding will be evaluated at an extremely faster speed.
2.2.3. Online learning
Mairal [17] is the first to introduce online learning to sparse coding to increase the computational speed. Tang [11] applied this method to SISC. In Tang’s algorithm, the dictionary is updated only by one sample in each iteration, causing the dictionary to match only the current sample well and easily leading to local optimal solution. This paper proposes a new online learning algorithm to overcome this shortcoming.
Step 1, divide the training sample set into small sub sets, and the th sub set is . The iteration number , the candidate training set is null set. Initiate the dictionary randomly.
Step 2, let , and .
Step 3, update the coefficients by shift invariant OMP of all the samples in .
Step 4, update the dictionary by ISISC, using all the samples in .
Step 5, if , go to step 6, otherwise go to step 2.
Step 6, let , using all the samples to update the coefficients with shift invariant OMP, and update the dictionary by ISISC.
Step 7, if equals the max iteration number, output the trained dictionary, otherwise go to step 6.
While applying the algorithm above, it is necessary to just use few samples to update the dictionary for faster convergence, because the dictionary is far from the best dictionary in the former phase. However, in the later phase, if only few samples are used, it may get trapped in local optimal solution, hence much more samples are applied for fine tuning.
2.3. SISC ensemble for pattern recognition
Sparse coding and pattern recognition have natural relationship [6]. Under the limitation of sparsity, the most closely related basis with the original signal will be automatically selected, and the other bases are refused. The robustness and accuracy of sparse coding for pattern recognition have been validated in the field of face recognition and voice processing. The original dictionary can be constructed directly by selecting some training samples, and can be learned through dictionary learning algorithm. Dictionary learning [5] is able to learn the internal structures and main features of original signals through a group of sparse bases, and it is insensitive to Gaussian noise. In this paper, the ISISC proposed in Section 2.2 is used for dictionary learning, and one sub dictionary per class is learned.
In this investigation, the sub dictionaries are not combined together in order to avoid destroying the structure of each sub dictionary. But under the same sparsity of , each sub dictionary is employed respectively for sparse representation. When the label of the sample and the label of the sub dictionary are the same, the reconstruction error should be the lowest, which means that the label of the dictionary with lowest reconstruction error is expected to be the label of the sample.
Unfortunately, real-world vibration signals are often contaminated by a lot of noise, and the number of available training sample is limited. Thus it is necessary to further improve the classification ability of sparse coding. Some scholars added distinctive constraints to sparsity when training dictionary so that the dictionaries can be more discerning. However, this approach will increases the difficulty of optimization and make some fast algorithm potentially unable to work well, or even make convergence unstable. Ensemble learning introduced in recent years is a very powerful machine learning method [12]. It synthesizes a few different classifiers, and can get better performance than the individual classifier that composes it. AdaBoost algorithm [13], proposed by Freund and Schapire, is a valid approach to ensemble learning. The same group of training samples are used, but the weights of samples are adaptively changed after a classifier is trained. Therefore, the error sample will be paid more attention by the next classifier. Lastly the combination of classifiers, whose individual decisions are weighted by voting, will exhibit better performance. It has been verified that when the error of individual classifier is lower than 50 %, the error of combination will descend exponentially close to zero [13].
Although the sparse coding is not the same as conventional classifiers, the increase in the weight of an error sample will enhance its ability to recognize the pattern of a sample. The rise of a sample’s weight will result in the fact that the structure of the sub-dictionary learned is closer to the error sample. That is to say, the dictionary has superior ability to represent this sample, while keeping other sub-dictionaries representative ability unchanged. Therefore the reconstruction error of the sample by the new weighted sub-dictionary is relatively decreased, and the probability of being categorized as required is increased. The algorithm of ISISC ensemble is presented in Table 1 [18].
Table 1Proposed algorithm of ISISC ensemble
AdaBoost (S, ISISC, T) Input: , training sample set. Each class has training samples with labels . ISISC, the base-learning algorithm. , the number of ISISC ensemble. Initialize: the weight of sample as , 0, 0. Do while and 0.5. 1. Normalize the weights: . 2. Train the th ISISC classifier with adaptive updated weights, and recognize all the training samples. If the sample is right, namely , then 0, otherwise 1. 3. Calculate , and let . 4. Update the weight as: . 5. Increment the count number: . Output: the synthesis of all the classifiers decisions: , where is true 1, otherwise 0. |
This paper fused the AdaBoost algorithm into ISISC to enhance the successful rate for recognition faults, and the diagnostic procedure is shown in Fig. 1. The signals under different loads have diverse energies. By normalizing them, it is able to guarantee that the relative weights of samples are identical. The sub-dictionary is trained by ISISC, one for each class, in sequence according to the labels. After the first classifier was trained, and the weights of all training samples are then updated according to the method demonstrated in Table 1. Subsequently the sub-dictionaries of the next classifier are trained. Following this way, all the ISISC classifiers are to be trained. For an unlabeled sample, firstly, it is to be reconstructed under sparsity respectively by using each sub dictionary of the first classifier; secondly, it is to be classified based on the minimum reconstruction error. In such way, the sample is identified by all the ISISC classifiers. Eventually all the decisions are synthesized for the final judgment in the light of the weighted algorithm in Table 1.
Fig. 1ISISC ensemble procedure
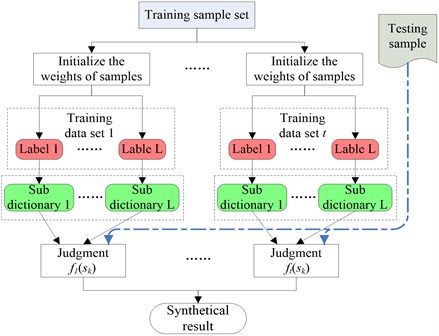
3. Experiment analysis and discussion
3.1. Comparison between ISISC and GSISC
A simulated pulse sequence of vibration signal caused by a single point defect on rolling bearing is as follows:
where is time, has a damped sinusoids function and its amplitude is modulated by a sinusoids function. is the count number of pulses, is the beginning time of pulse. Here is set as a random number in order to test the adaptability of SISC. is the period of the pulses, and here it equals 120 points. The attached noise is Gaussian noise, and its signal to noise ratio (SNR) is –2 dB. is a pulse resonance induced by the single point defect, and it is normalized in this study. is the damping coefficient, and is oscillation frequency, which indicates the damped natural frequency of the system.
The signal has 10240 points, and it is averagely separated into ten samples. GSISC and ISISC are respectively used to represent the signal set for comparison. The length of a basis is set as 60 points, and only one basis is learned. For GSISC optimization, the conjugate gradient method is chosen, and the step length is determined by both the golden section search and parabolic interpolation. The sparsity is set as 9 in ISISC, and the online learning algorithm is not adopted in this experiment.
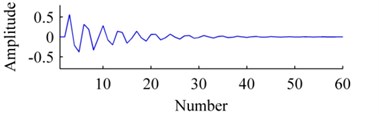
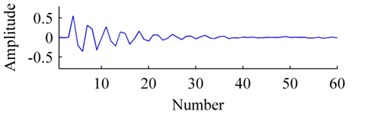
The convergence curves of residual energy is shown in Fig. 2. The original basis, the bases learned by ISISC and GSISC are illustrated in Fig. 3. ISISC converges to the optimal solution within a few iterations, and its learned basis resembles the original pulse resonance. Yet, GSISC converges considerably slowly, and its solution is slightly worse than that of ISISC. Moreover, there is a little distortion with its learned basis.
Fig. 2Residual energy
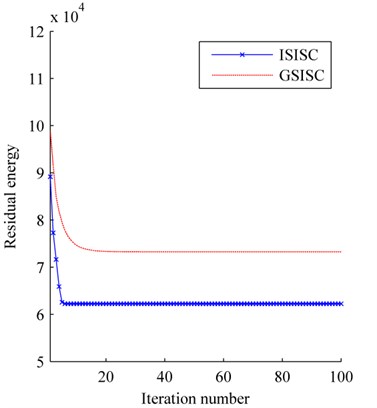
Fig. 3Bases: a) origin, b) ISISC, c) GSISC
a)
b)
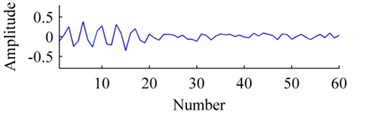
c)
Fig. 4The signal: a) origin, b) added with noises, c) ISISC, d) GSISC
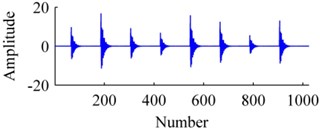
a)
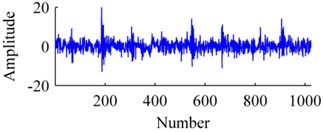
b)
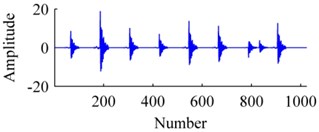
c)
d)
Fig. 4 displays an original sample, and corresponding reconstructions by ISISC, GSISC. The signal is seriously contaminated by noises, but ISISC still excellently recovers it. Unlike ISISC, the reconstruction of GSISC distorts and contains a few noises, and the peaks of pulses are not well preserved.
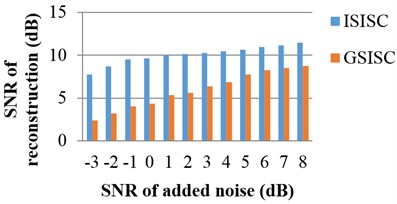
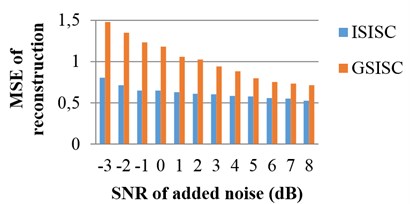
To comprehensively appraise the performances of these two algorithms, the original signals are mounted with noises of different SNR values. The SNR and MSE values of the 100th iteration are applied for evaluation. Fig. 5 shows the average results of ten times. No matter how many noises added to the original signals, ISISC always outperforms GSISC in both SNR and MSE. In contrast to GSISC and in consideration of the new dictionary updated algorithm and the experiment, ISISC is more efficient, exhibits faster convergence, is not as easy to fall into local optima, and has higher probability to find better optimal solution.
3.2. Application of ISISC ensemble to mechanical fault diagnosis
Rolling bearing is one of the most widely used elements in machinery, and its status is vital to the whole system. The database used in this paper is obtained from the Case Western Reserve University Bearing Data Center [19], which is considered as a benchmark for machinery diagnosis. Single point faults with diameters of 0.007, 0.014, 0.021 and 0.028 inches (1 inch2.54 cm) are introduced separately at the outer race (at 6:00 directions), inner race and ball. Tests are carried out respectively under loads of 0, 1, 2, 3 hp (1 hp 746 W), with corresponding shaft speed being 1797, 1772, 1750, 1730 rpm. The sampling frequency is 12 kHz. In order to determine the location and the severity of the fault, the data are divided into 10 classes, and each class contains four data with the loads of 0, 1, 2, 3 hp. The relationship between labels and data is shown in Table 2. Normal indicates the bearing is Normal. IR, B and OR respectively represent the inner race fault, ball fault and outer race fault. The number followed suggests the fault severity. For example, OR007 represents the outer race of the bearing is fault, and the fault diameter is 0.007 inch.
Fig. 5The performances of ISISC and GSISC with different noises
a) SNR of reconstruction
b) MSE of reconstruction
Table 2The relationship between data and labels
Data | Normal | IR007 | B007 | OR007 | IR014 | B014 | OR014 | IR021 | OR021 | IR028 |
Label | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Every data is truncated into time-series with a 2048-point window block. About 118 samples are generated from each data of normal condition, while each data under faulty condition contains approximately 59 samples. The ISISC ensemble proposes in this report is used to train and test the data. The number of classifiers in ensemble is five; each sub dictionary for one class contains 15 bases, and the sparsity is 26. The length of a basis is 150 points, and as its length will contain about 2 pulses in one basis, the basis will include not only the underlying information of resonance but also the fault feature frequency of each condition.
Liu [10] has applied this data set, employed SISC for feature extraction, and designed a linear classifier for identification. In his experiment, all the samples are smoothed for pre-processing. For the purpose of confirming the advantage of ISISC ensemble, two similar experiments are conducted. In the first experiment, 20 samples per data under every load are randomly selected as training set, and all the samples in the database are tested. This experiment is implemented by ISISC ensemble. The single ISISC classifier is also tested, only using 25 samples per each data for training. In Liu’s experiment [10], half samples in each data are trained which is more than either ISISC ensemble or ISISC classifier. The average accuracy rate of 0-3 hp for each class is shown in Fig. 6.
Although ISISC ensemble uses the least training samples, its success rates are highest and stable in general. This demonstrates that ISISC ensemble can accurately determine the condition of bearing as well as fault severity. Moreover, ISISC classifier and ISISC ensemble both perform better than Liu’s method on the whole. Apart from that, the efficiency has been markedly improved. Using a laptop with a dual-core 2.2 GHz CPU and DDR 667 2G memory, the training time of one class using Liu’s method is approximately one hour, whereas the time of ISISC ensemble is about ten minutes and the time of ISISC classifier is as few as 2 minutes. In comparison with Liu’s method of adding a classifier for recognition and pre-processing the samples, all the samples can be directly put into ISISC ensemble for fault recognition without any people’s operation. Dong [20] employed principal components analysis to extract features which were input into Morlet kernel support vector machine for classification. He recognized the same data of Normal, IR007, IR014, IR021 and IR028, with the accuracy rates are all as high as 100 % under the best parameters. By contrast, the accuracy rates of these data using ISISC ensemble are also 100 %, but the classes of ISISC ensemble are 10 which is more than that of Dong’s experiment.
Fig. 6The average accuracy rate of 0-3 hp for each class
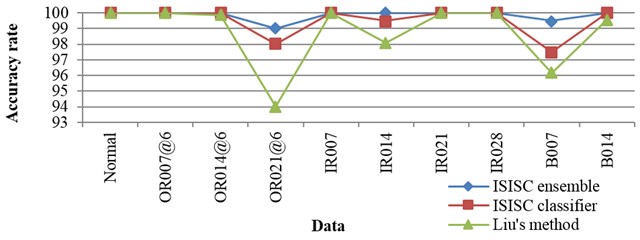
Fig. 7The accuracy rates of each data under 0-3 hp
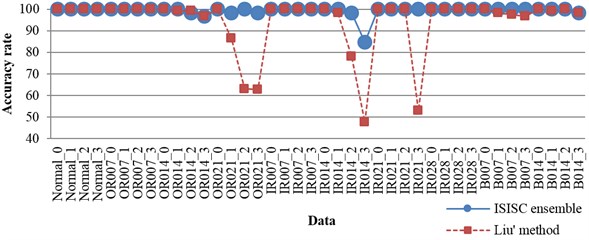
When the rolling bearing is running, its load frequently varies. The rolling bearing can hardly run at an accurate speed, and the speed usually varies in a small range. Therefore, the monitoring system needs to be robust enough against the alteration of load and the variation of speed within a small range. So another experiment is done, with only the data under 0 hp selected for training and the corresponding speed being 1797 rpm. In the training set, 50 samples per class are randomly chosen. All the data are selected for testing, namely all the data under 0, 1, 2, 3 hp, and corresponding speeds are 1797, 1772, 1750, 1730 rpm respectively. Liu [10] has also done the similar experiment, and the results of our experiment together with those of Liu’s are listed in detail in Fig. 7. The accuracy rates of ISISC ensemble are higher than Liu’s for all the data. The worst one of our method is above 80 %, while Liu’s worst rate is below 50 %, so the stability of ISISC ensemble is stronger. Zhu [2] has applied K-SVD based on envelope spectrum to do similar experiment, but he’s algorithm need to re-sample the data, so it was not robust enough to speed.
As mentioned above, it is evident that ISISC ensemble is more accurate than other methods. Apart from that, the most outstanding advantage of ISISC ensemble is that it lessens people’s participation and is much easy for application. The signal pre-processing, feature extraction and pattern recognize are not needed in this algorithm, and all the learning processes are implemented by computer itself. ISISC ensemble can still make precise judgment even when the load varies or the speed changes in a certain range.
4. Conclusions
This paper presents an intelligent diagnostic scheme based on improved SISC algorithm, and AdaBoost algorithm. This ISISC ensemble directly analyzes the original signal measured from sensors, and does not involve such technique as pre-processing, feature extraction, feature selection and so on. This diagnosis scheme is simple and demands less people’s manipulation, thus avoiding subjective operation. In order to improve the efficiency and performance of conventional SISC algorithm, the proposed ISISC transforms the complicated dictionary update into solving a small linear equation. In addition, a shift invariant OMP and an online learning algorithm are further applied for accelerating convergence. Tested by simulated signals, ISISC has faster convergence speed and can achieve better solution than GSISC.
Finally, ISISC ensemble is applied to the diagnosis of bearings, and a comparison with other researches is attached. The experiments confirm that ISISC ensemble performs better than a single ISISC classifier. Compared to other approaches, ISISC ensemble improves the accuracy rate, and can also precisely determine the fault location as well as fault severity of bearings. In addition, it is robust to the load or the speed variation in a certain range. In conclusion, ISISC ensemble facilitates the diagnostic task, and has certain value for rolling bearing diagnosis.
References
-
Hong H., Liang M. Fault severity assessment for rolling element bearings using the Lempel-Ziv complexity and continuous wavelet transform. Journal of Sound and Vibration, Vol. 320, Issue 1, 2009, p. 452-468.
-
Zhu H., Wang X., Zhao Y., et al. Sparse representation based on adaptive multiscale features for robust machinery fault diagnosis. Proceedings of the Institution of Mechanical Engineers, Part C, Journal of Mechanical Engineering Science, 2014.
-
Kankar P., Sharma S. C., Harsha S. Fault diagnosis of ball bearings using machine learning methods. Expert Systems with Applications, Vol. 38, Issue 3, 2011, p. 1876-1886.
-
Aharon M., Elad M., Bruckstein A. K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation. IEEE Transactions on Signal Processing, Vol. 54, Issue 11, 2006, p. 4311-4322.
-
Olshausen B. A. Emergence of simple-cell receptive field properties by learning a sparse code for natural images. Nature, Vol. 381, Issue 6583, 1996, p. 607-609.
-
Wright J., Yang A. Y., Ganesh A., et al. Robust face recognition via sparse representation. IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 31, Issue 2, 2009, p. 210-227.
-
Jiang Z., Lin Z., Davis L. S. Learning a discriminative dictionary for sparse coding via label consistent K-SVD. IEEE Conference on Computer Vision and Pattern Recognition, 2011, p. 1697-1704.
-
Blumensath T., Davies M. Sparse and shift-invariant representations of music. IEEE Transactions on Audio, Speech, and Language Processing, Vol. 14, Issue 1, 2006, p. 50-57.
-
Smith E. C., Lewicki M. S. Efficient auditory coding. Nature, Vol. 439, Issue 7079, 2006, p. 978-982.
-
Liu H., Liu C., Huang Y. Adaptive feature extraction using sparse coding for machinery fault diagnosis. Mechanical Systems and Signal Processing, Vol. 25, Issue 2, 2011, p. 558-574.
-
Tang H., Chen J., Dong G. Sparse representation based latent components analysis for machinery weak fault detection. Mechanical Systems and Signal Processing, Vol. 46, Issue 2, 2014, p. 373-388.
-
Polikar R. Ensemble based systems in decision making. IEEE Circuits and Systems Magazine, Vol. 6, Issue 3, 2006, p. 21-45.
-
Freund Y., Schapire R. E. A decision-theoretic generalization of on-line learning and an application to boosting. Journal of Computer and System Sciences, Vol. 55, Issue 1, 1997, p. 119-139.
-
Grosse R., Raina R., Kwong H., et al. Shift-invariance sparse coding for audio classification. Conference on Uncertainty in AI, 2007.
-
Pati Y. C., Rezaiifar R., Krishnaprasad P. Orthogonal matching pursuit: recursive function approximation with applications to wavelet decomposition. IEEE The Twenty-Seventh Asilomar Conference on Signals, Systems and Computers, Vol. 1, 1993, p. 40-44.
-
Rubinstein R., Zibulevsky M., Elad M. Efficient implementation of the K-SVD algorithm using batch orthogonal matching pursuit. CS Technion, Vol. 40, Issue 8, 2008, p. 40.
-
Mairal J., Bach F., Ponce J., et al. Online learning for matrix factorization and sparse coding. The Journal of Machine Learning Research, Vol. 11, 2010, p. 19-60.
-
Hu Q., He Z., Zhang Z., et al. Fault diagnosis of rotating machinery based on improved wavelet package transform and SVMs ensemble. Mechanical Systems and Signal Processing, Vol. 21, Issue 2, 2007, p. 688-705.
-
Loparo K. A. Bearing vibration dataset. Case Western Reserve University, http://www.eecs.cwru.edu/laboratory/bearing/download.htm, 2003.
-
Dong S., Sun D., Tang B., et al. A fault diagnosis method for rotating machinery based on PCA and morlet kernel SVM. Mathematical Problems in Engineering, Vol. 2014, 2014, p. 8.
About this article
This work was supported by the National Natural Science Foundation of China under Grant No. 61472444, 61472392.
