Influence of ventilation on flow-induced vibration of rope-guided conveyance

2.1. Mathematical model

Fig. 1 gives the mathematical model of rope-guided hoisting system. According to the Newton’s second law, the equations of horizontal motion for the conveyance in $x$-direction and $y$-direction can be represented as:

where $m$ represents the mass of conveyance, $x$ and $y$ represent the displacements of conveyance in $x\text{-direction}$ and $y\text{-direction}$ respectively,$F_x$ and $F_y$ represent the disturbing forces on conveyance in $x$-direction and $y$-direction respectively, and $k$ represents the lateral equivalent spring stiffness for conveyance. The lateral equivalent spring stiffness of rope-guided conveyance can be found in references [4, 7].

The equations of rotation for the conveyance about the vertical axis can be represented as:

where $J$ represents the mass moment of inertia of the conveyance about the vertical axis, $\theta$ represents the angular displacements of conveyance about vertical axis, $M_x$ represents total disturbing torque exerted on the conveyance about vertical axis, and $k_t$ represents the equivalent angular spring stiffness for conveyance about vertical axis. In some Chinese mine hoisting practices, the hoist rope attachment and the tail rope attachment are equipped with the thrust bearings, which can eliminate the torsion from hoist rope and tail rope, so the total disturbing torque only takes the aerodynamic moment on the conveyance about vertical axis into consideration.

Fig. 1Mathematical model of rope-guided hoisting system

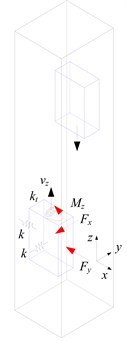
Fig. 2Shaft layout of mine cages

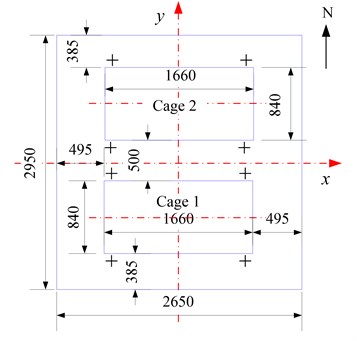
2.2. Shaft parameters

Fig. 2 gives shaft layout of mine cage, and the main parameters of shaft layouts are given in Table 1. The ventilation air speeds are 0, 2 m/s, 4 m/s, 6 m/s and 8 m/s respectively. The time-speed diagram in vertical direction of mine cage is shown in Fig. 3.

2.3. CFD modelling

The commercial code, ANSYS FLUENT 14.5, has been employed to simulate these cases with PISO scheme. In this study, the ventilation air flow is downcast, so the upper entrance is a velocity inlet boundary condition and the lower exit is pressure outlet boundary condition. All other boundary conditions are no slip at the wall. User-defined functions (UDFs) were written to define the vertical velocity of conveyances and to solve the equations of horizontal motion for conveyances with the Newmark-beta method $\text{(}\gamma =$ 1/2, $\beta =$ 1/4) [8]. The movements of conveyance have been implemented using a dynamic mesh with the local cell remeshing method in ANSYS FLUENT. As the local cell remeshing method only affects the tetrahedral cell types in the mesh [9], tetrahedral meshes were generated in the domain. Fig. 4 illustrates the Compute meshes and there are about 4×10⁵ control volumes. And the shear-stress transport (SST) $k-\omega$ model [10] was used for the turbulent air flow. These five transient cases were resolved using a characteristic time step of 0.002 seconds, and the total time is 16.6 seconds for the hoisting conveyances. There are 8300 time steps in total and 50 iterations for each maximum time step to resolve each case. About 20 h of CPU time in a 4-nodes HPC cluster were required to complete each numerical simulation.

Fig. 3Time-speed diagram in vertical direction

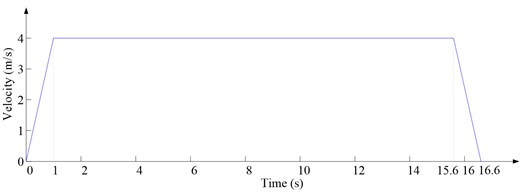
Fig. 4Compute meshes

3.1. Results

When two cages pass each other, pressure contours under different ventilation air speed are shown in Fig. 5. Here, $v_{in}$ denotes the ventilation air speed.

Fig. 5Pressure contours under different ventilation air speed

a)$v_{in}=$0 m/s

b)$v_{in}=$2 m/s

c)$v_{in}=\text{4}$ m/s

d)$v_{in}=$6 m/s

e)$v_{in}=$8 m/s

Fig. 6Simulation results for ascending cage 1 in north-south direction

a) Lateral aerodynamic force

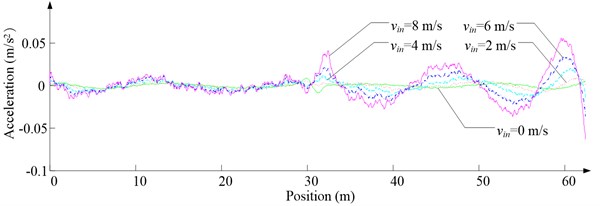
b) Lateral acceleration

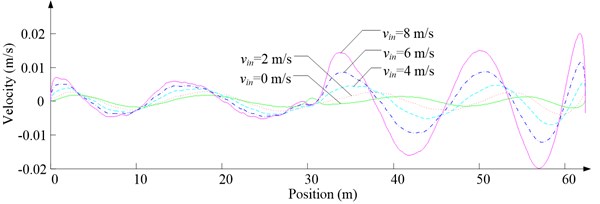
c) Lateral velocity

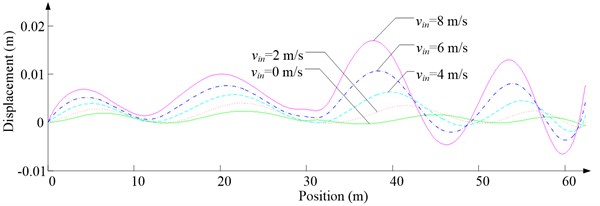
d) Lateral displacement

Fig. 6 shows the lateral aerodynamic force, lateral acceleration, velocity and displacement of ascending cage 1 in north-south direction, and Fig. 7 shows the lateral aerodynamic force, lateral acceleration, velocity and displacement of descending cage 2 in north-south direction. Fig. 8 shows the lateral aerodynamic force, lateral acceleration, velocity and displacement of ascending cage 1 in east-west direction, and Fig. 9 shows the lateral aerodynamic force, lateral acceleration, velocity and displacement of descending cage 2 in east-west direction. Here, $F_{cr}$ denotes the Coriolis force.

Fig. 7Simulation results for descending cage 2 in north-south direction

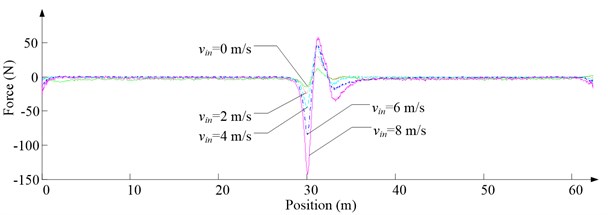
a) Lateral aerodynamic force

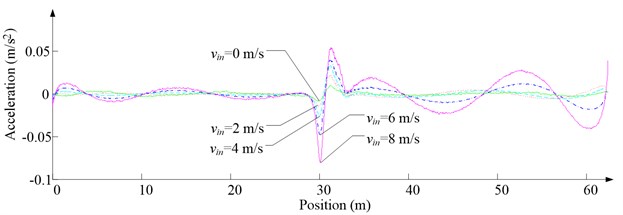
b) Lateral acceleration

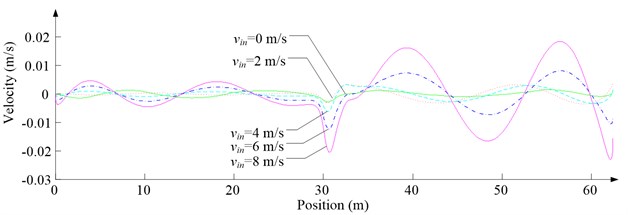
c) Lateral velocity

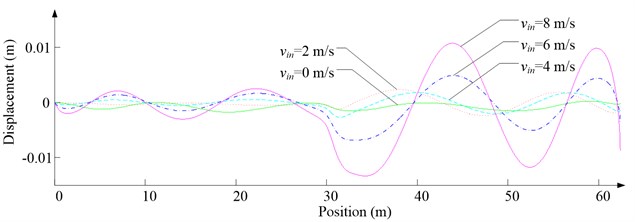
d) Lateral displacement

Fig. 8Simulation results for ascending cage 1 in east-west direction

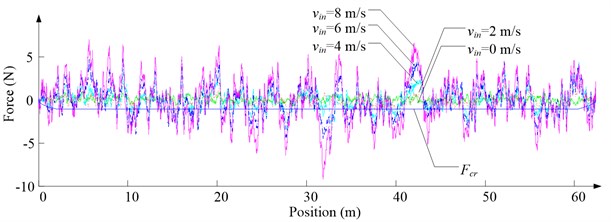
a) Side disturbing force

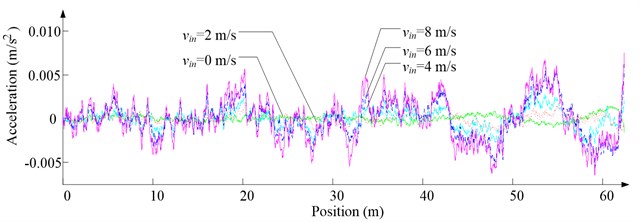
b) Side acceleration

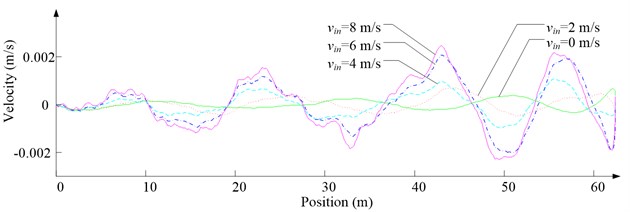
c) Side velocity

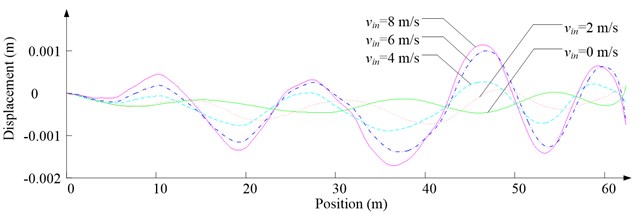
d) Side displacement

Fig. 9Simulation results for descending cage 2 in east-west direction

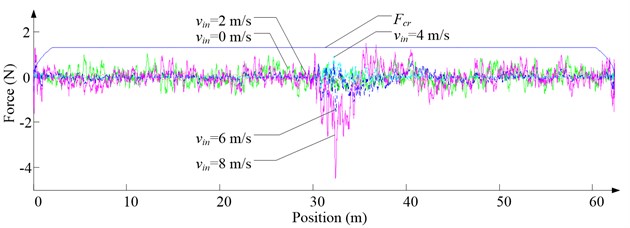
a) Side disturbing force

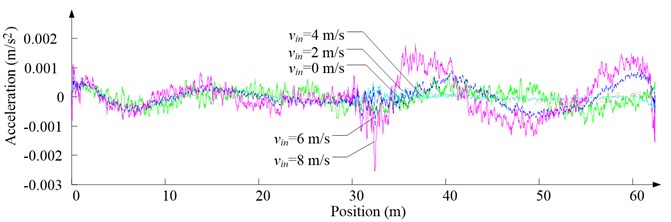
b) Side acceleration

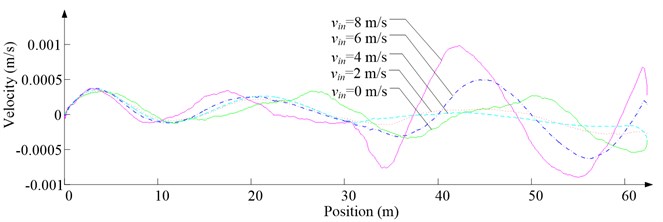
c) Side velocity

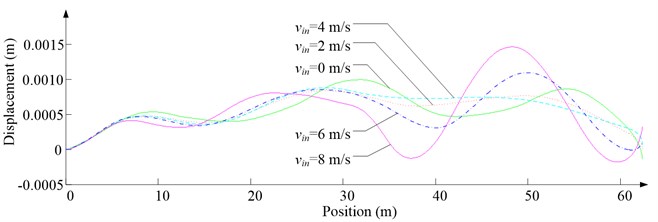
d) Side displacement

Fig. 10Simulation results for ascending cage 1 around z-axis

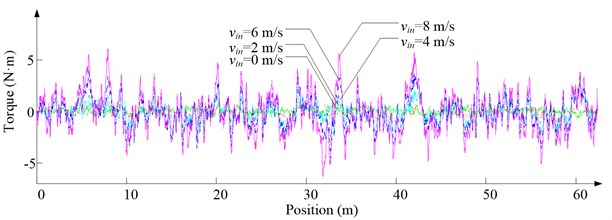
a) Aerodynamic torque

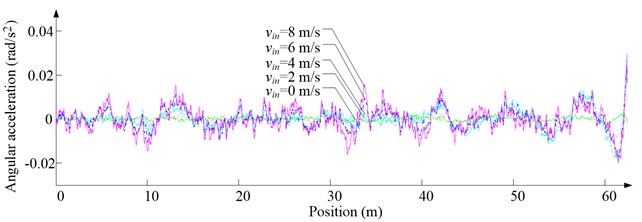
b) Angular acceleration

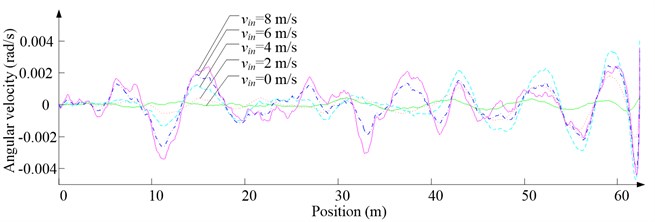
c) Angular velocity

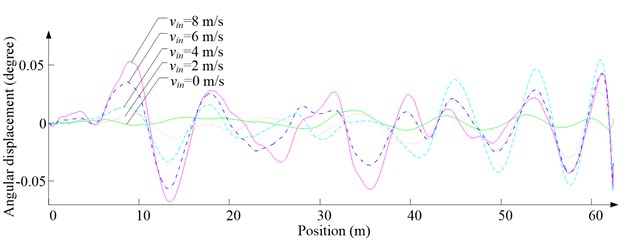
d) Angular displacement

Fig. 11Simulation results for descending cage 2 around z-axis

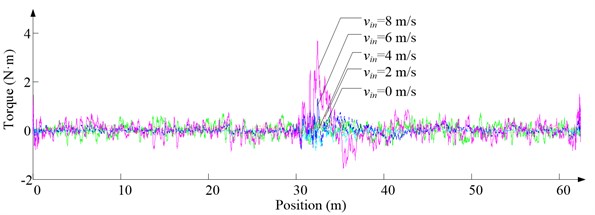
a) Aerodynamic torque

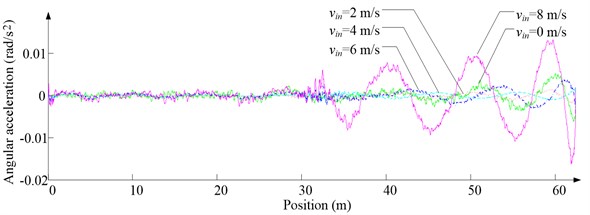
b) Angular acceleration

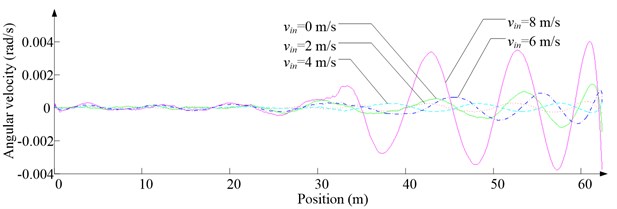
c) Angular velocity

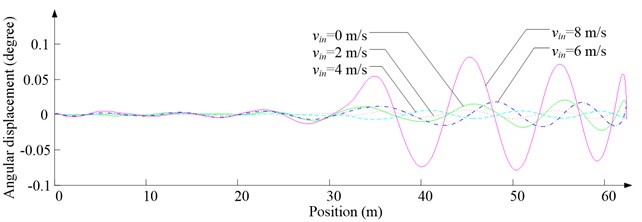
d) Angular displacement

3.2. Discussion

As Fig. 5 shows, the ventilation directly affects the pressure contours around the cages. As Fig. 6-9 show, the ventilation has a significant effect on horizontal displacement of conveyance, because the aerodynamic force is directly related to the ventilation air speed. As Fig. 10 and Fig. 11 show, the rotation of conveyance about vertical axis is very small, because the hoist rope attachment and the tail rope attachment equipped with the thrust bearings eliminate the torsion from hoist rope and tail rope.

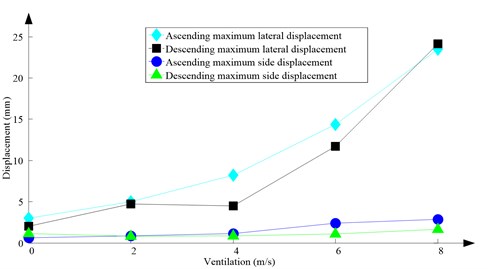
As Fig. 12 shows, with the increase of ventilation air speed, the maximum lateral and side displacements of ascending conveyances also increase, while those of descending conveyances do not always increase, because the ventilation air flows downcast. And the maximum lateral displacement is much larger than the maximum side displacement, because the lateral aerodynamic forces are much larger than the side aerodynamic forces.

Fig. 12Maximum horizontal displacement