Wave-based prediction analysis for dynamic-response problem in non-convex domain

2.1. Problem description

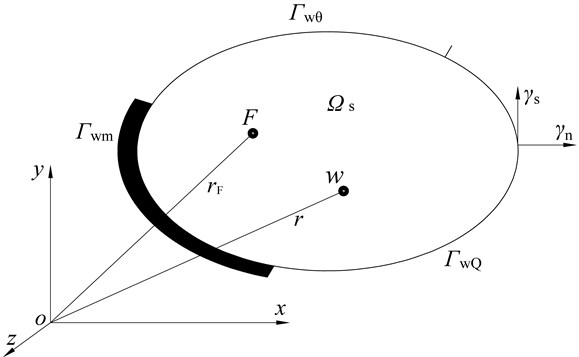
Basic principles of WBM for a general convex plate design domain are briefly discussed. As shown in the Cartesian coordinate system in Fig. 1, a thin-plate structure exists and is excited by a harmonic normal point force $F$ at position $r_F(x_F,y_F)$. In Fig. 1, ${\mathrm{\Omega }}_S$ is the structure design domain, and ${\mathrm{\Gamma }}_{w\theta }$, ${\mathrm{\Gamma }}_{wm}$ and ${\mathrm{\Gamma }}_{wQ}$ are the structure boundary conditions.

Fig. 1Convex plate domain

Two types of plate-bending theories exist, namely, Kirchhoff plate-bending theory and Reissner-Mindlin plate-bending theory. WBM as described in this research is based on the Kirchhoff plate-bending theory. In Kirchhoff theory, the rotational inertia and shear deformation effects are negligible. Considering the thin-plate structure problem, the Kirchhoff plate-bending theory could yields accurate results in low and mid frequency range. According to the Kirchhoff plate-bending theory, the time harmonic out-of-plane displacements function $w(x,y)$ in the problem domain ${\mathrm{\Omega }}_S$ is governed by the following fourth-order partial differential equation:

where ${\nabla }^4={\partial }^4/\partial x^4+2{\partial }^4/\partial x^2\partial y^2+{\partial }^4/\partial y^4$. $\delta$ is the 2-D Dirac-delta function. The bending wave number $k_b$ and the plate structure bending stiffness $D$ are defined as: $k_b=\sqrt[4]{\rho t{\omega }^2/D}$ and $D=E(1+i\eta )t^3/12(1-{\mu }^2)$, respectively. In Eq. (1), symbols $t$, $E$, $\mu$, $\omega$, $\eta$, and $\rho$ represent the plate thickness, material elasticity modulus, material Poisson’s ratio, circular frequency of bending wave, material loss factor, and plate material density, respectively. In addition, symbols $i$ is the unit imaginary number. Kirchhoff bending theory is tested to be correct when the bending wave length $\lambda$ is six times greater the plate thickness $t$.

In plate-structure dynamic-response analysis, Kirchhoff plate-bending theory is governed by a fourth-order equation differential equation that uniquely defines the displacement function $w(x,y)$. The boundary conditions are specified for each evaluated point in the plate-structure boundary. In addition, the boundary conditions of the considered plate domain ${\mathrm{\Omega }}_S$ has three parts (Fig. 1): 1) the kinematic boundary condition ${\mathrm{\Gamma }}_{w\theta }$ where the out-of-plane translational and the normal rotational displacements are imposed, 2) the mixed boundary conditions ${\mathrm{\Gamma }}_{wm}$ that impose the out-of-plane translational displacements and the normal bending moments, and 3) the mechanical boundary conditions ${\mathrm{\Gamma }}_{mQ}$ that impose the normal bending moments and the equivalent shear forces.

The differential operators for the out-of-plate displacement, then the rotational displacement, bending moment and generalized shear force are defined as:

where ${\gamma }_n$ and ${\gamma }_S$ are the two arc coordinates in the normal and tangential directions of the plate-structure boundary, respectively.

2.2. The field variable expansion

For WBM application to bounded problems, the convexity of the considered problem domain is a sufficient condition for the theoretical convergence of WBM. This application approximated the field variables as an expansion based from functions that exactly satisfy the governing dynamic equations. In addition, an approximation error is induced in the boundary and interface conditions. Integrally minimizing this approximation error leads to the solution of the system.

In the considered design domain, the time harmonic out-of-plane displacement function $w(x,y)$ is approximated by the following field variable expansion:

where each wave function ${\mathrm{\Psi }}_b(x,y)$ satisfies the homogeneous part of the dynamic function shown by:

where $(k_{b,x}^2+k_{b,y}^2{)}^2=k_b^4$ and $w_b$ represent the unknown participation factors of wave functions; ${\mathrm{\Psi }}_b(x,y)$, $k_{b,x}^{}$ and $k_{b,y}^{}$ represent the $x$ and $y$ component of the wave vector, respectively; and $n_b$ is the number of wave functions. Function ${\widehat{w}}_F(x,y)$ is a particular solution function to consider the inhomogeneous portion of the dynamic equation that arises from the external loading applied to the plate structure. In addition, the wave functions are restricted to the interval [−1, 1] in the application region to ensure that the amplitudes of the wave functions are less than 1.

The particular solution function ${\widehat{w}}_F(x,y)$ satisfies the inhomogeneous part of the dynamic Eq. (1) arising from the external loading. Only an excitation by normal point forces is considered in this study, and the particular solution function for a point force loading of an infinite plate is given as:

where $r_{sF}=\sqrt{(x-x_F{)}^2+(y-y_F{)}^2}$, $H_0^{\left(2\right)}$ is the zeroth-order Hankel function of the second kind. In Eq. (5), $H_0^{\left(2\right)}\left(x\right)=J_0\left(x\right)-i{Y}_0\left(x\right)$, $J_0\left(x\right)$ and $Y_0\left(x\right)$ are the Bessel functions of the first and second kind, respectively.

2.3. Weighted residual formulation

The field variable Eq. (3) fits exactly with the governing dynamic Eq. (1), irrespective of the unknown wave function contribution factors $w_{\mathrm{b}}$. These contribution factors are determined by minimizing the approximation errors of the boundary conditions and the continuity condition through the weighted residual formulation. The weighted residual formulation ${\widehat{w}}_F(x,y)$of the boundary conditions is defined as:

Substitution of the field variable expansion and the weighting function expansion into weighted residual formulation leads to a typical WBM system solution.

2.4. Wave function selection

In general, an infinite number of wave functions can satisfy the homogeneous differential dynamic Eq. (1). To apply WBM in numerical analysis, wave functions expansion must be truncated to a finite set. In WBM, the maximum wave number $k_b$, i.e., $k_b^{max}$, depends on the analysis frequency range and the dimensions of considered problem. Wave numbers $k_b$ ($k_{b,x}$ or $k_{b,y}$) are selected based on the outline dimensions ($L_x$×$L_y$) of a (preferably the smallest) rectangular circumscribing the plate domain ${\mathrm{\Omega }}_S$.

Among the first types of wave number, $k_{b,x}$ and $k_{b,y}$ are chosen such that an integer number of half wavelengths equals the length of the rectangular box in the corresponding direction. The other component of the wave number is calculated from the wave number $k_b$ of the considered frequency. Vanmaele [6] has proposed two sets of wave functions, shown in Eq. (7). The first set of wave functions is cosine function-related whereas the second set is sine function-related. The two types of wave function are written as:

Desmet [4] proved that the first group of wave functions is theoretically sufficient for the convergence of the WBM in the convex-considered domain. In this study, the cosine-associated wave functions are chosen, and wave numbers can be expressed as:

Among the plate structure domain, the number of bending wave functions $n_b$ that are included in the field variable expansion in Eq. (3), is related to the excited force frequency and the dimensions of the enclosing rectangular box: $n_b=4(n_{b1}+1)+4(n_{b2}+1)$.

However, finite wave functions can only be used in practical calculations. An infinite number of wave functions should satisfy the homogeneous differential equations. Therefore, the set of wave functions is truncated by applying a frequency-dependent truncation rule. The truncation rule is stated as:

where $T$ ($\ge$2) is the truncation coefficient; a truncation coefficient of $T=$ 10 is adopted in this study. The integer truncation value $n_{b1}$ and $n_{b2}$. $L_x$ and $L_{\mathrm{y}}$ are the length parameter and width parameter of the smallest rectangle around the outline domain, respectively. Through this formula, the largest wave number $k_b^{max}$ of the bending wave functions included in the plate structure is obtained within the considered frequency. As a result, the number of wave functions increases approximately linearly with excitation frequency.

3.1. Basic conception of multi-level modeling

A sufficient condition to ensure the convergence of WBM is that the design domain should be convexity domain. This is the main drawback of WBM. In response, the non-convex problem geometries must be decomposed into many convexity sub-domains. As a result, when the number of sub-domains increases, the integration length also increases. This further leads to an additional computational loading. On the other hand, some geometrical shapes, such as problem domain with circular and elliptic shapes, cannot be divided into convex sub-domains. To deal with this problem, two kinds of approaches aim to overcome these limitations were introduced recently. The first method involves use of multi-level modeling framework to alleviate the problems considered domain decomposition and geometrical requirement of structural problems with inclusions. The second approach is utilizing a hybrid FE-WBM formulation, i.e., FEM is applied in complex domain, whereas WBM is applied in convex domain. The multi-level modeling approach is also presented in this paper.

The theoretical basis for the multi-level conception is the superposition principle and the multiple-scattering theories. In the multi-level theory of WBM, the original problem can be decomposed into a single bounded sub-problem and one or more unbounded sub-problems (also termed levels). The bounded sub-problem boundary matched the boundary of original problem. In addition, the unbounded sub-problems boundary matches as well as the original problem boundary. Subsequently, the original problem is decomposed into the following levels with corresponding wave function sets, boundary residuals, and weighting functions. In the multi-level theory, the dynamic-response of various levels is superposed to form the dynamic response of the original problem.

Considering that the original problem converted bounded levels to unbounded levels, the former contains no holes or inclusions, and WBM tools become usable. In the multilevel modeling, the bounded levels ${\mathrm{\Omega }}_b$ describe the interior dynamic behavior of bounded sub-problems. Meanwhile, the unbounded levels ${\mathrm{\Omega }}_{ub}$ consider the scattering behavior of an inclusion in an infinite homogeneous medium to model one hole or inclusion in an infinite domain. Consequently, this technique facilitates obtaining efficient and flexible numerical tactics for analyzing the mid-frequency dynamics of complex geometrical domain.

To model these unbounded parts, new wave function sets are defined for unbounded plate problems. The solution function $w(x,y)$ is written as the superposition of several field variable expansions $w_b(x,y)$ and $w_{ub}(x,y)$, which need to satisfy the governing equation. The wave function $w_b(x,y)$ of bounded fields should fit the non-reflecting boundary conditions imposed at ${\mathrm{\Gamma }}_{\mathrm{\infty }}$. Meanwhile, the wave function $w_{ub}(x,y)$ of unbounded fields should satisfy the non-reflecting boundary conditions imposed at ${\mathrm{\Gamma }}_b$. Modeling each of the sub-problems using WBM and coupling them using the superposition principle help obtain the consequent response fields of the original problem.

A multilevel modeling approach is developed for unbounded acoustic multiple-scattering problems. The procedure for this approach involves four steps: 1) division of the original problem into various levels containing unbounded and bounded sub-domains; 2) selection of wave functions for each level containing a sub-domain design i.e., a wave function that can represent any arbitrary field on that boundary; 3) construction of the system of equations, and the weighted residual formulation; and 4) solution formulation and post-processing showing each point representing combined levels. Through this modeling technique, the dynamic-response problem of domain with concave boundary is investigated.

3.2. Basic conception of complement graph

The discussion on multi-level modeling in the previous section illustrates the feasibility and efficiency to cope with the 2-D domain problem through multiple circular holes or square holes [19]. However, some difficulties are encountered, such as the concave-domain problem.

To overcome these geometrical limitations in WBM, a complement-graph conception is proposed in this study. The multi-level modeling theory and superposition principle constitute the basic foundation of complement graph-conception. As shown in Fig. 2(a), a concave domain $\mathrm{\Omega }$ consists of two kinds of boundary characteristics i.e., convex curve ${\mathrm{\Gamma }}_1$, and concave curve ${\mathrm{\Gamma }}_2$. Considering the curve ${\mathrm{\Gamma }}_2$, the concave domain $\mathrm{\Omega }$ could not be divided into many kinds of convex sub-domains, and the traditional multi-level modeling could also not solve this problem. To deal with these concave-domain problem limitation, the addition a convex complement graph domain ${\mathrm{\Omega }}_C$ on to the concave boundary curve ${\mathrm{\Gamma }}_2$, as shown in Fig. 2(b), results in a new convex domain ${\mathrm{\Omega }}_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}=\mathrm{\Omega }\cup {\mathrm{\Omega }}_C$. In this study, the added convex-domain ${\mathrm{\Omega }}_C$ is named the complement graph.

As shown in the Fig. 2, the concave domain ${\mathrm{\Omega }}_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}$ has two convex boundaries, ${\mathrm{\Gamma }}_1\cup {\mathrm{\Gamma }}_3$. The concave domain ${\mathrm{\Omega }}_C$ also has two convex boundaries, ${\mathrm{\Gamma }}_2\cup {\mathrm{\Gamma }}_3$. Defining the convex domains of ${\mathrm{\Omega }}_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}$ and ${\mathrm{\Omega }}_C$ as levels renders multi-level modeling theory applicable. Apparently, the convex design domains ${\mathrm{\Omega }}_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}$ and ${\mathrm{\Omega }}_C$, are easy to deal with through WBM theory. In the next section, the feasibility and efficiency of complement-graph conception is illustrated through numerical verification studies where methodology is applied for Kirchhoff plate-bending problems.

Fig. 2Complement-graph conception

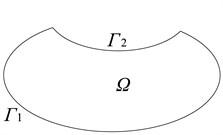
a)

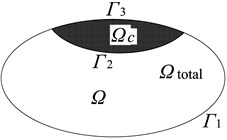
b)

3.3. An application of complement graph

The concave-domain problem is discussed in this section. Combination complement-graph conception and multi-level modeling theory are considered, and the application of the problem is shown in Fig. 3.

Fig. 3Complement graph method

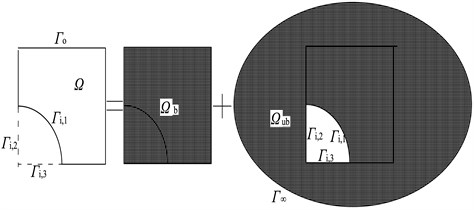
According to traditional WBM and multi-level modeling, accurately modeling this plate structure accurately (Fig. 3) is possible. Dividing the concave problem into convex sub-domains is also impossible. The quarter circle boundary ${\mathrm{\Gamma }}_{i,1}$ could be approximated by a large number of straight edges, but this step leads to a rough approximation and a large number of sub-domains. Consequently, the computational efficiency of WBM is jeopardized

Through the multi-level approach and complement-graph conception, the concave domain ${\mathrm{\Omega }}_S$ problem is decomposed into two levels: one bounded level and one unbounded level that are both coupled at the boundaries. The bounded levels ${\mathrm{\Omega }}_b^{}$ describe the interior dynamic response behavior of the bounded sub-problems with boundaries ${\mathrm{\Gamma }}_O\cup {\mathrm{\Gamma }}_{\mathrm{i},2}\cup {\mathrm{\Gamma }}_{i,3}$. The unbounded levels ${\mathrm{\Omega }}_{ub}^{}$ consider the scattering behavior of an inclusion in an infinite homogeneous medium, with inner boundaries ${\mathrm{\Gamma }}_{i,1}\cup {\mathrm{\Gamma }}_{i,2}\cup {\mathrm{\Gamma }}_{i,3}$. The solution field function $w(x,y)$ is written as the superposition of several fields, $w_b$ and $w_{ub}$, which is required to satisfy the governing Kirchhoff plate-bending equation. Furthermore, the unbounded fields should also satisfy non-reflecting boundary conditions imposed at ${\mathrm{\Gamma }}_{\mathrm{\infty }}$.

3.4. Wave functions of complement graph

After identifying the field variable expansions for the different levels, they combined with the common domain ${\mathrm{\Omega }}_S$ by using the superposition principle. In the bounded domain ${\mathrm{\Omega }}_b$, the bounded wave functions should be defined based on the indirect Trefftz principle that is shown by Eq. (4).

In a similar manner, the unbounded wave functions should be defined based on the indirect Trefftz principle; the wave function can be written as: $\left({\nabla }^2+k_b^2\right)\left({\nabla }^2-k_b^2\right)w_{ub}(x,y)=0$, where no external force is applied within the considered unbounded level.

To satisfy the Kirchhoff plate-bending theory, a sufficient condition is achieved when unbounded wave functions satisfy either $({\nabla }^2+k_b^2)w_{ub}(x,y)=0$ or $({\nabla }^2-k_b^2)w_{ub}(x,y)=0$ and the non-reflecting boundary conditions imposed at boundary ${\mathrm{\Gamma }}_{\mathrm{\infty }}$. Considering the purely outgoing nature of the sub-domain, extra caution is unnecessary. Furthermore, the sub-domian is implicitly represented in the wave function set [22].

After defining the wave function of the unbounded domain and bounded domain, the field variable expansions of bounded and unbounded levels are combined using the superposition principle. Consequently, the multi-level field variable expansion can be stated as:

where ${\sum }_{b=1}^{n_b}{w}_b{\mathrm{\Psi }}_b(x,y)+{\widehat{w}}_{bF}(x,y)$ is the solution of the bounded domain problem, and ${\sum }_{ub=1}^{n_{ub}}‍w_{ub}{\mathrm{\Psi }}_{ub}(x,y)$ is the solution of the unbounded domain problem. Consequently, the composite multi-level function set is defined, and the wave model can be constructed by enforcing the boundary conditions through the application of a weighted residual formulation. This formulation is analogous to the weighted residual formulation for bounded problems Eq. (6) introduced in Section 2, but residuals are now expressed in terms of the new, composite wave function set. Using the weighted residual formulation, the proposed multi-level displacement expansion and weighting function expansion leads to a linear system of algebraic equations. These equations could be solved to obtain the wave function contribution factors of the displacement of the considered problem domain $\mathrm{\Omega }$.

4.1. Model description

Taking for example a rectangle plate with one elliptic cut-out in the left-bottom corner, the calculation of the vibration by the WBM is carried out. Fig. 4 shows the geometry of the considered problem.

Fig. 4Rectangle plate

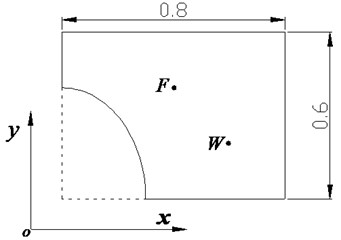
A rectangle plate containing one elliptic cut-out in the left-bottom corner is excited by a harmonic mechanical loading with prescribed under excitation frequency, amplitude, and direction. The boundary of the plate is simply supported. The semi-major axis and semi-minor axes of the ellipse are 0.4 m and 0.3 m, respectively. A unit point time-harmonic force with $z$ direction is applied at point $F$ (m, m), as shown in Fig. 4. Two evaluation points location point locations exist, i.e., $F$ (m, m) and $W$ (0.6 m, m).

For rectangle plate structure, the rectangular Cartesian coordinate system is used, with the coordinate origin set at the ellipse center. The length $L_x$ of plate is 0.8 m, the width $L_y$ is 0.6 m, and thickness is 0.001 m. The plate is steel based, and the mechanical properties of this steel are shown in Table 1.

4.2. Calculation and comparison

Fig. 4 shows the impossibility to divide the problem into convex sub-domains, and traditional WBM could not to deal with this problem. Through the complement-graph conception and the multi-level modeling theory, the multi-level WBM is introduced. In the numerical calculation, the variations of vibrations are with the frequency ranges 0-800 Hz, and the frequency step size is 2 Hz. to compare the computational efficiency of multi-level WBM and FEM in the low and mid frequency range, convergence analysis of structural dynamic response is performed.

In the dynamic-response analysis, the truncation coefficient $T$ is defined as 10 to illustrate that the multi-level extension of WBM accurately describes the dynamic response behavior. In addition, multi-level WB model contains only 250 basis functions in the displacement expansion (150 bounded and 100 unbounded wave functions). Furthermore, WBM is implemented in the MATLAB/R2007 environment.

Considering that the business software MSC.Patran/Nastran is a proven and widely used numerical tool for structural dynamic-response analysis, all FEM predictions are calculated using MSC/Nastran 2005. The finest 8-noded Nastran model is defined as a reference for convergence curves. To ensure high numerical precision, the model is fine meshed and consisted of 78 200 quadratic elements within the plate structure.

Fig. 5 shows a contour of the structural displacement at 500 Hz obtained using both MSC/Nastran 2005 and a multi-level WBM. Results show that multi-level WBM can accurately describe the spatial distribution of the dynamic displacement field by using complement-graph conception. Fig. 5 shows that using WBM can achieve accuracy similar to FEM but with less DOFs and fast convergence. In the other frequencies, the displacement contour plots are considerable correlate.

Fig. 5Comparison of predictions in the displacement response of WBM and FEM

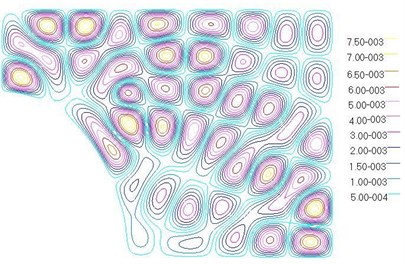
a) WBM, 250 DOFs

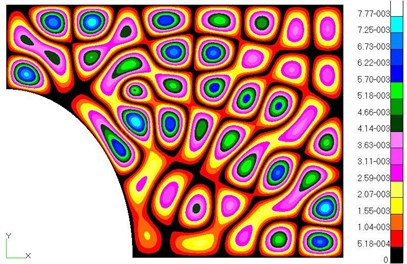
b) FEM, 196167 DOFs

Fig. 6 compares the predicted displacement response for evaluation point W within (0-800 Hz) frequency and the technique includes both FEM and multi-level WBM. Fig. 7 compares the predicted displacement response for evaluation point $F$ within (0-800 Hz) frequency and the technique also includes both FEM and multi-level WBM.

According to Figs. 6 and 7, multi-level WBM predictions considerable agree with conventional prediction techniques such as FEM throughout the entire frequency range of interest. Compared with FEM, WBM has less computational loading and more efficient convergence properties.

Fig. 6Displacement response at point W

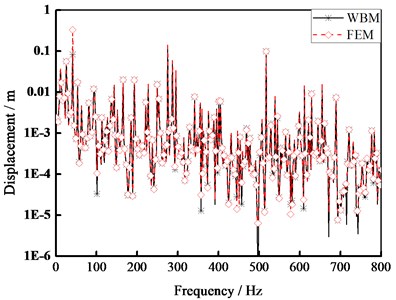
Fig. 7Displacement response at point F

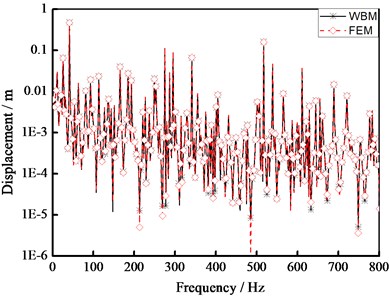
Comparison of data in Figs. 5-7 reveals that the numerical result of Patran/Nastran and WBM are similar, whereas WBM has less DOFs than that using MSC/Nastran soft code. Generally, these examples show that the multi-level WBM for plate-bending problems perform better than FEM within both low and mid frequency ranges.

Numerical results exhibit considerable improvement in terms of efficiency in concave problem by using the complement-graph conception and multi-level modeling theory. Numerical results show that the multi-level multi-level modeling theory of WBM can accurately describe the spatial distribution of the dynamic displacement field combination through complement-graph conception. Similar, displacement contour plots are considerably correlated within different frequency ranges.

4.3. Convergence analysis

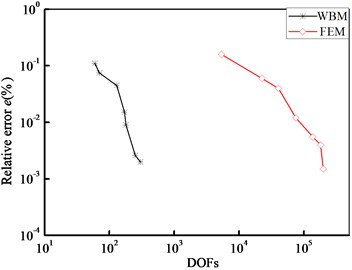
The accuracy of FEM analysis depends on the number of elements, selected shape functions. While, the accuracy of WBM analysis depends on the number of wave function. Fig. 8 plots the variation in relative errors and the degrees of freedom (DOFs) for the displacement prediction amplitudes of point $W$ (m, m) at 500 Hz frequency.

Fig. 8 shows that WBM has better convergence than element based methods. The high computational efficiency is likely to become even more definite.

Fig. 8Comparison of the convergence of FEM and WBM