Adaptive supervisory switching control system design for active noise suppression of duct-like application

1. Introduction

Nowadays noise cancellation becomes more and more important for industrial applications [1-6]. Traditional passive noise cancellation techniques using sound absorbent materials can only suppress high-frequency acoustic noises effectively, usually higher than 500 Hz [7]. And, they are ineffective or tend to bulky for low frequency cases. In contrast with the passive noise suppression methods, active noise control techniques have excellent low frequency characteristic, with potential benefits in size, weight and cost [8].

While the characteristics of noise source and acoustic environment are time varying, tracking these changes and uncertainties is required for an active noise control system. To solve the changes and uncertainties tracking problems, various algorithms have been proposed. The most famous one is Filtered-x Least Mean Squares (FxLMS) algorithm proposed by different researchers independently. Several theoretical developments and successful applications are documented in the related literature [3, 9-12]. In particular, the secondary path between the loudspeakers and error sensors would be time varying as the temperature and noise propagation condition would vary even the noise source does not change. So in most actual applications, simultaneous secondary path identification is required. To solve secondary path identification problem, many adaptive online identification methods are reported [13-16]. But most of them could not be applied to the cases while secondary path varies rapidly, and not suited for multiple input multiple output applications with too many unknown parameters. And in many applications, secondary path is almost impossible, so in these situations, model-free algorithm is more attractive. Unfalsified control proposed by M. G. Safonov [17] using multiple controllers seems to be a good choice. But it can not apply for active noise control directly.

To solve the above problems, a new adaptive supervisory switching control is proposed. Section 2 introduces active noise control system modeling for duct-like applications. Section 3 introduces the proposed adaptive supervisory switching control method. Section 4 gives the real time active noise control test results. Section 5 comes to the conclusion.

2. Active noise control system modelling for duct-like applications

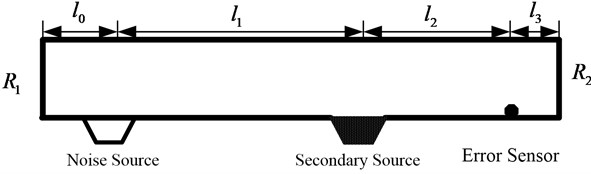
Schematic diagram of active noise control system for a duct-like application can be shown in Fig. 1. The soundincident from the left noise source is picked up by the microphone and after some processing by the active noise controller, this signal is fed to the secondary sources (loudspeaker) such that to the right side the primary signal and the additional signal cancel each other. The noise source is located at $l_0$ from one end of the duct, and an error sensor is located at $l_3$ from the other end of the duct. The secondary source is located at $l_1$ form the noise source. The pressure reflection coefficients in two ends are $R_1$ and $R_2$ respectively. The primary between the noise source and the secondary source is $P$, the secondary path between the secondary source and error sensor is $S$.

Fig. 1Schematic diagram for a duct-like application

According the steady state travelling wave theory, the frequency response for secondary path and the primary path can be obtained as follows:

where $H_p$ is the electroacoustic transfer function of the noise source, $H_s$ is the electroacoustic transfer function of the secondary source, $H_e$ is the electroacoustic transfer function of the secondary source. $D_p$, $D_p$ are the directivity factors. For $z$-transform:

where, $n_i$ is the integer near to $l_i{f}_s/c$, here $f_s$ is sampling frequency, $c$ is the sound speed. $N=2(n_0+n_1+n_2+n_3)$, while the sound speed changes with time, the whole system becomes time varying.

Unfold the above Eqs. (3) and (4):

3. Proposed adaptive supervisory switching control

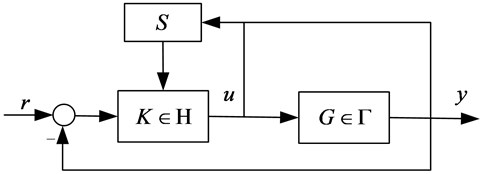
Over the last two decades, a lot of researches has put forward for a new adaptive theory, adaptive switching supervisory control. A typical adaptive switching supervisory control strategy is shown in Fig. 2. $S$ is data driven supervisor. The controlled plant $G$ belongs to a given model set ${\rm T}$. The controller $K$ belongs to a given controller set $H$. The current controller is chosen by a switching strategy.

Fig. 2Adaptive supervisory switching control

Considering the following closed loop control system:

where $G\left(s\right)$ is the transfer function of the controlled plant, and $K\left(s\right)$ is the transfer function of the controller, and $r$ is the reference signal, and $u$ is the control variable, $y$ is the output of the system.

Assuming $G$ belongs to set $H$, and $K$ belongs to a LTI controller family $\mathrm{\Gamma }$.

For a given signal $x\left(t\right)$ and:

is a trunction of $x\left(t\right)$, and the truncated norm is ${‖x‖}_{\tau }=\sqrt{\left({\int }_0^{\tau }{x}^2\left(t\right)dt\right)}$. While there exists $\alpha$, $\beta \ge 0$ for ${‖y‖}_{\tau }\le \alpha {‖r‖}_{\tau }+\beta$, the stability of the dynamic controlled system. Otherwise while:

the stability of the system is falsified. The performance index $J\left(K,u,y,\tau \right)$ is a positive function. It is defined according to the design specifications of $K$. The following index $J\left(K,u,y,\tau \right)$ is employed as the performance index in the control process:

where $\mathrm{*}$ denotes convolution, $w_1\left(t\right)$ and $w_2\left(t\right)$ is the solution of the following mixed sensitivity problem:

where $S$ is the sensitivity function. The block diagram of the proposed adaptive switching supervisory control is shown in Fig. 3.

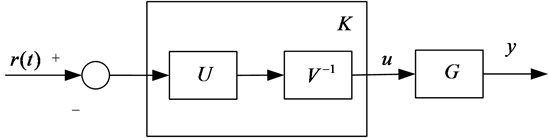
The closed loop system with $K=V^{-1}U$ can be illustrated in Fig. 4.

To choose the proper controller, the following falsification algorithm is employed as shown in Fig. 5.

Fig. 3Block diagram of the adaptive switching supervisory control scheme

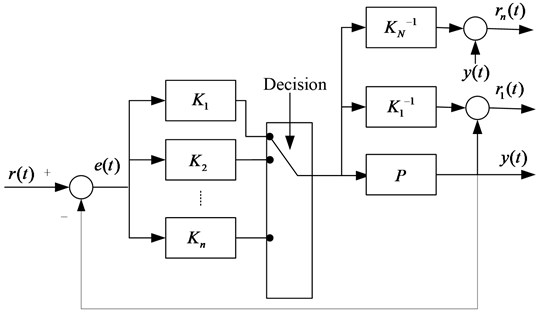
Fig. 4Closed loop control system with K=V-1U

Using mixed-sensitivity design method $K_i\left(s\right)=V^{-1}\left(s\right)U\left(s\right)\text{.}$ Then the following parameterization can be obtained:

Taking $U_{\lambda }={\lambda }_1{U}_1+\sum _{i=2}^n{\lambda }_1{V}_1{V}_i^{-1}{U}_i$:

By using $(u,y)$ in $\left[0,\tau \right]$, optimal $K_{\lambda \mathrm{*}}\left(s\right)$ can be obtained.

Fig. 5Falsification algorithm

4. Real time experimental tests and results

To test the proposed adaptive supervisory switching control algorithm, a test experimental platform is constructed using a 10 meters duct with two loudspeakers, two microphones and an acoustic rate sensor. One loudspeaker is used to generate noise while the canceling noise channeled through the other speaker. A microphone is placed in cancellation zone to pick up the resultant noise signal. The experimental platform schematic diagram is shown in Fig. 6. The duct parameters are shown in Table 1. To accelerate the experiment, rather than waiting for condition change, an air-conditioner is employed.

Fig. 6Experimental platform setup

To test the effectiveness of the proposed algorithm, FULMS with online identification algorithm is employed as the compared control algorithm. While the air-conditioner changes slowly, the control performance is shown in Fig. 7. It is clearly that the control performance of FULMS algorithm with online identification is still acceptable. While the air conditioner changes fast, the control performance can be shown in Fig. 8. The FULMS with online identification can not assure the satisfactory control performance any more.

Fig. 7Control performance with slow change of FULMS with online identification

But the proposed algorithm could gurateen a satisfactory suppression performance no matter how the air-conditioner changes, as shown in Fig. 9.

To show the effectiveness of the proposed adaptive switching supervisoy control algorithm, a white noise is chosen as the noise source. The control performance is shown in Fig. 10. The noise is suppressed to a great extent.

Fig. 8Control performance with fast change of FULMS with online identification

Fig. 9Control performance of the proposed adaptive switching supervisory control

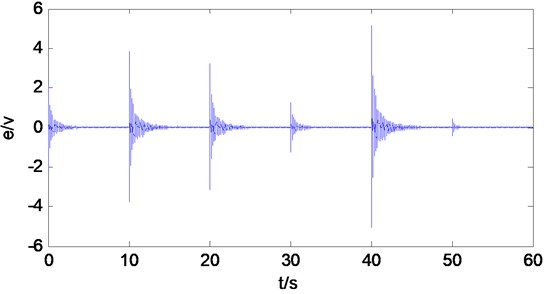
Fig. 10Control performance of the proposed adaptive switching supervisory control for white noise

5. Conclusion

An adaptive switching supervisory control algorithm is proposed with a new controller switching strategy in this paper for active noise suppression of duct-like application. Real time experiments were done. The experimental results show that the proposed algorithm has good noise suppression performance.