Conversion of inhomogeneous robin boundary conditions into virtual sources for wave motions and heat conduction

1. Introduction

Vibration engineering encounter a great quantity of longitudinal waves, transverse waves and heat conduction, such as parabolic or hyperbolic heat-conduction dynamics, acoustic or thermoacoustic oscillations, structural vibrations, quantum mechanics, electromagnetic waves, and so on. Any of these dynamics is governed by a Laplacian operator or its higher orders in space, which is often spatially non-uniform. As the boundary condition, Dirichlet, von-Neumann, or Robin, thereof is homogeneous, its eigenfunctions constitute an admissible, real, orthogonal and complete basis in the Hilbert space of a bounded region. This basis provides modal decomposition of the dynamics for system identification, computational intelligence, model reduction, real-time processing and design purposes. However, boundary conditions are inhomogeneous in many occasions; for instance, the differential equation of heat conduction is always accompanied by inhomogeneous boundary conditions, since temperature is non-zero in nature. With boundary inhomogeneity, the dynamics is essentially nonlinear, which prevents Hilbert space from being directly introduced for modal decomposition.

To remedy such a situation in this paper, we realize the inhomogeneous boundary conditions as virtual sources in conjunction with homogeneous boundary conditions. In one-dimensional cases, such a source is found to be a Dirac Delta distribution combined by its spatial derivatives on boundary. Therein, with the Laplace-Galerkin transform [1-3], both equations governing the interior and the boundary are integrated into a single 2D transfer-function of two independent variables: one is from the time and the other is from the space. Performing the inverse Laplace-Galerkin transform of the 2D transfer-function realizes back the dynamics into homogeneous boundary conditions with virtual sources, both of which yield the identical solution in the interior. With the homogeneous boundary resulting from the virtual-source realization, the Sturm-Liouville properties in Hilbert space are thus applicable for further analysis and synthesis in the mode-frequency domain.

The conversion of boundary inhomogeneity into virtual source has ever been conceptually applied to identify thermal inertia by inputting von-Neumann source [2], and to derive the mechanical energy of thermoacoustics [3]. In these decades, von-Neumann boundary source was employed to obtain order-reduced modelling of combustion instabilities in rocket motors. With these hints on application, this paper systematically extends to Robin sources and studies boundary topology. Robin inhomogeneity is fascinating and necessary for real practice, since the Dirichlet or von-Neumann boundary can be considered as a degenerated version of Robin boundary [4-7]. Therein, the boundary is the complement of the union of the exterior and the interior of the domain under consideration, so boundary conditions rely on the interaction between the process and the environment. Although degenerative Robin simplifies numerical or experimental investigation, the actual Robin boundary should be identified in practice through measured data, as seen in [8-13] for examples. Therein, Robin boundaries are identified for the study of cancer destruction during hyperthermia treatment, of the optical path length in inhomogeneous tissue, and of axisymmetrical induction in heating processes, respectively. To be sure, the conversion of Robin inhomogeneity into virtual source can make these important kinds of identification more accurate and reliable, since the virtual-source conceptually suggests installing an active source in measurement to trig out desired data.

Conversion of boundary inhomogeneity into virtual source also helps computational intelligence, since boundary inhomogeneity is conventionally treated as “conditions” that constrain the spatial-temporal evolution. The legitimate spatial-temporal solutions, including the integral solutions [14-15], finite-element approximation [16-17], and series solutions [18-20], have to be developed toward matching the boundary conditions. In vibration engineering, modal solutions are particularly popular, since it reveals the spatiotemporal structure and results in model reduction in practice. In cases of time-invariant environments, the response is usually computed by shifting the origin of spatial coordinate to the steady-state response, upon which the dynamics with homogeneous boundary condition can be solved by separation-of-variable method, as in [21] for example. This method can also be extended to time-varying environments by stepwise sampling the temporal continuity, as in [22-23] for examples. Compared with the virtual-source solution, this solution is numerical tedious and incapability of capturing sudden changes in the environment.

More importantly, virtual-source conversion lead to an input-output modelling that makes possible real-time signal processing. The differential equation in conjunction with the boundary inhomogeneity can give designers computer-time solutions by taking the boundary inhomogeneity as constraining conditions, but it is unable to catch the real-time nature. That is, such a computer-time version is offline plugged into computer simulation or calculation to merely obtain the solution as a function of a preset time-span. However, a real-time version is an emulator of natural evolution, wherein the state at the next instant is only dependent on the state and the boundary inhomogeneity at the present instant. It is unnecessary to know the history of the state and the boundary inhomogeneity to predict the future, since Nature has no memory. Galerkin projection of the converted dynamics with virtual source and homogeneous boundary onto a proper basis, such as those from Proper Orthogonal Decomposition (POD) [24-28], generates an order-reduced state-space realization. Given a freely assigned sampling time, Euler discretization of the state-space realization becomes the real-time version, which interprets the dynamic nature into two times of matrix multiplication and one time of matrix addition within a sampling time.

Compared with “conditions” realization of boundary inhomogeneity, virtual-source realization provides the following merits in practice:

1) It transforms the interaction between two distributed dynamics adjacent to each other into feedback interconnection, such as thermal-acoustic interaction in the fields of thermoacoustic engines [29] and combustion instabilities [30]. The construction of feedback makes possible the application of modern or classical control theory to help design and analysis.

2) Modal decomposition is applicable for computational intelligence and order-reduced modelling. It results in real-time version of distributed dynamics with inhomogeneous in digital signal processing (DSP), which can be directly programmed into a microcontroller for real-time estimation of state distribution and environmental changes, toward a newly sensing technology.

3) The real-time fashion above can still replace computer-time versions as a numerical simulator programmed into a generous computer. For a long run, it can be employed for efficient management of computer memory.

4) Virtual-source realization makes possible the frequency-domain identification of boundary inhomogeneity.

5) As the control actuation is set on some boundary, the virtual-source realization generates an input-output model served for feedback synthesis of boundary control systems.

6) Even with temporally discontinuous or impulsive environments, exact solutions can be calculated offline with virtual-source realization.

7) Active sources on boundary can be installed for identification of Robin coefficients.

2. The considered class of dynamics

This paper considers the following three types of distributed dynamics with inhomogeneous Robin boundary conditions:

and:

and:

Therein the spatial functions $\rho$, $k$ are real and positive in the bounded region $\mathrm{\Omega }\subset {\mathfrak{R}}^3$ is a bounded region, wherein the distributed output is denoted by $\psi$; on the boundary $\partial \mathrm{\Omega }$, $(\alpha ,\beta )\ne \left(0.0\right)$, $({\alpha }_1,{\beta }_1)\ne \left(0.0\right)$, $({\alpha }_2,{\beta }_2)\ne \left(0.0\right)$, and the boundary inhomogeneity is denoted by $f$ or $f_j$’s.

A kind of these three dynamics involves a spatial Laplacian operator $\mathcal{a}$:

or:

With the inner-product metric:

the Laplacian operators $\mathcal{a}$ in Eq. (4) and Eq. (5) belong to the Sturm-Liouville class $\mathcal{a}\in SL\left(\mathrm{\Omega }\right)$, that is, their eigenfunctions constitute a real, orthonormal, and complete basis of $L_2\left(\mathrm{\Omega }\right)$. A Sturm-Liouville operator is usually distinguished from its self-adjointness and the compactness of its inverse. With the Green’s second identity, it is easy to know that the elastic stiffness in Eq. (4) is a Sturm-Liouville operator [31]. As for the bending stiffness in Eq. (5), the following shows that it is belonging to Sturm-Liouville class.

Let two operators $\mathcal{P}$ and $\mathcal{Q}$ be defined by $\mathcal{P}={\rho }^{-1}{\nabla }^2$ and $\mathcal{Q}=k{\nabla }^2$, then the bending stiffness $\mathcal{a}$ becomes their composite, i.e. $\mathcal{a}=\mathcal{P}\mathcal{Q}$. For any $\psi$, $\varphi \in D\left(\mathcal{a}\right)$:

since ${\alpha }_1\left(\mathcal{Q}\psi \right)+{\beta }_1\nabla \left(\mathcal{Q}\psi \right)·\widehat{n}=0$ and ${\alpha }_1\varphi +{\beta }_1\nabla \varphi ·\widehat{n}=0$. Moreover:

since ${\alpha }_2\left(\mathcal{Q}\varphi \right)+{\beta }_2\nabla \left(\mathcal{Q}\varphi \right)·\widehat{n}=0$; ${\alpha }_2\psi +{\beta }_2\nabla \psi ·\widehat{n}=0$. Observe that:

since both sides equal ${\int }_{\mathrm{\Omega }}k{\nabla }^2\psi {·\nabla }^2\varphi dV$. Therefore, the bending stiffness operator $\mathcal{a}$ is self-adjoint. Moreover, the inverse of $\mathcal{a}$ is a compact operator in $L_2\left(\mathrm{\Omega }\right)$, since $\mathcal{a}$ is fourth-order differential operator. Therefore, its eigenfunctions constitute a real, orthonormal, and complete basis of $L_2\left(\mathrm{\Omega }\right)$. Moreover, it can be shown that both elastic stiffness and bending stiffness are positive definite in this work.

3. Laplace-Galerkin transform- a functional tool

With respect to the eigenfunctions set ${\left\{{\varphi }_{\lambda }\right\}}_{\lambda \in \mathrm{\Lambda }}$ of a Sturm-Liouville operator $\mathcal{a}$, the Galerkin transform $\mathcal{G}$ from spatial functions to modal functions, $F\left(\lambda \right)=\mathcal{G}\left[f\right(x\left)\right]$, is defined by:

Completeness and orthonormality of ${\left\{{\varphi }_{\lambda }\right\}}_{\lambda \in \mathrm{\Lambda }}$ of countable cardinality jointly imply that the Galerkin transform $\mathcal{G}$ has a unique inverse ${\mathcal{G}}^{-1}$, $f\left(x\right)={\mathcal{G}}^{-1}\left[F\right(\lambda \left)\right]$:

Then, the Laplace-Galerkin transform $\mathcal{H}$ from spatial-temporal functions to modal-complex functions is defined by the composite of the Galerkin transform $\mathcal{G}$ and the Laplace transform $\mathcal{L}$:

explicitly:

Accordingly, the inverse of Laplace-Galerkin transform ${\mathcal{H}}^{-1}$ is the composite of the inverse of Laplace transform and that of Galerkin transform, that is:

explicitly:

Here the domain $\mathrm{\Gamma }$ is an infinite line parallel to the imaginary axis, whereon the integral in Eq. (13) is converged.

Denote the temporal derivative $\partial /\partial t$ by ${\mathcal{D}}_t$, and let $\mathcal{a}$ be a Sturm-Liouville operator, $\mathcal{a}\in SL\left(\mathrm{\Omega }\right)$. For the set of spatial-temporal functions with homogeneous boundary and initial, the Laplace-Galerkin transform $\mathcal{H}$ is of:

where $h$ is a ratio of two expressions of finite or some infinite length constructed from two independent variables, one standing for space and the other for time, allowing for the operations of addition, subtraction, multiplication, integer exponents in time, and fraction-order exponents in space. For example:

The Laplace-Galerkin transform and its inverse perform transformation between Sturm-Liouville dynamics in space-time domain and 2D transfer-function in mode-frequency domain [1-3]. As an example to explain 2D transfer-function, let us find the impulse response of the following longitudinal wave $\widehat{G}$:

The elastic stiffness$-{\partial }^2/\partial x^2$ is of eigenvalues $\mathrm{\Lambda }=\left\{\text{1,}\text{4,}\text{9,}\text{…}\right\}$ associated with eigenfunctions ${\varphi }_{\lambda }\left(x\right)=\sqrt{2/\pi }\mathrm{s}\mathrm{i}\mathrm{n}\sqrt{\lambda }x$. Taking the Laplace-Galerkin transform on both sides of the differential equation with homogeneous boundary and initial yields:

that is, the 2D transfer-function of the dynamics $\widehat{G}$ is:

Correspondingly, the impulse response $g={\mathcal{H}}^{-1}G$ is to be:

To check whether this solution is correct, let us give the dynamics $\widehat{G}$ the 2D unit-pulse $u(x,t)=\delta \left(t\right){\sum }_{\lambda \in \mathrm{\Lambda }}{\varphi }_{\lambda }\left(x\right)$, where $\mathcal{H}u=1$. Integration of the differential equation from $t=0^{-}$ to $t=0^{+}$ yields the initial condition: $\psi (x,0)=0$ and $\dot{\psi }(x,0)={\sum }_{\lambda \in \mathrm{\Lambda }}^{}{\varphi }_{\lambda }\left(x\right)$. Thereby, the impulse response $g$ is just the solution of the initial-value problem:

which has the form solvable by the conventional separation-of-variable method. It can be found that two solutions are identical.

4. Virtual conversion of conditions into sources on boundary

This section demonstrates how to converts the boundary inhomogeneity into virtual source in conjunction with homogeneous boundary. This conversion is analogous to the strategy of Laplace transform dealing with non-zero initial conditions, wherein the initial inhomogeneity is realized as a virtual source comprising Dirac Delta function and its derivatives. Consider the following explanatory example- a normalized one-dimensional wave dynamics with initial inhomogeneity:

Taking the Laplace transform on Eq. (23a) with the help of integration by parts yields:

Then taking the inverse Laplace transform on Eq. (24) yields:

where $\delta$ is the Dirac delta distribution. The solution to Eq. (25) is almost the same as the solution to Eq. (23); both solutions are identical in the interior $t>0$ that is an open set, but different on the boundary $t=0$ that is a closed set.

Now consider the longitudinal wave dynamics $\widehat{G}$ in Eq. (1), which involves the elastic stiffness $\mathcal{a}$ in Eq. (4). As shown in Section 2, the elastic stiffness $\mathcal{a}$ is a Sturm-Liouville operator $\mathcal{a}\in SL\left(\mathrm{\Omega }\right)$ under the inner-product of Eq. (6). Let $\mathrm{\Phi }={\left\{{\varphi }_{\lambda }\right\}}_{\lambda \in \mathrm{\Lambda }}$ denote the eigenfunctions set of $\mathcal{a}$ corresponding to the eigenvalues set $\mathrm{\Lambda }\text{.}$ On the boundary $\partial \mathrm{\Omega }\text{,}$ firstly, substitution $\alpha {\varphi }_{\lambda }^{}+\beta \nabla {\varphi }_{\lambda }^{}·\widehat{n}=0$ for Eqs. (1b)$\times (-{\varphi }_{\lambda }^{})$ yields:

Secondly, substitution $\alpha \varphi +\beta \nabla {\varphi }_{\lambda }\bullet \widehat{n}=0$ for Eq. (1b)$\times \nabla {\varphi }_{\lambda }^{}·\widehat{n}$ yields:

In general, the sum of Eq. (26)$\times \beta /(\alpha +\beta )$ and Eq. (27)$\times \alpha /(\alpha +\beta )$ is to be:

Moreover, based on the Green’s second identity:

With Eqs. (26)-(29), performing Laplace-Galerkin transform $\mathcal{H}$on Eq. (1a) with inhomogeneous boundary conditions in Eq. (1b) yields:

where $\mathrm{\Psi }\left(\lambda ,s\right)\equiv \mathcal{H}\left[\psi \right(x,t\left)\right]$$\widehat{f}(x,s)\equiv \mathcal{L}\left[f\right(x,t\left)\right]$, and $B_{\lambda }$ is to be:

Therefore, in the sense of virtual source, the 2D transfer-function $G$ of the dynamics $\widehat{G}$ in Eq. (1) is:

With the 2D transfer-function of Eq. (32), the exact solution of Eq. (1) can be obtained even when the boundary inhomogeneity $f$ in Eq. (30) or Eq. (1b) is temporally impulsive or discontinuous.

Performing the inverse Laplace-Galerkin transform ${\mathcal{H}}^{-1}$ on the Eq. (32) yields:

where $q(x,t)\equiv {\mathcal{H}}^{-1}\left[Q\right(\mathrm{\lambda },s\left)\right]$. In Eq. (33), the boundary inhomogeneity $f$ in Eq. (1b) has been realized as the virtual source $q$ in Eq. (33a) in conjunction with homogeneous boundary of Eq. (33b). In the interior of the domain $\mathrm{\Omega }$, the response governed by Eq. (1) is identical to that governed by Eq. (33), since both have the same 2D transfer-function.

Next, consider the transverse wave dynamics $\widehat{G}$ in Eq. (2). For simple explanation, let us take its on-dimensional version:

This dynamics involves the bending stiffness $\mathcal{a}$ in Eq. (5):

which is a Sturm-Liouville operator, $\mathcal{a}\in SL\left(\right[0,\mathcal{l}\left]\right)$, under the inner-product of Eq. (6). Denote its eigenvalues set by $\mathrm{\Lambda }$ and eigenfunctions set by $\mathrm{\Phi }={\left\{{\varphi }_{\lambda }\right\}}_{\lambda \in \mathrm{\Lambda }}$.

With integration by parts (one-dimensional Green’s second identity), we have:

With Eq. (34b) and Eq. (35b), Eq. (36) can be rephrased to be:

With Eq. (37), performing the Laplace-Galerkin transform $\mathcal{H}$ on Eq. (34a) yields:

Then, performing the inverse Laplace-Galerkin transform ${\mathcal{H}}^{-1}$ on Eq. (38) yields:

The dynamics in Eq. (34) has been converted into the dynamics in Eq. (39), wherein the virtual source in Eq. (39a) comprises a Delta function $\delta$ and the second derivative of Delta function ${\delta }^{\text{'}\text{'}}\left(⟨\varphi ,{\delta }^{\text{'}\text{'}}⟩={\varphi }^{\text{'}\text{'}}\left(0\right)\right)$ distributed at $x=0$ in conjunction with homogeneous boundary in Eqs. (39b) and (39c). Both dynamics are identical in $(0,\mathcal{l}]$, since they have the identical 2D transfer-function.

As for the virtual-source realization of the dynamics of heat conduction in Eq. (3), it is similar to that of the dynamics of longitudinal wave as shown above. The above shows how the wave and heat-conduction dynamics with inhomogeneous boundary “conditions” can be almost converted to delta sources on boundary in conjunction with homogeneous boundary. Input-output modelling results therefrom and modal decomposition in Hilbert space becomes possible.

5. Investigation on boundary topology

In this section, the virtual-source solution and the separation-of-variable solution of a normalized, one-dimensional heat condition with one-side Dirichlet inhomogeneity are computed and then visualized in figures. It is expected to visualize between them the identical parts in the interior but the topological difference on the inhomogeneous boundary. Accordingly, consider the following parabolic dynamics:

Two cases of environments are considered: one is time-invariant in which $f\left(t\right)=1$ (Case I), and the other is time-varying in which $f\left(t\right)=\mathrm{s}\mathrm{i}\mathrm{n}\omega t$ (Case II).

The virtual-source conversion, as shown in Section 4, is employed to solve the Case I and Case II. Based on the Green’s second identity:

With Eqs. (40b) and (40c), taking the Laplace-Galerkin transform on Eq. (40a) yields:

As $f\left(t\right)=\text{1}$ in Case I, $F\left(s\right)=\text{1}/s$. Then taking the inverse Laplace-Galerkin transform on Eq. (42) yields:

In case II, let $f\left(t\right)$ be $\mathrm{s}\mathrm{i}\mathrm{n}\omega t$, that is, $F\left(s\right)=\omega /(s^2+{\omega }^2)$. Taking the Laplace-Galerkin transform again on Eq. (40a) yields:

The separation-of-variable method is improper to solve the solution of Case II, wherein the environmental temperature is time-varying. In Case I, the separation-of-variable solution is to be:

Fig. 1 shows the order-reduced solutions of Case I with 500 modes being considered. At $t=\text{0.5}$ the separation-of-variable solution in Eq. (45) is in juxtaposition with the virtual-source solution of Eq. (43) for comparison. It is found that both solutions are identical in the interior of the domain. However, close view on the inhomogeneous boundary $x=\text{0}$ as shown in Fig. 2 reveals that the exact solution ($N\to \mathrm{\infty }$) by the virtual-source conversion is discontinuous at $x=\text{0}$. With the inverse Laplace-Galerkin transform, Eq. (42) is almost equivalent to:

simultaneously with homogeneous boundary. Eq. (46) implies that the virtual source is actually impulsive on the homogeneous boundary. The virtual-source conversion realizes boundary inhomogeneity as delta sources combined by their derivatives.

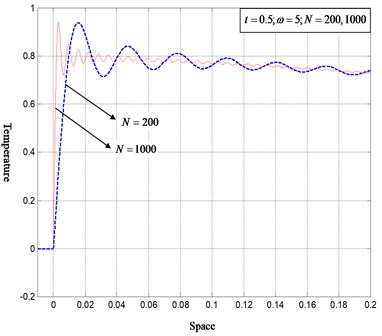
Figs. 3 and 4 show the virtual-source solution for time-varying environment: $f\left(t\right)=\mathrm{s}\mathrm{i}\mathrm{n}t$. At $t=\text{0.5}$, two order-reduced solutions according to $N=\text{200}$ and $N=\text{1000}$, respectively, are juxtaposed with each other. The convergence on the boundary appears, which implies that the solution will reach discontinuity at $x=\text{0}$ as $N\to \mathrm{\infty }$. This verifies again that the virtual-source conversion is of the strategy to zero the environment and simultaneously give impulsive sources on the homogeneous boundary, yielding almost the same solution.

Fig. 1Topological comparison of the virtual-source solution with the separation-of-variable solution under time-invariant environment

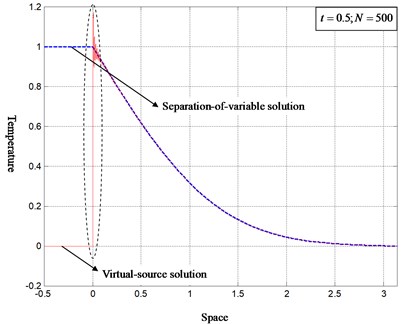
Fig. 2Close view on the inhomogeneous boundary of Fig. 1

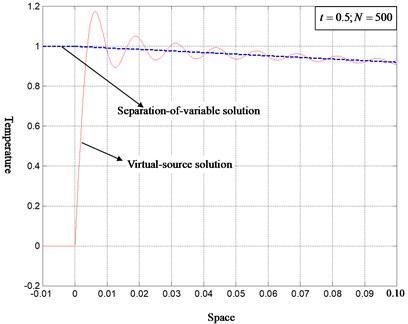
Fig. 3Topological convergence of the virtual-source solution under time-varying environment

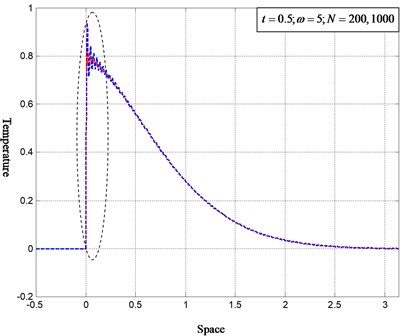
Fig. 4Close view on the inhomogeneous boundary of Fig. 3

6. Conclusion

For wave and heat-conduction dynamics, we can realize inhomogeneous boundary “conditions” as virtual-sources in conjunction with homogeneous boundary. The strategy such a virtual-source conversion is to zero the environment and simultaneously to introduce an impulsive source onto the homogeneous boundary, yielding the identical response in the interior of operation domain. Therein the boundary impulsive takes the form of Dirac delta function combined by its derivatives. In practice, this virtual-source conversion helps modal decomposition, real-time processing, computational intelligence, and system identification of distributed dynamics.