Abstract
In order to study the impact of human joint parameters on the pitching stability of a grenade launcher, a man-weapon interaction model of two rigid bodies with five degrees of freedom was developed according to the characteristics of shooting. By simulating with different values of human parameters individually, the pitching movement curves of the weapon were obtained. The equivalent parameters of the shooter have different influence on the firing stability of the weapon. The equivalent damping coefficients of the waist and the shoulder are critical to the design of the firearm mount, and the equivalent damping coefficient of the waist is the most important parameter.
1. Introduction
In addition to the factors of weapons, the shooter’s control factors can affect the stability of shooting. Early reports were concentrated on recoil analysis [1, 2] and man-weapon interaction force relationships of shoulder-fired weapons [3, 4]. The study of the simulation of the shooter and weapon was first appeared in the literature [3]. A three degrees of freedom mathematical model was developed that simulates the man and weapon as a coupled dynamical system. Through the sensitivity analysis of the parameters of the system and the experimental verification, the key parameters affecting the three degrees of freedom were obtained and the method of using the simplified model to study the system of man-gun system has been proved to be feasible. In the research of recoil analysis [1, 2], the recoil analysis to assess several recoil mitigating technologies applied to shoulder-fired weapons such as a grenade launcher or shotgun has been conducted, and three commercial recoil reducing devices were evaluated in the model to determine their specific effect on recoil motion, both on the weapon and on the soldier firing the weapon. In the research of the man-weapon interaction [3, 4], the model analysis and experimental study of the 56 type of assault rifle were carried out, and the change rule of the interaction of the man and weapon based on three shot burst and eight shot burst was obtained.
The purpose of this paper was to study the influence of human equivalent parameters on the pitching stability which is very useful to the shooting training of the soldiers and the design of intelligent firearm mount. According to a new type of grenade launcher firing test, a mathematical model for describing the firing system of the man and the weapon was established. Calculated with different values of the equivalent parameters of the shoulder and the waist, the weapon pitching curves were obtained. A detailed description of the system and the analysis performed along with the results follows below.
2. Man-weapon system modeling
As the human body is a nonhomogeneous composition of body segments with multiple degrees of freedom, the man-weapon system is a complex multi-body system [3-5]. Different system models had been developed for their respective research objectives in previous research [2-6]. In this paper, based on the movement characteristics of firing, the system was simplified to a mathematical model of two rigid bodies with five degrees of freedom as follows.
2.1. Simplifying assumption of system model
Compared with previous shooting experiments [3-5], the firing experiment of a new type of the grenade launcher appears the following movement characteristics of man-weapon system:
1) The weapon has recoil motion compared with the upper torso.
2) The weapon has pitching motion compared with the upper torso.
3) The shooter’s upper torso has pitching motion compared with the lower torso.
4) The shooter’s upper torso has yawing motion in the transverse plane.
5) There almost has no relative motion between the lower torso and ground.
According to above movement features, the man-weapon system model was simplified as:
1) In the dynamic equations, the breech pressure force of the grenade launcher was simplified to a pulse signal [3, 4].
2) The lower torso of the shooter was assumed to be fixed on the ground.
3) Relative to the lower torso, the pitching rotation and yawing rotation of upper torso were defined as two independent degrees of freedom. And the restrictive effect of the shooter's waist muscle on these degrees of freedom was simplified to the effect of two groups of equivalent springs and dampers.
4) Because of having the same movement in the firing process, the shooter’s arms and the weapon were simplified to an equivalent mass. Relative to the upper torso, this equivalent mass involves three independent degrees of freedom including the recoil motion, the pitching rotation and yawing rotation. The restriction effect of the shooter's shoulder muscle and arms on these degrees of freedom was simplified to the effect of three groups of equivalent springs and dampers. The shooting model was shown in Fig. 1.
Fig. 1Simplified model of standing shooting
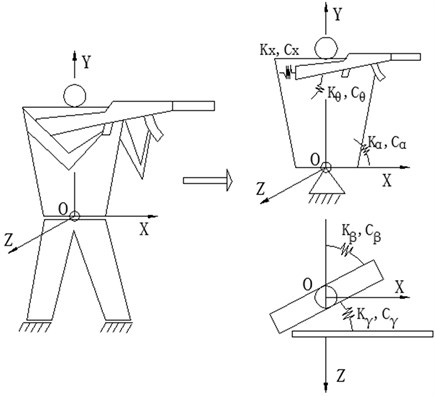
The coordinate system fixed with the earth was defined at the rotation center of the upper torso. The coefficients corresponding equivalent parameters were defined as follows:
, – equivalent elastic coefficient and damping coefficient of the shoulder joint in the recoil direction;
, – equivalent elastic coefficient and damping coefficient of the shoulder joint in the pitching direction;
, – equivalent elastic coefficient and damping coefficient of the shoulder joint in the yawing direction;
, – equivalent elastic coefficient and damping coefficient of the waist joint in the pitching direction;
, – equivalent elastic coefficient and damping coefficient of the waist joint in the pitching direction.
2.2. Dynamic equations of Man-weapon system
Corresponding to the five degrees of freedom about the simplified model, the generalized displacements of the system were:
– the generalized displacement of weapon recoil;
– the generalized displacement of the pitching of the weapon compared with the upper torso;
– the generalized displacement of the yawing of the weapon compared with the upper torso;
– the generalized displacement of the pitching of the upper torso compared with the lower torso;
– the generalized displacement of the yawing of the upper torso compared with the lower torso.
The centroid motion of the weapon and that of upper torso were converted into the inertial coordinate system , the system kinetic energy function, the system potential energy function and the dynamic differential equation were deduced by the Lagrange method as follows:
where: : The Lagrange function of system; : The dissipation function of system; , , , , : The generalized forces corresponding to the generalized displacements; and:
where: – the moment of inertia of the upper torso equivalent mass relative to axis; – the moment of inertia of the weapon equivalent mass relative to axis; – the moment of inertia of the upper torso equivalent mass relative to axis; – the moment of inertia of the weapon equivalent mass relative to axis; – the equivalent mass of the upper torso; – the equivalent mass of the shooter’s arms and the weapon; – the projection of distance between shoulder points and point in plane; – the projection of distance between shoulder points and point on axis; – the projection of distance between the centroid of weapon equivalent mass and shoulder points on axis; – the projection of distance between the acting point of gunpowder gas and the centroid of weapon equivalent mass on axis; – the projection of distance between the centroid of weapon equivalent mass and shoulder points on axis; – the projection of distance between the acting point of gunpowder gas and the centroid of weapon equivalent mass on axis; – the function of gunpowder gas force.
In the System dynamics equation, the values of human inertia parameters were calculated by statistical equations according to the shooter’s height and weight [4, 7]; the range of the equivalent elastic coefficient and damping coefficient were obtained by the identification experiment of model parameters [4, 5]; the function of gunpowder gas force was obtained by the pressure test experiment of the grenade launcher. The estimation of model parameters was shown in Table 1.
Table 1Estimation of model parameters
Parameters | Symbols and units | Value | Parameters | Symbols and units | Value |
Mass | / Kg | 6 | Damping coefficient | / N·S·M-1 | 300 |
Mass | / Kg | 30 | Damping coefficient | / N·M·S·Deg-1 | 0.5-4.5 |
Moment of inertia | / Kg·M2 | 1.0411 | Damping coefficient | / N·M·S·Deg-1 | 0.5-4.5 |
Moment of inertia | / Kg·M2 | 0.8185 | Damping coefficient | / N·M·S·Deg-1 | 0.5-4.5 |
Moment of inertia | / Kg·M2 | 0.3056 | Damping coefficient | / N·M·S·Deg-1 | 0.5-4.5 |
Moment of inertia | / Kg·M2 | 0.2738 | Geometric length | / M | 0.4 |
Elastic coefficient | / N·M-1 | 2000 | Geometric length | / M | 0.03 |
Elastic coefficient | / N·M·Deg-1 | 4-24 | Geometric length | / M | 0.02 |
Elastic coefficient | / N·M·Deg-1 | 1-5 | Geometric length | / M | 0.02 |
Elastic coefficient | / N·M·Deg-1 | 4-24 | |||
Elastic coefficient | / N·M·Deg-1 | 4-24 |
3. Influence of human equivalent parameters on pitching stability
As a principal influence factor for the firing stability of weapons [3, 8, 9], the pitching movement was discussed by calculating with different values of equivalent parameters (, , , , , , , ) individually. The results showed that the parameters, , , , , have no effect on pitch motion, while the parameters, , , , , have different influence on the pitching movement. The motion curves of the weapon were presented in Figs. 2-9 as follows.
Fig. 2Pitching angular displacement curves vs. Kθ
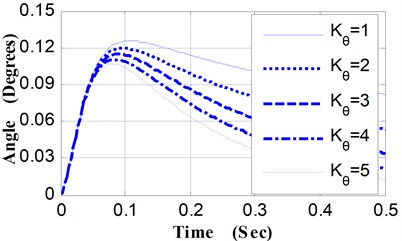
Fig. 3Pitching angular velocity curves vs. Kθ
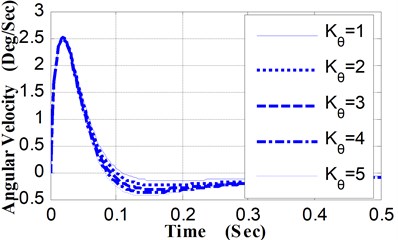
(1) Relative to different values of , the angular displacement curves and angular velocity curves of pitching movement were shown in Fig. 2 and Fig. 3. Along with the increase of , the peak value of the pitching angular displacement curves and the time corresponding to the maximum value decrease slightly. The pitching angular velocity curves, which are almost identical in the ascending phase, appear some difference only in the descent phase. Therefore, in the vicinity of the peak value of the pitching angular displacement curves, the slope of these curves appears corresponding difference.
The maximum pitching angle is 0.126°when is 1 (N·M·Deg-1), while the maximum pitching angle is 0.107° when is 5 (N·M·Deg-1), and the pitching angle of the weapon at the moment of projectile muzzle-leaving decrease from 0.0633° to 0.0618° (shown as Table 2). By the shooting deviation conversion, corresponding to the decrease of the pitching angle at the moment of projectile muzzle-leaving (0.0015°), the shooting deviation of the 100 m target is 0.26 centimeters.
Table 2Pitching angular displacement of weapon vs. Kθ
(N·M·Deg-1) | Max pitching angle of weapon (Deg) | Pitching angle of the weapon at the moment of projectile muzzle-leaving (Deg) |
1 | 0.126 | 0.0633 |
2 | 0.121 | 0.0629 |
3 | 0.115 | 0.0626 |
4 | 0.111 | 0.0622 |
5 | 0.107 | 0.0618 |
Fig. 4Pitching angular displacement curves vs. Cθ
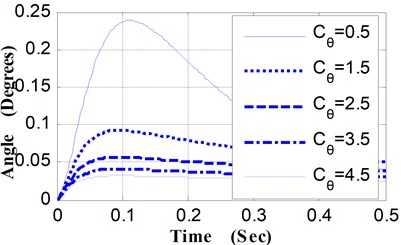
Fig. 5Pitching angular velocity curves vs. Cθ
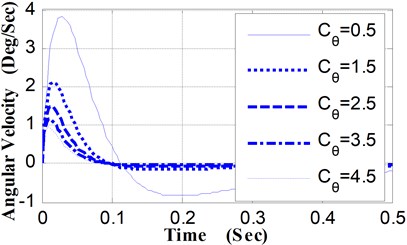
(2) Relative to different values of , the angular displacement curves and the angular velocity curves of pitching movement were shown in Fig. 4 and Fig. 5. Along with the increase of , the peak value of the pitching angular velocity curves decrease obviously, and the time corresponding to the maximum value decrease slightly. Accordingly, there are noticeable differences in the trend of the angular displacement curves.
The maximum pitching angle is 0.238°when is 0.5 (N·M·S·Deg-1), while the maximum pitching angle is 0.032° when is 4.5 (N·M·S·Deg-1), and the pitching angle of the weapon at the moment of projectile muzzle-leaving decrease from 0.0890° to 0.0224° (shown as Table 3). By the shooting deviation conversion, corresponding to the decrease of the pitching angle at the moment of projectile muzzle-leaving (0.0666°), the shooting deviation of the 100 m target is 11.62 centimeters.
Table 3Pitching angular displacement of weapon vs. Cθ
(N·M·S·Deg-1) | Max pitching angle of weapon (Deg) | Pitching angle of the weapon at the moment of projectile muzzle-leaving (Deg) |
0.5 | 0.238 | 0.0890 |
1.5 | 0.092 | 0.0532 |
2.5 | 0.057 | 0.0369 |
3.5 | 0.041 | 0.0279 |
4.5 | 0.032 | 0.0224 |
(3) Relative to different values of , the angular displacement curves and angular velocity curves of pitching movement were shown in Fig. 6 and Fig. 7. The variation characteristics of these curves are similar to that of curves presented in Fig. 2 and Fig. 3.
The maximum pitching angle is 1.92° when is 4 (N·M·Deg-1), while the maximum pitching angle is 1.41° when is 24 (N·M·Deg-1), and the pitching angle of the weapon at the moment of projectile muzzle-leaving decrease from 0.814° to 0.775° (shown as Table 4). By the shooting deviation conversion, corresponding to the decrease of the pitching angle at the moment of projectile muzzle-leaving (0.039°), the shooting deviation of the 100 m target is 6.81 centimeters.
(4) Relative to different values of , the angular displacement curves and the angular velocity curves of pitching movement were shown in Fig. 8 and Fig. 9. The variation characteristics of these curves are similar to that of curves presented in Fig. 4 and Fig. 5.
The maximum pitching angle is 6.96° when is 0.5 (N·M·S·Deg-1), while the maximum pitching angle is 1.33° when is 4.5 (N·M·S·Deg-1), and the pitching angle of the weapon at the moment of projectile muzzle-leaving decrease from 1.53° to 0.63° (shown as Table 5). By the shooting deviation conversion, corresponding to the decrease of the pitching angle at the moment of projectile muzzle-leaving (0.9°), the shooting deviation of the 100 m target is 157.1 centimeters.
Fig. 6Pitching angular displacement curves vs. Kα
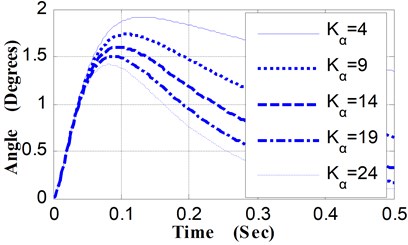
Fig. 7Pitching angular velocity curves vs. Kα
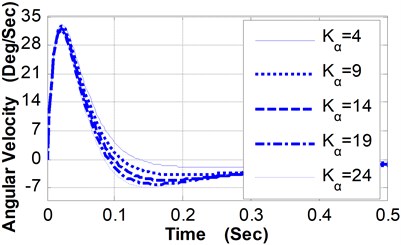
Table 4Pitching angular displacement of weapon vs. Kα
Kα (N·M·Deg-1) | Max pitching angle of weapon (Deg) | Pitching angle of the weapon at the moment of projectile muzzle-leaving (Deg) |
4 | 1.92 | 0.814 |
9 | 1.73 | 0.804 |
14 | 1.60 | 0.794 |
19 | 1.50 | 0.785 |
24 | 1.41 | 0.775 |
Fig. 8Pitching angular displacement curves vs. Cα
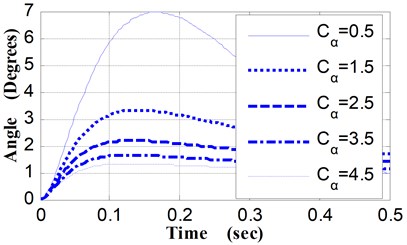
Fig. 9Pitching angular velocity curves vs. Cα
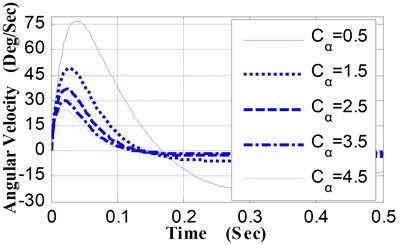
Table 5Pitching angular displacement of weapon vs. Cα
(N·M·S·Deg-1) | Max pitching angle of weapon (Deg) | Pitching angle of the weapon at the moment of projectile muzzle-leaving (Deg) |
0.5 | 6.96 | 1.53 |
1.5 | 3.32 | 1.13 |
2.5 | 2.19 | 0.89 |
3.5 | 1.65 | 0.74 |
4.5 | 1.33 | 0.63 |
As stated above, the effects of the equivalent elastic coefficients and the equivalent damping coefficient on the pitching movement of weapons were different significantly:
1) With the increase of the equivalent elastic coefficients, the pitching angle of the weapon at the moment of projectile muzzle-leaving decreases a little, and the maximum value of the pitching angular velocity curves in the positive direction has a very small decrease, however, the maximum value of these curves in the opposite direction increases slightly.
2) With the increase of the equivalent damping coefficients, the pitching angle of the weapon at the moment of projectile muzzle-leaving decreases obviously, and the maximum value of the pitching angular velocity curves both in the positive direction and the opposite direction decreases evidently.
3) In the same interval, the effects of on the pitching angular displacement curves and pitching angular velocity curves are more obvious than that of .
The authors declare that there is no conflict of interests regarding the publication of this article.
4. Conclusions
Based on the dynamic model of man-weapon system consisted of two rigid bodies with five degrees of freedom, the effect of human equivalent parameters on the pitching stability of the grenade launcher was discussed. The simulation results showed that the fundamental parameters for the stability of pitching movement were , , and , and the conclusions were as follows:
1) To increase the value of or individually is beneficial to the stability of the pitching angular displacement, but it is not conducive to the stability of the pitching angular velocity. And the influence of these parameters on pitching movement is small.
2) To increase the value of or individually is very useful to the stability of pitching movement. Moreover, is the most critical parameter and the range of it should be defined strictly.
References
-
Philip D. Benzkofer Dynamic Analysis of Shoulder-Fired Weapons. AD: P009073, 1993.
-
Wang Chang-geng, Xu Wan-he, Xu Cheng Research on the influence of different automatic action of gun on its recoil effect in man-gun system. ACTA Armamentarii, Vol. 35, Issue 5, 2014, p. 741-747.
-
Thomas D. Hutchings, Albert E. Rahe Study of Man-Weapon Reaction Forces Application to the Fabrication of a Standard Rife Firing Fixture. AD: A034523, 1975.
-
Li Yong-xin Model and Experimental Study of Human Interaction Gun. Nanjing University of Technology and Engineering, 1993.
-
Bao Jian-dong, Wang Chang-ming, He Yun-feng Foundation of mart gun model and simulation analysis. ACTA Armamentarii, Vol. 30, Issue 5, 2009, p. 513-517.
-
Gong Peng-han, Zhou Ke-dong, Kang Xiao-yong, et al. Simulation of launch dynamics of a rifle. Journal of Ballistics, Vol. 26, Issue 1, 2014, p. 94-97.
-
Zheng Xiu-yuan Modern Sports Biomechanics. Defense Industry Press, Beijing, 2002.
-
Chen Jin-xi, Wang Rui-lin, Wu Hai-feng Dynamic characteristics analysis for a new type gun tripod. Journal of Vibration and Shock, Vol. 31, Issue 8, 2012, p. 121-123.
-
Zhang Ben-jun, Wang Rui-lin, Li Yong-jian, et al. Structural optimization for a machine-gun mount based on BP neural network and genetic algorithm. Journal of Vibration and Shock, Vol. 30, Issue 1, 2011, p. 142-144.
About this article
The authors wish to express their deep appreciation to Mr. Liu bing, Mr. Gong Peng-han and to the test crew at weapon shooting laboratory of Nanjing University of Science and Technology, for their contribution in the test experiment and data reduction efforts, in each of the tests conducted in support of this study.
